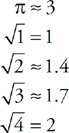Chapter 13
Geometry
The geometry tested on the GMAT is but a small fraction of the geometry you probably studied during high school. In this chapter, we cover the geometry the test-makers actually test: angles, triangles, circles, quadrilaterals, volume, surface area, and coordinate geometry.
CRAZY ANSWERS
Eliminating choices that don’t make sense has already proven to be a valuable technique on arithmetic and algebra questions. On geometry questions you can develop this technique into an art form. The reason for this is that many geometry problems come complete with a diagram drawn to scale.
Crazy Answers on Easy Questions
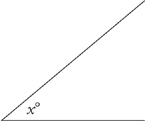
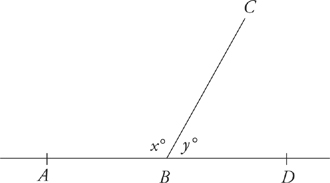
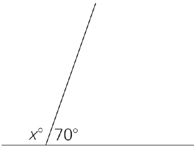
How big is angle x?
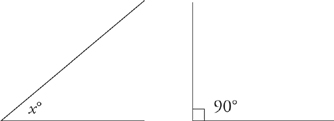
Obviously you don’t know exactly how big this angle is, but it would be easy to compare it with an angle whose measure you do know exactly. Let’s compare it with a 90-degree angle:
Angle x is less than 90 degrees. How much less? It looks as though it’s about half of a 90-degree angle, or 45 degrees. Now look at the following problem that asks about the same angle, x.
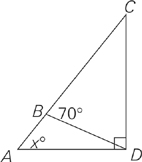
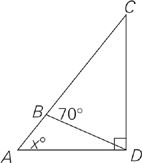
In the figure above, if BC = CD and angle ADC = 90 degrees, then what is the value of x?
We’ve already decided that angle x is less than 90 degrees, which means that the last answer choice (what we call choice E) can be eliminated. How much less is it? Well, we estimated before that it was about half, which rules out answer choices C and D as well.
There is another way to eliminate choices C and D. We can compare angle x with the other marked angle in the problem—angle DBC. If the answer to this problem is choice C, then angle x should look like angle DBC. Does it? No. Angle x looks a little bit smaller than angle DBC, which means that both choices C and D can be eliminated.
Eliminating crazy answers will prevent you from making careless mistakes on easy problems.
Crazy Answers on Difficult Questions
If it’s important to cross off crazy answer choices on easy questions, it’s even more important to eliminate crazy answer choices when you’re tackling an average or difficult geometry problem. On these problems, you may not know how to find the answer geometrically, and even if you do, you could still fall victim to one of the traps the test writers have placed in your path. Take a look at the following difficult geometry problem:
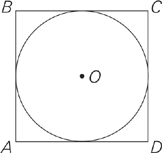
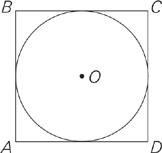
In the figure above, the circle with center O, is inscribed inside square ABCD as shown. What is the ratio of the area of circle O to the area of square ABCD?
But before you start guessing at random, let’s see whether you can eliminate any of the answer choices just by looking at the diagram and using some common sense.
The problem asks you for the ratio of the area of the circle to the area of the square. Just by looking at the diagram, you can tell that the circle is smaller than the square. The correct answer to this question has to be the ratio of a smaller number to a bigger number. Let’s look at the answer choices.
In choice A, the ratio is π over 2. An approximate value of π is 3, so this really reads  .
.
Is this the ratio of a smaller number to a bigger number? Just the opposite. Therefore choice A is a crazy answer. Eliminate it.
In choice B, the ratio is 4 over π. This really reads  .
.
Is this the ratio of a smaller number to a bigger number? No. Choice B is a crazy answer. Eliminate it.
In choice C, the ratio is π over 3. This really reads  .
.
Is this the ratio of a smaller number to a bigger number? No. Choice C is a crazy answer. Eliminate it.
Answer choices D and E both contain ratios of smaller numbers to bigger numbers, so they’re both still possibilities. However, we’ve eliminated three of the answer choices without doing any math. If you know how to solve the problem geometrically, then proceed. If not, guess and move on. (By the way, we will show you how to solve this problem using geometry later in the chapter.)
The Basic Tools
In eliminating crazy answers, it helps to have the following approximations
memorized.
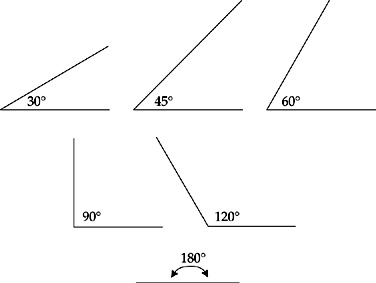
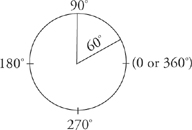
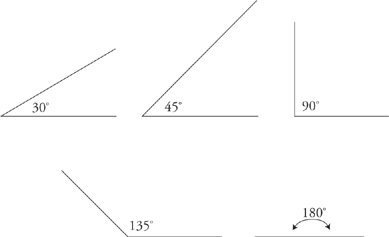
It’s also useful to have a feel for the way certain common angles look:
Getting More Precise
When a geometry problem contains a diagram that’s drawn to scale, you can get even more precise in eliminating wrong answer choices.
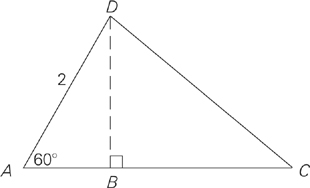
In the figure above, if a line segment connecting points B and D is perpendicular to AC and the area of triangle ADC is  , then BC = ?
, then BC = ?
Here’s How to Crack It
Practice measuring the diagram with your pen or pencil. If you measure carefully, you’ll notice that the distance between A and D is the same as the distance between B and C—exactly 2. Let’s look at the answer choices. Because you memorized the values we told you to memorize earlier, you know that answer choice A is equal to 1.4. Eliminate it. Answer choice B is equal to 1.7. This is close enough for us to hold
on to it while we look at the other choices. Choice C is exactly what we’re looking for—2. Choice D is 3 times 1.7, which equals 5.1. This is much too large. Choice E is even larger. Eliminate D and E. We’re down to choices B and C. The correct answer is choice C.
Two Important Notes
- Diagrams in questions using the problem-solving format may be drawn to scale (unless otherwise indicated), but they are not all drawn to the same scale.
- Diagrams marked “not drawn to scale” cannot be measured. In fact, the drawings in these problems are often purposely misleading to the eye.
What Should I Do if There Is No Diagram?
Draw one. It’s always difficult to imagine a geometry problem in your head. The first thing you should do with any geometry problem that doesn’t have a diagram is sketch it out in your scratch booklet. And when you draw the diagram, try to draw it to scale. That way, you’ll be in a position to estimate.
What Should I Do if the Diagram Is Not Drawn to Scale?
The same thing you would do if there were no diagram at all—draw it yourself. Draw it as accurately as possible so you’ll be able to see what a realistic answer should be.
Basic Principles: Fundamentals of GMAT Geometry
The techniques outlined above will enable you to eliminate many incorrect choices on geometry problems. In some cases, you’ll be able to eliminate every choice but one. However, there will be some geometry problems in which you will need geometry. Fortunately, GMAC chooses to test only a small number of concepts.
- degrees and angles
- triangles
- circles
- rectangles, squares, and other four-sided objects
- solids and volume
- coordinate geometry
DEGREES AND ANGLES
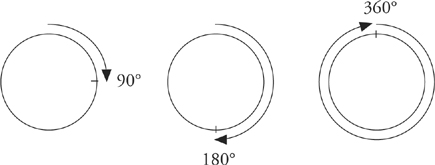
There are 360 degrees in a circle. No matter how large or small a circle is, it still has precisely 360 degrees. If you drew a circle on the ground and then walked a quarter of the distance around it, you would have traveled 90 degrees of that circle. If you walked halfway around the circle, you would have traveled 180 degrees of it.
An angle is formed when two line segments extend from a common point. If you think of that point as the center of a circle, the measure of the angle is the number of degrees enclosed by the lines when they pass through the edge of the circle.
A line is just a 180-degree angle.
 is the symbol for a line. A line can be referred to as
is the symbol for a line. A line can be referred to as  or by naming two points on that line. For example, in the diagram below, both points A and B are on the line
or by naming two points on that line. For example, in the diagram below, both points A and B are on the line  . This line could also be called line AB. Also, the part of the line that is between points A and B is called a line segment. A and B are the end points of the line segment.
. This line could also be called line AB. Also, the part of the line that is between points A and B is called a line segment. A and B are the end points of the line segment.
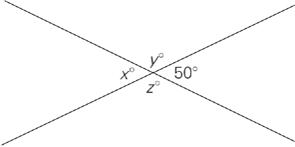
If a line is intersected by another line, as in the diagram below, angle x and angle y add up to one straight line, or 180 degrees. So, for example, if you know that angle x equals 120 degrees, you can find the measure of angle y by subtracting 120 degrees from 180 degrees. Thus angle y would equal 60 degrees.
Note that in the diagram above, angle x could also be called angle ABC, with B being the point in the middle.
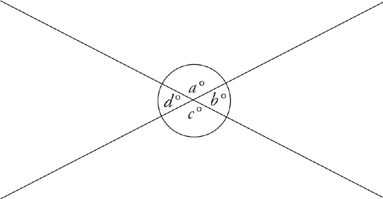
The four angles add up to 360 degrees (remember the circle).
a° + b° + c° + d° = 360 degrees. Angle a + angle b, because they form a straight line, are equal to 180 degrees. Angle b + angle c also form a straight line, as do c + d and d + a. Angles that are opposite each other are called vertical angles and have the same number of degrees. For example, in the
diagram above, angle a is equal to angle c. Angle d is equal to angle b.
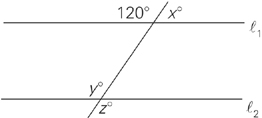
Two lines in the same plane are said to be parallel if they extend infinitely in both directions without intersecting. The symbol for parallel is  .
.
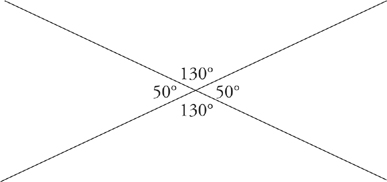
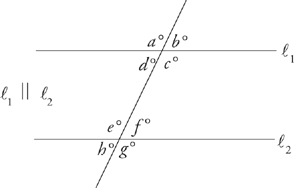
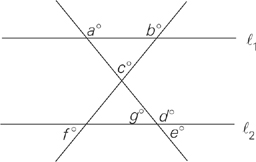
When two parallel lines are intersected by a third line, there appear to be eight different angle measurements, but there are really only two.
There is a big one (greater than 90°) and a little one (less than 90°). Angle a (a big one) is equal to angles c, e, and g. Angle b (a little one) is equal to angles d, f, and h.
Angles a, b, c, and d each equal 90 degrees. The little box at the intersection of the two lines is the symbol for a right angle.
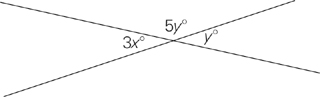
In the figure above, what is the value of x?
Here’s How to Crack It
On a GMAT geometry problem, you may not know exactly how to solve at first glance, but there is almost always something you can do to get started. Did you notice that 5y and y together make up a straight line? In other words, 6y = 180 degrees. Noticing this is the key to solving the problem. If 6y = 180 degrees, then y equals 30 degrees. You might be tempted to pick choice D, but remember—we aren’t looking
for the value of y, we’re looking for the value of x. Opposite angles formed by two straight lines are always equal—so y is equal to 3x. Therefore, 3x also equals 30 degrees, and the correct answer to this problem is choice A, 10 degrees.

Remember that all problem solving diagrams on the GMAT are drawn to scale unless labeled otherwise. So be sure to take a step back and think about which answer choices are even within the realm of possibility. Looking at the angle labeled 3x, would you say it is greater than 90 degrees or less than 90 degrees? If you said less than 90 degrees, you are doing just fine. So if 3x is less than 90, then x must be smaller than 30 degrees.
Eliminate choices D and E.
DRILL 6 (Angles and Lengths)
In the following figures, find numbers for all the variables. The answers to these problems can be found in Part VI.
4. If a driver has traveled 270 degrees around a circular race track, what fractional part of the track has he driven?
A real GMAT angle problem might look like this:
Note: Figure not drawn to scale.
5. In the figure above, if  1
1

 2, then which of the following angles must be equivalent?
2, then which of the following angles must be equivalent?
 |
a and b |
 |
g and f |
 |
d and e |
 |
a and d |
 |
f and d |
You might see a very straightforward data sufficiency problem like this on the GMAT:
6. What is the degree measure of angle x?
(1) Angle y = 40 degrees.
(2) Angle x and angle y add up to a straight line.
TRIANGLES
A triangle is a three-sided figure that contains three interior angles. The sum of the degree measures of the three angles in a triangle is 180 degrees. Several kinds of triangles appear on the GMAT:
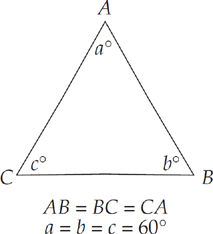
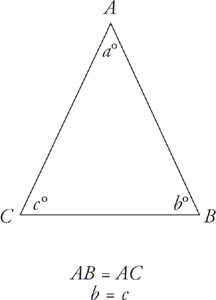
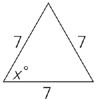
An equilateral triangle has three sides that are equal in length. Because the angles opposite equal sides are also equal, all three angles in an equilateral triangle are equal.
A right
triangle has one interior angle that is equal to 90 degrees. The longest side of a right triangle (the one opposite the 90-degree angle) is called the hypotenuse.
Everything Else You Need to Know About Triangles
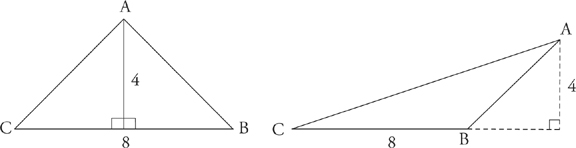
1. The sides of a triangle are in the same proportion as its angles. For example, in the triangle below, which is the longest side?
The longest side is opposite the largest angle. The longest side in the triangle above is AB. The next longest side would be AC.
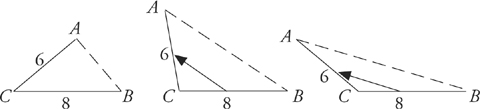
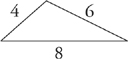
2. One side of a triangle can never be longer than the sum of the lengths of the other two sides of the triangle, or less than their difference. Why? Look at the diagrams below:
At the point where angle ACB = 180 degrees, this figure ceases to be a triangle. Angle ACB becomes 180 degrees when side AB equals the sum of the other two sides, in this case 6 + 8. Side AB can never quite reach 14.
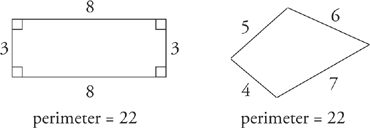
3. The perimeter of a triangle is the sum of the lengths of the three sides.
perimeter = 18
4. The area of a triangle is equal to 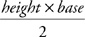 . By definition, the base and height must be perpendicular to each other.
. By definition, the base and height must be perpendicular to each other.
In both of the above triangles, the area = 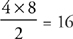 .
.
In a right triangle, the height also happens to be one of the sides of the triangle:
5. Don’t expect triangles to be right side up:
This is an isosceles triangle.
The area of this triangle is 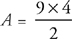 , or 18.
, or 18.
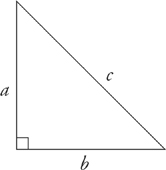
6. In a right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides. In the triangle below:
a2 + b2 = c2
This is called the Pythagorean theorem. The test writers love to test this theorem, but usually you won’t actually have to make use of it if you’ve memorized a few of the most common right-triangle proportions.
There are two other kinds of right triangles that GMAC loves to test. These are a little complicated to remember, but they come up so often that they’re worth memorizing.
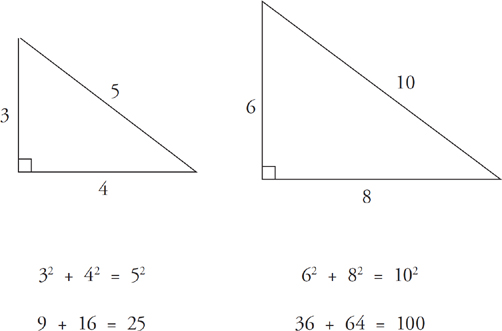
Pythagorean Triples
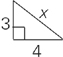
The right triangle in the ratio 3 : 4 : 5 is the most common Pythagorean triple, but it’s not the only one that shows up on the GMAT:
3 : 4 : 5
5 : 12 : 13
7 : 24 : 25
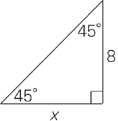
7. A right isosceles triangle always has proportions in the ratio
side: side: side 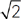 .
.
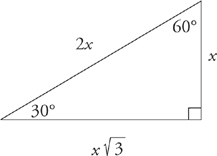
8. The second special right triangle is called the 30-60-90 right triangle. The ratio between the lengths of the sides in a 30-60-90 triangle is constant. If you know the length of any of the sides, you can find the lengths of the others. The ratio of the sides is always x:x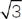 :2x.
:2x.
That is, if the shortest side is length x, then the hypotenuse is 2x, and the remaining side is x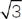 .
.
Try this problem:
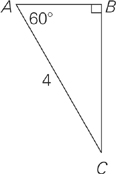
In ΔABC shown above, if ΔCAB equals 30°, then what is the area of the triangle?
Here’s How to Crack It
As with all geometry problems, even if you aren’t exactly sure how to solve, there may be something you can do to get started—always half the battle. In this case, since we know thatis a right triangle, and the problem tells you thatequals 30, do we know the value of? We do: it must be 60° (since there are a total of 180 degrees in a triangle). Because this is a 30-60-90 triangle (which always has sides in proportion of x, 2x,
and), and the diagram gives us all the measurement of one of those sides, we actually know the measurement of all sides: 2, 2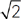 , and 4. To find the area, we simply multiply the base times the height and divide by 2:
, and 4. To find the area, we simply multiply the base times the height and divide by 2:
DRILL 7 (Triangles)
Find the value of the variables in the following problems. The answers can be found in Part VI.
4. What value must x be less than in the triangle below? What value must x be greater than?
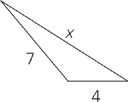
5. In the square ABCD below, what is the length of line segment AC?
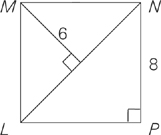
6. In the triangle below, what is the length of the line segment BC?
A real GMAT triangle problem might look like this:
7. In the diagram below, if the area of triangle LNP is 32, then what is the area of triangle LMN?
Note: Figure not drawn to scale.
You might see a data sufficiency problem like this on the GMAT:
8. What is the value of x in triangle ABC shown above?
(1) Angle y = 80 degrees.
(2) AB = BC
CIRCLES
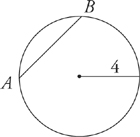
A line on the circumference of a circle is called a chord. The distance from the center of the circle to any point on the circle is called the radius. The distance from one point on the circle through the center of the circle to another point on the circle is called the diameter. The diameter is equal to twice the radius.
radius = 4
diameter = 8
AB is a chord.
The circumference (the length of the entire outer edge of the circle) = 2πr or πd.
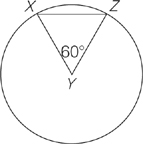
If the circle above has center y and area 4π, then what is the perimeter of triangle XYZ?
Here’s How to Crack It
As always, the solution to this problem will probably only become apparent once you’ve started doing the problem. The only apparent information you’ve been given: the area of the circle, 4π. Since the formula for the area of a circle is πr2, set that equal to 4π. Can you figure out what r equals? That’s right, 2. And since both sides XY and YZ are radii of the
circle, they must both equal 2. To find the perimeter of the triangle, the last thing we need to do is find the length of XZ. You might not think that you know what XZ equals, but the diagram tells us that angle XYZ equals 60 degrees. Since we know sides xy and yz are equal, that means that this triangle must be equilateral: all three sides have the same length, 2. Therefore, the perimeter of triangle XYZ is 6, and the answer is
choice D.
DRILL 8 (Circles)
Answer the following questions. The answers can be found in Part VI.
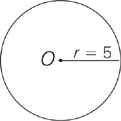
1. In the circle below with center O, what is the area of the circle? What is the circumference?
2. If the area of a circle is 36π, what is the circumference?
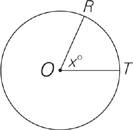
3. In the circle below with center O, if the arc RT is equal to  of the circumference, what is the value of x?
of the circumference, what is the value of x?
A real GMAT circle problem might look like this:
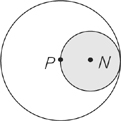
4. In the figure above, P is the center of the larger circle, and N is the center of the smaller, shaded circle. If the radius of the smaller circle is 5, what is the area of the unshaded region?
You might see a data sufficiency problem like this on the GMAT:
5. What is the area of circle P?
(1) The diameter of circle Q is 6.
(2) The radius of circle Q is twice the radius of circle P.
RECTANGLES, SQUARES, AND OTHER FOUR-SIDED OBJECTS
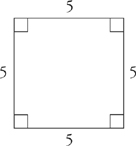
A four-sided figure is called a quadrilateral. The perimeter of any four-sided object is the sum of the lengths of its sides. A rectangle is a quadrilateral whose four interior angles are each equal to 90 degrees. Opposite sides of a rectangle are always equal.
The area of a rectangle is length × width. The area of the rectangle above is therefore 3 × 8, or 24.
perimeter = 4 × 5 = 20
area = 5 × 5 = 25
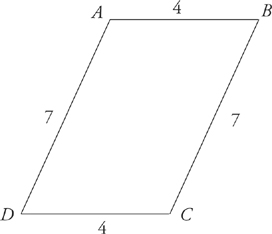
A parallelogram is a quadrilateral in which the two pairs of opposite sides are parallel to each other and equal to each other, and in which opposite angles are equal to each other. A rectangle is obviously a parallelogram, but so is a figure like this:
Angle ADC = angle ABC, and angle DAB = angle DCB.
The area of parallelogram ABCD = 8 × 2 = 16. (If you are having trouble picturing this, imagine cutting off the triangular region ADE and sticking it onto the other end of the figure. What you get is a rectangle with dimensions 8 by 2.)
SOLIDS, VOLUME, AND SURFACE AREA
The GMAT will occasionally ask you to find the volume or surface area of a three-dimensional object.
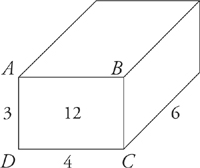
The volume of the rectangular solid above is equal to the area of the rectangle ABCD times the depth of the solid—in this case, 12 × 6, or 72. Another way to think of it is length × width × depth = 3 × 4 × 6, or 72.
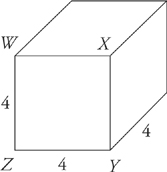
The volume of a cube is equal to the area of the square WXYZ times the depth of the cube, or again, length × width × depth. In the case of a cube, the length, width, and depth are all the same, so the volume of a cube is always the length of any side, cubed. The volume of this cube is 4 × 4 × 4, or 64.
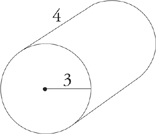
The volume of a cylinder is equal to the area of the circular base times the depth. The area of this circle is 9π. Thus the volume of the cylinder is 36π.
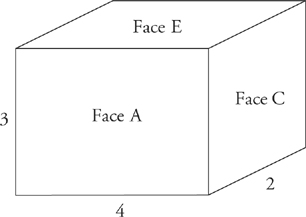
| Face A: |
3 × 4 = |
12 |
Face B:
(opposite Face A) |
3 × 4 = |
12 |
| Face C: |
3 × 2 = |
6 |
Face D:
(opposite Face C) |
3 × 2 = |
6 |
| Face E: |
4 × 2 = |
8 |
Face F:
(opposite Face E) |
4 × 2 = |
8 |
| Surface Area: |
= |
52 |
COORDINATE GEOMETRY
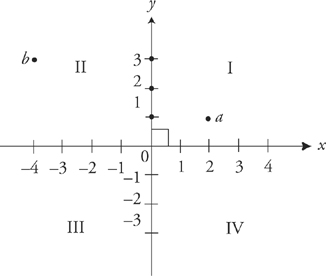
A coordinate plane, like the one above, lets you plot out lines and objects in two-dimensions. If you played the game Battleship as a child, this should feel very familiar—even if you don’t remember learning about it in high school. The horizontal line is called the x-axis. The vertical line is called the y-axis. The axes divide the plane into four quadrants as shown above.
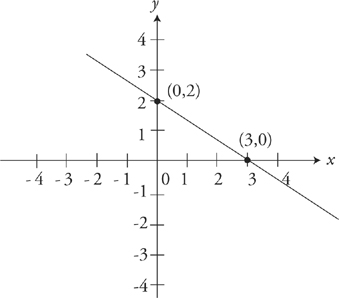
For example, the y-intercept of the line shown above is 2 (that’s where it crosses the y-axis). You can find the slope of any line if you know any two points on that line:
For example, the slope of the line above is
So the equation of this line can be written as 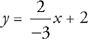 .
.
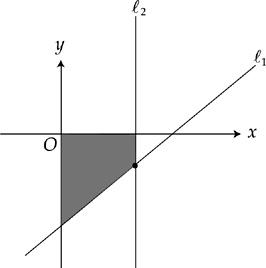
In the coordinate plane above, if the equation of  1 is y = x − 3 and the equation of
1 is y = x − 3 and the equation of  2 is x = 2, then what is the area of the shaded region?
2 is x = 2, then what is the area of the shaded region?
(A) 3
(B) 4
(C) 3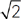
(D) 4.5
(E) 5
Here’s How to Crack It
First, draw your own coordinate axes. The equation for  1 is y = x − 3, which means that the y-intercept is −3 and the slope is 1. That means the bottommost point of the large triangle is point (0, −3), and the rightmost point of the large triangle is (3, 0). What we have here is an
upside-down right triangle with base 3 and height 3. The area of this entire triangle is
1 is y = x − 3, which means that the y-intercept is −3 and the slope is 1. That means the bottommost point of the large triangle is point (0, −3), and the rightmost point of the large triangle is (3, 0). What we have here is an
upside-down right triangle with base 3 and height 3. The area of this entire triangle is 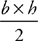 or
or  , which is choice D, but we aren’t done yet. Now we have to find the area of the small triangle, and subtract it from the large triangle. What remains will be the shaded region.
, which is choice D, but we aren’t done yet. Now we have to find the area of the small triangle, and subtract it from the large triangle. What remains will be the shaded region.
GMAT GEOMETRY: ADVANCED PRINCIPLES
All geometry problems (even easy ones) involve more than one step. Remember the first problem we looked at in this chapter?
In the figure above, if BC = CD and angle ADC = 90 degrees, then what is the value of x?
Here’s How to Crack It
Just by looking at the figure, we were able to eliminate answer choices C, D, and E. Now let’s solve the problem using geometry. The figure includes two—actually three—different triangles: ABD, BCD, and ACD. The test writers want even this easy problem to be a little challenging; there must be more than one step involved. To find angle x, which is part of triangles ABD and ACD, we must first work on
triangle BCD.
Walking and Chewing Gum at the Same Time
Most GMAT geometry problems involve more than one geometric concept. A problem might require you to use both the properties of a triangle and the properties of a rectangle, or you might need to know the formula for the volume of a cube in order to find the dimensions of a cube’s surface area. The difficult geometry problems do not test more complicated concepts—they just pile up easier concepts.
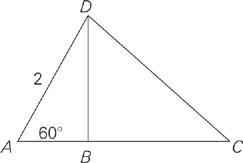
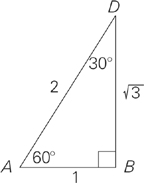
In the figure above, if a line segment connecting points B and D is perpendicular to AC, and the area of triangle ADC is 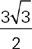 , then BC =
, then BC =
Here’s How to Crack It
We already got an approximate answer to this question by measuring; now let’s solve it using geometry. If we draw in the line BD (which is perpendicular to line AC), we form a 30-60-90 triangle on the left side of the diagram (triangle ADB). The hypotenuse of this triangle is 2. Using the rules we’ve learned about 30-60-90 triangles, we can conclude that the measurements of triangle ADB are as follows:
Thus BD = 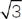 . At first you might think we’re no closer to the solution, but don’t despair. Just look for somewhere else to start. The problem tells us that the area of triangle ADC is
. At first you might think we’re no closer to the solution, but don’t despair. Just look for somewhere else to start. The problem tells us that the area of triangle ADC is 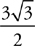 . The area of a triangle is
. The area of a triangle is 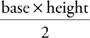 . BD is the height. Let’s find out what the base is. In other words,
. BD is the height. Let’s find out what the base is. In other words, 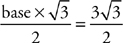 , so the base equals 3. We know from the 30-60-90 triangle that AB = 1. What is BC? 2. The answer is choice C.
, so the base equals 3. We know from the 30-60-90 triangle that AB = 1. What is BC? 2. The answer is choice C.
Plugging In on Geometry?
In the figure above, circle O is inscribed inside square ABCD as shown. What is the ratio of the area of circle O to the area of square ABCD?
Here’s How to Crack It
We already saw this problem in the first half of the chapter when we discussed eliminating crazy answers. As you recall, we were able to eliminate answer choices A, B, and C because we determined that the correct answer had to be the ratio of a smaller number to a bigger number.
The answer is choice D.
Summary
- While the geometry found on the GMAT is rudimentary, you will have to memorize all of the formulas that you’ll need because they are not provided on the test.
- Always study any problem drawn to scale very closely in order to eliminate crazy answer choices.
- You must know the following approximate values: π ≈ 3,
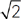 ≈ 1.4, and
≈ 1.4, and 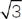 ≈ 1.7.
≈ 1.7.
- You must be familiar with the size of certain common angles:
- You can estimate problem solving diagrams drawn to scale very precisely by using the marker that comes with your scratch booklet.
- When no diagram is provided, draw your own, and make it to scale.
- When the diagram is not drawn to scale, redraw it.
- Degrees and angles:
- A circle contains 360 degrees.
- When you think about angles, remember circles.
- A line is a 180-degree angle.
- When two lines intersect, four angles are formed, but in reality there are only two pairs of identical angles.
- When two parallel lines are cut by a third line, eight angles are formed, but in reality there are only two sets of identical angles: a set of big ones and a set of little ones.
- Triangles:
- Every triangle contains 180 degrees.
- An equilateral triangle has three equal sides and three equal angles, each of which measures 60 degrees.
- An isosceles triangle has two equal sides, and the angles opposite those sides are also equal.
- A right triangle contains one 90-degree angle.
- The perimeter of a triangle is the sum of the lengths of its sides.
- The area of a triangle is
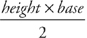 .
.
- In a right triangle, the Pythagorean theorem states that the square of the hypotenuse equals the sum of the squares of the other two sides, or a2 + b2 = c2.
- Some common right triangles are 3-4-5 triangles and multiples of 3-4-5 triangles, 5-12-13 triangles, and 7-24-25 triangles.
- Two other triangles that often appear on the GMAT are the right isosceles triangle and the 30-60-90 triangle. Memorize the formulas for these two triangles.
- The longest side of a triangle is opposite the largest angle; the shortest side is opposite the smallest angle.
- One side of a triangle can never be as large as the sum of the two remaining sides, nor can it ever be as small as the difference of the two remaining sides.
- Circles:
- The circumference of a circle is 2πr or πd, where r is the radius of the circle and d is the diameter.
- The area of a circle is πr2, where r is the radius of the circle.
- Rectangles, squares, and other four-sided objects:
- Any four-sided object is called a quadri-lateral.
- The perimeter of a quadrilateral is the sum of the lengths of the four sides.
- The area of a rectangle, or of a square, is equal to length × width.
- The area of a parallelogram is equal to height × base.
- Solids and volume:
- The volume of most objects is equal to their two-dimensional area × their depth.
- The volume of a rectangular solid is equal to length × width × depth.
- The volume of a cylinder is equal to the area of the circular base × depth.
- GMAT geometry problems always involve more than one step, and difficult GMAT geometry problems may layer several concepts. Don’t be intimidated if you don’t see the entire process that’s necessary to solve the problem. Start somewhere. You’ll be amazed at how often you arrive at the answer.