17.1 Introduction
In this chapter we consider bilevel optimization models with uncertain parameters. Such models can be classified based on the chronology of decision and observation as well as the nature of the uncertainty involved. A bilevel stochastic program arises, if the uncertain parameter is realization of some random vector with known distribution, that can only be observed once the leader has submitted their decision. In contrast, the follower decides under complete information.
If upper and lower level objectives coincide, the bilevel stochastic program collapses to a classical stochastic optimization problem with recourse (cf. [1, Chap. 2]). Relations to other mathematical programming problems are explored in the seminal work [2] that also established the existence of solutions, Lipschitzian properties and directional differentiability of a risk-neutral formulation of a bilevel stochastic nonlinear model. Moreover, gradient descent and penalization methods were investigated to tackle discretely distributed stochastic mathematical programs with equilibrium constraints (SMPECs).
Reference [3] studies an application to topology optimization problems in structural mechanics. Many other applications are motivated by network related problems that inherit a natural order of successive decision making under uncertainty. Notable examples arise in telecommunications (cf. [4]), grid-based (energy) markets (cf. [5–8]) or transportation science (cf. [9, 10]). An extensive survey on bilevel stochastic programming literature is provided in [11, Chap. 1.4].
In two-stage stochastic bilevel programming leader and follower take two decisions: The decision on the respective first-stage variables is made in a here-and-now fashion, i.e. without knowledge of the realization of the random parameter. In contrast, the respective second-stage decisions are made in a wait-and-see manner, i.e. after observing the parameter (cf. [12]).
This chapter is organized as follows: In Sects. 17.2.1–17.2.5, we outline structural properties, existence and optimality conditions as well as stability results for bilevel stochastic linear problems while paying special attention to the modelling of risk-aversion via coherent or convex risk measures or stochastic dominance constraints. Sections 17.2.6 and 17.2.7 are devoted to the algorithmic treatment of bilevel stochastic linear problems, where the underlying distribution is finite discrete . An application of two-stage stochastic bilevel programming in the context of network pricing is discussed in Sect. 17.3. The chapter concludes with an overview of potential challenges for future research.
17.2 Bilevel Stochastic Linear Optimization
While the analysis in this section is confined to the bilevel stochastic linear problems with random right-hand side , the concepts and underlying principles can be easily transferred to stochastic extensions of more complex bilevel programming models.
17.2.1 Preliminaries

 is a nonempty polyhedron,
is a nonempty polyhedron,  and
and  are vectors,
are vectors,  is a parameter, and the lower level optimal solution set mapping
is a parameter, and the lower level optimal solution set mapping  is given by
is given by 
 and a vector
and a vector  . Let
. Let  denote the mapping
denote the mapping 
Assume dom f ≠ ∅, then f is real-valued
and Lipschitz continuous
on the polyhedron
 . △
. △

 denote the Euclidean unit ball and 0 < Λ < ∞ a constant, then [16, Theorem 4.2] yields
denote the Euclidean unit ball and 0 < Λ < ∞ a constant, then [16, Theorem 4.2] yields 
An alternate proof for Lemma 17.2.1 is given in [17, Theorem 1]. However, the arguments above can be easily extended to lower level problems with convex quadratic objective function and linear constraints. △
Linear programming theory (cf. [18]) provides verifiable necessary and sufficient condition for dom f ≠ ∅:
 such that
such that
- a.
{y | Ay ≤ Tx + z} is nonempty,
- b.
there is some
 satisfying A
⊤u = d and u ≤ 0, and
satisfying A
⊤u = d and u ≤ 0, and
- c.
the function y↦q ⊤y is bounded from below on Ψ(x, z).

is attained for any (x′, z′) ∈ P. △
17.2.2 Bilevel Stochastic Linear Programming Models
 and we assume the following chronology of decision and observation:
and we assume the following chronology of decision and observation: 
 denote the Borel probability measure induced by Z. We shall assume dom f ≠ ∅ and that the lower level problem is feasible for any leader’s decision and any realization of the randomness, i.e.
denote the Borel probability measure induced by Z. We shall assume dom f ≠ ∅ and that the lower level problem is feasible for any leader’s decision and any realization of the randomness, i.e. 
 , where
, where  is a linear subspace of
is a linear subspace of  that contains the constants and satisfies
that contains the constants and satisfies 
![$$\displaystyle \begin{aligned} \min_x \left\{\mathcal{R}[f(x,Z(\cdot))] \; | \; x \in X \right\}. \end{aligned} $$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equ3.png)
 with p ∈ [1, ∞] are natural choices for the domain
with p ∈ [1, ∞] are natural choices for the domain  of
of  . We define
. We define 
 with finite moments
of order p ∈ [1, ∞), and the set
with finite moments
of order p ∈ [1, ∞), and the set 
Assume dom f ≠ ∅ and
 for some p ∈ [1, ∞]. Then the mapping
for some p ∈ [1, ∞]. Then the mapping
 given by F(x) := f(x, Z(⋅)) takes values in
given by F(x) := f(x, Z(⋅)) takes values in
 and is Lipschitz continuous
with respect to the L
p-norm. △
and is Lipschitz continuous
with respect to the L
p-norm. △


 yields
yields 

The mapping  in (17.2.1) can be used to measure the risk associated with the random variable
F(x).
in (17.2.1) can be used to measure the risk associated with the random variable
F(x).
 defined on some linear subspace
defined on some linear subspace  of
of  containing the constants is called a convex risk measure
if the following conditions are fulfilled:
containing the constants is called a convex risk measure
if the following conditions are fulfilled: - a.(Convexity) For any
 and λ ∈ [0, 1] we have
and λ ∈ [0, 1] we have ![$$\displaystyle \begin{aligned}\mathcal{R}[\lambda Y_1 + (1-\lambda)Y_2] \leq \lambda \mathcal{R}[Y_1] + (1 - \lambda) \mathcal{R}[Y_2]. \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equm.png)
- b.
(Monotonicity)
![$$\mathcal {R}[Y_1] \leq \mathcal {R}[Y_2]$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_IEq31.png) for all
for all  satisfying Y
1 ≤ Y
2 with respect to the
satisfying Y
1 ≤ Y
2 with respect to the  -almost sure partial order.
-almost sure partial order. - c.
(Translation equivariance)
![$$\mathcal {R}[Y + t] = \mathcal {R}[Y] + t$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_IEq34.png) for all
for all  and
and  .
.
 is coherent
if the following holds true:
is coherent
if the following holds true: - d.
(Positive homogeneity)
![$$\mathcal {R}[t Y] = t \cdot \mathcal {R}[Y]$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_IEq38.png) for all
for all  and t ∈ [0, ∞). △
and t ∈ [0, ∞). △
A mapping  is called law-invariant
if for all
is called law-invariant
if for all  with
with  we have
we have ![$$\mathcal {R}[Y_1] = \mathcal {R}[Y_2]$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_IEq43.png) . △
. △
Coherent risk measures have been introduced in [19], while the analysis of convex risk measures dates back to [20]. A thorough discussion of their analytical traits is provided in [21]. Below we list some risk measures that are commonly used in stochastic programming (cf. [1, Sect. 6.3.2]).
- (a)The expectation
 ,
, ![$$\displaystyle \begin{aligned}\mathbb{E}[Y] = \int_\Omega Y(\omega)~\mathbb{P}(d\omega), \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equn.png) is a law-invariant and coherent risk measure that turns (17.2.1) into the risk neutral bilevel stochastic program
is a law-invariant and coherent risk measure that turns (17.2.1) into the risk neutral bilevel stochastic program![$$\displaystyle \begin{aligned}\min_x \left\{\mathbb{E}[F(x)] \; | \; x \in X \right\}. \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equo.png)
- (b)The expected excess of orderp ∈ [1, ∞) over a predefined level
 is the mapping
is the mapping  given by
given by ![$$\displaystyle \begin{aligned}\mbox{EE}_{\eta}^p[Y] := \Big( \mathbb{E}\big[\max \lbrace Y - \eta, 0 \rbrace^p \big] \Big)^{1/p}. \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equp.png)
 is law-invariant, convex and nondecreasing, but neither translation-equivariant nor positively homogeneous (cf. [1, Example 6.22]).
is law-invariant, convex and nondecreasing, but neither translation-equivariant nor positively homogeneous (cf. [1, Example 6.22]). - (c)The mean upper semideviation of orderp ∈ [1, ∞) is the mapping
 defined by
defined by ![$$\displaystyle \begin{aligned}\mbox{SD}_\rho^p[Y] := \mathbb{E}[Y] + \rho \cdot \mbox{EE}_{\mathbb{E}[Y]}^p[Y] = \mathbb{E}[Y] + \rho \cdot \Big( \mathbb{E}\big[\max \lbrace \mathbb{E}[Y] - \eta, 0 \rbrace^p \big] \Big)^{1/p}, \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equq.png)
where ρ ∈ (0, 1] is a parameter.
 is a law-invariant coherent risk measure (cf. [1, Example 6.20]).
is a law-invariant coherent risk measure (cf. [1, Example 6.20]). - (d)The excess probability
 over a prescribed target level
over a prescribed target level  given by
given by ![$$\displaystyle \begin{aligned}\mbox{EP}_\eta[Y] = \mathbb{P}[\lbrace \omega \in \Omega \; | \; Y(\omega) > \eta \rbrace], \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equr.png)
is nondecreasing and law-invariant. However, it lacks convexity, translation-equivariance and positive homogeneity (cf. [22, Example 2.29]).
- (e)The Value-at-Risk
 at level α ∈ (0, 1) defined by
at level α ∈ (0, 1) defined by ![$$\displaystyle \begin{aligned}\mbox{VaR}_{\alpha}[Y] := \inf \lbrace \eta \in \mathbb{R} \; | \; \mathbb{P}[\lbrace \omega \in \Omega \; | \; Y(\omega) \leq \eta \rbrace] \geq \alpha \rbrace \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equs.png)
is law-invariant, nondecreasing, translation-equivariant and positively homogeneous, but in general not convex (cf. [23]).
- (f)The Conditional Value-at-Risk
 at level α ∈ (0, 1) given by
at level α ∈ (0, 1) given by ![$$\displaystyle \begin{aligned}\mbox{CVaR}_{\alpha}[Y] := \inf \lbrace \eta + \frac{1}{1-\alpha}\mbox{EE}_{\eta}^1[Y] \; | \; \eta \in \mathbb{R} \rbrace \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equt.png)
is a law-invariant coherent risk measure (cf. [23, Proposition 2]). The variational representation above was established in [24, Theorem 10].
- (g)The entropic risk measure
 defined by
defined by ![$$\displaystyle \begin{aligned}\mbox{Entr}_{\alpha}[Y] := \frac{1}{\alpha} \ln \Big( \mathbb{E} \big[\exp(\alpha Y) \big] \Big), \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equu.png)
where α > 0 is a parameter, is a law-invariant convex (but not coherent) risk measure (cf. [21, Example 4.13, Example 4.34]).
- (h)The worst-case risk measure
 given by
given by ![$$\displaystyle \begin{aligned}\mathcal{R}_{\max}[Y] := \sup_{\omega \in \Omega} Y(\omega) \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equv.png) is law-invariant and coherent (cf. [21, Example 4.8]). This choice of
is law-invariant and coherent (cf. [21, Example 4.8]). This choice of in (17.2.1) leads to the bilevel robust problem
in (17.2.1) leads to the bilevel robust problem
![$$\displaystyle \begin{aligned}\min_x \left\{\mathcal{R}_{\max}[F(x)] \; | \; x \in X \right\}. \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equw.png)
Note that
 only depends on the so called uncertainty set
only depends on the so called uncertainty set
 . Thus, a bilevel robust problem can be formulated without knowledge of the distribution of the uncertain parameter. In robust optimization, the uncertainty set is often assumed to be finite, polyhedral or ellipsoidal (cf. [25]).
. Thus, a bilevel robust problem can be formulated without knowledge of the distribution of the uncertain parameter. In robust optimization, the uncertainty set is often assumed to be finite, polyhedral or ellipsoidal (cf. [25]).
 is a convex cone for any fixed p ∈ [1, ∞]. In particular, if
is a convex cone for any fixed p ∈ [1, ∞]. In particular, if  is a convex (coherent) risk measure, then so is
is a convex (coherent) risk measure, then so is  for any ρ ≥ 0. The mean-risk bilevel stochastic programming model
for any ρ ≥ 0. The mean-risk bilevel stochastic programming model
![$$\displaystyle \begin{aligned}\min_x \left\{\mathbb{E}[F(x)] + \rho \cdot \mathcal{R}[F(x)] \; | \; x \in X \right\} \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equx.png)
![$$\displaystyle \begin{aligned}\min \left\{ \mathcal{R}[\min \Psi(x,Z)] \; | \; 1 \leq x \leq 6 \right\}, \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equy.png)

![$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathbb{E}[\min \Psi(x,Z)] &\displaystyle = \int_{-0.5}^{0.5} \int_{-0.5}^{0.5} x + 2 + z_1~dz_1~dz_2 \\ &\displaystyle = x+2 \end{array} \end{aligned} $$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equ5.png)
![$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathbb{E}[\min \Psi(x,Z)] &\displaystyle = \int_{-0.5}^{2x-6} \int_{-0.5}^{-2x + 6.5 + z_2} x + 2 + z_1~dz_1~dz_2 \\ &\displaystyle + \int_{2x-6}^{0.5} \int_{-0.5}^{0.5} x + 2 + z_1~dz_1~dz_2 \\ &\displaystyle +\int_{6-2x}^{0.5} \int_{-0.5}^{2x - 6.5 + z_1} -x + 8.5 + z_2~dz_2~dz_1 \\ &\displaystyle = -\frac{4}{3}x^3 + 11x^2 - \frac{117}{4} x + \frac{1427}{48} \end{array} \end{aligned} $$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equ6.png)
![$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathbb{E}[\min \Psi(x,Z)] &\displaystyle = \int_{2x-7}^{0.5} \int_{-0.5}^{-2x + 6.5 + z_2} x + 2 + z_1~dz_1~dz_2 \\ &\displaystyle +\int_{-0.5}^{7-2x} \int_{-0.5}^{2x - 6.5 + z_1} -x + 8.5 + z_2~dz_2~dz_1 \\ &\displaystyle +\int_{7-2x}^{0.5} \int_{-0.5}^{0.5} -x + 8.5 + z_2~dz_2~dz_1 \\ &\displaystyle = \frac{4}{3} x^3 - 15 x^2 + \frac{221}{4} x - \frac{989}{16} \end{array} \end{aligned} $$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equ7.png)
![$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathbb{E}[\min \Psi(x,Z)] &\displaystyle = \int_{-0.5}^{0.5} \int_{-0.5}^{0.5} -x + 8.5 + z_2~dz_2~dz_1 \\ &\displaystyle = -x + 8.5. \end{array} \end{aligned} $$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equ8.png)
![$$\mathbb {E}[\min \Psi (\cdot \,,Z)]$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_IEq62.png) is piecewise polynomial, non-convex and non-differentiable
. It is easy to check that x
∗ = 6 is a global minimizer of the risk-neutral model
is piecewise polynomial, non-convex and non-differentiable
. It is easy to check that x
∗ = 6 is a global minimizer of the risk-neutral model ![$$\displaystyle \begin{aligned}\min \left\{ \mathbb{E}[\min \Psi(x,Z)] \; | \; 1 \leq x \leq 6 \right\}. \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equaa.png)
![$$\displaystyle \begin{aligned}\min \left\{ \mathcal{R}_{max}[\min \Psi(x,Z)] \; | \; 1 \leq x \leq 6 \right\}. \end{aligned} $$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equab.png)
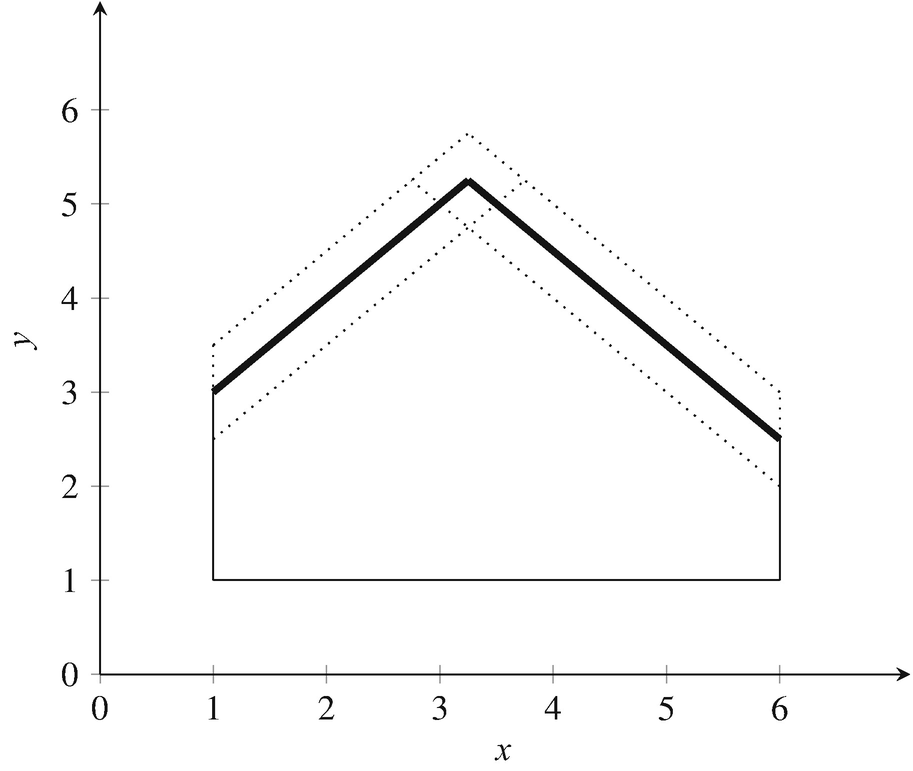
The bold line depicts the graph of Ψ(⋅ , (0, 0)), while the dotted lines correspond to the graphs of Ψ(⋅ , (±0.5, ±0.5)) and Ψ(⋅ , (∓0.5, ±0.5))
17.2.3 Continuity and Differentiability
Continuity properties of  carry over to Lipschitzian
properties of
carry over to Lipschitzian
properties of  ,
, ![$$\mathcal {Q}_{\mathcal {R}}(x) := \mathcal {R}[F(x)]$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_IEq65.png) .
.
 for some p ∈ [1, ∞]. Then the following statements hold true for any
for some p ∈ [1, ∞]. Then the following statements hold true for any

- a.
 is locally Lipschitz continuous if
is locally Lipschitz continuous if
 is convex and continuous.
is convex and continuous.
- b.
 is locally Lipschitz continuous if
is locally Lipschitz continuous if
 is convex and nondecreasing.
is convex and nondecreasing.
- c.
 is locally Lipschitz continuous if
is locally Lipschitz continuous if
 is a convex risk measure
.
is a convex risk measure
. - d.
 is Lipschitz continuous if
is Lipschitz continuous if
 is Lipschitz continuous.
is Lipschitz continuous.
- e.
 is Lipschitz continuous if
is Lipschitz continuous if
 is a coherent risk measure.△
is a coherent risk measure.△
- a.
It is well-known that any real-valued convex and continuous mapping on a normed space is locally Lipschitz continuous (cf. [26]). The result is thus an immediate consequence of Lemma 17.2.4.
- b.
Any real-valued, convex and nondecreasing functional on the Banach lattice
 is continuous (see e.g. [27, Theorem 4.1]).
is continuous (see e.g. [27, Theorem 4.1]). - c.
By definition, any convex risk measure is convex and nondecreasing.
- d.
This is a straightforward conclusion from Lemma 17.2.4.
- e.
Any coherent risk measure on
 is Lipschitz continuous by Inoue [28, Lemma 2.1].
is Lipschitz continuous by Inoue [28, Lemma 2.1].
Any coherent risk measure
 is Lipschitz continuous
with constant 1 by Föllmer and Schied [21, Lemma 4.3]. Concrete Lipschitz constants for continuous coherent law-invariant risk measures
is Lipschitz continuous
with constant 1 by Föllmer and Schied [21, Lemma 4.3]. Concrete Lipschitz constants for continuous coherent law-invariant risk measures  with p ∈ [1, ∞) may be obtained from representation results (see e.g. [29]). △
with p ∈ [1, ∞) may be obtained from representation results (see e.g. [29]). △
Proposition 17.2.8 allows to formulate sufficient conditions for the existence of optimal solutions to the bilevel stochastic linear program (17.2.1):
Assume dom f ≠ ∅,
 for some p ∈ [1, ∞] and let X ⊆ P
Zbe nonempty and compact. Then (17.2.1) is solvable for any convex and nondecreasing mapping
for some p ∈ [1, ∞] and let X ⊆ P
Zbe nonempty and compact. Then (17.2.1) is solvable for any convex and nondecreasing mapping
 . △
. △
Due to the lack of convexity, Proposition 17.2.8 and the subsequent Corollary do not apply to the excess probability and the Value-at-Risk. However, invoking Lemma 17.2.1, the arguments used in the proof of [30, Proposition 3.3] can adapted to the setting of bilevel stochastic linear programming:
 , then
, then
 is lower semicontinuous on P
Zand continuous at any x ∈ P
Zsatisfying
is lower semicontinuous on P
Zand continuous at any x ∈ P
Zsatisfying
![$$\displaystyle \begin{aligned}\mu_Z[\lbrace z \in \mathbb{R} \; | \; f(x,z) = \eta \rbrace] = 0. \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equac.png)
![$$\displaystyle \begin{aligned}\min_x \left\{ \mathit{\mbox{EP}}_\eta [F(x)] \; | \; x \in X \right\} \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equad.png)
is solvable.△
 has been analyzed in [17, Theorem 2]:
has been analyzed in [17, Theorem 2]:
 is continuous. Moreover, let X ⊆ P
Zbe nonempty and compact. Then
is continuous. Moreover, let X ⊆ P
Zbe nonempty and compact. Then
![$$\displaystyle \begin{aligned}\min_x \left\{\mathit{\mbox{VaR}}_\alpha[F(x)] \; | \; x \in X \right\} \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equae.png)
is solvable.△
For specific risk measures, sufficient conditions for differentiability
of  have been investigated in [31].
have been investigated in [31].
Assume dom f ≠ ∅ and that
 is absolutely continuous with respect to the Lebesgue measure. Fix any
is absolutely continuous with respect to the Lebesgue measure. Fix any
 , then
, then
 and
and
 are continuously differentiable at any x
0 ∈int P
Z. Furthermore, for any ρ ∈ [0, 1),
are continuously differentiable at any x
0 ∈int P
Z. Furthermore, for any ρ ∈ [0, 1),  is continuously differentiable at any x
0 ∈int P
Zsatisfying
is continuously differentiable at any x
0 ∈int P
Zsatisfying
 . △
. △
Theorems 3.7, 3.8 and 3.9 in [31] provide more involved sufficient conditions for continuous differentiability of  ,
,  and
and  that do not require μ
Z to be absolutely continuous.△
that do not require μ
Z to be absolutely continuous.△

 is not absolutely continuous with respect to the Lebesgue measure. △
is not absolutely continuous with respect to the Lebesgue measure. △In the presence of differentiability, necessary optimality conditions for (17.2.1) can be formulated in terms of directional derivatives (cf. [31, Corollary 3.10]).
 and X ⊆ P
Z. Furthermore, let x
0 ∈ X be a local minimizer of problem (17.2.1) and assume that
and X ⊆ P
Z. Furthermore, let x
0 ∈ X be a local minimizer of problem (17.2.1) and assume that
 is differentiable at x
0. Then
is differentiable at x
0. Then

![$$\displaystyle \begin{aligned}v \in \lbrace v \in \mathbb{R}^n \; | \; \exists \epsilon_0 > 0: \; x_0 + \epsilon v \in X \; \forall \epsilon \in [0,\epsilon_0] \rbrace. \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equah.png)
△
17.2.4 Stability
While we have only considered  as a functions of the leader’s decision x so far, it also depends on the underlying probability measure μ
Z. In stochastic programming, incomplete information about the true underlying distribution or the need for computational efficiency may lead to optimization models that employ an approximation of μ
Z. This section analysis deals with the behaviour of optimal values and (local) optimal solution sets of (17.2.1) under perturbations of the underlying distribution.
as a functions of the leader’s decision x so far, it also depends on the underlying probability measure μ
Z. In stochastic programming, incomplete information about the true underlying distribution or the need for computational efficiency may lead to optimization models that employ an approximation of μ
Z. This section analysis deals with the behaviour of optimal values and (local) optimal solution sets of (17.2.1) under perturbations of the underlying distribution.

 are given in [17, Corollary 1] and [17, Corollary 2]. The following characterization is a direct consequence of Gordan’s Lemma (cf. [32]):
are given in [17, Corollary 1] and [17, Corollary 2]. The following characterization is a direct consequence of Gordan’s Lemma (cf. [32]):
 holds if and only if u = 0 is the only non-negative solution to A
⊤u = 0. △
holds if and only if u = 0 is the only non-negative solution to A
⊤u = 0. △
Throughout this section, we shall consider the situation that  with p ∈ [1, ∞) is law-invariant, convex and nondecreasing. Furthermore, for the sake of notational simplicity (cf. [31, Remark 4.1]), we assume that the probability space
with p ∈ [1, ∞) is law-invariant, convex and nondecreasing. Furthermore, for the sake of notational simplicity (cf. [31, Remark 4.1]), we assume that the probability space
 is atomless, i.e. for any
is atomless, i.e. for any  with
with ![$$\mathbb {P}[A] > 0$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_IEq107.png) there exists some
there exists some  with
with  and
and ![$$\mathbb {P}[A] > \mathbb {P}[B] > 0$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_IEq110.png) .
.
 , we have
, we have  , where
, where  denotes the Dirac measure at x. The atomlessness of
denotes the Dirac measure at x. The atomlessness of  ensures that there exists some
ensures that there exists some  such that
such that  . Thus, we may consider the mapping
. Thus, we may consider the mapping  defined by
defined by ![$$\displaystyle \begin{aligned}\mathcal{Q}_{\mathcal{R}}(x,\mu) := \mathcal{R}[Y_{(x,\mu)}]. \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equaj.png)
 .
.
 we introduce the localized optimal value function
we introduce the localized optimal value function  ,
, 
 ,
, 
Given  and an open set
and an open set  , ϕ
V(μ) is called a complete local minimizing (CLM) set
of (Pμ
) w.r.t. V if ∅ ≠ ϕ
V(μ) ⊆ V . △
, ϕ
V(μ) is called a complete local minimizing (CLM) set
of (Pμ
) w.r.t. V if ∅ ≠ ϕ
V(μ) ⊆ V . △
The set of global optimal solutions  and any set of isolated minimizers are CLM sets. However, sets of strict local minimizers may fail to be CLM sets (cf. [33]). △
and any set of isolated minimizers are CLM sets. However, sets of strict local minimizers may fail to be CLM sets (cf. [33]). △
 with the topology of weak convergence
, i.e. the topology, where a sequence
with the topology of weak convergence
, i.e. the topology, where a sequence  converges weakly to
converges weakly to  , written
, written 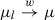 , if and only if
, if and only if 
 (cf. [34]). The example below (cf. [22, Example 3.2]) shows that even
(cf. [34]). The example below (cf. [22, Example 3.2]) shows that even  may fail to be weakly continuous on the entire space
may fail to be weakly continuous on the entire space  .
.
 and
and  holds for any (x, z). Assume that μ is the Dirac measure at 0, then the above problem can be rewritten as
holds for any (x, z). Assume that μ is the Dirac measure at 0, then the above problem can be rewritten as 
 converges weakly to δ
0, replacing μ with μ
l yields the problem
converges weakly to δ
0, replacing μ with μ
l yields the problem 
 .
.We shall follow the approach of [22, 31] and [35] and confine the stability analysis to locally uniformly ∥⋅∥p-integrating sets.
 is said to be locally uniformly ∥⋅∥p-integrating if for any 𝜖 > 0 there exists some open neighborhood
is said to be locally uniformly ∥⋅∥p-integrating if for any 𝜖 > 0 there exists some open neighborhood  of μ w.r.t. the topology of weak convergence such that
of μ w.r.t. the topology of weak convergence such that 
△
A detailed discussion of locally uniformly ∥⋅∥p-integrating sets and their generalizations is provided in [21, 36, 37], and [38]. The following examples demonstrate the relevance of the concept.
- (a)Fix κ, 𝜖 > 0. Then by Föllmer and Schied [21, Corollary A.47 (c)], the set

of Borel probability measures with uniformly bounded moments of order p + 𝜖 is locally uniformly ∥⋅∥p-integrating.
- (b)
of Borel probability measures whose support is contained in Ξ is locally uniformly ∥⋅∥p-integrating.
The following result has been established in [31, Theorem 4.7]:
Assume dom f ≠ ∅ and
 . Let
. Let
 be locally uniformly ∥⋅∥p-integrating, then
be locally uniformly ∥⋅∥p-integrating, then
- a.
 is real-valued and weakly continuous.
is real-valued and weakly continuous.
- b.
 is weakly upper semicontinuous.
is weakly upper semicontinuous.
In addition, assume that
 is such that ϕ
V(μ
0) is a CLM set of
is such that ϕ
V(μ
0) is a CLM set of
 w.r.t. some open bounded set
w.r.t. some open bounded set
 . Then the following statements hold true:
. Then the following statements hold true:
- c.
 is weakly continuous at μ
0.
is weakly continuous at μ
0. - d.
 is weakly upper semicontinuous at μ
0in the sense of Berge (cf. [
39]), i.e. for any open set
is weakly upper semicontinuous at μ
0in the sense of Berge (cf. [
39]), i.e. for any open set
 with
with
 there exists a weakly open neighborhood
there exists a weakly open neighborhood
 of μ
0such that
of μ
0such that
 for all
for all
 .
. - e.
There exists some weakly open neighborhood
 of μ
0such that ϕ
V(μ) is a CLM set for (Pμ
) w.r.t. V for any
of μ
0such that ϕ
V(μ) is a CLM set for (Pμ
) w.r.t. V for any
 . △
. △
Under the assumptions of Theorem 17.2.21d., any accumulation point x of a sequence local optimal solutions x
l ∈ ϕ
V(μ
l) as 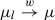 ,
,  , is a local optimal solution of (Pμ
). A detailed discussion of Berge’s notion of upper semicontinuity and related concepts is provided in [40, Chap. 5].△
, is a local optimal solution of (Pμ
). A detailed discussion of Berge’s notion of upper semicontinuity and related concepts is provided in [40, Chap. 5].△
As any Borel probability measure is the weak limit of a sequence of measures having finite support, Theorem 17.2.21 justifies an approach where the true underlying measure is approximated by a sequence of finite discrete ones. It is well known that approximation schemes based on discretization via empirical estimation [41, 42] or conditional expectations [43, 44] produce weakly converging sequences of discrete probability measures under mild assumptions.
17.2.5 Stochastic Dominance Constraints

 is minimized over some subset of random variables
of acceptable risk:
is minimized over some subset of random variables
of acceptable risk: 
 . The following cases are of particular interest (cf. [1, pp. 90–91]) :
. The following cases are of particular interest (cf. [1, pp. 90–91]) :- (a)
 is given by probabilistic constraints, i.e.
is given by probabilistic constraints, i.e. ![$$\displaystyle \begin{aligned}\mathcal{A}_{\text{pc}} = \{h \in f(X,Z) \; | \; \mathbb{P}[h \leq \beta_j] \geq p_j \; \forall j= 1, \ldots, l\} \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equax.png)
for bounds
 and safety levels p
1, …, p
l ∈ (0, 1).
and safety levels p
1, …, p
l ∈ (0, 1). - (b)
 is given by first-order stochastic dominance constraints, i.e.
is given by first-order stochastic dominance constraints, i.e. ![$$\displaystyle \begin{aligned}\mathcal{A}_{\text{fo}} = \{h \in f(X,Z) \; | \; \mathbb{P}[h \leq \beta] \geq \mathbb{P}[b \leq \beta] \; \forall \beta \in \mathbb{R}\}, \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equay.png)
where
 is a given benchmark variable. If b is discrete with a finite number of realizations, it is sufficient to impose the relation
is a given benchmark variable. If b is discrete with a finite number of realizations, it is sufficient to impose the relation ![$$\mathbb {P}[h \leq \beta ] \geq \mathbb {P}[b \leq \beta ]$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_IEq165.png) for any β in a finite subset of
for any β in a finite subset of  . In this case,
. In this case,  admits a description by a finite system of probabilistic constraints.
admits a description by a finite system of probabilistic constraints. - (c)
 is given by second-order stochastic dominance constraints, i.e.
is given by second-order stochastic dominance constraints, i.e. ![$$\displaystyle \begin{aligned}\mathcal{A}_{\text{so}} = \{h \in f(X,Z) \; | \; \mathbb{E}[\max\{h - \eta, 0\}] \leq \mathbb{E}[\max\{b - \eta, 0\}] \; \forall \eta \in \mathbb{R}\}, \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equaz.png)
where
 is a given benchmark variable.
is a given benchmark variable.
A discussion of general models involving probabilistic or stochastic dominance constraints can be found in [1, Chap. 8] and [45, Chap. 8.3].
 denote the distribution of the benchmark variable b. Then the feasible set under first-order stochastic dominance constraints admits the representation
denote the distribution of the benchmark variable b. Then the feasible set under first-order stochastic dominance constraints admits the representation ![$$\displaystyle \begin{aligned}\left\{ x \in X \; | \; \mu_Z\big[ \lbrace z \in \mathbb{R}^s \; | \; f(x,z) \leq \beta \rbrace \big] \geq \nu\big[ \lbrace b \in \mathbb{R} \; | \; b \leq \beta \rbrace \big] \; \forall \beta \in \mathbb{R} \right\}. \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equba.png)
 and
and  , the feasible set takes the form
, the feasible set takes the form 
 defined by
defined by ![$$\displaystyle \begin{aligned}\mathcal{C}_1(\mu) = \left\{ x \in X \; | \; \mu \big[ \lbrace z \in \mathbb{R}^s \; | \; f(x,z) \leq \beta \rbrace \big] \geq \nu\big[ \lbrace b \in \mathbb{R} \; | \; b \leq \beta \rbrace \big] \; \forall \beta \in \mathbb{R} \right\}. \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equbc.png)
 given by
given by 
Invoking Lemma 17.2.1, the following result can be obtained by adapting the proofs of [46, Proposition 2.1] and [47, Proposition 2.2] :
 . Then the following statements hold true:
. Then the following statements hold true:
- a.
The multifunction C 1is closed w.r.t. the topology of weak convergence , i.e. for any sequences
 and
and
 with
with
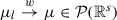 ,
,  for l →∞ and x
l ∈ C
1(μ
l) for all
for l →∞ and x
l ∈ C
1(μ
l) for all
 it holds true that x ∈ C
1(μ).
it holds true that x ∈ C
1(μ). - b.
Additionally assume that
 , then the multifunction C
2is closed w.r.t. the topology of weak convergence.△
, then the multifunction C
2is closed w.r.t. the topology of weak convergence.△
By considering the constant sequence μ
l = μ for all  we obtain the closedness of the sets C
1(μ) and C
2(μ) under the conditions of Proposition 17.2.24. The closedness of the multifunctions C
1 and C
2 is also the key to proving the following stability result (cf. [46, Proposition 2.5]):
we obtain the closedness of the sets C
1(μ) and C
2(μ) under the conditions of Proposition 17.2.24. The closedness of the multifunctions C
1 and C
2 is also the key to proving the following stability result (cf. [46, Proposition 2.5]):
 and that X is nonempty and compact. Moreover, let g be lower semicontinuous. Then the following statements hold true:
and that X is nonempty and compact. Moreover, let g be lower semicontinuous. Then the following statements hold true:
- a.The optimal value function
 given by
given by

is weakly lower semicontinuous on dom C 1.
- b.Additionally assume
 , then the function
, then the function
 given by
given by

is weakly lower semicontinuous on dom C 2. △
17.2.6 Finite Discrete Distributions
 and respective probabilities π
1, …, π
K ∈ (0, 1]. Let I denote the index set {1, …, K}, then P
Z takes the form
and respective probabilities π
1, …, π
K ∈ (0, 1]. Let I denote the index set {1, …, K}, then P
Z takes the form 
 holds for some k ∈ I. Then the probability of f(x
0, Z(ω)) = ∞ is a least π
k > 0, i.e. x
0 should be considered as infeasible for problem (17.2.1). Consequently, X ⊆ P
Z can be understood as an induced constraint. Note that X ∩ P
Z is a polyhedron if X is a polyhedron.
holds for some k ∈ I. Then the probability of f(x
0, Z(ω)) = ∞ is a least π
k > 0, i.e. x
0 should be considered as infeasible for problem (17.2.1). Consequently, X ⊆ P
Z can be understood as an induced constraint. Note that X ∩ P
Z is a polyhedron if X is a polyhedron.In this setting, the bilevel stochastic linear problem can be reduced to a standard bilevel program, which allows to adapt optimality conditions and algorithms designed for the deterministic case (cf. [48]).
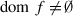 ,
, 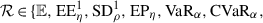
 and let X ⊆ P
Zbe a polyhedron. If
and let X ⊆ P
Zbe a polyhedron. If
 , additionally assume that X bounded. Then for any parameter β, there exists a constant M > 0 such that the bilevel stochastic linear problem
, additionally assume that X bounded. Then for any parameter β, there exists a constant M > 0 such that the bilevel stochastic linear problem
![$$\displaystyle \begin{aligned}\min_x \left\{ \mathcal{R}[F(x)] \; | \; x \in X \right\} \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equbh.png)


 with
with

Equivalent bilevel linear programs
| β | w | a(x, w) | b(x, w) |
|---|---|---|---|---|
|
| c ⊤x+∑k ∈ Iπ kq ⊤y k | ||
|
|
| ∑k ∈ Iπ kv k |
|
| ρ ∈ (0, 1] |
|
|
|
EPη |
|
| ∑k ∈ Iπ kθ k | Mθ k−c ⊤x−q ⊤y k+η |
VaRα | α ∈ (0, 1) |
| ∑k ∈ Iπ kθ k |
|
CVaRα | α ∈ (0, 1) |
|
| cf. |
|
| maxk ∈ Ic ⊤x+q ⊤y k |
For  , we refer to [31, Section 5].
, we refer to [31, Section 5].
![$$\mbox{EP}_{\eta }[F(x)] = \mathbb {P}\left [c^\top x + \inf _y \{q^\top y \; | \; y \in \Psi (x, Z(\cdot ))\} > \eta \right ]$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_IEq215.png) . Fix
. Fix  such that
such that 


 , the expression
, the expression ![$$\mathbb {P}[f(x,Z(\cdot )) \leq \eta ]$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_IEq218.png) equals
equals 


 and the result follows from
and the result follows from  . □
. □- a.
The equivalent standard bilevel problem is linear provided that
 .
. - b.
Analogous to [31, Remarks 5.2, 5.4], the inner minimization problems of the standard bilevel linear programs for
 can be decomposed into K scenario problems that only differ w.r.t. the right-hand side
of the constraint system. For the other models, a similar decomposition is possible after Lagrangian relaxation of the coupling constraints involving different scenarios.
can be decomposed into K scenario problems that only differ w.r.t. the right-hand side
of the constraint system. For the other models, a similar decomposition is possible after Lagrangian relaxation of the coupling constraints involving different scenarios. - c.
For
 , every evaluation of the objective function in the standard bilevel linear program corresponds to solving a bilevel linear problem
with scalar upper level variable η.
, every evaluation of the objective function in the standard bilevel linear program corresponds to solving a bilevel linear problem
with scalar upper level variable η. - d.
Alternate models for
 are given in [17] and [49], where the considered bilevel stochastic linear problem is reduced to a mixed-integer nonlinear program and a mathematical programming problem with equilibrium constraints, respectively. A mean-risk model with
are given in [17] and [49], where the considered bilevel stochastic linear problem is reduced to a mixed-integer nonlinear program and a mathematical programming problem with equilibrium constraints, respectively. A mean-risk model with  is used in [5, Sect. III].△
is used in [5, Sect. III].△
Similar reformulations can be obtained for the models discussed in Sect. 17.2.5 if we assume that the disutility function is linear.


![$$\bar {a}_j := 1 - \mathbb {P}[b \leq a_j]$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_IEq226.png) and
and
 .
. Equivalent programs, notation as in the Example in Sect. 17.2.5
| γ | w j | a(w j) |
| δ j |
|---|---|---|---|---|---|
|
|
| ∑k ∈ Iπ kθ kj |
| p j |
|
|
| ∑k ∈ Iπ kθ kj |
|
|
|
|
| ∑k ∈ Iπ kv kj |
|
|
△
17.2.7 Solution Approaches
To solve bilevel problems, it is very common to use a single level reformulation. Often the lower level minimality condition is replaced by its Karush-Kuhn-Tucker or Fritz John conditions and the bilevel problem is reduced to a mathematical programming problem with equilibrium constraints (cf. [5, 17], [48, Chap. 3.5.1]).
 , the equivalent standard bilevel programs in Proposition 17.2.26 can be all restated as
, the equivalent standard bilevel programs in Proposition 17.2.26 can be all restated as 
 is given by Ψ(u) = Argminw{t
⊤w | Ww ≤ Bu + b} for vectors
is given by Ψ(u) = Argminw{t
⊤w | Ww ≤ Bu + b} for vectors  ,
,  and
and  , matrices
, matrices  and
and  , and
, and  is a nonempty polyhedron. The usage of the KKT conditions of the lower level problem leads to the single-level problem
is a nonempty polyhedron. The usage of the KKT conditions of the lower level problem leads to the single-level problem 
In [31, Sect. 6] it is also shown that  is a local minimizer of the optimistic formulation, if
is a local minimizer of the optimistic formulation, if  is an accumulation point of a sequence
is an accumulation point of a sequence  of local minimizers of problem P(ε
n) for ε
n ↓ 0.
of local minimizers of problem P(ε
n) for ε
n ↓ 0.
In the risk-neutral setting, problem (17.2.2) exhibits a block-structure (cf. Remark 17.2.27 b.). Adapting the solution method for general linear complementarity problems proposed in [50], this special structure has been used in [11, Chap. 6] to construct an efficient algorithm for the global resolution of bilevel stochastic linear problems based on dual decomposition.
Utilizing the lower level value function, problem (17.2.2) can be reformulated as a single level quasiconcave optimization problem (cf. [48, Chap. 3.6.5]). Solution methods based on a branch-and-bound scheme have been proposed in [51] and [52]. However, without modifications, these algorithms fail to exploit the block structure arising in risk-neutral bilevel stochastic linear optimization models (cf. [11, Chap. 4.2]). △
17.3 Two-Stage Stochastic Bilevel Programs
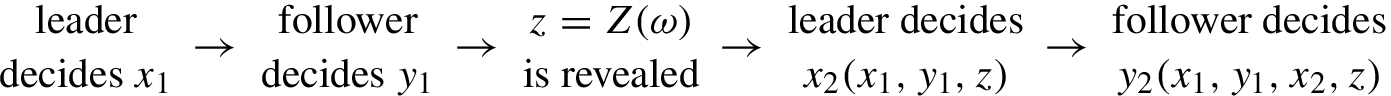
The bilevel stochastic linear problems considered in Sect. 17.2 can be understood as special two-stage bilevel programs, where the follower’s first-stage and the leader’s second stage decision do not influence the outcome. △
 of tariff and tariff-free arcs, respectively, and the leaders is maximizing the revenue raised from tariffs, knowing that user flows are assigned to cheapest paths. In [53], this situation is modeled as a bilevel program
of tariff and tariff-free arcs, respectively, and the leaders is maximizing the revenue raised from tariffs, knowing that user flows are assigned to cheapest paths. In [53], this situation is modeled as a bilevel program 
![$$\displaystyle \begin{aligned}\Psi(x, c, d, b) := \underset{y,\bar{y}}{\mbox{Argmin}} \left\{ \sum_{k \in K} \left[ (c + x)^\top y^k + \bar{c}^\top \bar{y}^k \right] \; \Big| \; \begin{array}{l} y, \bar{y} \geq 0, \\ Ay^k + \bar{A} \bar{y}^k = b^k \; \forall k \in K \end{array} \right\}, \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equbu.png)
 are the flows of commodity k on the tariff and tariff-free arcs, respectively. Moreover, c and
are the flows of commodity k on the tariff and tariff-free arcs, respectively. Moreover, c and  are the fixed costs on θ and
are the fixed costs on θ and  , respectively,
, respectively,  denotes the node-arc incidence matrix and the vectors b
k defined by
denotes the node-arc incidence matrix and the vectors b
k defined by 
![$$\displaystyle \begin{aligned} \text{``}\max_{x_1}\text{''} \left\{ \sum_{k \in K} x_1^\top y^k_1 + \mathbb{E}[\Phi(x_1, Z(\cdot))] \; | \; (y_1,\bar{y}_1) \in \Psi(x_1,c_1,d_1,b_1) \right\}, \end{aligned} $$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equ13.png)



17.4 Challenges
We shall highlight some aspects of bilevel stochastic programming that are highly deserving of future research:
The first paper on bilevel stochastic programming has already outlined the basic principles as well as existence and sensitivity results for risk neutral models (cf. [2]). Nevertheless, so far, most of the research on bilevel stochastic nonlinear programming is still concerned with the risk-neutral case. Notable exceptions are [5] and [8], where models involving the Conditional Value-at-Risk are considered. In the first paper the problem of maximizing the medium-term revenue of an electricity retailer under uncertain pool prices, demand, and competitor prices is modeled as a bilevel stochastic quadratic problem, while the latter explores links between electricity swing option pricing and bilevel stochastic optimization. However, there exists no systematic analysis of bilevel stochastic nonlinear problems in the broader framework of coherent risk measures or higher stochastic dominance constraints. Future research may also consider distributionally robust models (cf. [54]).
Under finite discrete distributions many bilevel stochastic problems can be reformulated as standard bilevel programs. While this reformulation entails a blow-up of the dimension which is usually linear in the number of scenarios, the resulting problems often exhibit (quasi) block structures (cf. Remark 17.2.27b., [2]). For risk-neutral bilevel stochastic linear problems, [11, Chap. 6] utilizes these structures to enhance the mixed integer programming based solution algorithm of [50] resulting in a significant speed-up. Based on the structural similarities an analogous approach should be possible for risk-averse models after Lagrangian relaxation of coupling constraints.
While the analysis in the vast majority of papers on stochastic programming is confined to the case of purely exogenous stochasticity, this assumption is known to be unrealistic in economic models, where the decision maker holds market power. Therefore, models with decision dependent distributions are of particular interest in view of stochastic Stackelberg games (cf. [55]).
The second author thanks the Deutsche Forschungsgemeinschaft for its support via the Collaborative Research Center TRR 154.

![$$\displaystyle \begin{aligned}\{\mu \in \mathcal{P}(\mathbb{R}^s) \; | \; \mu[\Xi] = 1\} \end{aligned}$$](../images/480569_1_En_17_Chapter/480569_1_En_17_Chapter_TeX_Equas.png)







































