7.1 Introduction
Bilevel optimization has been well recognized as a theoretically very challenging and practically important area of applied mathematics. We refer the reader to the monographs [2, 6, 14, 30, 41], the extensive bibliographies and commentaries therein, as well as to the advanced material included in this book for various approaches, theoretical and numerical results, and a variety of practical applications of bilevel optimization and related topics.
One of the characteristic features of bilevel optimization problems is their intrinsic nonsmoothness, even if their initial data are described by linear functions. This makes natural to develop an approach of modern variational analysis and generalized differentiation to the study and applications of major models in bilevel optimization. It has been done in numerous publications, which are presented and analyzed in the author’s recent book [30].
The main goal we pursue here is to overview this approach together with the corresponding machinery of variational analysis and to apply it to deriving necessary optimality conditions in optimistic bilevel models with Lipschitzian data while also commenting on other versions in bilevel optimization with posting open questions. To make this chapter largely self-contained and more accessible for the reader, we present here the basic background from variational analysis and generalized differentiation, which is needed for applications to bilevel optimization. For brevity and simplicity we confine ourselves to problems in finite-dimensional spaces.
The rest of this work is organized as follows. In Sect. 7.2 we recall those constructions of generalized differentiation in variational analysis, which are broadly used in the subsequent text. Section 7.3 presents the fundamental extremal principle that is behind generalized differential calculus and applications to optimization in the geometric approach to variational analysis developed in [29, 30]. Section 7.4 is devoted to deriving—via the extremal principle—the two basic calculus rules, which are particularly useful for applications to optimality conditions. In Sect. 7.5 we establish subdifferential evaluations and efficient conditions that ensure the local Lipschitz continuity of optimal value functions in general problems of parametric optimization. These results are crucial for variational applications to bilevel programming.
To proceed with such applications, we first consider in Sect. 7.6 problems of nondifferentiable programming with Lipschitzian data. Subdifferential necessary optimality conditions for Lipschitzian programs are derived there by using the extremal principle and calculus rules. Section 7.7 contains the formulation of the bilevel optimization problems under consideration and the description of the variational approach to their study. Based on this approach and subdifferentiation of the optimal value functions for lower-level problems, we establish in Sect. 7.8 necessary optimality conditions for Lipschitzian bilevel programs. The other developments in this direction for bilevel optimization problems with Lipschitzian data is presented in Sect. 7.9 by using the subdifferential difference rule based on a certain variational technique. The concluding Sect. 7.10 discusses further perspectives of employing concepts and techniques of variational analysis to bilevel optimization with formulations of some open questions.
Throughout this chapter we use the standard notation and terminology of variational analysis and generalized differentiation; see, e.g., [29, 30, 40].
7.2 Basic Constructions of Generalized Differentiation
Here we present the basic definitions of generalized normals to sets, coderivatives of set-valued mappings, and subgradients of extended-real-valued functions initiated by the author [26] that are predominantly used in what follows. The reader is referred to the books [29, 30, 40] for more details. Developing a geometric approach to generalized differentiation, we start with normals to sets, then continue with coderivatives of (set-valued and single-valued) mappings, and finally pass to subgradients of extended-real-valued functions.
 , we always suppose without loss of generality that it is locally closed around the reference point
, we always suppose without loss of generality that it is locally closed around the reference point  . For each
. For each  close to
close to  consider its (nonempty) Euclidean projector to Ω defined by
consider its (nonempty) Euclidean projector to Ω defined by 
 is
is 
 . Nevertheless, this normal cone and the associated coderivatives of mappings and subdifferentials of functions enjoy comprehensive calculus rules due to variational/extremal principles of variational analysis. Note that
. Nevertheless, this normal cone and the associated coderivatives of mappings and subdifferentials of functions enjoy comprehensive calculus rules due to variational/extremal principles of variational analysis. Note that  if and only if
if and only if  is a boundary point of Ω.
is a boundary point of Ω. . Given x ∈ Ω close to
. Given x ∈ Ω close to  , the prenormal cone to Ω at x (known also as the regular or Fréchet normal cone) is defined by
, the prenormal cone to Ω at x (known also as the regular or Fréchet normal cone) is defined by 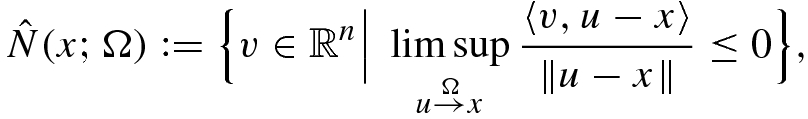
 means that u → x with u ∈ Ω. Then the prenormal cone (7.2.2) is always closed and convex while may collapse to {0} at boundary points of closed sets, which in fact contradicts the very meaning of generalized normals. If Ω is convex, then both normal and prenormal cones reduce to the normal cone of convex analysis. In general we have
means that u → x with u ∈ Ω. Then the prenormal cone (7.2.2) is always closed and convex while may collapse to {0} at boundary points of closed sets, which in fact contradicts the very meaning of generalized normals. If Ω is convex, then both normal and prenormal cones reduce to the normal cone of convex analysis. In general we have 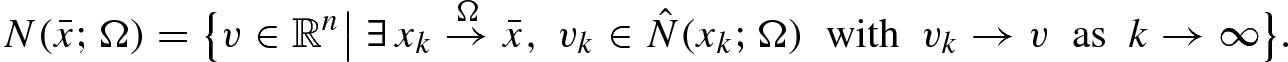
 as ε
k ↓ 0, where the latter expansions are defined by replacing 0 with ε
k on the right-hand side of (7.2.2).
as ε
k ↓ 0, where the latter expansions are defined by replacing 0 with ε
k on the right-hand side of (7.2.2). be a set-valued mapping/multifunction with values
be a set-valued mapping/multifunction with values  and with its domain and graph defined, respectively, by
and with its domain and graph defined, respectively, by 
 . Assuming that the graph of F is locally closed around
. Assuming that the graph of F is locally closed around  , we define the coderivative of F at this point via the normal cone (7.2.1) to the graph of F by
, we define the coderivative of F at this point via the normal cone (7.2.1) to the graph of F by 
 is a set-valued positively homogeneous mapping, which reduces to the adjoint/transposed Jacobian for all single-valued mappings
is a set-valued positively homogeneous mapping, which reduces to the adjoint/transposed Jacobian for all single-valued mappings  that are smooth around
that are smooth around  , where
, where  is dropped in this case in the coderivative notation:
is dropped in this case in the coderivative notation: 
 around
around  defined as follows: there exist neighborhoods U of
defined as follows: there exist neighborhoods U of  and V of
and V of  and a constant ℓ ≥ 0 such that
and a constant ℓ ≥ 0 such that 
 stands for the closed unit ball of the space in question. If
stands for the closed unit ball of the space in question. If  in (7.2.5), then it reduces to the classical local Lipschitzian property of F around
in (7.2.5), then it reduces to the classical local Lipschitzian property of F around  . The coderivative characterization of (7.2.5), which is called in [40] the Mordukhovich criterion, tells us that F is Lipschitz-like around
. The coderivative characterization of (7.2.5), which is called in [40] the Mordukhovich criterion, tells us that F is Lipschitz-like around  if and only if we have
if and only if we have 
 of the positively homogeneous coderivative mapping
of the positively homogeneous coderivative mapping  . The reader can find in [28–30, 40] different proofs of this result with numerous applications.
. The reader can find in [28–30, 40] different proofs of this result with numerous applications.![$$\varphi \colon \mathbb {R}^n\to \overline {\mathbb {R}}:=(-\infty ,\infty ]$$](../images/480569_1_En_7_Chapter/480569_1_En_7_Chapter_TeX_IEq31.png) finite at
finite at  and lower semicontinuous (l.s.c.) around this point. Denote by
and lower semicontinuous (l.s.c.) around this point. Denote by 
 and using the normal cone (7.2.1) to the epigraph of φ at
and using the normal cone (7.2.1) to the epigraph of φ at  , we define the two types of the subdifferentials of φ at
, we define the two types of the subdifferentials of φ at  : the basic subdifferential and the singular subdifferential by, respectively,
: the basic subdifferential and the singular subdifferential by, respectively, 

 for smooth functions and to the subdifferential of convex analysis if φ is convex. Observe that
for smooth functions and to the subdifferential of convex analysis if φ is convex. Observe that  and
and  via the coderivative (7.2.4) of the epigraphical multifunction
via the coderivative (7.2.4) of the epigraphical multifunction  defined by
defined by  . Thus the coderivative characterization (7.2.6) of the Lipschitz-like property of multifunctions implies that a lower semicontinuous function φ is locally Lipschitzian around
. Thus the coderivative characterization (7.2.6) of the Lipschitz-like property of multifunctions implies that a lower semicontinuous function φ is locally Lipschitzian around  if and only if
if and only if 
 with its indicator functionδ(x; Ω) = δ
Ω(x) equal 0 for x ∈ Ω and ∞ otherwise, we have that
with its indicator functionδ(x; Ω) = δ
Ω(x) equal 0 for x ∈ Ω and ∞ otherwise, we have that 

 . Namely, we have
. Namely, we have 
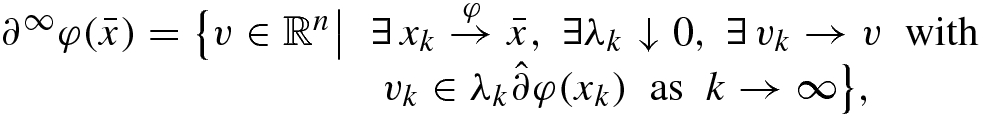
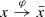 indicates that
indicates that  with
with  . Note that the presubdifferential (7.2.11) is related to the prenormal cone (7.2.2) as in (7.2.7) and is also used in variational analysis under the names of the Fréchet subdifferential and the viscosity subdifferential. Similarly to the case of basic normals in (7.2.3) it is not hard to observe that we still have the subdifferential representations in (7.2.12) and (7.2.13) if the presubdifferential (7.2.11) therein is expanded by its ε
k-enlargements
. Note that the presubdifferential (7.2.11) is related to the prenormal cone (7.2.2) as in (7.2.7) and is also used in variational analysis under the names of the Fréchet subdifferential and the viscosity subdifferential. Similarly to the case of basic normals in (7.2.3) it is not hard to observe that we still have the subdifferential representations in (7.2.12) and (7.2.13) if the presubdifferential (7.2.11) therein is expanded by its ε
k-enlargements
 defined with replacing 0 on the right-hand side of (7.2.11) by − ε
k.
defined with replacing 0 on the right-hand side of (7.2.11) by − ε
k.7.3 Extremal Principle in Variational Analysis
In this section we recall, following [22], the notion of locally extremal points for systems of finitely many sets and then derive the fundamental extremal principle, which gives us necessary conditions for extremality of closed set systems in  .
.
 , which are assumed to be locally closed around their common point
, which are assumed to be locally closed around their common point  . We say that
. We say that  is a Locally Extremal Point of the set system { Ω1, …, Ωs} if there exist a neighborhood U of
is a Locally Extremal Point of the set system { Ω1, …, Ωs} if there exist a neighborhood U of  and sequences of vectors
and sequences of vectors  , such that a
ik → 0 as k →∞ for all i ∈{1, …, s} and
, such that a
ik → 0 as k →∞ for all i ∈{1, …, s} and 
△
Geometrically Definition 7.3.1 says that  is a locally extremal point of the set system { Ω1, …, Ωs} if these sets can be pushed apart from each other locally around
is a locally extremal point of the set system { Ω1, …, Ωs} if these sets can be pushed apart from each other locally around  . Observe also that for the case of two sets Ω1, Ω2 containing
. Observe also that for the case of two sets Ω1, Ω2 containing  the above definition can be equivalently reformulated as follows: there is a neighborhood U of
the above definition can be equivalently reformulated as follows: there is a neighborhood U of  such that for any ε > 0 there exists a vector
such that for any ε > 0 there exists a vector  with ∥a∥≤ ε and ( Ω1 − a) ∩ Ω2 ∩ U = ∅.
with ∥a∥≤ ε and ( Ω1 − a) ∩ Ω2 ∩ U = ∅.
 , we have that
, we have that  is a locally extremal point of the set system
is a locally extremal point of the set system  . Furthermore, the introduced notion of set extremality covers various notions of optimality and equilibria in problems of scalar and vector optimization. In particular, a local minimizer
. Furthermore, the introduced notion of set extremality covers various notions of optimality and equilibria in problems of scalar and vector optimization. In particular, a local minimizer  of the general constrained optimization problem
of the general constrained optimization problem 
 , corresponds to the locally extremal point
, corresponds to the locally extremal point  of the sets Ω1 := epi φ and
of the sets Ω1 := epi φ and  . As we see below, extremal systems naturally arise in deriving calculus rules of generalized differentiation.
. As we see below, extremal systems naturally arise in deriving calculus rules of generalized differentiation.Now we are ready to formulate and prove the basic extremal principle of variational analysis for systems of finitely many closed sets in  by using the normal cone construction (7.2.1).
by using the normal cone construction (7.2.1).
 be a locally extremal point of the system { Ω
1, …, Ω
s} of nonempty subsets of
be a locally extremal point of the system { Ω
1, …, Ω
s} of nonempty subsets of
 , which are locally closed around
, which are locally closed around
 . Then there exist generalized normals
. Then there exist generalized normals
 for i = 1, …, s, not equal to zero simultaneously, such that we have the generalized Euler equation
for i = 1, …, s, not equal to zero simultaneously, such that we have the generalized Euler equation

△
 . Taking the sequences {a
ik} therein, for each k = 1, 2, … consider the unconstrained optimization problem:
. Taking the sequences {a
ik} therein, for each k = 1, 2, … consider the unconstrained optimization problem: ![$$\displaystyle \begin{aligned} \mbox{minimize }\;\varphi_k(x):=\Big[\sum_{i=1}^s d^2(x+a_{ik};\Omega _i)\Big]^{1/2}+\|x-\bar{x}\|{}^2,\quad x\in\mathbb{R}^n, \end{aligned} $$](../images/480569_1_En_7_Chapter/480569_1_En_7_Chapter_TeX_Equ16.png)
![$$\displaystyle \begin{aligned} \gamma_k:=\Big[\sum_{i=1}^sd^2(x_k+a_{ik};\Omega _i)\Big]^{1/2}>0. \end{aligned} $$](../images/480569_1_En_7_Chapter/480569_1_En_7_Chapter_TeX_Equ17.png)
![$$\displaystyle \begin{aligned} 0<\gamma_k+\|x_k-\bar{x}\|{}^2=\varphi_k(x_k)\le\varphi_k(\bar{x})=\Big[\sum_{i=1}^s\|a_{ik}\|{}^2\Big]^{1/2}\downarrow 0, \end{aligned}$$](../images/480569_1_En_7_Chapter/480569_1_En_7_Chapter_TeX_Equf.png)
 as k →∞. By the closedness of the sets Ωi, i = 1, …, s, around
as k →∞. By the closedness of the sets Ωi, i = 1, …, s, around  , we pick w
ik ∈ Π(x
k + a
ik; Ωi) and for each k form another unconstrained optimization problem:
, we pick w
ik ∈ Π(x
k + a
ik; Ωi) and for each k form another unconstrained optimization problem: ![$$\displaystyle \begin{aligned} \mbox{minimize }\;\psi_k(x):=\Big[\sum_{i=1}^s\|x+a_{ik}-w_{ik}\|{}^2\Big]^{1/2}+\|x-\bar{x}\|{}^2,\quad x\in\mathbb{R}^n \end{aligned} $$](../images/480569_1_En_7_Chapter/480569_1_En_7_Chapter_TeX_Equ18.png)


 , we get by passing to the limit as k →∞ in (7.3.6) and (7.3.7) that there exist v
1, …, v
s, not equal to zero simultaneously, for which (7.3.2) holds. Finally, it follows directly from the above constructions and the normal cone definition (7.2.1) that
, we get by passing to the limit as k →∞ in (7.3.6) and (7.3.7) that there exist v
1, …, v
s, not equal to zero simultaneously, for which (7.3.2) holds. Finally, it follows directly from the above constructions and the normal cone definition (7.2.1) that  for all i = 1, …, s. This completes the proof of the theorem. □
for all i = 1, …, s. This completes the proof of the theorem. □7.4 Fundamental Calculus Rules
Employing the extremal principle, we derive here two fundamental rules of generalized differential calculus, which are broadly used in this chapter and from which many other calculus rules follow; see [29, 30]. The first result is the intersection rule for basic normals (7.2.1).
 , which are locally closed around their common point
, which are locally closed around their common point
 . Assume the validity of the following qualification condition:
. Assume the validity of the following qualification condition:
![$$\displaystyle \begin{aligned} \big[x_i\in N(\bar{x};\Omega _i),\;x_1+\ldots+x_s=0\big]\Longrightarrow x_i=0\;\mathit{\mbox{ for all }}\;i=1,\ldots,s. \end{aligned} $$](../images/480569_1_En_7_Chapter/480569_1_En_7_Chapter_TeX_Equ21.png)

△
 and use the normal cone representation (7.2.3). It gives us sequences
and use the normal cone representation (7.2.3). It gives us sequences  with x
k ∈ Ω1 ∩ Ω2 and v
k → v with
with x
k ∈ Ω1 ∩ Ω2 and v
k → v with  as k →∞. Take any sequence ε
k ↓ 0 and construct the sets
as k →∞. Take any sequence ε
k ↓ 0 and construct the sets 

 for which
for which 
 with ∥(u, λ)∥ = 1. Passing to the limit in the first inclusion of (7.4.3) gives us
with ∥(u, λ)∥ = 1. Passing to the limit in the first inclusion of (7.4.3) gives us  , which immediately implies—by the easily verifiable product rule equality for normals to Cartesian products (see, e.g., [29, Proposition 1.2])—that
, which immediately implies—by the easily verifiable product rule equality for normals to Cartesian products (see, e.g., [29, Proposition 1.2])—that  and λ ≤ 0. On the other hand, the limiting procedure in the second inclusion of (7.4.3) leads us by the structure of Θ2k to
and λ ≤ 0. On the other hand, the limiting procedure in the second inclusion of (7.4.3) leads us by the structure of Θ2k to 
 rewrite the set Θ2k as
rewrite the set Θ2k as 
 we find sequences x
km → x
k, α
km ↓ 0, u
km → u
k and λ
km → λ
k as m →∞ such that
we find sequences x
km → x
k, α
km ↓ 0, u
km → u
k and λ
km → λ
k as m →∞ such that 
 The latter means by definition (7.2.2) of regular normals that
The latter means by definition (7.2.2) of regular normals that 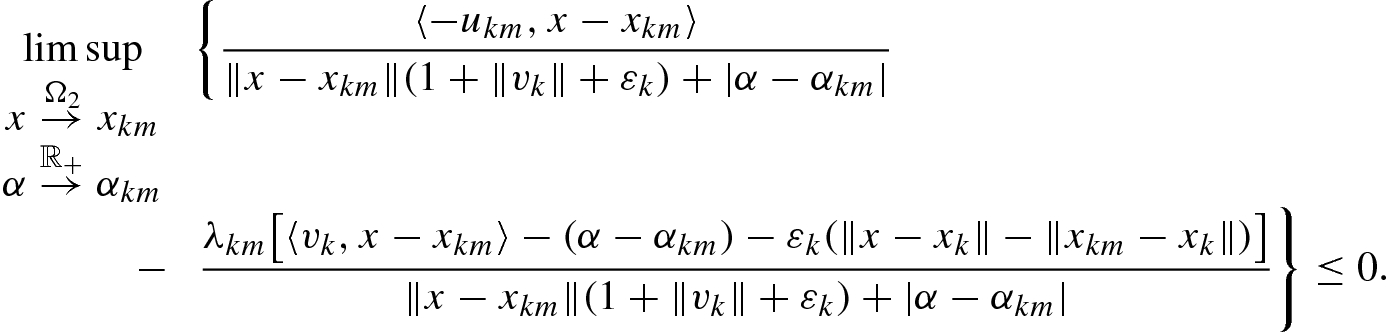
 and
and  we arrive at the limiting condition
we arrive at the limiting condition 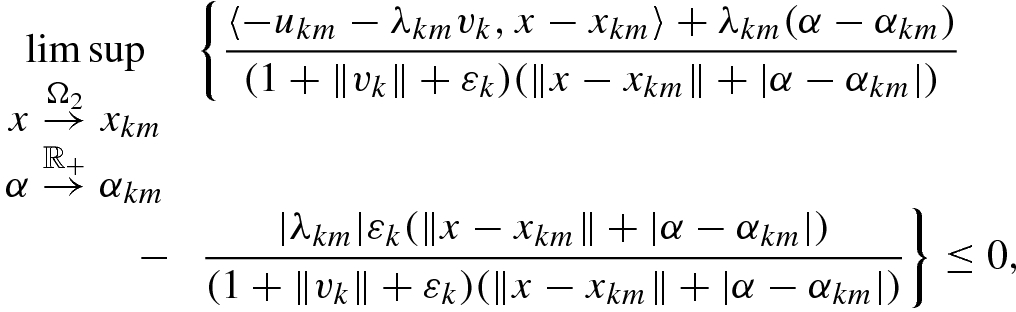

Observe that having λ = 0 in (7.4.4) contradicts the qualification condition (7.4.1) for s = 2. Thus λ < 0, which readily implies that  .
.
To proceed finally by induction for s > 2, we observe that the induction assumption for (7.4.2) in the previous step yields the validity of the qualification condition (7.4.1) needed for the current step of induction. This completes the proof of the theorem. □
Next we derive the subdifferential sum rules concerning both basic subdifferential (7.2.7) and singular subdifferential (7.2.8). For our subsequent applications to bilevel optimization, it is sufficient to consider the case where all but one of the functions involved in summation are locally Lipschitzian around the reference point. This case allows us to obtain the subdifferential sum rules without any qualification conditions.
 be l.s.c. around
be l.s.c. around
 , and let
, and let
 for i = 2, …, s and s ≥ 2 be locally Lipschitzian around
for i = 2, …, s and s ≥ 2 be locally Lipschitzian around
 . Then we have the sum rules
. Then we have the sum rules


△
We consider the case where only two functions are under summation since the general case of finitely many functions obviously follows by induction. Let us start with the basic subdifferential sum rule (7.4.5) for s = 2 therein.
 and get by definition (7.2.7) that
and get by definition (7.2.7) that 

 , we obviously have that the sets Ω1 and Ω2 are locally closed around the triple
, we obviously have that the sets Ω1 and Ω2 are locally closed around the triple  . It is easy to check that
. It is easy to check that  . Applying now to this set intersection the normal cone intersection rule from Theorem 7.4.1, we observe that the qualification condition (7.4.1) is automatically satisfied in this case due to the singular subdifferential characterization (7.2.9) of the local Lipschitz continuity. Hence we get pairs
. Applying now to this set intersection the normal cone intersection rule from Theorem 7.4.1, we observe that the qualification condition (7.4.1) is automatically satisfied in this case due to the singular subdifferential characterization (7.2.9) of the local Lipschitz continuity. Hence we get pairs  for i = 1, 2 satisfying the condition
for i = 1, 2 satisfying the condition 
 for i = 1, 2, and thus the sum rule (7.4.5) is verified.
for i = 1, 2, and thus the sum rule (7.4.5) is verified. and find by definition sequences
and find by definition sequences 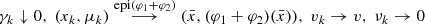 , and η
k ↓ 0 such that
, and η
k ↓ 0 such that 
 and |μ − μ
k|≤ η
k as k = 1, 2, …. Taking a Lipschitz constant ℓ > 0 of φ
2 around
and |μ − μ
k|≤ η
k as k = 1, 2, …. Taking a Lipschitz constant ℓ > 0 of φ
2 around  , denote
, denote  and
and  . Then
. Then 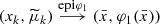 and
and 
 , and
, and  . Therefore
. Therefore 
 and
and  . It yields
. It yields  for all k = 1, 2, …, and so
for all k = 1, 2, …, and so  since ε
k ↓ 0 as k →∞. This verifies the inclusion “⊂” in (7.4.6). Applying it to the sum φ
1 = (φ
1 + φ
2) + (−φ
2) yields
since ε
k ↓ 0 as k →∞. This verifies the inclusion “⊂” in (7.4.6). Applying it to the sum φ
1 = (φ
1 + φ
2) + (−φ
2) yields  , which justifies the equality in (7.4.6) and thus completes the proof. □
, which justifies the equality in (7.4.6) and thus completes the proof. □7.5 Subdifferentials and Lipschitz Continuity of Value Functions
 defined by
defined by 
 is an l.s.c. function, and where
is an l.s.c. function, and where  is a set-valued mapping of closed graph. We can view (7.5.1) as the optimal value function in the problem of parametric optimization described as follows:
is a set-valued mapping of closed graph. We can view (7.5.1) as the optimal value function in the problem of parametric optimization described as follows: 
As seen below, functions of type (7.5.1) play a crucial role in applications to bilevel optimization while revealing intrinsic nonsmoothness of the latter class of optimization problems. This section presents evaluations of both basic and singular subdifferentials of (7.5.1), which are equally important for the aforementioned applications. Singular subdifferential evaluations are used for establishing the Lipschitz continuity of 𝜗(x) with respect to the parameter x that allows us to reduce the bilevel model under consideration to a single-level problem of Lipschitzian programming. On the other hand, basic subdifferential evaluations open the gate to derive in this way necessary optimality conditions for Lipschitzian bilevel programs.
 associated with (7.5.1) by
associated with (7.5.1) by 
 if for every sequence
if for every sequence 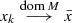 there exists a sequence y
k ∈ M(x
k) that converges to
there exists a sequence y
k ∈ M(x
k) that converges to  as k →∞. Observe that the inner semicontinuity of M at
as k →∞. Observe that the inner semicontinuity of M at  is implied by its Lipschitz-like property at this point.
is implied by its Lipschitz-like property at this point.The following theorem gives us efficient upper estimates of both basic and singular subdifferentials of the optimal value function 𝜗 needed for subsequent applications. We confine ourselves to the case of local Lipschitz continuity of the cost function φ in (7.5.1) that is sufficient to derive necessary optimality conditions for bilevel programs in Sects. 7.8 and 7.9.
 , and let the cost function φ be locally Lipschitzian around this point. Then we have
, and let the cost function φ be locally Lipschitzian around this point. Then we have
![$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \partial\vartheta(\bar{x})\subset\bigcup_{(v,w)\in\partial\varphi(\bar{x},\bar{y})}\Big[v+D^*F(\bar{x},\bar{y})(w)\Big], \end{array} \end{aligned} $$](../images/480569_1_En_7_Chapter/480569_1_En_7_Chapter_TeX_Equ31.png)

△
 defined via the indicator function of the set gph F by
defined via the indicator function of the set gph F by 

 and get from its representation in (7.2.12) sequences
and get from its representation in (7.2.12) sequences 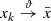 and v
k → v with
and v
k → v with  as k →∞. Based on definition (7.2.11), for any sequence ε
k ↓ 0 there exists η
k ↓ 0 as k →∞ such that
as k →∞. Based on definition (7.2.11), for any sequence ε
k ↓ 0 there exists η
k ↓ 0 as k →∞ such that 

 . This tells us that
. This tells us that  for all k = 1, 2, …. Employing further the inner semicontinuity of the argminimum mapping M at
for all k = 1, 2, …. Employing further the inner semicontinuity of the argminimum mapping M at  , we find a sequence of y
k ∈ M(x
k) converging to
, we find a sequence of y
k ∈ M(x
k) converging to  as k →∞. It follows from imposed convergence
as k →∞. It follows from imposed convergence  that
that  . Hence we arrive at
. Hence we arrive at  by passing to the limit as k →∞, which verifies therefore the validity of the upper estimate (7.5.6). To derive from (7.5.6) the one in (7.5.3) claimed in the theorem, it remains to use in (7.5.6) the basic subdifferential sum rule (7.4.5) from Theorem 7.4.2 combining it with subdifferentiation of the indicator function in (7.2.10) and the coderivative definition in (7.2.4).
by passing to the limit as k →∞, which verifies therefore the validity of the upper estimate (7.5.6). To derive from (7.5.6) the one in (7.5.3) claimed in the theorem, it remains to use in (7.5.6) the basic subdifferential sum rule (7.4.5) from Theorem 7.4.2 combining it with subdifferentiation of the indicator function in (7.2.10) and the coderivative definition in (7.2.4).
 and taking any sequence ε
k ↓ 0, find by (7.2.13) sequences
and taking any sequence ε
k ↓ 0, find by (7.2.13) sequences 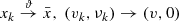 , and η
k ↓ 0 as k →∞ satisfying
, and η
k ↓ 0 as k →∞ satisfying 
 , and |μ − μ
k|≤ η
k. The assumed inner semicontinuity of (7.5.2) ensures the existence of sequences
, and |μ − μ
k|≤ η
k. The assumed inner semicontinuity of (7.5.2) ensures the existence of sequences 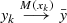 and
and  such that
such that 
 of the prenormal cone to the epigraph of ψ. This gives us (7.5.7) by passing to the limit as k →∞. Applying finally to ∂
∞ψ in (7.5.7) the singular subdifferential relation (7.4.6) from Theorem 7.4.2 with taking into account the singular subdifferential calculation in (7.2.10) together with the coderivative definition (7.2.4), we arrive at the claimed upper estimate (7.5.4) and thus complete the proof of the theorem. □
of the prenormal cone to the epigraph of ψ. This gives us (7.5.7) by passing to the limit as k →∞. Applying finally to ∂
∞ψ in (7.5.7) the singular subdifferential relation (7.4.6) from Theorem 7.4.2 with taking into account the singular subdifferential calculation in (7.2.10) together with the coderivative definition (7.2.4), we arrive at the claimed upper estimate (7.5.4) and thus complete the proof of the theorem. □As mentioned above, in our applications to bilevel programming we need to have verifiable conditions that ensure the local Lipschitz continuity of the optimal value function (7.5.1). This is provided by the following corollary, which is a direct consequence of Theorem 7.5.1 and the coderivative criterion (7.2.6) for the Lipschitz-like property.
In addition to the assumptions of Theorem
7.5.1, suppose that the constraint mapping F is Lipschitz-like around
 in (7.5.2). Then the optimal value function (7.5.1) is locally Lipschitzian around
in (7.5.2). Then the optimal value function (7.5.1) is locally Lipschitzian around
 . △
. △
We know from the coderivative criterion (7.2.6) that F is Lipschitz-like around  if and only if
if and only if  . Applying it to (7.5.4) tells us that the assumed Lipschitz-like property of the constraint mapping F in (7.5.1) ensures that
. Applying it to (7.5.4) tells us that the assumed Lipschitz-like property of the constraint mapping F in (7.5.1) ensures that  . Furthermore, it easily follows from the assumptions made that the optimal value function is l.s.c. around
. Furthermore, it easily follows from the assumptions made that the optimal value function is l.s.c. around  . Thus 𝜗 is locally Lipschitzian around
. Thus 𝜗 is locally Lipschitzian around  by the characterization of this property given in (7.2.9). □
by the characterization of this property given in (7.2.9). □
7.6 Problems of Lipschitzian Programming
Before deriving necessary optimality conditions in Lipschitzian problems of bilevel optimization in the subsequent sections, we devote this section to problems of single-level Lipschitzian programming. The results obtained here are based on the extremal principle and subdifferential characterization of local Lipschitzian functions while being instrumental for applications to bilevel programs given in Sect. 7.8.

 , are locally Lipschitzian around the reference point
, are locally Lipschitzian around the reference point  . The next theorem provides necessary optimality conditions in problem (7.6.1) of Lipschitzian programming that are expressed in terms of the basic subdifferential (7.2.7).
. The next theorem provides necessary optimality conditions in problem (7.6.1) of Lipschitzian programming that are expressed in terms of the basic subdifferential (7.2.7). be a feasible solution to problem (7.6.1) that gives a local minimum to the cost function φ
0therein. Then there exist multipliers λ
0, …, λ
msatisfying the sign conditions
be a feasible solution to problem (7.6.1) that gives a local minimum to the cost function φ
0therein. Then there exist multipliers λ
0, …, λ
msatisfying the sign conditions




![$$\displaystyle \begin{aligned} \Big[\displaystyle\sum_{i\in I(\bar{x})}\lambda_i v_i=0,\;\lambda_i\ge 0\Big]\Longrightarrow\Big[\lambda_i=0\;\mathit{\mbox{ for all }}\;i\in I(\bar{x})\Big] \end{aligned} $$](../images/480569_1_En_7_Chapter/480569_1_En_7_Chapter_TeX_Equ41.png)
whenever
 with
with
 . Then the necessary optimality conditions formulated above hold with λ
0 = 1. △
. Then the necessary optimality conditions formulated above hold with λ
0 = 1. △
 , consider the point
, consider the point  and form the following system of m + 2 sets in the space
and form the following system of m + 2 sets in the space  :
: 

 and that all the sets Ωi, i = 0, …, m + 1, are locally closed around
and that all the sets Ωi, i = 0, …, m + 1, are locally closed around  . Furthermore, there exists a neighborhood U of the local minimizer
. Furthermore, there exists a neighborhood U of the local minimizer  such that for any ε > 0 we find ν ∈ (0, ε) ensuring that
such that for any ε > 0 we find ν ∈ (0, ε) ensuring that 
 with
with  standing at the first position after
standing at the first position after  . Indeed, the negation of (7.6.8) contradicts the local minimality of
. Indeed, the negation of (7.6.8) contradicts the local minimality of  in (7.6.1). Having (7.6.8) gives us (7.3.1) for the set system in (7.6.7a), (7.6.7b) and thus verifies that
in (7.6.1). Having (7.6.8) gives us (7.3.1) for the set system in (7.6.7a), (7.6.7b) and thus verifies that  is a locally extremal point of these sets. Applying now the extremal principle from Theorem 7.3.2 to { Ω0, …, Ωm+1} at
is a locally extremal point of these sets. Applying now the extremal principle from Theorem 7.3.2 to { Ω0, …, Ωm+1} at  with taking into account the structures of Ωi, we get
with taking into account the structures of Ωi, we get  , and
, and  satisfying the inclusions
satisfying the inclusions 



To check further the complementary slackness conditions in (7.6.4), fix i ∈{1, …, m} and suppose that  . Then the continuity of φ
i at
. Then the continuity of φ
i at  ensures that the pair
ensures that the pair  is an interior point of the epigraphical set epi φ
i. It readily implies that
is an interior point of the epigraphical set epi φ
i. It readily implies that  , and hence λ
i = 0. This yields
, and hence λ
i = 0. This yields  , which justifies (7.6.4).
, which justifies (7.6.4).
To complete the proof of the theorem, it remains to check that the validity of (7.6.6) ensures that λ 0 = 1 in (7.6.5). We easily arrive at this assertion while arguing by contradiction. □
If the constraint functions φ
i, i = 1, …, m, are smooth around the reference point  , condition (7.6.6) clearly reduces to the classical Mangasarian-Fromovitz constraint qualification. It suggests us to label this condition (7.6.6) as the generalized Mangasarian-Fromovitz constraint qualification, or the generalized MFCQ.
, condition (7.6.6) clearly reduces to the classical Mangasarian-Fromovitz constraint qualification. It suggests us to label this condition (7.6.6) as the generalized Mangasarian-Fromovitz constraint qualification, or the generalized MFCQ.
7.7 Variational Approach to Bilevel Optimization
This section is devoted to describing some models of bilevel programming and a variational approach to them that involves nondifferentiable optimal value functions in single-level problems of parametric optimization.
 under each fixed parameter
under each fixed parameter  :
: 
 is the cost function and
is the cost function and  is the constraint mapping in (7.7.1), which is called the lower-level problem of parametric optimization. Denoting by
is the constraint mapping in (7.7.1), which is called the lower-level problem of parametric optimization. Denoting by 
 and given yet another cost function
and given yet another cost function  , we consider the upper-level parametric optimization problem of minimizing ψ(x, y) over the lower-level solution map
, we consider the upper-level parametric optimization problem of minimizing ψ(x, y) over the lower-level solution map  from (7.7.2) written as:
from (7.7.2) written as: 

 be a given constraint set. On the other hand, the pessimistic bilevel programming model is defined as follows:
be a given constraint set. On the other hand, the pessimistic bilevel programming model is defined as follows: 
The main attention in this and subsequent sections is paid to the application of the machinery and results of variational analysis and generalized differentiation to problems of bilevel optimization by implementing the value function approach. This approach is based on reducing bilevel programs to single-level problems of mathematical programming by using the nonsmooth optimal value function𝜗(x) of the lower-level problem defined in (7.5.1). Such a device was initiated by Outrata [35] for a particular class of bilevel optimization problems and was used by him for developing a numerical algorithm to solve bilevel programs. Then this approach was strongly developed by Ye and Zhu [44] who employed it to derive necessary optimality conditions for optimistic bilevel programs by using Clarke’s generalized gradients of optimal value functions. More advanced necessary optimality conditions for optimistic bilevel programs in terms of the author’s generalized differentiation reviewed in Sect. 7.2 were developed in [11, 12, 30, 34, 46, 47]. Optimality and stability conditions for pessimistic bilevel models were derived in [13, 16].
We restrict ourselves in what follows to implementing variational analysis and the aforementioned machinery of generalized differentiation within the value function approach to optimistic bilevel models with Lipschitzian data in finite-dimensional spaces. This allows us to most clearly communicate the basic variational ideas behind this approach, without additional technical complications. The variational results presented in the previous sections make our presentation self-contained and complete.


7.8 Optimality Conditions for Lipschitzian Bilevel Programs



There are various efficient conditions, which ensure the fulfillment of the partial calmness property for (7.8.2). They include the uniform sharp minimum condition [44], linearity of the lower-level problem with respect to the decision variable [9], the kernel condition [30], etc. On the other hand, partial calmness may fail in rather common situations; see [19, 30] for more results and discussions on partial calmness and related properties.
The main impact of partial calmness to deriving necessary optimality conditions for (7.8.2) is its equivalence to the possibility of transferring the troublesome constraint φ(x, y) ≤ 𝜗(x) into the penalized cost function as in the following proposition.
 with ψ being continuous at this point. Then
with ψ being continuous at this point. Then
 is a local optimal solution to the penalized problem
is a local optimal solution to the penalized problem

where the number κ > 0 is taken from (7.8.4). △
 , we find γ > 0 and η > 0 with
, we find γ > 0 and η > 0 with ![$$\tilde U:=[(\bar {x},\bar {y})+\eta \mathbb {B}]\times (-\gamma ,\gamma )\subset U$$](../images/480569_1_En_7_Chapter/480569_1_En_7_Chapter_TeX_IEq187.png) and
and 

![$$(x,y)\in [(\bar {x},\bar {y})+\eta \mathbb {B}]\cap \mbox{gph}\, F$$](../images/480569_1_En_7_Chapter/480569_1_En_7_Chapter_TeX_IEq188.png) with F taken from (7.7.6). If
with F taken from (7.7.6). If  , then (7.8.6) follows from (7.8.4). In the remaining case where
, then (7.8.6) follows from (7.8.4). In the remaining case where  , we get that
, we get that 
 . The feasibility of
. The feasibility of  to (7.8.2) tells us that
to (7.8.2) tells us that  , which thus verifies the claimed statement. □
, which thus verifies the claimed statement. □Thus the imposed partial calmness allows us to deduce the original problem of optimistic bilevel optimization to the single-level mathematical program (7.8.5) with conventional inequality constraints, where the troublesome term φ(x, y) − 𝜗(x) enters the penalized cost function. To derive necessary optimality conditions for (7.8.5), let us reformulate the generalized MFCQ (7.6.6) in conventional bilevel terms as in the case of bilevel programs with smooth data [6].
 is lower-level regular if it satisfies the generalized MFCQ in the lower-level problem (7.7.1). This means due to the structure of (7.7.1) that
is lower-level regular if it satisfies the generalized MFCQ in the lower-level problem (7.7.1). This means due to the structure of (7.7.1) that ![$$\displaystyle \begin{aligned} \Big[\displaystyle\sum_{i\in I(\bar{x},\bar{y})}\lambda_i v_i=0,\;\lambda_i\ge 0\Big]\Longrightarrow\Big[\lambda_i=0\;\mbox{ for all }\;i\in I(\bar{x},\bar{y})\Big] \end{aligned} $$](../images/480569_1_En_7_Chapter/480569_1_En_7_Chapter_TeX_Equ63.png)
 with some
with some  and
and 
 satisfying the upper-level constraints in (7.7.7) is upper-level regular if
satisfying the upper-level constraints in (7.7.7) is upper-level regular if ![$$\displaystyle \begin{aligned} \Big[\displaystyle 0\in\sum_{j\in J(\bar{x})}\mu_j\partial g_j(\bar{x}),\;\mu_j\ge 0\Big]\Longrightarrow\Big[\mu_j=0\;\mbox{ whenever }\;j\in J(\bar{x})\Big] \end{aligned} $$](../images/480569_1_En_7_Chapter/480569_1_En_7_Chapter_TeX_Equ64.png)
 .
.Now we are ready for the application of Theorem 7.6.1 to the optimistic bilevel program in the equivalent form (7.8.5). To proceed, we have to verify first that the optimal value function 𝜗(x) in the cost function of (7.8.5) is locally Lipschitzian around the reference point and then to be able to upper estimate the basic subdifferential (7.2.7) of the function − 𝜗(⋅). Since the basic subdifferential  does not possess the plus-minus symmetry while its convex hull
does not possess the plus-minus symmetry while its convex hull  does, we need to convexify in the proof the set on the right-hand side of the upper estimate in (7.5.3). In this way we arrive at the following major result.
does, we need to convexify in the proof the set on the right-hand side of the upper estimate in (7.5.3). In this way we arrive at the following major result.
 be a local optimal solution to the optimistic bilevel program in the equivalent form (7.8.2) with the lower-level optimal value function 𝜗(x) defined in (7.8.1). Assume that all the functions φ, ψ, f
i, g
jare locally Lipschitzian around the reference point, that the lower-level solution map S from (7.7.2) is inner semicontinuous at
be a local optimal solution to the optimistic bilevel program in the equivalent form (7.8.2) with the lower-level optimal value function 𝜗(x) defined in (7.8.1). Assume that all the functions φ, ψ, f
i, g
jare locally Lipschitzian around the reference point, that the lower-level solution map S from (7.7.2) is inner semicontinuous at
 , that the lower-level regularity (7.8.7) and upper-level regularity (7.8.8) conditions hold, and that problem (7.8.2) is partially calm at
, that the lower-level regularity (7.8.7) and upper-level regularity (7.8.8) conditions hold, and that problem (7.8.2) is partially calm at
 with constant κ > 0. Then there exist multipliers λ
1, …, λ
r, μ
1, …, μ
s, and ν
1, …, ν
rsatisfying the sign and complementary slackness conditions
with constant κ > 0. Then there exist multipliers λ
1, …, λ
r, μ
1, …, μ
s, and ν
1, …, ν
rsatisfying the sign and complementary slackness conditions






△
 is a local minimizer of the mathematical program (7.8.5) with inequality constraints. To show that it belongs to problems of Lipschitzian programming considered in Sect. 7.6, we need to check that the optimal value function (7.8.1) is locally Lipschitzian around
is a local minimizer of the mathematical program (7.8.5) with inequality constraints. To show that it belongs to problems of Lipschitzian programming considered in Sect. 7.6, we need to check that the optimal value function (7.8.1) is locally Lipschitzian around  under the assumptions made. This function is clearly l.s.c. around
under the assumptions made. This function is clearly l.s.c. around  , and thus its Lipschitz continuity around this point is equivalent to the condition
, and thus its Lipschitz continuity around this point is equivalent to the condition  . It follows from the upper estimate (7.5.4) of Theorem 7.5.1 and the assumed inner semicontinuity of the solution map (7.7.2) at
. It follows from the upper estimate (7.5.4) of Theorem 7.5.1 and the assumed inner semicontinuity of the solution map (7.7.2) at  that
that 
 follows from the Lipschitz-like property of the mapping
follows from the Lipschitz-like property of the mapping  . Since
. Since 
 from the assumed lower-level regularity due to the coderivative definition and the normal come intersection rule in Theorem 7.4.1. Thus F is Lipschitz-like around
from the assumed lower-level regularity due to the coderivative definition and the normal come intersection rule in Theorem 7.4.1. Thus F is Lipschitz-like around  by the coderivative criterion (7.2.6), and the Lipschitz continuity of 𝜗(⋅) is verified.
by the coderivative criterion (7.2.6), and the Lipschitz continuity of 𝜗(⋅) is verified.
 in (7.8.14), recall that
in (7.8.14), recall that 
 stands for Clarke’s generalized gradient of locally Lipschitzian functions that possesses the plus-minus symmetry property [4]. Using it in (7.8.14), we get
stands for Clarke’s generalized gradient of locally Lipschitzian functions that possesses the plus-minus symmetry property [4]. Using it in (7.8.14), we get  such that
such that 
The next section presents an independent set of necessary optimality conditions for optimistic bilevel programs with Lipschitzian data that are obtained without using any convexification while employing instead yet another variational device and subdifferential calculus rule.
7.9 Bilevel Optimization via Subdifferential Difference Rule
Considering the single-level problem (7.8.5), which we are finally dealing with while deriving necessary optimality conditions for optimistic bilevel programs, note that the objective therein contains the difference of two nonsmooth functions. The basic subdifferential (7.2.7) does not possesses any special rule for difference of nonsmooth functions, but the regular subdifferential (7.2.11) does, as was first observed in [33] by using a smooth variational description of regular subgradients. Here we employ this approach to establish necessary optimality conditions for Lipschitzian bilevel programs that are different from those in Theorem 7.8.3.
The derivation of these necessary optimality conditions is based on the following two results, which are certainly of their independent interest. The first one provides a smooth variational description of regular subgradients of arbitrary functions  .
.
Let
 be finite at
be finite at
 , and let
, and let
 . Then there exists a neighborhood U of
. Then there exists a neighborhood U of
 and a function
and a function
 such that
such that
 , that ψ is Fréchet differentiable at
, that ψ is Fréchet differentiable at
 with
with
 , and that the difference ψ − φ achieves at
, and that the difference ψ − φ achieves at
 its local maximum on U. △
its local maximum on U. △

 if and only if there exists a neighborhood U of
if and only if there exists a neighborhood U of  and a function
and a function  such that ψ is Fréchet differentiable at
such that ψ is Fréchet differentiable at  with
with  while achieving at
while achieving at  its local maximum relative to Ω.
its local maximum relative to Ω. satisfying the listed properties we get
satisfying the listed properties we get 
 , and thus
, and thus  by definition (7.2.2). Conversely, pick
by definition (7.2.2). Conversely, pick  and define the function
and define the function 
The second lemma gives us the aforementioned difference rule for regular subgradients.
 that are finite at
that are finite at
 and assume that
and assume that
 . Then we have the inclusions
. Then we have the inclusions
![$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \hat\partial(\varphi_1-\varphi_2)(\bar{x})\subset\bigcap_{v\in\hat\partial\varphi_2(\bar{x})}\Big[\hat\partial\varphi_1(\bar{x})-v\Big]\subset \hat\partial\varphi_1(\bar{x})-\hat\partial\varphi_2(\bar{x}). \end{array} \end{aligned} $$](../images/480569_1_En_7_Chapter/480569_1_En_7_Chapter_TeX_Equ73.png)
 of the difference function φ
1 − φ
2satisfies the necessary optimality condition
of the difference function φ
1 − φ
2satisfies the necessary optimality condition

△
 . Then the smooth variational description of v from Lemma 7.9.1 gives us
. Then the smooth variational description of v from Lemma 7.9.1 gives us  on a neighborhood U of
on a neighborhood U of  that is differentiable at
that is differentiable at  with
with 
 and for any ε > 0 find γ > 0 such that
and for any ε > 0 find γ > 0 such that 
 . Due to the differentiability of ψ at
. Due to the differentiability of ψ at  we use the elementary sum rule for the regular subgradients (see, e.g., [29, Proposition 1.107(i)]) and immediately get the relationships
we use the elementary sum rule for the regular subgradients (see, e.g., [29, Proposition 1.107(i)]) and immediately get the relationships 
Now we are in a position to derive refined necessary optimality conditions for optimistic bilevel programs with Lipschitzian data.
 be a local optimal solution to the optimistic bilevel program in the equivalent form (7.8.2) without upper level constraints. Suppose that all the functions φ, ψ, f
iare locally Lipschitzian around the reference point, that the lower-level solution map S in (7.7.2) is inner semicontinuous at
be a local optimal solution to the optimistic bilevel program in the equivalent form (7.8.2) without upper level constraints. Suppose that all the functions φ, ψ, f
iare locally Lipschitzian around the reference point, that the lower-level solution map S in (7.7.2) is inner semicontinuous at
 , that the lower-level regularity (7.8.7) condition holds, and that problem (7.8.2) is partially calm at
, that the lower-level regularity (7.8.7) condition holds, and that problem (7.8.2) is partially calm at
 with constant κ > 0. Assume in addition that
with constant κ > 0. Assume in addition that
 for the optimal value function (7.8.1). Then there exists a vector
for the optimal value function (7.8.1). Then there exists a vector
 together with multipliers λ
1, …, λ
rand ν
1, …, ν
rfor i = 1, …, r satisfying the sign and complementary slackness conditions in (7.8.11) and (7.8.9), respectively, such that
together with multipliers λ
1, …, λ
rand ν
1, …, ν
rfor i = 1, …, r satisfying the sign and complementary slackness conditions in (7.8.11) and (7.8.9), respectively, such that


△
 a local minimizer for the unconstrained optimization problem
a local minimizer for the unconstrained optimization problem 
 defined in (7.7.6). Then applying to (7.9.5) the difference rule (7.9.2) from Proposition 7.9.2 gives us the inclusion
defined in (7.7.6). Then applying to (7.9.5) the difference rule (7.9.2) from Proposition 7.9.2 gives us the inclusion 

 by the larger ∂ on the right-hand sides of (7.9.6) and (7.9.7) and then using the basic subdifferential sum rule from Theorem 7.4.2 yield the inclusions
by the larger ∂ on the right-hand sides of (7.9.6) and (7.9.7) and then using the basic subdifferential sum rule from Theorem 7.4.2 yield the inclusions 
 with the usage of the singular subdifferential characterization of Lipschitzian functions in (7.2.9), we get
with the usage of the singular subdifferential characterization of Lipschitzian functions in (7.2.9), we get 
 ensuring the validity of (7.9.3) and
ensuring the validity of (7.9.3) and 
Observe that we always have  if the optimal value function (7.8.1) is convex, which is surely the case when all the functions φ and f
i therein are convex. If in addition the upper-level data are also convex, more general results were derived in [17] for problems of semi-infinite programming with arbitrary number of inequality constraints in locally convex topological vector spaces by reducing them to problems of DC programming with objectives represented as differences of convex functions. Note further that the necessary optimality conditions obtained in Theorems 7.8.3 and 7.9.3 are independent of each other even in the case of bilevel programs with smooth data. In particular, we refer the reader to [30, Example 6.24] for illustrating this statement and for using the obtained results to solve smooth bilevel programs. Finally, we mention the possibility to replace the inner semicontinuity assumption on the solution map S(x) imposed in both Theorems 7.8.3 and 7.9.3 by the uniform boundedness of this map in finite-dimensions, or by its inner semicompactness counterpart in infinite-dimensional spaces; cf. [11, 16, 30, 34] for similar transitions in various bilevel settings.
if the optimal value function (7.8.1) is convex, which is surely the case when all the functions φ and f
i therein are convex. If in addition the upper-level data are also convex, more general results were derived in [17] for problems of semi-infinite programming with arbitrary number of inequality constraints in locally convex topological vector spaces by reducing them to problems of DC programming with objectives represented as differences of convex functions. Note further that the necessary optimality conditions obtained in Theorems 7.8.3 and 7.9.3 are independent of each other even in the case of bilevel programs with smooth data. In particular, we refer the reader to [30, Example 6.24] for illustrating this statement and for using the obtained results to solve smooth bilevel programs. Finally, we mention the possibility to replace the inner semicontinuity assumption on the solution map S(x) imposed in both Theorems 7.8.3 and 7.9.3 by the uniform boundedness of this map in finite-dimensions, or by its inner semicompactness counterpart in infinite-dimensional spaces; cf. [11, 16, 30, 34] for similar transitions in various bilevel settings.
7.10 Concluding Remarks and Open Questions
In this self-contained chapter of the book we described a variational approach to bilevel optimization with its implementation to deriving advanced necessary optimality conditions for optimistic bilevel programs in finite-dimensional spaces. The entire machinery of variational analysis and generalized differentiation (including the fundamental extremal principle, major calculus rules, and subdifferentiation of optimal value functions), which is needed for this device, is presented here with the proofs. The given variational approach definitely has strong perspectives for further developments. Let us briefly discuss some open questions in this direction.
The major difference between the optimistic model (7.7.4) and pessimistic model (7.7.5) in bilevel programming is that the latter invokes the supremum marginal/optimal value function instead of the infimum type in (7.7.4). Subdifferentiation of the supremum marginal functions is more involved in comparison with that of the infimum type. Some results in this vein for problems with Lipschitzian data can be distilled from the recent papers [31, 32, 38], while their implementation in the framework of pessimistic bilevel programs is a challenging issue.
The given proof of the necessary optimality conditions for bilevel programs in Theorem 7.8.3 requires an upper estimate of
 , which cannot be directly derived from that for
, which cannot be directly derived from that for  since
since  . To obtain such an estimate, we used the subdifferential convexification and the fact that the convexified/Clarke subdifferential of Lipschitz continuous functions possesses the plus-minus symmetry. However, there is a nonconvex subgradient set that is much smaller than Clarke’s one while having this symmetry. It is the symmetric subdifferential
. To obtain such an estimate, we used the subdifferential convexification and the fact that the convexified/Clarke subdifferential of Lipschitz continuous functions possesses the plus-minus symmetry. However, there is a nonconvex subgradient set that is much smaller than Clarke’s one while having this symmetry. It is the symmetric subdifferential
 , which enjoys full calculus induced by the basic one. Efficient evaluations of
, which enjoys full calculus induced by the basic one. Efficient evaluations of  for infimum and supremum marginal functions would lead us to refined optimality conditions for both optimistic and pessimistic models in bilevel optimization.
for infimum and supremum marginal functions would lead us to refined optimality conditions for both optimistic and pessimistic models in bilevel optimization.The partial calmness property used in both Theorems 7.8.3 and 7.9.3 seems to be rather restrictive when the lower-level problem is nonlinear with respect to the decision variable. It is a challenging research topic to relax this assumption and to investigate more the uniform weak sharp minimum property and its modifications that yield partial calmness.
One of the possible ways to avoid partial calmness in bilevel programming is as follows. Having the solution map
 to the lower-level problem, consider the constrained upper-level problem given by
to the lower-level problem, consider the constrained upper-level problem given by

 is the cost function on the upper level with the upper-level constraint set
is the cost function on the upper level with the upper-level constraint set  , and where the minimization of
, and where the minimization of  is understood with respect to the standard order on
is understood with respect to the standard order on  . Then (7.10.1) is a problem of set-valued optimization for which various necessary optimality conditions of the coderivative and subdifferential types can be found in [30] and the references therein. Evaluating the coderivatives and subdifferentials of the composition ψ(x, S(x)) in terms of the given lower-level and upper-level data of bilevel programs would lead us to necessary optimality conditions in both optimistic and pessimistic models. There are many open questions arising in efficient realizations of this approach for particular classes of problems in bilevel optimization even with smooth initial data. We refer the reader to the paper by Zemkoho [47] for some recent results and implementations in this direction.
. Then (7.10.1) is a problem of set-valued optimization for which various necessary optimality conditions of the coderivative and subdifferential types can be found in [30] and the references therein. Evaluating the coderivatives and subdifferentials of the composition ψ(x, S(x)) in terms of the given lower-level and upper-level data of bilevel programs would lead us to necessary optimality conditions in both optimistic and pessimistic models. There are many open questions arising in efficient realizations of this approach for particular classes of problems in bilevel optimization even with smooth initial data. We refer the reader to the paper by Zemkoho [47] for some recent results and implementations in this direction.Note that a somewhat related approach to bilevel optimization was developed in [1], where a lower-level problem was replaced by the corresponding KKT system described by a certain generalized equation of the Robinson type [39]. Applying to the latter necessary optimality conditions for upper-level problems with such constraints allowed us to establish verifiable results for the original nonsmooth problem of bilevel programming.
Henrion and Surowiec suggested in [19] a novel approach to derive necessary optimality conditions for optimistic bilevel programs with
 -smooth data and convex lower-level problems. Their approach used a reduction to mathematical programs with equilibrium constraints (MPECs) and allowed them to significantly relax the partial calmness assumption. Furthermore, in this way they obtained new necessary optimality conditions for the bilevel programs under consideration, which are described via the Hessian matrices of the program data.
-smooth data and convex lower-level problems. Their approach used a reduction to mathematical programs with equilibrium constraints (MPECs) and allowed them to significantly relax the partial calmness assumption. Furthermore, in this way they obtained new necessary optimality conditions for the bilevel programs under consideration, which are described via the Hessian matrices of the program data.A challenging direction of the future research is to develop the approach and results from [19] to nonconvex bilevel programs with nonsmooth data. It would be natural to replace in this way the classical Hessian in necessary optimality conditions by the generalized one (known as the second-order subdifferential) introduced by the author in [27] and then broadly employed in variational analysis and its applications; see, e.g., [30] and the references therein.
As it has been long time realized, problems of bilevel optimization are generally ill-posed, which creates serious computational difficulties for their numerical solving; see, e.g., [5, 6, 47] for more details and discussions. Furthermore, various regularization methods and approximation procedures devised in order to avoid ill-posedness have their serious drawbacks and often end up with approximate solutions, which may be far enough from optimal ones. Thus it seems appealing to deal with ill-posed bilevel programs how they are and to develop numerical algorithms based on the obtained necessary optimality conditions. Some results in this vein are presented in [47] with involving necessary optimality conditions of the type discussed here, while much more work is required to be done in this very important direction with practical applications.
This research was partly supported by the USA National Science Foundation under grants DMS-1512846 and DMS-1808978, by the USA Air Force Office of Scientific Research under grant 15RT04, and by Australian Research Council Discovery Project DP-190100555.
The author is indebted to an anonymous referee and the editors for their very careful reading of the original presentation and making many useful suggestions and remarks, which resulted in essential improvements of the paper.







