© Springer Nature Switzerland AG 2020
S. Dempe, A. Zemkoho (eds.)Bilevel OptimizationSpringer Optimization and Its Applications161https://doi.org/10.1007/978-3-030-52119-6_9

9. Algorithms for Simple Bilevel Programming

Joydeep Dutta1   and Tanushree Pandit1  
(1)
Indian Institute of Technology Kanpur, Kanpur, India
 
 
Joydeep Dutta (Corresponding author)
Email: jdutta@iitk.ac.in
 
Tanushree Pandit
Email: tpandit@iitk.ac.in

Abstract

In this article we focus on algorithms for solving simple bilevel programming problems. Simple bilevel problems consist of minimizing a convex function over the solution set of another convex optimization problem. Though the problem is convex the bilevel structure prevents the direct application of the standard methods of convex optimization. Hence several algorithms have been developed in the literature to tackle this problem. In this article we discuss several such algorithms including recent ones.

Keywords
Bilevel programming problemsConvex optimizationProjected gradient methodGradient Lipschitz conditionProximal point methodConvex functionsStrongly convex functions

9.1 Introduction

In this article we focus on the following convex optimization problem (SBP)
../images/480569_1_En_9_Chapter/480569_1_En_9_Equa_HTML.png
Here $$ f,g : \mathbb {R}^n \rightarrow \mathbb {R} $$ are convex functions and C a closed convex set in $$ \mathbb {R}^n $$ . However we could consider $$ f, g : U \rightarrow \mathbb {R} $$ , where U is an open convex set containing C. Further we can also assume that $$ f: \mathbb {R}^n \rightarrow \bar {\mathbb {R}} $$ and $$ g: \mathbb {R}^n \rightarrow \bar {\mathbb {R}} $$ , where $$ \bar {\mathbb {R}} = \mathbb {R} \cup \{-\infty , +\infty \}$$ are proper, lower semi-continuous, convex functions. The problem stated above is called (SBP) to denote the phrase Simple Bilevel Program. The fact that (SBP) has a bilevel structure is evident, while we call it simple since it is represented by only one decision variable in contrast to the two-variable representation in standard bilevel problem. For a detailed discussion on bilevel programming see Dempe [3]. Those readers with an experience in optimization may immediately make the following observation. In general a convex optimization problem may have more than one solution and hence uncountably infinite number of solutions. The decision maker usually would prefer only one among these many solutions. A best way to pick a single solution is to devise a strongly convex objective which is minimized over the solution set of the convex optimization. That gives rise to a simple bilevel problem. The above discussion is explained through the following example.
Example
Consider the following linear programming problem (LP)
$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \min \langle c,x \rangle \\ &\displaystyle &\displaystyle \mbox{subject to } Ax= b, \\ &\displaystyle &\displaystyle x\geq 0. \end{array} \end{aligned} $$
In many situations one needs to find a minimum norm solution of the problem (LP). Thus we may formulate the following simple bilevel problem
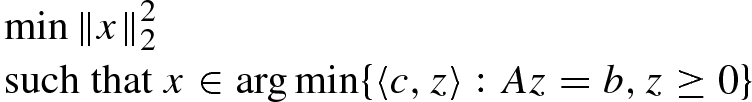
../images/480569_1_En_9_Chapter/480569_1_En_9_Equb_HTML.png
On the other hand if we are seeking a sparse solution then we can formulate the problem as
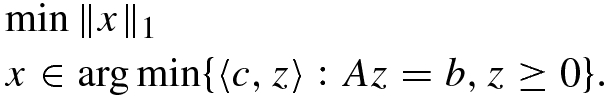
../images/480569_1_En_9_Chapter/480569_1_En_9_Equc_HTML.png
Solodov [22] shows that any standard convex optimization problem can be expressed as a simple bilevel optimization problem. Consider the convex optimization problem (CP)
$$\displaystyle \begin{aligned}&\min f(x) \\& \mbox{subject to } Ax= b,\end{aligned}$$
where $$ f: \mathbb {R}^n \rightarrow \mathbb {R} $$ is convex, A is an m × n matrix, $$ b \in \mathbb {R}^m $$ and each $$ h_i: \mathbb {R}^n \rightarrow \mathbb {R} ,\ i=1,2,\cdots , k $$ is convex. Consider the following simple bilevel problem
../images/480569_1_En_9_Chapter/480569_1_En_9_Eque_HTML.png
where $$ g(x) = \| Ax-b \|{ }^2 + \| \max \{ h(x), 0 \} \|{ }^2 ,\ h(x) = (h_1(x), \cdots , h_k(x))$$ and the maximum is taken component-wise i.e.
$$\displaystyle \begin{aligned} \begin{array}{rcl} \max\{ h(x), 0 \} = (\max\{ h_1(x), 0\}, \cdots, \max\{ h_k(x), 0\} ) \end{array} \end{aligned} $$
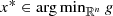Let x ∗ be a feasible point of (CP). Then g(x ∗) = 0 and ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq11_HTML.gif, since g(x) ≥ 0 for all $$ x\in \mathbb {R}^n $$ . This shows that if F is the feasible set of (CP), then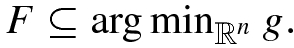
../images/480569_1_En_9_Chapter/480569_1_En_9_Equf_HTML.png
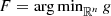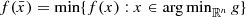Further if g(x ∗) = 0, then x ∗∈ F; showing that ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq13_HTML.gif. This implies that if $$ \bar {x} $$ is a solution of (CP), then ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq15_HTML.gif.

There is another class of problems where the (SBP) formulation may play role in estimating the distance between a feasible point and the solution set of a convex programming problem. This was discussed in Dempe et al. [7]. However for completeness we will also discuss it here through the following example.

Example
Consider a convex programming problem (CP1)
$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \min f(x) \\ &\displaystyle &\displaystyle x \in C, \end{array} \end{aligned} $$
where $$ C = \{ x \in \mathbb {R}^n : g_i(x) \leq 0; i = 1, \cdots , m \} $$ . For this problem the solution set is given as
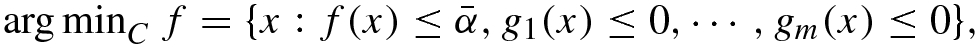
../images/480569_1_En_9_Chapter/480569_1_En_9_Equ4_HTML.png
(9.1.1)
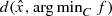where $$ \bar {\alpha } = \inf \limits _{x\in C} f $$ . Given any $$ \hat {x} \in \mathbb {R}^n $$ , suppose we want to estimate ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq19_HTML.gif. In general this may not be so easily done. If we consider 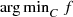../images/480569_1_En_9_Chapter/480569_1_En_9_IEq20_HTML.gif as a system of convex inequalities as shown above in (9.1.1), we can not use the error bound theory in the literature (see for example Lewis and Pang [17] and the references therein) to establish an upper bound to 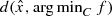../images/480569_1_En_9_Chapter/480569_1_En_9_IEq21_HTML.gif, as the Slater’s condition fails for this system of convex inequalities. One way out of this is to use the simple bilevel programming to estimate 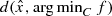../images/480569_1_En_9_Chapter/480569_1_En_9_IEq22_HTML.gif numerically. In fact we can consider the following problem for a given $$ \hat {x} \in \mathbb {R}^n $$ ,
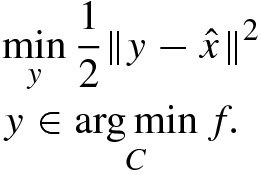
../images/480569_1_En_9_Chapter/480569_1_En_9_Equg_HTML.png
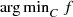Since ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq24_HTML.gif is closed and convex if f and g i’s are finite-valued and $$ \frac {1}{2} \| y- \hat {x} \|{ }^2 $$ is coercive in y and thus a minimizer exists and is unique since $$ \frac {1}{2} \| y- \hat {x} \|{ }^2 $$ is strongly convex in y. Let y ∗ be that unique solution, then
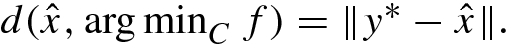
../images/480569_1_En_9_Chapter/480569_1_En_9_Equh_HTML.png
Thus if we want to devise an effective stopping criteria for solving the problem (CP1), one can estimate the distance from the solution set by using the approach of simple bilevel programming. The key idea in developing the algorithms for the simple bilevel programming problem rests on the idea that we shall be able to solve the problem without separately solving the lower level problem.

Note that if in (CP1), f is strongly convex, then an upper bound to 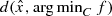../images/480569_1_En_9_Chapter/480569_1_En_9_IEq27_HTML.gif can be computed using the techniques of gap function. See for example Fukushima [24]. 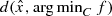If f is convex but not strongly convex then the gap function approach does not seem to work and it appears that at least at present the simple bilevel programming approach is a nice way to estimate ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq28_HTML.gif.

However one may argue that if we consider a linear programming problem, then we can simply use the celebrated Hoffman error bound to devise an upper bound to the solution set. Consider the following linear programming problem
$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \min c^T x,\\ &\displaystyle &\displaystyle \mbox{subject to } \langle a_j, x \rangle \geq b_j, \quad j = 1, \cdots, m\\ &\displaystyle &\displaystyle x_i \geq 0,\quad i = 1,\cdots, n; \end{array} \end{aligned} $$
where $$ c \in \mathbb {R}^n ,\ a_j \in \mathbb {R}^n ,\ b_j \in \mathbb {R} ,\ x_i $$ is the i-th component of the vector $$ x\in \mathbb {R}^n $$ .
Note that we have the solution set given as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{sol}(LP) = \{ x \in \mathbb{R}^n : c^T x \leq \hat{\alpha}, \langle a_j, x \rangle - b_j \geq 0, j=1, \cdots,m ; x_i \geq 0, i=1, \cdots ,n \}, \end{array} \end{aligned} $$
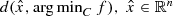where $$ \hat {\alpha } = \inf \limits _{x \in F} c^T x $$ and F is the feasible set of (LP). Though we can use the Hoffmann error bound to get an upper bound to ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq32_HTML.gif; that upper bound will depend on $$ \hat {\alpha } $$ which is never known before hand. 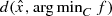Thus even for the case of (LP) we want to argue that the approach through the simple bilevel formulation is better to estimate ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq34_HTML.gif. 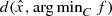Before we end our discussion on this issue we would like to mention that even by using the simple bilevel formulation we are indeed providing an upper bound to ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq35_HTML.gif. Note that while computing the minimizer in the simple bilevel programming formulation, we usually choose an iterate say y k ∈ C as an approximate solution to the bilevel formulation. Hence
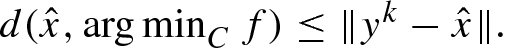
../images/480569_1_En_9_Chapter/480569_1_En_9_Equi_HTML.png

We hope we have been able to convince the reader about the usefulness of the simple bilevel problem. Let us now list down the topics that we shall discuss in rest of the article.

  • Section 9.2: Optimality and links with MPCC

  • Section 9.3: Algorithms for (SBP) with smooth data

  • Section 9.4: Algorithms for (SBP) with non-smooth data.

Let us remind the reader in the beginning that we will discuss the algorithms for (SBP) from the point of view of convergence analysis. We shall not study any complexity related issues or present any numerical experimentation.

9.2 Optimality and Links with MPCC

Optimality conditions lie at the heart of any analysis of optimization problems. In standard bilevel programming, where there are two decision vectors i.e. the leader’s and the follower’s decision vectors, it has been a challenging task to write optimality conditions, since standard constraint qualifications like Mangasarian-Fromovitz constraint qualification (MFCQ) fails at each feasible point of the usual bilevel programming problem. See for example Dempe [3], Dempe et al. [5] and Dutta [10]. The question that arises here is whether the simple bilevel programming problem (SBP) also faces similar hurdles. Let us now look into this issue. When we are concerned with optimality conditions, one of the key step is to reformulate it as an equivalent single-level problem. Assume that the lower-level problem in (SBP) has a finite lower bound. Let us set $$ \alpha = \inf \limits _{x \in C} g(x) $$ . Then (SBP) can be equivalently reformulated as
$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \min f(x)\\ &\displaystyle &\displaystyle \mbox{subject to } g(x) \leq \alpha,\\ &\displaystyle &\displaystyle x \in C. \end{array} \end{aligned} $$
Those who are well-versed with the standard bilevel programming problem would immediately realize that above reformulation is the analogue of the value-function reformulation in the standard case. It is simple to see that the Slater’s condition fails here. If $$ \hat {x} \in C $$ such that $$ g(\hat {x}) < \alpha $$ , then it contradicts the fact that $$ \alpha = \inf \limits _{x \in C } g(x)$$ . Since Slater’s condition fails one may doubt whether the KKT conditions would hold. One might also feel that KKT conditions might hold under more weaker conditions. The KKT condition for the (SBP), is defined to be the KKT condition for the reformulated problem which we will term as (r-SBP). The KKT conditions at any x feasible to (r-SBP) postulates the existence of λ ≥ 0, such that
  1. 1.

    0 ∈ ∂f(x) + λ∂g(x) + N C(x)

     
  2. 2.

    λ(g(x) − α) = 0

     
If x ∗ is the solution of (SBP), then g(x ∗) = α and hence (2) automatically holds. Thus if x ∗ solves (SBP), we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} 0 \in \partial f (x^*) + \lambda \partial g(x) + N_C (x), \end{array} \end{aligned} $$
(9.2.1)
as the required KKT condition. This has to be both necessary and sufficient. Proving sufficiency is not very difficult while proving necessity needs quite involved qualification conditions. See for example Dempe et al. [6], Dhara and Dutta [9] and Dempe et al.[7].
Since (SBP) is a convex programming problem we expect it to have a necessary and sufficient optimality condition which ever way we approach it. However it was shown in Dempe et al. [6], that this is not the case. Consider g to be differentiable convex. In such a case one can equivalently write (SBP) as follows
$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \min f(x)\\ &\displaystyle &\displaystyle \mbox{subject to } 0 \in \nabla g(x) + N_C(x). \end{array} \end{aligned} $$
It has been shown in [6] that necessary optimality condition obtained is not sufficient.
Let us now focus our attention to the case where the lower level problem is a linear programming problem, i.e. consider the (SBP) given as
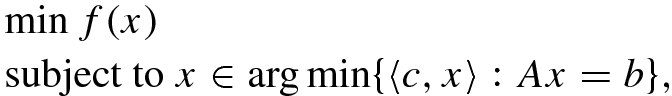
../images/480569_1_En_9_Chapter/480569_1_En_9_Equj_HTML.png
where as before $$ c \in \mathbb {R}^n ,\ A $$ is a m × n matrix and $$ b \in \mathbb {R}^m $$ . For simplicity let us assume that f is differentiable. Assume that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \alpha = \inf \{ \langle c,x \rangle: Ax = b \}. \end{array} \end{aligned} $$
Then we can write down the associated (r-SBP) as
$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \min f(x)\\ &\displaystyle &\displaystyle \mbox{subject to } \langle c,x \rangle \leq \alpha,\\ &\displaystyle &\displaystyle Ax =b. \end{array} \end{aligned} $$
Since (r-SBP) has linear constraints it is well-known that there is no requirement of a constraint qualification for KKT condition to hold. They hold automatically (see Guler [12]).
Let x ∗ be a solution of (SBP) with the lower level problem as a linear problem as given above. Then there exists λ ≥ 0 and $$ \mu \in \mathbb {R}^m $$ such that
$$\displaystyle \begin{aligned} \begin{array}{rcl} 0= \nabla f(x^*) + \lambda c - A^T \mu \end{array} \end{aligned} $$
i.e.
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \nabla f(x^*) =A^T \mu - \lambda c. \end{array} \end{aligned} $$
(9.2.2)
Let x ∗ be a feasible point of (SBP) and assume that there exists $$\mu \in \mathbb {R}^m $$ and λ ≥ 0, such that (9.2.2) holds. Then is x ∗ a solution of (SBP)? To answer this question it is important to note that x ∗ is also feasible for (r-SBP) as 〈c, x〉 = α. Now we have the following simple steps which we provide for completeness. For any feasible x for (SBP) we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} f(x) - f(x^*) \geq \langle \nabla f(x^*) , x- x^* \rangle ,\\ \langle c,x \rangle -\langle c,x^* \rangle = \langle c,x- x^* \rangle. \end{array} \end{aligned} $$
These two together imply that
$$\displaystyle \begin{aligned} \begin{array}{rcl} f(x) - f(x^*) + \lambda \langle c,x \rangle - \lambda \langle c,x^* \rangle \geq \langle \nabla f(x^*) + \lambda c , x- x^* \rangle. \end{array} \end{aligned} $$
Now as 〈c, x〉 = 〈c, x ∗〉 = α, using (9.2.2) we have,
$$\displaystyle \begin{aligned} \begin{array}{rcl} f(x) - f(x^*) \geq \langle A^T \mu,x- x^* \rangle. \end{array} \end{aligned} $$
This implies that
$$\displaystyle \begin{aligned} \begin{array}{rcl} f(x) - f(x^*) \geq \langle \mu, Ax- Ax^* \rangle. \end{array} \end{aligned} $$
Again as Ax = Ax ∗ = b, we get f(x) − f(x ∗) ≥ 0. Therefore
$$\displaystyle \begin{aligned} \begin{array}{rcl} f(x) \geq f(x^*), \end{array} \end{aligned} $$
which implies that x ∗ is a solution of the (SBP) problem.
In particular, let $$ f(x) = \frac {1}{2} \|x\|{ }^2 $$ and $$ \alpha = \inf \{ \langle c, x \rangle : Ax = b \} $$ . Then x ∗ is a solution of the minimum-norm solution problem of the linear programming problem
$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \min \langle c,x \rangle \\ &\displaystyle &\displaystyle \mbox{subject to } Ax= b, \end{array} \end{aligned} $$
if and only if there exists $$ \mu \in \mathbb {R}^n $$ and λ ≥ 0 such that
$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle x^* = A^T \mu - \lambda c \\ &\displaystyle &\displaystyle Ax^* =b \\ &\displaystyle &\displaystyle \langle c,x^* \rangle = \alpha. \end{array} \end{aligned} $$
So the key idea is to first solve the linear programming problem and find α, and then solve the above system of equations to find the minimum norm solution.

9.2.1 Simple Bilevel Programming Problem and MPCC

This subsection focuses in the relation between simple bilevel programming problem (9.2.3) and its corresponding MPCC problem. Here we present some results showing that (SBP) problem exactly follows the standard optimistic bilevel programming problem in this context (see [4] for details). We will show that if the lower level problem of the (SBP) satisfies the Slater condition then it is equivalent to it’s corresponding MPCC problem. Lack of Slater condition leads to counter-examples where (SBP) and related MPCC are not connected in solution sense. The results of this subsection were first presented in the thesis of Pandit [18].

Let us consider the following structure of Simple Bilevel Programming (SBP) problem
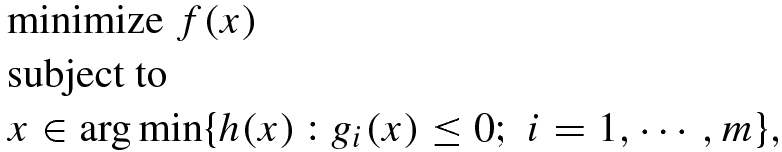
../images/480569_1_En_9_Chapter/480569_1_En_9_Equ21_HTML.png
(9.2.3)
where $$ f,h : \mathbb {R}^n \rightarrow \mathbb {R} $$ are convex functions and for each i ∈{1, ⋯ , m} the functions $$ g_i : \mathbb {R}^n \rightarrow \mathbb {R} $$ are also convex functions. The corresponding MPCC is given by
$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \mbox{minimize } f(x) \\ &\displaystyle &\displaystyle \mbox{subject to} \\ &\displaystyle &\displaystyle \nabla h(x) +\sum_{i=1}^{m}\lambda_i \nabla g_i(x)=0 {} \\ &\displaystyle &\displaystyle g_i(x) \leq 0,~ \lambda_i \geq 0 \\ &\displaystyle &\displaystyle \lambda_i g_i(x)=0 \mbox{ for all } i \in \{ 1, \cdots, m \} . \end{array} \end{aligned} $$
(9.2.4)
(SBP) problem not only follows the optimistic bilevel programming problem, in fact we don’t get any better results for (SBP) problem in spite of the extra convexity properties which lacked in bilevel programming problem. Here we present some results showing that Slater condition is sufficient to establish equivalence between (SBP) and simple MPCC problem.
For any $$x \in \mathbb {R}^n$$ such that g(x) ≤ 0, let us define
$$\displaystyle \begin{aligned} \Lambda (x):= \{\lambda \in \mathbb{R}^m : &\lambda_i \geq 0, \lambda_i g_i(x)=0 \mbox{ for all } i \in \{ 1, \cdots, m \};\\& \nabla h(x) +\sum\limits_{i=1}^{m}\lambda_i \nabla g_i(x)=0 \}. \end{aligned}$$
Then (x, λ) for λ ∈ Λ(x) is a feasible point of the problem (9.2.4).
Theorem 9.2.1

Let $$\bar {x}$$ be a global minimizer of the simple bilevel programming problem (9.2.3) and assume that the lower level problem satisfies the Slater condition. Then for any $$\lambda \in \Lambda (\bar {x})$$ , the point $$(\bar {x}, \lambda )$$ is a global minimizer of the corresponding MPCC Problem (9.2.4). △

Proof
Since $$\bar {x} $$ is the minimizer of the (SBP) problem (9.2.3), thus it is a solution of the lower level problem. Since the Slater condition holds for the lower level problem in (9.2.3), we conclude that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \Lambda (\bar{x}) \neq \emptyset. \end{array} \end{aligned} $$
This immediately shows that for any $$ \lambda \in \Lambda (\bar {x}) $$ , we have $$ ( \bar {x}, \lambda ) $$ to be a feasible point of the (MPCC) problem (9.2.4). Consider any (x, λ′) to be feasible point of the (MPCC) problem (9.2.4), then it is simple to observe by noting the convexity of h and g i’s we conclude that x is feasible for the (SBP) problem (9.2.3). Hence $$ f(x) \geq f(\bar {x}) $$ showing us that $$ ( \bar {x}, \lambda ) $$ , for any $$ \lambda \in \Lambda (\bar {x}) $$ is a solution of the (MPCC). □
Theorem 9.2.2

Assume that the Slater condition hold true for the lower level problem of the (SBP) problem (9.2.3). Let $$(\bar {x}, \bar {\lambda })$$ is a local solution of the MPCC problem (9.2.4). Then $$\bar {x}$$ is a global solution of the SBP problem. △

Proof
Let $$(\bar {x},\bar {\lambda })$$ is a local minimizer of the problem (9.2.4). Then by the definition of a local minimizer, there exists δ > 0, such that
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} f(\bar{x})\leq f(x), \mbox{ for all } ( x, \lambda ), \mbox{ with } \lambda \in \Lambda(x) \mbox{ and } \|(x,\lambda)-(\bar{x}, \bar{\lambda})\| < \delta. \end{array} \end{aligned} $$
(9.2.5)
Since the Slater condition holds for the lower level problem, it is well-known fact that if x and $$ \bar {x} $$ are two different global minimizers of the lower level problem of (9.2.3), then
$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \Lambda(x) = \Lambda( \bar{x}). \end{array} \end{aligned} $$
(9.2.6)
For a proof of (9.2.6) see for example in Dhara and Dutta [9]. Since $$(\bar {x},\bar {\lambda })$$ is feasible for MPCC it is clear that $$ \bar {x} $$ is a solution of the lower level problem of the (SBP) problem (9.2.3). We will now demonstrate that $$ \bar {x} $$ is a local solution of the (SBP) problem and hence it would be a global one as (SBP) is a convex programming problem.
Let x be feasible for the (SBP) problem (9.2.3) such that
$$\displaystyle \begin{aligned} \| x- \bar{x} \| < \delta. \end{aligned}$$
Slater condition guarantees that Λ(x) ≠ ∅. Hence by (9.2.6), $$ \bar {\lambda } \in \Lambda (x)$$ . Now consider the same δ as above. Then
$$\displaystyle \begin{aligned} \| (x, \bar{\lambda}) - (\bar{x},\bar{\lambda}) \| < \delta. \end{aligned}$$
Thus from our discussion above we have $$ f(x) \geq f(\bar {x}) $$ . Hence $$ \bar {x} $$ is a local minimizer of the (SBP) problem and thus a global one. □
Corollary 9.2.3

Let the Slater’s condition holds for the lower level problem of the SBP (9.2.3). Then $$(\bar {x}, \bar {\lambda })$$ is a local solution of the corresponding simple MPCC problem (9.2.4), which implies that $$(\bar {x}, \bar {\lambda })$$ is a global solution of the problem (9.2.4).

△

We omit the simple proof which is an application of Theorem 9.2.2 followed by Theorem 9.2.1. Corollary 9.2.3 tells us that the (MPCC) problem (9.2.4) is an example of a non-convex problem whose local minimizers are global minimizers also if the Slater condition holds for the lower level problem of the (SBP) problem (9.2.3).

In the above results one must have observed the key role played by the Slater condition. However if the Slater condition fails, the solution of one of the problems (9.2.3) or (9.2.4) may not lead to a solution of the other.

Example

(Slater’s condition holds and the solution of SBP and simple MPCC are same).

Let
$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle f(x)= (x-\frac{1}{2})^2\\ &\displaystyle &\displaystyle h(x) = x^2\\ &\displaystyle &\displaystyle g_1(x)= -x \\ &\displaystyle &\displaystyle g_2(x)= x-3 \end{array} \end{aligned} $$
Then Slater’s condition holds as g 1(2) < 0 and g 2(2) < 0.
Here the feasible set for the simple MPCC problem is
$$\displaystyle \begin{aligned} \begin{array}{rcl} \{(x,\lambda_1, \lambda_2): x=0 , \lambda_1 \geq 0, \lambda_2 = 0 \} \end{array} \end{aligned} $$
Hence the global optimal solution for the simple MPCC problem is x = 0 with optimal value $$f(0)=\frac {1}{4}$$ .
The feasible set of the SBP problem is
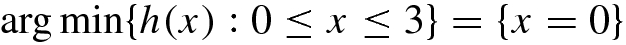
../images/480569_1_En_9_Chapter/480569_1_En_9_Equn_HTML.png
Therefore the global solution of the SBP problem is same as the simple MPCC i.e. x = 0.
Example

SBP has unique solution but corresponding simple MPCC is not feasible (Slater’s condition is not satisfied).

Let
$$\displaystyle \begin{aligned} \begin{array}{rcl} &amp;\displaystyle &amp;\displaystyle f(x_1,x_2)= x_1 +x_2 \\ &amp;\displaystyle &amp;\displaystyle h(x_1,x_2)= x_1 \\ &amp;\displaystyle &amp;\displaystyle g_1(x_1,x_2)= x_1^2 -x_2 \\ &amp;\displaystyle &amp;\displaystyle g_2(x_1,x_2)= x_2 \end{array} \end{aligned} $$
Clearly, g 1(x 1, x 2) ≤ 0 and g 2(x 1, x 2) ≤ 0 together imply that x 1 = 0 = x 2. Which implies that Slater’s condition fails for the lower level problem of the SBP.
Now, the feasible set for the SBP problem is
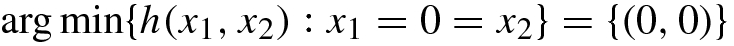
../images/480569_1_En_9_Chapter/480569_1_En_9_Equo_HTML.png
Therefore, (0, 0) is the solution of the SBP problem.
But for x 1 = 0 = x 2, there does not exists λ 1 ≥ 0 and λ 2 ≥ 0 such that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \nabla h(x_1,x_2) + \lambda_1 \nabla g_1(x_1,x_2) + \lambda_2 \nabla g_2(x_1,x_2)=0 \end{array} \end{aligned} $$
Therefore the simple MPCC problem is not feasible even when the SBP has unique solution in case of the failure of Slater’s condition.

9.3 Algorithms for Smooth Data

To the best of our knowledge the first algorithmic analysis was carried out by Solodov [22] in 2007, though the more simpler problem of finding the least norm solution was tackled by Beck and Sabach [1] in 2014 and then a strongly convex upper level objective was considered by Sabach and Shtern [20] in 2017. While writing an exposition it is always a difficult task as to how to present the subject. Shall one concentrate on the simpler problem first or shall one present in a more historical way. After some deliberations we choose to maintain the chronological order of the development so the significance of the simplifications would be more clear.

Let us recall the problem (SBP) given as
../images/480569_1_En_9_Chapter/480569_1_En_9_Equp_HTML.png
where $$ f: \mathbb {R}^n \rightarrow \mathbb {R} $$ and $$ g: \mathbb {R}^n \rightarrow \mathbb {R} $$ are smooth convex functions and C is a closed, convex set.
We shall present here the key ideas from Solodov [22] in a manner that highlights the difficulties in developing a convergent scheme for (SBP). The key idea in Solodov’s approach is that of penalization. He constructs the function
$$\displaystyle \begin{aligned} \begin{array}{rcl} \varphi_{\varepsilon}(x) = g(x) + \varepsilon f(x),\quad \varepsilon &gt;0; \end{array} \end{aligned} $$
where ε varies along iteration. Hence we have sequence of positive numbers {ε k}, and
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \lim\limits_{k \rightarrow \infty} \varepsilon_k =0 \quad \mbox{and} \quad \sum_{k = 0}^{\infty} \varepsilon_k = + \infty. \end{array} \end{aligned} $$
(9.3.1)
In effect we are going minimize at each step functions of the form
$$\displaystyle \begin{aligned} \begin{array}{rcl} \varphi_{\varepsilon_k} (x) = g(x) + \varepsilon_k f(x), \quad \varepsilon_k &gt; 0 \end{array} \end{aligned} $$
with ε k satisfying (9.3.1) over the set C.
Solodov then applies the projected gradient method and develops a scheme for (SBP). Let us try to understand why such a penalization scheme is interesting for (SBP). We believe the key lies in the reformulated version of (SBP), i.e. (r-SBP), which we write as
$$\displaystyle \begin{aligned} \begin{array}{rcl} &amp;\displaystyle &amp;\displaystyle \min f(x)\\ &amp;\displaystyle &amp;\displaystyle g(x) \leq \alpha\\ &amp;\displaystyle &amp;\displaystyle x\in C. \end{array} \end{aligned} $$
The usual penalization schemes may not work as α is involved but a direct penalization can be done and one can write down the following penalty problem
$$\displaystyle \begin{aligned} \begin{array}{rcl} \min\limits_{x\in C} f(x) + \frac{1}{\varepsilon} (g(x) - \alpha). \end{array} \end{aligned} $$
Now for each value of $$ \varepsilon ,\ \displaystyle \frac {\alpha }{\varepsilon }$$ is a fixed quantity, thus it is enough to minimize $$ f(x) + \displaystyle \frac {1}{\varepsilon } g(x) $$ . The minimizer of this function will also minimize εf(x) + g(x) and thus we can use this format to design algorithms for (SBP). Let us understand that this approach will remain very fundamental to design algorithms for (SBP).
Solodov’s Scheme (Algo-SBP-1 [22])

  • Step 0: Choose parameters $$ \bar {\beta }&gt;0, \vartheta \in (0,1) $$ and η ∈ (0, 1). Choose an initial point x 0 ∈ C, ε > 0, k := 0.

  • Step 1: Given x k, let us compute x k+1 = z k(β k); where
    $$\displaystyle \begin{aligned} \begin{array}{rcl}{} z^k(\beta) = \mbox{Proj}_C(x^k - \beta \nabla \varphi_{\varepsilon_k}(x^k)) \end{array} \end{aligned} $$
    (9.3.2)
    and $$ \beta _k = \eta ^{m_k} \bar {\beta }$$ , where m k is the smallest non-negative integer for which the following Armijo type criteria holds, i.e.
    $$\displaystyle \begin{aligned} \begin{array}{rcl}{} \varphi_{\varepsilon_k}(z^k(\eta^{m_k} \bar{\beta})) \leq \varphi_{\varepsilon_k}(x^k) + \vartheta \langle \nabla \varphi_{\varepsilon_k}(x^k), z^k(\eta^{m_k} \bar{\beta}) - x^k \rangle. \end{array} \end{aligned} $$
    (9.3.3)

  • Step 2: Set 0 < ε k+1 < ε k; set k := k + 1 and repeat.

The important issue is how to stop the algorithm. Of course if we have for some k,
$$\displaystyle \begin{aligned} \begin{array}{rcl} x^k = x^{k+1} = z^k(\beta_k) = \mbox{Proj}_C(x^k - \beta_k \nabla \varphi_{\varepsilon_k} (x^k)), \end{array} \end{aligned} $$
where $$ \beta _k = \eta ^{m_k} \bar {\beta } $$ , where m k is as given in the scheme then it is clear that x k is the solution. However this is not the usual scenario and hence one needs to have a stopping criteria for the above algorithm while implementing the algorithm in practice. A good criteria may be to set a threshold ε 0 > 0 and stop when for a given k,
$$\displaystyle \begin{aligned} \begin{array}{rcl} \| x^{k+1} - x^k \| &lt; \varepsilon_0. \end{array} \end{aligned} $$
One needs to be cautioned that this algorithm is useful for those cases of (SBP) where the projection on the set C can be computed easily.

Let us now discuss the convergence analysis. One of the key assumptions is that the gradients of f and g are Lipschitz continuous over bounded sets. However for simplicity in our exposition, we shall consider ∇f and ∇g are Lipschitz continuous on $$ \mathbb {R}^n $$ with Lipschitz constant L > 0. So our assumption (A) will be as follows.

Assumption A

∇f and ∇g are Lipschitz continuous on $$ \mathbb {R}^n $$ with Lipschitz constant L > 0.

For examples of functions for which the gradient is Lipschitz continuous over $$ \mathbb {R}^n $$ , see Beck and Sabach [1]).

Further the fact that ∇f and ∇g are Lipschitz with Lipschitz constant L > 0 is equivalent to the fact that
$$\displaystyle \begin{aligned} \begin{array}{rcl} f(y) - f(x) - \langle \nabla f(x), y-x \rangle \leq \frac{L}{2} \| y-x\|{}^2, \\ g(y) - g(x) - \langle \nabla g(x), y-x \rangle \leq \frac{L}{2} \| y-x\|{}^2, \end{array} \end{aligned} $$
for any $$ x, y \in \mathbb {R}^n $$ .

For the convergence analysis Solodov considers the following assumptions which we mark here as Assumption B; which is as follows.

Assumption B

$$ \bar {f} &gt; - \infty $$ , where $$ \bar {f} = \inf \{ f(x): x \in C \}$$ and $$ \bar {g} &gt; -\infty $$ , where $$ \bar {g} = \inf \{ g(x): x \in C \} $$ . Also we assume that C is non-empty.

A key feature to observe is that we will generate the same iterates if instead of $$\varphi _{\varepsilon _k},\ k\in \mathbb {N}$$ , we successively minimize
$$\displaystyle \begin{aligned} \begin{array}{rcl} \tilde{\varphi}_{\varepsilon_k}(x) = (g(x)- \bar{g}) + \varepsilon(f(x)-\bar{f}) \end{array} \end{aligned} $$
over the set C.

Of course we will begin by assuming that the (SBP) is solvable and hence the second assumption in Assumption B automatically holds.

Solodov [22] begins his analysis by proving a key lemma which says that finding the step size using the Armijo type rule indeed terminates, thus showing that algorithm described above is well-defined. The following lemma is presented in Solodov [22].

Lemma 9.3.1
Let C be a closed convex set and the Assumption Aholds. Then there is finite non-negative integer m k, such that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \beta_k = \eta^{m_k} \bar{\beta} \geq \min \{ \bar{\beta}, \frac{2(1-\vartheta)}{(1+\varepsilon_k)L}\} &gt; 0 \end{array} \end{aligned} $$

and hence the step-size selection procedure at the k-th iteration terminates. △

Proof
We shall outline the main ideas of the proof for completeness. Using (9.3.2) from the algorithm we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle x^k -\beta \nabla \varphi_{\varepsilon_k}(x^k) - z^k(\beta), x^k - z^k(\beta) \rangle \leq 0, \end{array} \end{aligned} $$
implying that
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \| z^k(\beta)-x^k \|{}^2 \leq \beta \langle \nabla \varphi_{\varepsilon_k}(x^k), x^k-z^k(\beta) \rangle. \end{array} \end{aligned} $$
(9.3.4)
By Assumption A, $$ \nabla \varphi _{\varepsilon _k} $$ is Lipschitz on $$\mathbb {R}^n $$ with Lipschitz constant (1 + ε k)L. This shows that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \varphi_{\varepsilon_k}(z^k(\beta)) \leq \varphi_{\varepsilon_k}(x^k) + (1- \frac{L(1+ \varepsilon_k)\beta}{2}) \langle \nabla \varphi_{\varepsilon_k}(x^k),z^k(\beta) - x^k \rangle. \end{array} \end{aligned} $$
If $$ 1- \frac {L(1+ \varepsilon _k)\beta }{2} \leq \vartheta $$ , then $$ \beta \geq \frac {2(1-\vartheta )}{(1+\varepsilon _k)L}$$ . Now $$ \beta _k \leq \bar {\beta } $$ by construction. Hence
$$\displaystyle \begin{aligned} \begin{array}{rcl} \beta_k = \eta^{m_k} \bar{\beta} \geq \min \{ \bar{\beta}, \frac{2(1-\vartheta)}{(1+\varepsilon_k)L} \}. \end{array} \end{aligned} $$
□

It is important to have a closer look at the last expression of the proof. If $$ \bar {\beta } &lt; \frac {2(1-\vartheta )}{(1+\varepsilon _k)L} $$ , then $$ \beta _k \geq \bar {\beta } $$ . But as $$ \beta _k \leq \bar {\beta } $$ , in such a case $$ \beta _k = \bar {\beta } $$ . This case may not be very likely in real implementation.

We shall now look into the issue of convergence analysis. We shall present the key convergence result and then outline the key steps of proof and highlighting the key points which are hallmark of the (SBP) problem.

Theorem 9.3.2 ([22])
Let us consider the problem (SBP), where f and g are convex differentiable functions. Let the Assumptions Aand Bhold. Let the solution set of (SBP), denoted as sol(SBP) be closed and bounded. Then for any sequence x kgenerated by the algorithm (Algo-SBP-1), with the sequence {ε k}, ε k ↓ 0, satisfying (9.3.2), we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} d_{\mathit{\mbox{sol(SBP)}}} (x^k) \rightarrow 0 \quad \mathit{\mbox{as }} k \rightarrow \infty. \end{array} \end{aligned} $$

Here d C(x) represents the distance of the set C from the point x. △

Proof (Outline of the Main Ideas)
The key idea of the proof lies in replacing $$ \varphi _{\varepsilon _k} $$ with $$ \widetilde {\varphi _{\varepsilon _k}} $$ , for each k and rewriting (Algo-SBP-1) in terms of $$ \widetilde {\varphi _{\varepsilon _k}} $$ . In such a case the Armijo type criteria shows that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \vartheta \langle \nabla \tilde{\varphi}_{\varepsilon_k}(x^k), x^k - x^{k+1} \rangle \leq \tilde{\varphi}_{\varepsilon_k}(x^k)- \tilde{\varphi}_{\varepsilon_k}(x^{k+1}). \end{array} \end{aligned} $$
This shows that
$$\displaystyle \begin{aligned} &amp;\vartheta \langle \nabla \tilde{\varphi}_{\varepsilon_k}(x^k), x^k - x^{k+1} \rangle\\ \leq &amp;\ \varepsilon_k (f(x^k)-\bar{f}) + (g(x^k)-\bar{g}) -\varepsilon_k (f(x^{k+1})-\bar{f}) - (g(x^{k+1})-\bar{g}),\end{aligned}$$
i.e.
$$\displaystyle \begin{aligned} \begin{array}{rcl}{}\begin{aligned} &amp;\displaystyle \vartheta \langle \nabla \tilde{\varphi}_{\varepsilon_k}(x^k), x^k - x^{k+1} \rangle \\\leq &amp;\displaystyle \ \varepsilon_k (f(x^k)-\bar{f}) -\varepsilon_k (f(x^{k+1})-\bar{f})+ (g(x^k)-\bar{g}) - (g(x^{k+1})-\bar{g}).\qquad \end{aligned} \end{array} \end{aligned} $$
(9.3.5)
Now by the definition of $$ \bar {f},\ \bar {f} \leq f(x^k) $$ for all $$ k \in \mathbb {N}$$ as x k ∈ C. Also note that ε k+1 ≤ ε k. Therefore for any $$ k \in \mathbb {N}$$
$$\displaystyle \begin{aligned} 0 \leq \varepsilon_{k+1} (f(x^{k+1}) - \bar{f}) \leq \varepsilon_{k} (f(x^{k+1}) - \bar{f}) \end{aligned}$$
Then from (9.3.5), we get
$$\displaystyle \begin{aligned} \begin{array}{rcl}\begin{aligned} &amp;\displaystyle \vartheta \langle \nabla \tilde{\varphi}_{\varepsilon_k}(x^k), x^k - x^{k+1} \rangle \\ \leq &amp;\displaystyle \ \varepsilon_k (f(x^k)-\bar{f}) -\varepsilon_{k+1} (f(x^{k+1})-\bar{f})+ (g(x^k)-\bar{g}) - (g(x^{k+1})-\bar{g}).\end{aligned} \end{array} \end{aligned} $$
Since this holds for all $$ k \in \mathbb {N}$$ , by summing over from k = 0 to $$ k = \hat {k} $$ , we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} &amp;\displaystyle &amp;\displaystyle \vartheta \sum_{k= 0}^{\hat{k}} \langle \nabla \tilde{\varphi}_{\varepsilon_k}(x^k), x^k - x^{k+1} \rangle \\\leq&amp;\displaystyle &amp;\displaystyle \varepsilon_0 (f(x^0)-\bar{f}) + (g(x^0)-\bar{g}) - \varepsilon_{k+1} (f(x^{\hat{k}+1})-\bar{f})- (g(x^{\hat{k}+1})-\bar{g})\\ \leq &amp;\displaystyle &amp;\displaystyle \varepsilon_0 (f(x^0)-\bar{f}) + (g(x^0)-\bar{g}). \end{array} \end{aligned} $$
We urge the reader to check the above inequality themselves. Now as $$ \hat {k} \rightarrow \infty $$ , we conclude that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{k= 0}^{\infty} \langle \nabla \tilde{\varphi}_{\varepsilon_k}(x^k), x^k - x^{k+1} \rangle \leq \frac{1}{\vartheta}[\varepsilon_0 (f(x^0)-\bar{f}) + (g(x^0)-\bar{g})] &lt; + \infty. \end{array} \end{aligned} $$
Thus the series $$ \sum \limits _{k= 0}^{\infty } \langle \nabla \tilde {\varphi }_{\varepsilon _k}(x^k), x^k - x^{k+1} \rangle $$ is summable and hence
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \langle \nabla \tilde{\varphi}_{\varepsilon_k}(x^k), x^k - x^{k+1} \rangle \rightarrow 0 \quad \mbox{as } k \rightarrow \infty. \end{array} \end{aligned} $$
(9.3.6)
From the point of view of convergence analysis it is important that the sequence generated by the algorithm is bounded. In that case an effort should be made to show that any limit point of that sequence is in the solution set of the problem under consideration. In fact in the setting of bilevel programming it is slightly tricky to show that {x k} is bounded. Rather it is much easier to show that if {x k} is bounded, then every limit point will be a solution of the lower level problem. This is the approach taken by Solodov [22] and we will outline this approach here. We shall then show that {x k} is bounded and the accumulation points indeed belong to sol(SBP). Our first step would be to show that for any bounded {x k} generated by (Algo-SBP-1) a limit point is always a solution of the lower level problem. Now from the algorithm we know that 0 < ε k+1 < ε k < ε 0. Thus
$$\displaystyle \begin{aligned} \begin{array}{rcl} \beta_k \geq \min \{ \bar{\beta}, \frac{2(1-\vartheta)}{(1+\varepsilon_0)L} \} = \hat{\beta} \mbox{ (say)}. \end{array} \end{aligned} $$
(9.3.7)
Using (9.3.4) and (9.3.6) we conclude that ∥x k − x k+1∥→ 0 and hence
$$\displaystyle \begin{aligned} \begin{array}{rcl} x^k - x^{k+1} \rightarrow 0. \end{array} \end{aligned} $$
Thus by definition, as k → 0
$$\displaystyle \begin{aligned} \begin{array}{rcl} x^k - \mbox{proj}_C (x^k - \beta_k \nabla \tilde{\varphi}_{\varepsilon_k}(x^k)) \rightarrow 0 . \end{array} \end{aligned} $$
Hence let $$ \tilde {x} $$ be an accumulation point or limit point of {x k} then as k → 0
$$\displaystyle \begin{aligned} \begin{array}{rcl} \tilde{x} - \mbox{proj}_C (\tilde{x} - \tilde{\beta} \nabla \tilde{\varphi}_{\varepsilon_k}(\tilde{x})) = 0 , \end{array} \end{aligned} $$
where $$ \beta _k \rightarrow \tilde {\beta } &gt;0 $$ (Noting that it is simple to show that β k is bounded). Hence $$ \tilde {x} = \mbox{proj}_C (\tilde {x} - \tilde {\beta } \nabla \tilde {\varphi }_{\varepsilon _k}(\tilde {x})) $$ showing that $$ \tilde {x} $$ is the solution of the lower level problem. But before we establish that $$\tilde {x}$$ also lies in sol(SBP), we shall show that {x k} is bounded. Using the fact that the sol(SBP) is non empty, closed and bounded; Solodov starts the analysis of this part by considering an $$\bar {x} \in \mbox{sol(SBP)}$$ . Now convexity of $$ \varphi _{\varepsilon _k}$$ will show us that
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \langle \nabla \tilde{\varphi}_{\varepsilon_k}, \bar{x}- x^k \rangle \leq \varepsilon_k (f(\bar{x})- f(x^k)). \end{array} \end{aligned} $$
(9.3.8)
Solodov then employs the following identity
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \| x^{k+1} - \bar{x} \|{}^2 - \| x^{k+1} - x^k \|{}^2 = \|x^k - \bar{x} \|{}^2 + 2 \langle x^{k+1} - x^k , x^{k+1} - \bar{x} \rangle.\qquad \end{array} \end{aligned} $$
(9.3.9)
Note that,
$$\displaystyle \begin{aligned} &amp;\langle x^{k+1}- x^k , x^{k+1} - \bar{x} \rangle\\ =&amp;\ \langle x^{k+1}- x^k + \beta_k \nabla \tilde{\varphi}_{\varepsilon_k}(x^k)-\beta_k \nabla \tilde{\varphi}_{\varepsilon_k}(x^k), x^{k+1} - \bar{x} \rangle\\ =&amp;\ \langle x^{k+1}- x^k + \beta_k \nabla \tilde{\varphi}_{\varepsilon_k}(x^k), x^{k+1} - \bar{x} \rangle - \beta_k \langle \nabla \tilde{\varphi}_{\varepsilon_k}(x^k),x^{k+1} - \bar{x} \rangle. \end{aligned}$$
Since by the algorithm
$$\displaystyle \begin{aligned} \begin{array}{rcl} x^{k+1} = \mbox{proj}_C (x^k - \beta_k \nabla\tilde{\varphi}_{\varepsilon_k}(x^k)), \end{array} \end{aligned} $$
(9.3.10)
by the well known property of projection (see e.g. Hirriart Urruty and Lemarechal [14]) we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle x^k - \beta_k \nabla\tilde{\varphi}_{\varepsilon_k}(x^k) - x^{k+1}, \bar{x} - x^{k+1} \rangle \leq 0\\ \mathit{i.e.}\ \langle x^k - \beta_k \nabla\tilde{\varphi}_{\varepsilon_k}(x^k) - x^{k+1}, x^{k+1}-\bar{x} \rangle \geq 0 \end{array} \end{aligned} $$
Hence from this we can deduce by noting that $$ \beta _k \leq \bar {\beta } $$ and (9.3.8),
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle x^{k+1} - x^k, x^{k+1} - \bar{x} \rangle \leq \bar{\beta} \langle \nabla\tilde{\varphi}_{\varepsilon_k}(x^k)), x^k - x^{k+1} \rangle + \beta_k \varepsilon_k (f(\bar{x}) - \bar{f}). \end{array} \end{aligned} $$
Now from (9.3.9) and using the above relations, we have
$$\displaystyle \begin{aligned} \begin{array}{rcl}\begin{aligned}{} &amp;\displaystyle \| x^{k+1} - \bar{x} \|{}^2 \\ \leq&amp;\displaystyle \ \| x^{k} - \bar{x} \|{}^2 + 2\bar{\beta} \langle \nabla\tilde{\varphi}_{\varepsilon_k}(x^k)), x^k - x^{k+1} \rangle + 2 \beta_k \varepsilon_k (f(\bar{x}) - f(x^k)).\end{aligned}\quad \end{array} \end{aligned} $$
(9.3.11)
We need to focus on the quantity $$ (f(\bar {x}) - f(x^k)) $$ , an information about the second term on the right hand side is given by (9.3.6). Now one needs to look into two separate cases formally.
Case I :

There exists k 0, such that one has $$ f(\bar {x}) \leq f(x^k) $$ , for all k ≥ k 0.

Case II :

For any $$ k \in \mathbb {N} $$ , there exists $$ k_1 \in \mathbb {N} $$ and k 1 ≥ k such that $$ f(\bar {x}) &gt; f(x^{k_1}) $$ .

We first deal with Case I. It is shown in Solodov [22] that using case I, (9.3.11) gives
$$\displaystyle \begin{aligned} \begin{array}{rcl} \| x^{k+1} - \bar{x} \|{}^2 \leq \| x^{k} - \bar{x} \|{}^2 + 2\bar{\beta} \langle \nabla\tilde{\varphi}_{\varepsilon_k}(x^k)), x^k - x^{k+1} \rangle \end{array} \end{aligned} $$
(9.3.12)
This shows that $$ \{ \|x^k - \bar {x} \|{ }^2 \} $$ converges since if {a k} and {b k} are sequences of non-negative real numbers such that a k+1 ≤ a k + b k and $$ \sum \limits _{k=1}^{\infty } b_k &lt; + \infty $$ , then {a k} converges. Hence {x k} is bounded. Solodov [22] then proves that
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \liminf\limits_{k \rightarrow \infty} f(x^k) = f(\bar{x}) \end{array} \end{aligned} $$
(9.3.13)
Hence we can find a convergent subsequence of $$ \{ x^{k_j} \} $$ of {x k} such that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \liminf\limits_{j \rightarrow \infty} f(x^{k_j}) = f(\bar{x}). \end{array} \end{aligned} $$
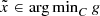Let $$ x^{k_j} \rightarrow \tilde {x} $$ as j →∞. Hence $$ f(\tilde {x}) = f(\bar {x}) $$ . We have seen before that ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq125_HTML.gif and thus $$ \tilde {x} \in \mbox{sol(SBP)} $$ .
Solodov [22] then shows that if we set $$ \tilde {x} = \bar {x} $$ , then we can demonstrate that $$ x^k \rightarrow \tilde {x} $$ as k →∞. Now looking at the proof above we can show that $$ \{ \| x^k - \tilde {x} \|{ }^2 \} $$ converges. Since $$ x^{k_j} \rightarrow \tilde {x} $$ ; there is a subsequence of $$ \{ \| x^k - \tilde {x} \|{ }^2 \} $$ that converges to 0. Hence the sequence $$ \{ \| x^k - \tilde {x} \|{ }^2 \} $$ converges to 0, which implies that $$ x^k \rightarrow \tilde {x} \in \mbox{sol(SBP)}$$ . This argument is a very crucial one as one observes. For details see Solodov [22]. Handling the second case is more complicated since we have to deal essentially with subsequences. One of the main tricks of this approach is to define the following quantity i k for each $$ k \in \mathbb {N} $$ as
$$\displaystyle \begin{aligned} \begin{array}{rcl} i_k = \max \{i \leq k : f(\bar{x}) &gt; f(x^i)\} \end{array} \end{aligned} $$
An important thing to observe is that for a given k one may have $$ \{ i \leq k : f(\bar {x}) &gt; f(x^i) \} = \emptyset $$ and in that case i k can not be defined. Thus a better way to write is that let $$ \hat {k} \in \mathbb {N} $$ be first integer for which
$$\displaystyle \begin{aligned} \begin{array}{rcl} \{ i \leq \hat{k} : f(\bar{x}) &gt; f(x^i) \} \end{array} \end{aligned} $$
is non-empty. Then for all $$ k \geq \hat {k} $$ and $$ k \in \mathbb {N} $$ we can define
$$\displaystyle \begin{aligned} \begin{array}{rcl} i_k = \max \{ i \leq k : f(\bar{x}) &gt; f(x^i) \}. \end{array} \end{aligned} $$
Thus we shall only consider now $$ k \geq \hat {k} $$ . Also from the description of Case II, we can conclude that i k →∞ as k →∞.
The key step now is to show that $$ \{ x^{i_k} \}_{k= \hat {k}}^{\infty } $$ is bounded. Let us observe that
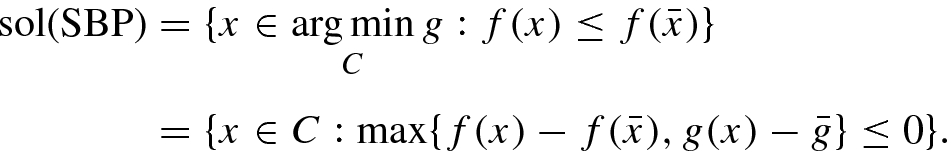
../images/480569_1_En_9_Chapter/480569_1_En_9_Equt_HTML.png
The function $$ \psi (x) = \max \{ f(x) - f(\bar {x}), g(x) - \bar {g} \} $$ is a convex function. This shows that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{sol(SBP)} = \{ x \in C : \psi(x) \leq 0 \}. \end{array} \end{aligned} $$
Now sol(SBP) is assumed to be non empty and bounded. The level set {x ∈ C : ψ(x) ≤ 0} = L ψ(0) of the convex function ψ is non empty and bounded. Further it is well known that in such a case for any $$ q \in \mathbb {R} $$ ,
$$\displaystyle \begin{aligned} \begin{array}{rcl} L_{\psi}(q) := \{ x\in C : \psi(x) \leq q \} \end{array} \end{aligned} $$
is also bounded. Solodov [22] then shows that
$$\displaystyle \begin{aligned} \begin{array}{rcl} 0 \leq \tilde{\varphi}_{\varepsilon_{k+1}}(x^{k+1}) \leq \tilde{\varphi}_{\varepsilon_{k}}(x^{k+1}) \leq \tilde{\varphi}_{\varepsilon_{k}}(x^{k}). \end{array} \end{aligned} $$
This is a key step since it shows that the sequence $$ \{ \tilde {\varphi }_{\varepsilon _{k}}(x^{k})\} $$ is non-increasing and bounded below which establishes the fact that $$ \{ \tilde {\varphi }_{\varepsilon _{k}}(x^{k})\} $$ is a convergent sequence and hence bounded. This shows that the sequence $$ \{ g(x^k) - \bar {g} \} $$ is bounded. In the very next step Solodov [22] uses this boundedness of $$ \{ g(x^k) - \bar {g} \} $$ in a profitable way. Let q ≥ 0 be such that $$ g(x^k) - \bar {g} \leq q $$ for all $$ k \in \mathbb {N} $$ .
Now from the definition of i k we have for all $$ k \geq \hat {k} $$
$$\displaystyle \begin{aligned} \begin{array}{rcl} \varepsilon_k (f(x^{i_k})- f(\bar{x})) &lt; 0 \end{array} \end{aligned} $$
and thus
$$\displaystyle \begin{aligned} \begin{array}{rcl} \varepsilon_k (f(x^{i_k})- f(\bar{x})) + (g(x^{i_k})- g(\bar{x})) \leq q \end{array} \end{aligned} $$
implying that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \tilde{\varphi}_{\varepsilon_{i_k}}(x^{i_k}) \leq q \quad \forall \quad k \geq \hat{k}. \end{array} \end{aligned} $$
Hence $$ x^{i_k} \in L_{\tilde {\varphi }_{\varepsilon _{i_k}}} (q) $$ for all $$ k \geq \hat {k} $$ . Thus $$ \{ x^{i_k} \} $$ is bounded. Now for any $$ k \geq \hat {k} $$ , the definition i k tells us that
$$\displaystyle \begin{aligned} \begin{array}{rcl} f(\bar{x}) \leq f(x^i) \end{array} \end{aligned} $$
for i = i k + 1, ⋯ , k; if k > i k. Thus from (9.3.11), we get for i = i k + 1, ⋯ , k
$$\displaystyle \begin{aligned} \begin{array}{rcl} \| x^{i+1} - \bar{x} \|{}^2 \leq \| x^{i} - \bar{x} \|{}^2 + 2 \bar{\beta} \langle \nabla \tilde{\varphi}_{\varepsilon_i}(x^i), x^i - x^{i+1} \rangle. \end{array} \end{aligned} $$
This holds true for all cases where k > i k. Thus we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \| x^k - \bar{x} \|{}^2 \leq \| x^{i_k} - \bar{x} \|{}^2 + 2 \bar{\beta} \sum_{i=i_k +1}^{k-1} \langle \nabla \tilde{\varphi}_{\varepsilon_i}(x^i), x^i - x^{i+1} \rangle, \end{array} \end{aligned} $$
for all k for which i k < k.
Let us now consider the case where i k = k. In that case we will proceed in the following way. For any $$ k \in \mathbb {N} $$ we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} x^{k+1} = \mbox{proj}_C (x^k - \beta_k \nabla \tilde{\varphi}_{\varepsilon_k}(x^k)). \end{array} \end{aligned} $$
From the definition of projection we can conclude that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \| x^{k+1} - x^k \|{}^2 \leq \beta_k \langle \nabla \tilde{\varphi}_{\varepsilon_k}(x^k), x^k - x^{k+1} \rangle. \end{array} \end{aligned} $$
Thus we have for all $$k \in \mathbb {N} $$
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle \nabla \tilde{\varphi}_{\varepsilon_k}(x^k), x^k - x^{k+1} \rangle \geq 0. \end{array} \end{aligned} $$
Observe however that this shows that
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} 0 \leq 2\bar{\beta} \sum_{j = i_k +1}^{k-1} \langle \nabla \tilde{\varphi}_{\varepsilon_j}(x^j), x^j - x^{j+1} \rangle. \end{array} \end{aligned} $$
(9.3.14)
Thus for k with i k = k we have $$ \| x^k - \bar {x} \|{ }^2 = \| x^{i_k} - \bar {x} \|{ }^2 $$ . Hence from (9.3.14)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \| x^k - \bar{x} \|{}^2 \leq \| x^{i_k} - \bar{x} \|{}^2 + 2\bar{\beta} \sum_{j = i_k +1}^{k-1} \langle \nabla \tilde{\varphi}_{\varepsilon_j}(x^j), x^j - x^{j+1} \rangle. \end{array} \end{aligned} $$
So we conclude that for all k we have
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \| x^k - \bar{x} \|{}^2 \leq \| x^{i_k} - \bar{x} \|{}^2 + 2\bar{\beta} \sum_{j = i_k +1}^{\infty} \langle \nabla \tilde{\varphi}_{\varepsilon_j}(x^j), x^j - x^{j+1} \rangle. \end{array} \end{aligned} $$
(9.3.15)
Now i k →∞ as k →∞ we see that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{j = i_k +1}^{\infty} \langle \nabla \tilde{\varphi}_{\varepsilon_j}(x^j), x^j - x^{j+1} \rangle \rightarrow 0 \quad \mbox{as } k \rightarrow \infty. \end{array} \end{aligned} $$
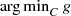Thus using the boundedness of $$ \{ x^{i_k} \} $$ we conclude that {x k} is also bounded. We can immediately conclude that all accumulation points of {x k} lie in ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq158_HTML.gif. Further for any accumulation point x ∗ of $$ \{ x^{i_k} \} $$ we have $$ f(\bar {x}) \geq f(x^*) $$ . But this shows that x ∗∈sol(SBP). In fact all accumulation points of $$ \{ x^{i_k} \} $$ must be in sol(SBP). If x ∗ is an accumulation point of $$ \{ x^{i_k} \} $$ , thus there exists a convergent subsequence $$ \{ x^{i_{k_j}} \} $$ of $$ \{ x^{i_k} \} $$ such that $$ x^{i_{k_j}} \rightarrow x^* $$ as j →∞. Further we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} d(x^{i_{k_j}},\mbox{sol(SBP)}) \leq \| x^{i_{k_j}} - x^* \|. \end{array} \end{aligned} $$
Thus as j →∞ we have
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} d(x^{i_{k_j}},\mbox{sol(SBP)}) \rightarrow 0. \end{array} \end{aligned} $$
(9.3.16)
We can also see that for any convergent subsequence of $$ \{ x^{i_k} \} $$ (9.3.16) holds, this shows that
$$\displaystyle \begin{aligned} \begin{array}{rcl} d( x^{i_{k}},\mbox{sol(SBP)}) \rightarrow 0 \quad \mbox{as } k \rightarrow \infty. \end{array} \end{aligned} $$
Now for each k, Solodov [22] defines
$$\displaystyle \begin{aligned} \begin{array}{rcl} \bar{x}^k = \mbox{proj}_{\mbox{sol(SBP)}} (x^{i_k}). \end{array} \end{aligned} $$
Now using (9.3.15) with $$ \bar {x} = \bar {x}^k $$ we have
$$\displaystyle \begin{aligned} d^2( x^{k},\mbox{sol(SBP)}) \leq &amp; \| x^k - \bar{x}^k \|{}^2 \\ \leq &amp; d^2( x^{i_{k}},\mbox{sol(SBP)}) + 2 \bar{\beta}\sum\limits_{j= i_k +1}^{\infty} \langle \nabla \tilde{\varphi}_{\varepsilon_i} (x^i), x^i - x^{i+1} \rangle. \end{aligned}$$
Now as k →∞ we have d 2(x k, sol(SBP)) → 0, hence d(x k, sol(SBP)) → 0. □
We shall now discuss a work by Beck and Sabach [1], which focuses on what we believe as the most important class of simple bilevel problems. In this case the upper-level objective is always strongly convex. We shall denote such problems as (SBP-1). Thus an (SBP-1) problem is given as
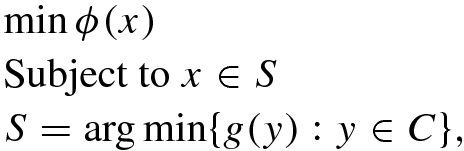
../images/480569_1_En_9_Chapter/480569_1_En_9_Equv_HTML.png
where $$ \phi : \mathbb {R}^n \rightarrow \mathbb {R} $$ is strongly convex with modulus ρ > 0 and differentiable, while $$ g: \mathbb {R}^n \rightarrow \mathbb {R} $$ is a convex and differentiable function with ∇g a Lipschitz function on $$\mathbb {R}^n $$ with Lipschitz rank (or Lipschitz constant) L > 0. When $$ \phi (x) = \frac {1}{2} \|x\|{ }^2 $$ , we are talking about the minimum norm problem. Thus (SBP-1) actually encompasses a large class of important problems.
Beck and Sabach [1] develops the Minimal norm gradient algorithm, which they present in two different versions. For the first version the Lipschitz rank of ∇g is known while for the second version it is assumed that the Lipschitz rank is not known and thus an Armijo type criteria is used. In Solodov [22] in comparison an Armijo type criteria is used even though the Lipschitz rank was known. Also note that in Beck and Sabach [1], the Lipschitz gradient assumption is only on g and not on ϕ. In fact Beck and Sabach [1] mention that a problem like (SBP-1) can be reformulated as follows
$$\displaystyle \begin{aligned} \begin{array}{rcl} &amp;\displaystyle &amp;\displaystyle \min \phi(x)\\ &amp;\displaystyle &amp;\displaystyle \mbox{Subject to } g(x) \leq g^*\\ &amp;\displaystyle &amp;\displaystyle x\in C, \end{array} \end{aligned} $$
where $$ g^* = \inf \limits _{x\in C } g $$ . We are already familiar with this reformulation and further they mention that as the Slater condition fails and g ∗ may not be known, the above problem may not be suitable to develop numerical schemes to solve (SBP-1). They mention that even if one could compute g ∗ exactly, the fact that Slater’s condition fails would lead to numerical problems. As a result they take a completely different path by basing their approach on the idea of cutting planes. However we would like to mention that very recently in the thesis of Pandit [18], the above reformulation has been slightly modified to generate a sequence of problems whose solutions converge to that of (SBP) or (SBP-1), depending on the choice of the problem. The algorithm thus presented in the thesis of Pandit [18] has been a collaborative effort with Dutta and Rao and has also been presented in the preprint [19]. The approach in Pandit et al. [19] has been to develop an algorithm where no additional assumption on the upper level objective is assumed other than the fact that it is convex, where the lower level objective is differentiable but need not have a Lipschitz gradient. The algorithm in Pandit [18] or [19] is very simple and just relies on an Armijo type decrease criteria. Convergence analysis has been carried out and numerical experiments have given encouraging results. Further in Pandit et al. [19], the upper level objective need not be strongly convex.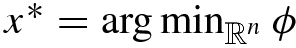
Let us outline the work of Beck and Sabach [1]. Let us begin by mentioning some key tools in [1]. Let
../images/480569_1_En_9_Chapter/480569_1_En_9_Equw_HTML.png
and we call x ∗ the prox-center of ϕ. Without loss of generality we may assume that ϕ(x ∗) = 0. Then strong convexity of ϕ tells us that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \phi(x) \geq \frac{\rho}{2} \| x- x^* \|{}^2 \quad \forall x \in \mathbb{R}^n. \end{array} \end{aligned} $$
A key tool in the study of Beck and Sabach [1] is the Bregman distance. This is a non-Euclidean distance which makes the analysis a bit more involved.
Let $$ h : \mathbb {R}^n \rightarrow \mathbb {R} $$ be a strictly convex function. Then the Bregman distance generated by h is given as
$$\displaystyle \begin{aligned} \begin{array}{rcl} D_{h} (x,y) = h(x) - h(y) - \langle \nabla h(y), x-y \rangle. \end{array} \end{aligned} $$
It is clear that $$ D_h (x,y) \geq 0 ,\ \forall x, y \in \mathbb {R}^n $$ and D h(x, y) = 0 if and only if x = y. Further if h is strongly convex,
$$\displaystyle \begin{aligned} \begin{array}{rcl} D_h(x,y) \geq \frac{\rho}{2} \| x- y \|{}^2. \end{array} \end{aligned} $$
A key inequality associated with a Bregman distance is the well-known three point inequality. If h is strongly convex and $$ x, y,z \in \mathbb {R}^n $$ , then
$$\displaystyle \begin{aligned} \begin{array}{rcl} D_h(x,y) + D_h(y,z) - D_h(x,z) = \langle \nabla h(z) - \nabla h(y) , x-y \rangle. \end{array} \end{aligned} $$
The following two vector-valued mappings play a central role in [1]. First comes the projected gradient mapping or proj-grad mapping. For μ > 0, the proj-grad mapping is given as
$$\displaystyle \begin{aligned} \begin{array}{rcl} P_{M} (x) = \mbox{proj}_C (x - \frac{1}{M} \nabla g(x)), \quad \forall x \in \mathbb{R}^n. \end{array} \end{aligned} $$
The gradient map is defined as
$$\displaystyle \begin{aligned} G_M (x) = M (x- P_M(x)) = M \big(x- \mbox{proj}_C (x- \frac{1}{M} \nabla g(x))\big). \end{aligned}$$
If $$ C = \mathbb {R}^n $$ , then G M(x) = ∇g(x), which is thus the source of its name. Further G M(x ∗) = 0 implies that x ∗ solves the lower level problem in (SBP-1). Further it was shown in [1] that the function
$$\displaystyle \begin{aligned} \begin{array}{rcl} g(M) = \| G_M(x) \|, \quad M&gt;0; \end{array} \end{aligned} $$
is monotonically non-decreasing over (0, ∞). The idea of their algorithm is based on the idea of cutting planes in convex optimization. If $$ x^* \in \mathbb {R}^n $$ is a minimizer of a convex function $$ \phi : \mathbb {R}^n \rightarrow \mathbb {R} $$ , then for any $$ x\in \mathbb {R}^n $$ we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle \nabla \phi(x^*) , x- x^* \rangle \geq 0. \end{array} \end{aligned} $$
By monotonicity, we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle \nabla \phi(x) , x- x^* \rangle \geq 0. \end{array} \end{aligned} $$
Thus if $$\mbox{sol}(\phi , \mathbb {R}^n)$$ denotes the solution set of the problem of minimizing ϕ over $$ \mathbb {R}^n $$ , then
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mbox{sol}(\phi, \mathbb{R}^n) \subseteq \{ x^* \in \mathbb{R}^n : \langle \nabla \phi(x) , x- x^* \rangle \geq 0, \forall x\in \mathbb{R}^n \}. \end{array} \end{aligned} $$
Therefore, given $$ x\in \mathbb {R}^n $$ , we can immediately eliminate the strict half space
$$\displaystyle \begin{aligned} \begin{array}{rcl} \{ x^* \in \mathbb{R}^n : \langle \nabla \phi(x) , x- x^* \rangle &lt; 0 \}. \end{array} \end{aligned} $$
So one needs to check, given any $$ x\in \mathbb {R}^n$$ , the cut at x is given by the hyperplane
$$\displaystyle \begin{aligned} \begin{array}{rcl} H^{\phi}_{x} = \{ z \in \mathbb{R}^n : \langle \nabla \phi(x) , x- z \rangle =0 \}. \end{array} \end{aligned} $$
This is a very important approach in convex optimization, see for example the fundamental paper by Kelley [15]. Following the idea of the cutting plane method, Beck and Sabach introduces the following set whose motivation will be clear as we go along.
$$\displaystyle \begin{aligned} \begin{array}{rcl} Q_{M,\alpha,x} = \{ z\in \mathbb{R}^n : \langle G_M(x), x-z \rangle \geq \frac{1}{\alpha M}\| G_M(x)\|{}^2 \}. \end{array} \end{aligned} $$
If $$ C = \mathbb {R}^n $$ , then
$$\displaystyle \begin{aligned} \begin{array}{rcl} Q_{M,\alpha,x} = \{ z\in \mathbb{R}^n : \langle \nabla g(x), x-z \rangle \geq \frac{1}{\alpha M}\| \nabla g(x)\|{}^2 \}. \end{array} \end{aligned} $$
This is what they refer to as deep cuts and play a fundamental role in their algorithm which we describe below. The first algorithm considers the fact that the Lipschitz constant of ∇g is known. As before let us call the Lipschitz constant as L > 0. Here is the algorithm.
The Minimal Norm Gradient Algorithm (Lipschitz Constant Known)

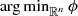  • Step 0: Let L > 0 be the Lipschitz constant of ∇g. Let x 0= prox-center of ϕ = ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq185_HTML.gif.

  • Step 1: For k = 1, 2, ⋯
    $$\displaystyle \begin{aligned} \begin{array}{rcl} x^k = \mbox{sol}(\phi, Q^k \cap W^k ), \end{array} \end{aligned} $$
    where
    $$\displaystyle \begin{aligned} \begin{array}{rcl} Q^k = Q_{L,\beta,x^{k-1}} \end{array} \end{aligned} $$
    and
    $$\displaystyle \begin{aligned} \begin{array}{rcl} W^k = \{ z\in \mathbb{R}^n : \langle \nabla w(x^{k-1}), z-x^{k-1} \rangle \geq 0 \}. \end{array} \end{aligned} $$
Set $$ \beta = \frac {4}{3}$$ if $$ C \neq \mathbb {R}^n $$ and β = 1 if $$ C = \mathbb {R}^n $$ .
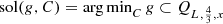The reason for setting $$ \beta = \frac {4}{3}$$ when $$ C \neq \mathbb {R}^n $$ i.e. $$ C \subset \mathbb {R}^n $$ is that ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq192_HTML.gif and if $$ C = \mathbb {R}^n ,\ \beta = 1$$ as $$ \mbox{sol}(g, \mathbb {R}^n ) \subset Q_{L, 1, x }$$ . These facts are proved in Lemma 2.3 and Lemma 2.4 in Beck and Sabach [1]. In Lemma 2.3 in [1], it is shown that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle G_L(x) - G_L(y), x-y \rangle \geq \frac{3}{4L} \| G_L(x) - G_L(y) \|{}^2. \end{array} \end{aligned} $$
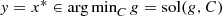If we set ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq195_HTML.gif, then G L(x ∗) = 0 and hence
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \langle G_L(x), x- x^* \rangle \geq \frac{3}{4L} \| G_L(x) \|{}^2. \end{array} \end{aligned} $$
(9.3.17)
Thus $$ x^* \in Q_{L, \frac {4}{3}, x }$$ . Since ∇g is Lipschitz continuous with constant L, then from [1] we see that
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle \nabla g(x) - \nabla g(y), x-y \rangle \geq \frac{1}{L} \| \nabla g(x) - \nabla g(y) \|{}^2. \end{array} \end{aligned} $$
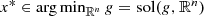Putting y = x ∗, where ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq197_HTML.gif, we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle \nabla g(x), x- x^* \rangle \geq \frac{1}{L} \| \nabla g(x) \|. \end{array} \end{aligned} $$
This shows that
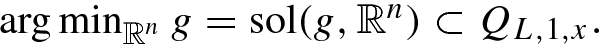
../images/480569_1_En_9_Chapter/480569_1_En_9_Equy_HTML.png
If we do not have any knowledge of the Lipschitz constant of ∇g, then we use an Armijo type criteria in the Minimal norm gradient algorithm that we state here.
The Minimal Norm Gradient Algorithm (Lipschitz Constant is Not Known)

  • Step 0: Initialization: x 0= prox-center of ϕ = 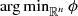../images/480569_1_En_9_Chapter/480569_1_En_9_IEq198_HTML.gif. Take L 0 > 0, η > 1.

  • Step 1: For k = 1, 2, ⋯
    1. (a)
      Find the smallest non-negative integer i k such that $$ \bar {L} = \eta ^{i_k} L_{k-1} $$ and the following inequality
      $$\displaystyle \begin{aligned} \begin{array}{rcl} f(P_{\bar{L}} (x^{k-1})) &amp;\displaystyle \leq&amp;\displaystyle f(x^{k-1}) + \langle \nabla f(x^{k-1}), P_{\bar{L}} (x^{k-1}) - x^{k-1} \rangle \\ &amp;\displaystyle +&amp;\displaystyle \frac{\bar{L}}{2} \| P_{\bar{L}} (x^{k-1}) - x^{k-1} \|{}^2 \end{array} \end{aligned} $$

      is satisfied. Then set $$ L_k := \bar {L}$$

       
    2. (b)
      Set x k = sol(ϕ, Q k ∩ W k), where
      $$\displaystyle \begin{aligned} \begin{array}{rcl} Q^k = Q_{L_k,2,x^{k-1}} \quad \mbox{and} \quad W^k = \{ z\in \mathbb{R}^n : \langle \nabla \phi(x^{k-1}), z-x^{k-1} \rangle \geq 0 \}. \end{array} \end{aligned} $$
       
We shall now show that $$ \mbox{sol(g,C)} \subseteq Q_{\bar {L},2,x}$$ . It has been demonstrated in Lemma 2.5 in Beck and Sabach [1] that if
$$\displaystyle \begin{aligned} \begin{array}{rcl} g(P_{\bar{L}} (x)) \leq g(x) + \langle \nabla g(x), P_{\bar{L}} (x) - x \rangle + \frac{\bar{L}}{2} \| P_{\bar{L}} (x) - x \|{}^2, \end{array} \end{aligned} $$
then for any x ∗∈sol(g,C), one has
$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle G_M(x), x- x^* \rangle \geq \frac{1}{2\bar{L}} \| G_M(x) \|{}^2 \end{array} \end{aligned} $$
and thus $$ \mbox{sol(g,C)} \subseteq Q_{\bar {L},2,x}$$ .
Beck and Sabach [1] also shows that whichever form of the minimal norm gradient algorithm is used one has
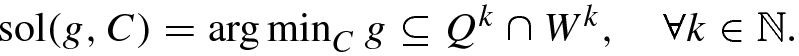
../images/480569_1_En_9_Chapter/480569_1_En_9_Equz_HTML.png
We will now state below the result of Beck and Sabach [1], describing the convergence of the minimum norm gradient algorithm.
Theorem 9.3.3
Consider the (SBP-1) problem and let {x k} be a sequence generated by any of the two forms of the minimum norm gradient algorithm. Then
  1. (a)

    {x k} is bounded.

     
  2. (b)
    for any $$ k \in \mathbb {N} ,$$
    $$\displaystyle \begin{aligned} \begin{array}{rcl} D_{\phi} (x^k, x^{k-1}) + D_{\phi} (x^{k-1}, x^0 ) \leq D_{\phi} (x^k, x^0). \end{array} \end{aligned} $$
     
  3. (c)

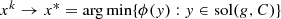    ../images/480569_1_En_9_Chapter/480569_1_En_9_IEq204_HTML.gifi.e. x ∗is a solution of (SBP-1). △

     
Keeping in view our chronological approach to the development of algorithms for simple bilevel programming, we shall end this section by discussing the work of Sabach and Shtern [20], which appeared in 2017 and is in some sense a generalization of Beck and Sabach [1]. The problem they consider is the following
$$\displaystyle \begin{aligned} \begin{array}{rcl} &amp;\displaystyle &amp;\displaystyle \min \phi (x)\\ &amp;\displaystyle &amp;\displaystyle \mbox{subject to } x\in S, \end{array} \end{aligned} $$
where $$ \phi : \mathbb {R}^n \rightarrow \mathbb {R} $$ is a strongly convex function and
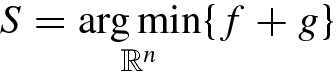
../images/480569_1_En_9_Chapter/480569_1_En_9_Equaa_HTML.png
where f is continuously differentiable and g is an extended-valued proper lower semi-continuous convex function. We shall call this problem (SBP-2). In fact strictly speaking we should consider this problem under the category of non-smooth simple bilevel problems since g can be non-smooth. However we are discussing this problem in this section since we view (SBP-2) as a generalization of (SBP-1). Observe that if we choose g = δ C, where δ C is the indicator function of a closed convex set C, then (SBP-2) reduces to (SBP-1). Those readers who are aware of the algorithms of convex optimization might guess that a proximal gradient type approach needs to be used for solving (SBP-2). Indeed Sabach and Shtern [20], does develop an algorithm based on the prox-mapping. It is important to realize that since ϕ is strongly convex, (SBP-2) also has a unique minimizer which we may mark as x ∗. In fact the method developed in [20], called BiG-SAM, is simpler and cheaper compared than the Minimal Norm Gradient (MNG) method of Beck and Sabach [1]. In the Big-SAM method one needs to compute ∇ϕ only, while in the (MNG) method one needs to compute ∇ϕ and also to minimize ϕ to compute the prox-center.

In Sabach and Shtern [20], the following assumptions are made

  1. (1)

    f has Lipschitz-gradient, i.e. ∇f is Lipschitz on $$ \mathbb {R}^n $$ with Lipschitz constant L f.

     
  2. (2)

    S ≠ ∅.

     
One of the key approaches to solve the lower-level problem in (SBP-2) is the proximal gradient approach which depends on the prox-mapping. Given $$ h : \mathbb {R}^n \rightarrow \mathbb {R} \cup \{ + \infty \} $$ , a proper lower semi-continuous prox-mapping is given as
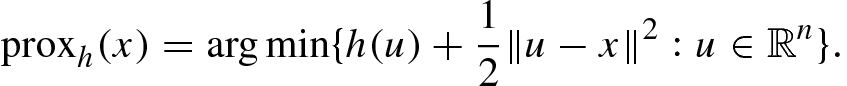
../images/480569_1_En_9_Chapter/480569_1_En_9_Equab_HTML.png
The proximal point algorithm generates the iterates for the lower level problem using the following scheme
$$\displaystyle \begin{aligned} x^{k+1} = \mbox{prox}_{tg} (x^k - t \nabla f (x^k)), \end{aligned}$$
where t > 0 is the step-size. If we set
$$\displaystyle \begin{aligned} P_t(x) = \mbox{prox}_{tg} (x- t \nabla f(x)), \end{aligned}$$
then x is a solution of the lower level problem if and only if x = P t(x). Further P t(x) is also non-expansive (see for example Lemma 1 in [22]). In [22], it is also assumed that the strongly convex upper level objective ϕ has a modulus ρ > 0 and also a Lipschitz gradient on $$ \mathbb {R}^n $$ , whose Lipschitz constant is given as L ϕ. We are now in a position to state the Big-SAM method.
BiG-SAM Method [20]

  • Step 0: Initialization: $$ t \in (0, \frac {1}{L_f}] ,\ \beta \in (0, \frac {2}{L_{\phi }+ \rho }) $$ and {α k} is a sequence satisfying α k ∈ (0, 1], for all $$ k \in \mathbb {N} $$ ; $$ \lim \limits _{k \rightarrow \infty } \alpha _k = 0 $$ and $$ \sum \limits _{k=1}^{\infty } \alpha _k = \infty $$ and $$ \lim \limits _{k \rightarrow \infty } \frac {\alpha _k +1}{\alpha _k} = 1 $$ .Set $$ x^0 \in \mathbb {R}^n $$ as the initial guess solution.

  • Step 1: For k = 1, 2, ⋯ , do
    1. (i)

      y k+1 = proxtg(x k − t∇f(x k))

       
    2. (ii)

      z k+1 = x k − β∇ϕ(x k)

       
    3. (iii)

      x k+1 = α kz k + (1 − α k)y k.

       
The key result regarding the Big-SAM method, is given in Proposition 5 in [20] which says the iterates {x k} generated by this method converge to a point $$ \tilde {x} \in S $$ such that
$$\displaystyle \begin{aligned} \langle \nabla \phi (\tilde{x}), x- \tilde{x} \rangle \geq 0, \quad \forall x \in C \end{aligned}$$
showing that $$ \tilde {x} $$ solves (SBP-2) and hence $$ \tilde {x} = x^* $$ . Here BiG-SAM means Bilevel gradient sequential averaging method, where the sequential averaging is reflected in (iii) of Step 1 in the above algorithm.

Very recently a modification of the BiG-SAM method was presented in [21].

9.4 Algorithms for Non-smooth Data

There are not many algorithmic analysis of the (SBP) problem in the literature and of course for the non-smooth (SBP) problem the situation is not better. The bundle method for non-smooth (SBP) problem presented by Solodov [23] is one of the initial work in this direction. He considered an (SBP) problem with both the upper and lower level objective function to be non-smooth and the lower level problem is unconstrained. The (SBP) problem considered by Solodov in [23] is given as
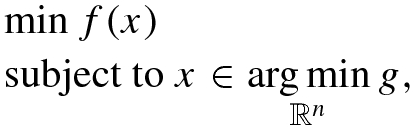
../images/480569_1_En_9_Chapter/480569_1_En_9_Equ116_HTML.png
(9.4.1)
where $$ f, g : \mathbb {R}^n \rightarrow \mathbb {R} $$ are non-smooth convex functions. The main idea behind the algorithm presented in [23] is to minimize the penalized function
$$\displaystyle \begin{aligned} \begin{array}{rcl} \varphi_{\varepsilon} (x) = g(x) + \varepsilon f(x) \end{array} \end{aligned} $$
over $$ \mathbb {R}^n $$ . As ε ↓ 0, the solutions of the problem
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \min \varphi_{\varepsilon}(x) \quad \mbox{subject to } x\in \mathbb{R}^n \end{array} \end{aligned} $$
(9.4.2)
tend to the solution of the (SBP) problem (9.4.1). But it is almost impossible to calculate the solution of (9.4.2) exactly. To avoid that, Solodov’s idea was to make one step in the descent direction of the function $$ \varphi _{\varepsilon _k} $$ from the k-th iteration x k and then update ε k to ε k+1 and repeat the step. To realize the descent step Solodov considered the bundle method for unconstrained non-smooth optimization problem (see [16]). Also we will need ε-subdifferential to discuss the algorithm which we present here.
The ε-subdifferential of $$f,\ \partial _{\varepsilon }f: \mathbb {R}^n \rightrightarrows \mathbb {R}^n$$ , is defined as
$$\displaystyle \begin{aligned} \partial _{\varepsilon }{f}(x)=\{v\in \mathbb{R}^n\; :\; f(y)\geq f(x)+\langle v,y-x\rangle - \varepsilon ,\,\forall \,y\in \mathbb{R}^n \}. \end{aligned}$$
The idea of a bundle method is to store information of the past in a bundle. At any k-th step let x k be the iteration point and y i (i = 1, 2, ⋯ , l − 1) are the points generated by the algorithm so far. Note that all y i’s may not be accepted as the iteration point in the process. Which means there may be some y i’s which are not included in the sequence {x k}. The information about all the y i (i = 1, 2, ⋯ , l − 1), such as the subgradient and some quantities required in this algorithm are stored in the bundle. Note that $$ \{ x^n \}_{n=1}^ {k}$$ is actually a finite subsequence of the finite sequence $$ \{ y^i \}_{i=1}^ {l-1}$$ . Let there be l iterations before we choose to modify x k and ε k, then k(l) is the index of the last iteration and k = k(l). Let ξ i ∈ ∂f(y i) and ζ i ∈ ∂g(y i). Then $$ \varepsilon _k \xi ^i + \zeta ^i \in \partial \phi _{\varepsilon _k} (y^i) $$ . In the bundle method, a linearisation of the function $$ \varphi _{\varepsilon _k} $$ is used (see for example [16]). Then $$ \varphi _{\varepsilon _k}(x) $$ can be approximated by the following function
$$\displaystyle \begin{aligned} \begin{array}{rcl} \psi(x):= \max \{ \varphi_{\varepsilon_k}(x^k) + \langle w^k, x- x^k \rangle : w^k \in \partial \varphi_{\varepsilon_k}(x^k)\}. \end{array} \end{aligned} $$
But this includes the calculation of all the subgradients of $$ \varphi _{\varepsilon _k} $$ at x k, which is again a tough job. So the following cutting-planes approximation ψ l is used by Solodov of the function $$ \varphi _{\varepsilon _k} $$ .
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \psi_{l}(x):= \max\limits_{i&lt;l} \{ \varepsilon_k f(y^i) + g(y^i) + \langle \varepsilon_k \xi^i + \zeta^i, x- y^i \rangle \}. \end{array} \end{aligned} $$
(9.4.3)
This is a linearisation centred at y i. To reduce the storage requirements the following expression is constructed, which is centred at x k.
$$\displaystyle \begin{aligned} \psi_{l}(x):=&amp; \max\limits_{i&lt;l} \{ \varepsilon_k f(x^k) + g(x^k) + \langle \varepsilon_k \xi^i + \zeta^i, x- x^k \rangle\\ &amp; - \varepsilon_k [ f(x^k) - f(y^i) - \langle \xi^i, x^k - y^i \rangle ] - [ g(x^k) - g(y^i) - \langle \zeta^i, x^k - y^i \rangle]\}\\ =&amp; \varepsilon_k f(x^k) + g(x^k) + \max\limits_{i&lt;l} \{ - \varepsilon_k e^{k,i}_{f} - e^{k,i}_{g} + \langle \varepsilon_k \xi^i + \zeta^i, x- x^k \rangle \} \end{aligned}$$
where
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} e^{k,i}_{f} = f(x^k) - f(y^i) - \langle \xi^i, x^k - y^i \rangle \end{array} \end{aligned} $$
(9.4.4)
and
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} e^{k,i}_{g} = g(x^k) - g(y^i) - \langle \zeta^i, x^k - y^i \rangle. \end{array} \end{aligned} $$
(9.4.5)
Clearly, by convexity of f and g; $$e^{k,i}_{f},e^{k,i}_{g} \geq 0 $$ . Now as ξ i ∈ ∂f(y i), for any $$ x \in \mathbb {R}^n $$ we have
$$\displaystyle \begin{aligned} \begin{array}{rcl} f(x) &amp;\displaystyle \geq&amp;\displaystyle f(y^i) + \langle \xi^i , x- y^i \rangle\\ &amp;\displaystyle =&amp;\displaystyle f(x^k) + \langle \xi^i , x- x^k \rangle - e^{k,i}_{f}. \end{array} \end{aligned} $$
This implies that $$ \xi ^i \in \partial _{e^{k,i}_f} f(x^k) $$ . Similarly, $$ \zeta ^i \in \partial _{e^{k,i}_g} g(x^k) $$ . Then
$$\displaystyle \begin{aligned} \varepsilon_k \xi^i + \zeta^i \in \partial_{(\varepsilon_k e^{k,i}_f + e^{k,i}_g)} \varphi_{\varepsilon_k}(x^k). \end{aligned}$$
Choose μ l > 0, then the minimizer of the following convex optimization problem
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \min\limits_{x\in \mathbb{R}^n} \big\{ \psi_l(x) + \frac{\mu_l}{2} \| x- x^k \|{}^2 \big\} \end{array} \end{aligned} $$
(9.4.6)
can be taken as the next candidate point y l. Note that (9.4.6) has unique solution since the objective function is strongly convex. If $$ \varphi _{\varepsilon _k} (y^l) $$ is sufficiently small compared with $$ \varphi _{\varepsilon _k} (x^k) $$ , then y l is considered to be a serious (or acceptable) step and x k+1 := y l. In fact y l is considered to be a serious step if the following decrease criteria holds, i.e.
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \varphi_{\varepsilon_k} (y^l) \leq \varphi_{\varepsilon_k} (x^k) - \gamma \delta_l. \end{array} \end{aligned} $$
(9.4.7)
For γ ∈ (0, 1), let
$$\displaystyle \begin{aligned} \begin{array}{rcl} \delta_l = \hat{\varepsilon}^{k,l} + \frac{1}{2\mu_l} \| \hat{g}^l \|{}^2, \end{array} \end{aligned} $$
with,
$$\displaystyle \begin{aligned} \begin{array}{rcl} &amp;\displaystyle &amp;\displaystyle \hat{\varepsilon}^{k,l} = \varphi_{\varepsilon_k} (x^k) - \varphi_{\varepsilon_k} (y^l) - \frac{1}{\mu_l} \| \hat{g}^l \|{}^2,\\ &amp;\displaystyle &amp;\displaystyle \hat{g}^l = \mu_l (x^k - y^l). \end{array} \end{aligned} $$
Therefore,
$$\displaystyle \begin{aligned} \delta_l = \varphi_{\varepsilon_k} (x^k) - \varphi_{\varepsilon_k} (y^l) - \frac{\mu_l}{2} \| x^k - y^l \|{}^2.\end{aligned} $$
We can see that δ l deals with the difference in the functional values of $$ \varphi _{\varepsilon _k} $$ at x k and y l and also keeps the distance between x k and y l into account. Note that δ l ≥ 0 as $$\hat {\varepsilon }^{k,l} \geq 0$$ , which is shown in Lemma 2.1 [23]. If y l does not satisfy the condition (9.4.7), then y l is considered as a null step and is not included in the sequence of iterates. But this null step then contributes to construct a better approximation ψ l+1 of the function $$ \varphi _{\varepsilon _k} $$ using (9.4.3). Then y l+1 is generated using (9.4.6) with μ l+1 > 0, which can again be a serious step or a null step. The process is continued until x k+1 is generated.
Let us now discuss a little about bundles, where the information about the candidate points y l (no matter serious step or null step) is stored. In [23], Solodov describes an efficient way to store all the information needed for the bundle method algorithm and also ensures that the number of elements in the bundles is under some pre-decided bound. Managing the bundle this way keeps the algorithm computationally more suitable and efficient. Solodov [23] has divided the information at any iteration l into two parts, one is called oracle bundle denoted by $$ B^{oracle}_l $$ and another one is aggregate bundle, $$ B^{agg}_l $$ . Both the bundles contain approximated subgradients of the objective functions f and g at x k and are defined in the following way.
$$\displaystyle \begin{aligned} B^{oracle}_l \subset \bigcup_{i&lt;l} \left\{ e^{k,i}_f, e^{k,i}_g \in \mathbb{R}_{+},\xi^i \in \partial_{e^{k,i}_f} f(x^k), \zeta^i \in \partial_{e^{k,i}_g} g(x^k) \right\}\end{aligned} $$
and
$$\displaystyle \begin{aligned} B^{agg}_l \subset \bigcup_{i&lt;l} \left\{ \hat{\varepsilon}^{k,i}_f,\hat{\varepsilon}^{k,i}_g \in \mathbb{R}_{+},\hat{\xi}^i \in \partial_{\hat{\varepsilon}^{k,i}_f} f(x^k), \hat{\zeta}^i \in \partial_{\hat{\varepsilon}^{k,i}_g} g(x^k) \right\},\end{aligned} $$
where $$e^{k,i}_f,e^{k,i}_g $$ are given by (9.4.4) and (9.4.5) and let us set
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \hat{\varepsilon}^{k,l}_f = \sum_{i \in B^{oracle}_l} \lambda^l_i e^{k,i}_f + \sum_{i \in B^{agg}_l} \hat{\lambda}^l_i \hat{\varepsilon}^{k,i}_f, \end{array} \end{aligned} $$
(9.4.8)
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \hat{\varepsilon}^{k,l}_g = \sum_{i \in B^{oracle}_l} \lambda^l_i e^{k,i}_g + \sum_{i \in B^{agg}_l} \hat{\lambda}^l_i \hat{\varepsilon}^{k,i}_g, \end{array} \end{aligned} $$
(9.4.9)
with $$ \lambda ^l_i, \hat {\lambda }^l_i \geq 0 $$ and $$ \sum _{i \in B^{oracle}_l} \lambda ^l_i + \sum _{i \in B^{agg}_l} \hat {\lambda }^l_i = 1 $$ .
Note that ξ i ∈ ∂f(y i) and ζ i ∈ ∂g(y i), so we can see that the bundle $$ B^{oracle}_l $$ stores the subgradient information of the objective functions at some candidate points y i. But there may not be any candidate point y j, j < l such that $$ \hat {\xi }^j \in \partial f (y^j)$$ and $$ \hat {\zeta }^j \in \partial g (y^j)$$ . Also note that the construction of $$\hat {\varepsilon }^{k,l}_f $$ and $$ \hat {\varepsilon }^{k,l}_g $$ justifies the term aggregate bundle. Even though the bundles $$ B^{oracle}_l $$ and $$ B^{agg}_l $$ do not restore all the subgradients at all the candidate points, still a cutting-plane approximation of $$ \varphi _{\varepsilon _k}$$ can be done using these bundle information which is given by
$$\displaystyle \begin{aligned} \psi_{l}(x):= &amp;\varepsilon_k f(x^k) + g(x^k) \\ +\max &amp; \left\{ \max\limits_{i \in B^{oracle}_l} \left\{ -(\varepsilon_k e^{k,i}_{f} + e^{k,i}_{g}) + \langle \varepsilon_k \xi^i + \zeta^i, x- x^k \rangle \right\}\right., \\ &amp; \left.\max\limits_{i \in B^{agg}_l} \left\{ -(\varepsilon_k \hat{\varepsilon}^{k,i}_{f} + \hat{\varepsilon}^{k,i}_{g}) + \langle \varepsilon_k \hat{\xi}^i + \hat{\zeta}^i, y- x^k \rangle \right\} \right\} \end{aligned} $$
(9.4.10)
As we can see the two approximations (9.4.3) and (9.4.10) of the penalized function $$ \varphi _{\varepsilon _k} $$ are different. The connection between these two approximations are well established in terms of the solution of the problem given in (9.4.6) and the function (9.4.10) in the following lemma (Lemma 2.1, [23]).
Lemma 9.4.1
Let y lbe the solution of (9.4.6) with ψ l, as given in (9.4.10). Then

  • $$ y^l = x^k - \frac {1}{\mu ^l} (\varepsilon _k \hat {\xi }^l + \hat {\zeta }^l )$$ .

  • $$\hat {\xi }^l = \sum _{i \in B^{oracle}_l} \lambda ^l_i \xi ^i + \sum _{i \in B^{agg}_l} \hat {\lambda }^l_i \hat {\xi }^i $$ $$\hat {\zeta }^l = \sum _{i \in B^{oracle}_l} \lambda ^l_i \zeta ^i + \sum _{i \in B^{agg}_l} \hat {\lambda }^l_i \hat {\zeta }^i $$ ,where $$ \lambda ^l_i, \hat {\lambda }^l_i \geq 0 $$ and $$ \sum _{i \in B^{oracle}_l} \lambda ^l_i + \sum _{i \in B^{agg}_l} \hat {\lambda }^l_i = 1 $$ .

  • $$\varepsilon _k \hat {\xi }^l + \hat {\zeta }^l \in \partial \psi _l (y^l)$$ .

  • $$ \hat {\xi }^l \in \partial _{\hat {\varepsilon }^{k,l}_{f}} f(x^k),\ \hat {\zeta }^l \in \partial _{\hat {\varepsilon }^{k,l}_{g}} g(x^k) $$ , where $$\hat {\varepsilon }^{k,l}_{f} $$ and $$\hat {\varepsilon }^{k,l}_{g} $$ are from (9.4.8) and (9.4.9).

  • $$ \varepsilon _k \hat {\xi }^l + \hat {\zeta }^l = \hat {g}^l \in \partial _{\hat {\varepsilon }^{k,l}} \varphi _{\varepsilon _k} (x^k) $$ , where $$ \hat {\varepsilon }^{k,l} = \varepsilon _k \hat {\varepsilon }^{k,l}_{f} + \hat {\varepsilon }^{k,l}_{g} $$ .

  • $$ \hat {\varepsilon }^{k,l} = \varphi _{\varepsilon _k} (x^k) - \varphi _{\varepsilon _k} (y^l) - \frac {1}{\mu _l} \| \hat {g}^l \|{ }^2 \geq 0 $$ . △

Here note that λ l and $$ \hat {\lambda }^l $$ in Lemma 9.4.1 are obtained as a part of subgradient calculation of ψ l while solving the strongly convex optimization problem (9.4.6). We have already mentioned that Solodov [23] has developed two different bundles to maintain the bundle size under a fixed limit. Here we discuss how that is done. Let the maximum size that the bundle can attain together be |B|max. So at any l-th step, if
$$\displaystyle \begin{aligned} |B^{oracle}_{l} \cup B^{agg}_{l} |= |B|{}_{max} , \end{aligned}$$
then at least two elements are removed from $$ B^{oracle}_{l+1}\cup B^{agg}_{l+1} $$ and the aggregate information $$ ( \hat {\varepsilon }^{k,l}_{f},\hat {\varepsilon }^{k,l}_{g}, \hat {\xi }^l, \hat {\zeta }^l )$$ is included in $$ B^{agg}_{l} $$ and renamed as $$ B^{agg}_{l+1} $$ . Also include $$ ( e^{k,l}_{f},e^{k,l}_{g}, \xi ^l, \zeta ^l )$$ in $$ B^{oracle}_{l}$$ and called $$ B^{oracle}_{l+1}$$ . Now using the bundle information, Solodov constructed the following relations which satisfies all the results mentioned in Lemma 9.4.1.
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \mbox{For } i \in B^{oracle}_{l+1}, &amp;\displaystyle &amp;\displaystyle e^{k+1,i}_f = e^{k,i}_f + f(x^{k+1}) - f(x^k) + \langle \xi^i , x^k - x^{k+1} \rangle, \\ &amp;\displaystyle &amp;\displaystyle e^{k+1,i}_g = e^{k,i}_g + g(x^{k+1}) - g(x^k) + \langle \zeta^i , x^k - x^{k+1} \rangle\\ \mbox{and for } i \in B^{oracle}_{l+1}&amp;\displaystyle &amp;\displaystyle \hat{\varepsilon}^{k+1,i}_f =\hat{\varepsilon}^{k,i}_f + f(x^{k+1}) - f(x^k) + \langle \hat{\xi}^i , x^k - x^{k+1} \rangle, \\ &amp;\displaystyle &amp;\displaystyle \hat{\varepsilon}^{k+1,i}_g = \hat{\varepsilon}^{k,i}_g + g(x^{k+1}) - g(x^k) + \langle \hat{\zeta}^i , x^k - x^{k+1} \rangle \quad .\qquad \qquad \end{array} \end{aligned} $$
(9.4.11)
Now we are ready to present the algorithm for (SBP) problem.
Bundle Method Algorithm: [23]

  • Step 0: Choose m ∈ (0, 1), an integer $$ | B|{ }_{max} \geq 2 ,\ x^0 \in \mathbb {R}^n ,\ \varepsilon _0 &gt; 0 $$ and β 0 > 0.Set y 0 := x 0 and compute f(y 0), g(y 0), ξ 0 ∈ ∂f(y 0), ζ 0 ∈ ∂g(y 0).Set $$ k=0 , l= 1, e^{0,0}_f = e^{0,0}_g := 0 $$ .Define $$ B^{oracle}_l:= \{ (e^{0,0}_f, e^{0,0}_g, \xi ^0,\zeta ^0 )\} $$ and $$ B^{agg}_l:= \emptyset $$

  • Step 1: At any l-th step, choose μ l > 0 and compute y l as the solution of (9.4.6) with ψ l, as given in (9.4.10).Compute f(y l), g(y l), ξ l ∈ ∂f(y l), ζ l ∈ ∂g(y l) and $$ e^{k,l}_f, e^{k,l}_g $$ using (9.4.4) and (9.4.5).

  • Step 2: If $$ \varphi _{\varepsilon _k} (y^l) \leq \varphi _{\varepsilon _k} (x^k) - m \delta _l $$ , then y l is a serious step, otherwise null step.

  • Step 3: Check if $$ |B^{oracle}_{l} \cup B^{agg}_{l} |&lt; |B|{ }_{max} $$ , otherwise manage the bundle as mentioned earlier.

  • Step 4: If y l is a serious step, then set x k+1 := y l.Choose 0 < ε k+1 < ε k and 0 < β k+1 < β k. Update $$e^{k+1,i}_f, e^{k+1,i}_g, \hat {\varepsilon }^{k+1,i}_f, \hat {\varepsilon }^{k+1,i}_g $$ using (9.4.11).Set k = k + 1 and go to Step 5. If $$ \max { \hat {\varepsilon }^{k,l}, \| \hat {g}^l \|} \leq \beta _k \varepsilon _k $$ , choose 0 < ε k+1 < ε k and 0 < β k+1 < β k. Set x k+1 := x k, k = k + 1 and go to step 5.

  • Step 5: Set l = l + 1 and go to Step 1.

Note that $$ \max { \hat {\varepsilon }^{k,l}, \| \hat {g}^l \|} \leq \beta _k \varepsilon _k $$ works as a stopping criteria to minimize the function ψ k. The convergence result of this algorithm is presented through the following theorem from [23].

Theorem 9.4.2
Let $$ f, g: \mathbb {R}^n \rightarrow \mathbb {R} $$ are convex functions such that f is bounded below on $$ \mathbb {R}^n $$ and the solution set of the (SBP) problem S is non-empty and bounded. Let us choose μ l, ε k, β ksuch that the following conditions are satisfied at any $$ l, k \in \mathbb {N}$$ .
  1. 1.
    μ l+1 ≤ μ land there exists $$ \hat {\mu },\bar {\mu } &gt;0 $$ such that
    $$\displaystyle \begin{aligned} 0&lt; \hat{\mu} \leq \mu_l \leq \bar{\mu}. \end{aligned}$$
     
  2. 2.

    ε k → 0 as k → 0 and $$ \sum _{k=0}^{\infty } \varepsilon _k = + \infty $$ .

     
  3. 3.

    β k → 0 as k → 0.

     

Then dist(x k, S) → 0 as k → 0. This also implies that any accumulation point of the sequence {x k} is a solution of the (SBP) problem. △

Another algorithm is proposed by Dempe et al. [8] for the non-smooth simple bilevel programming problem. In [8], we present an algorithm for the (SBP) problem in more general scenario than that we have discussed so far. Note that in [23], the considered (SBP) problem is unconstrained in the lower level, whereas the (SBP) problem we consider, which given below, has constrained lower level problem.
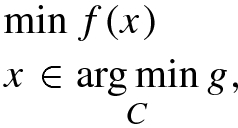
../images/480569_1_En_9_Chapter/480569_1_En_9_Equan_HTML.png
where $$ f, g : \mathbb {R}^n \rightarrow \mathbb {R} $$ are continuous, convex functions and $$ C \subseteq \mathbb {R}^n $$ is closed, convex set. Our algorithm is inspired from the penalisation approach by Solodov [22]. But our algorithm is different from Solodov’s approach in two aspects, one is that we don’t assume any differentiability assumption on the upper and lower level objective functions which naturally helps us to get rid of the Lipschitz continuity assumption on the gradient of the objective functions that is made by Solodov [22], another one is the fact that our algorithm is based on proximal point method whereas Solodov’s algorithm is based on projected gradient method. Our Algorithm is also inspired by Cabot [2] and Facchinei et al. [11] but again different in the sense that our algorithm deals with more general form of (SBP) compared with those. The only assumption we make is that the solution set of the (SBP) problem needs to be non-empty and bounded. This is done to ensure the boundedness of the iteration points which will finally lead to the existence of an accumulation point and hence a solution of the (SBP) problem.

In the proximal point algorithm that we present, we consider an approximate solution rather than the exact solution. For this purpose we need to use ε- subdifferential and ε-normal cone for ε > 0. We have already presented the ε-subdifferential while discussing the last algorithm. Here we present the ε-normal set.

The ε-normal set of $$ C \subseteq \mathbb {R}^n $$ is defined as
$$\displaystyle \begin{aligned} \begin{array}{rcl} N_C^{\varepsilon}(x)= \{v \in \mathbb{R}^n: \langle v, y- x\rangle \leq \varepsilon, \quad \forall y \in C\}. \end{array} \end{aligned} $$
Consider the following sequence of penalized functions
$$\displaystyle \begin{aligned} \varphi = g + \varepsilon_k f. \end{aligned}$$
We aim to minimize this function approximately over the constraint set C to obtain the iteration point at any (k + 1)-st step. Let η k > 0 and λ k > 0, then the (k + 1)-st iterate comes from the following relation.
$$\displaystyle \begin{aligned} x^{k+1} \in \eta_k \mbox{-argmin}_C \{ \varphi_k + \frac{1}{2\lambda_k} \|.- x^k \|{}^2 \} \end{aligned}$$
Considering the optimality condition for this approximate minimization problem we get our key step to design the algorithm (for details see [8]), which is given as
$$\displaystyle \begin{aligned} -\frac{1}{\lambda_k} (x^{k+1} - x^k ) \in \partial_{\eta_k^1} \varphi_k (x^{k+1}) + N^{\eta_k^2}_C (x^{k+1}), \end{aligned}$$
where $$ \eta _k^1 + \eta _k^2 \leq \eta _k $$ . Now we present the algorithm formally.
Algorithm for the (SBP) Problem

  • Step 0. Choose x 0 ∈ C, 𝜖 0 ∈ (0, ∞) and let k := 0.

  • Step 1. Given x k, λ k > 0, ε k > 0 and η k > 0, choose x k+1 ∈ C such that
    $$\displaystyle \begin{aligned} \begin{array}{rcl} -(\frac{x^{k+1}-x^k}{\lambda_k}) \in \partial_{\eta_k^1}(\varphi_k)(x^{k+1}) + N_C^{\eta_k^2}(x^{k+1}) \end{array} \end{aligned} $$
    where $$\eta _k^1, \eta _k^2 \geq 0$$ and $$\eta _k^1 + \eta _k^2 \leq \eta _k$$ .
For the convergence analysis of this algorithm we make the following assumptions on the sequences {ε k}, {λ k} and {η k}. Then the convergence results of this algorithm is presented in the next theorem.

  • {ε k} is a decreasing sequence such that $$\lim \limits _{n \rightarrow \infty } \varepsilon _n = 0$$ and $$\sum \limits _{n=0}^{\infty } \varepsilon _n = + \infty $$ .

  • There exists $$ \underline {\lambda }&gt;0$$ and $$\overline {\lambda }&gt;0$$ such that $$ \underline {\lambda }\leq \lambda _n \leq \overline {\lambda }$$ for all $$n \in \mathbb {N}$$ .

  • $$\sum \limits _{n=0}^{\infty } \eta _n &lt;+\infty $$ .

Theorem 9.4.3 ([8])
Let $$ C\subset \mathbb {R}^n $$ be a non-empty closed convex set, $$g : \mathbb {R}^n \rightarrow \mathbb {R}$$ and $$f : \mathbb {R}^n \rightarrow \mathbb {R}$$ be convex functions. Assume that the functions g and f are bounded below, that the set $$S_0 := \arg \min \limits _C g$$ is nonempty, and that the set $$S_1 := \arg \min \limits _{S_0} f$$ is nonempty and bounded. Let {ε n}, {λ n}, {η n} be nonnegative sequences which satisfy the assumptions mentioned above. Then any sequence {x n} generated by the algorithm satisfies
$$\displaystyle \begin{aligned} \begin{array}{rcl} \lim \limits_{n \rightarrow \infty} d(x^n, S_1)= 0. \end{array} \end{aligned} $$

This also implies that any accumulation point of the sequence {x n}, is a solution of the (SBP) problem. △

The reference [13] in the list of reference was first brought to our notice by M. V. Solodov. In [13], the ε-subgradient is used to develop an inexact algorithmic scheme for the (SBP) problem. however the scheme and convergence analysis developed in [13] is very different from the one in [8]. It is important to note that in contrast to the convergence analysis in [8], the scheme in [13] needs more stringent condition. Also an additional assumption is made on the subgradient of the lower level objective (see Proposition 2, [13]). They also considered the case when the upper level objective is smooth and also has Lipschitz gradient.