

The idea of a game mirroring the conflicts of the world is an old one. In the Mabinogion, a collection of Welsh folktales (eleventh to thirteenth centuries), one story has two warring kings playing chess while their armies battle nearby. Each time one king captures a piece, a messenger arrives to inform the other that he has lost a crucial man or division. Finally one king checkmates. A bloody messenger staggers in and tells the loser, “The army is in flight. You have lost the kingdom.”
This fiction refers to the frankly military origins of chess. The Chinese game of go, the Hindu chaturanga, and many other games are battle simulations, too. Those who see games as simulations of war may see war as a kind of game, too. The classic instance of this was Prussia’s century-long infatuation with Kriegspiel.
Devised as an educational game for military schools in the eighteenth century, Kriegspiel was originally played on a board consisting of a map of the French-Belgian frontier divided into a grid of 3,600 squares. Game pieces advanced and retreated across the board like armies.
The original Kriegspiel spawned many imitations and was ultimately supplanted by a version that became popular among Prussian army officers. This used real military maps in lieu of a game board. In 1824 the chief of the German general staff said of Kriegspiel, “It is not a game at all! It’s training for war!”
So began a national obsession that defies belief today. The Prussian high command was so taken with this game that it issued sets to every army regiment. Standing orders compelled every military man to play it. The Kaiser appeared at Kriegspiel tournaments in full military regalia. Inspired by overtly militaristic chess sets then in vogue (pieces were sculpted as German marshals, colonels, privates, etc.), craftsmen produced Kriegspiel pieces of obsessive detail. A pale remnant of these Zinnfiguren (“tin figures”) survives today as toy soldiers. Layer after layer of complexity accreted around the game as its devoted players sought ever greater “realism.” The rule book, originally sixty pages, grew thicker with each edition. Contingencies of play that were once decided by chance or an umpire were referred to data tables drawn from actual combat.
Claims that the game was behind Prussia’s military victories stimulated interest internationally. Prussia’s Kriegspiel dry runs of war with Austria supposedly led to a strategy that proved decisive in the Six Weeks’ War of 1866. After that, the Austrian Army took no chances and began playing Kriegspiel. France’s defeat in the Franco-Prussian War (1870)—allegedly another Kriegspiel victory for Prussia—spawned a Kriegspiel craze there.
Kriegspiel came to the United States after the Civil War. One American army officer complained that the game “cannot be readily and intelligently used by anyone who is not a mathematician, and it requires, in order to be able to use it readily, an amount of special instruction, study, and practice about equivalent to that necessary to acquire a speaking knowledge of a foreign language.” Nonetheless, it eventually became popular in the Navy and at the Naval War College in Newport, Rhode Island.
Japan’s victory in the Russo-Japanese War (1905) was the last credited to a nation’s playing of Kriegspiel. It became apparent that strategies honed in the game did not always work in battle. Germany’s defeat in World War I was a death knell for the game—except, ironically, in Germany itself, where postwar commanders fought each other with tin replicas of the regiments denied them by the Treaty of Versailles.
In Budapest, the young John von Neumann played an improvised Kriegspiel with his brothers. They sketched out castles, highways, and coastlines on graph paper, then advanced and retreated “armies” according to rules. During World War I, Johnny obtained maps of the fronts and followed reports of real advances and retreats. Today Kriegspiel is usually played with three chessboards, visible only to an umpire. In this form it was a popular lunch-hour pastime at the RAND Corporation, and von Neumann played the game on visits there.
To some critics, game theory is the twentieth century’s Kriegspiel, a mirror in which military strategists see reflected their own preconceptions. The comparison is revealing even while being unfair. Game theory did become a kind of strategic oracle, particularly in the two decades after Hiroshima. The problem is one common to oracles, namely that game theory’s answers can depend on exactly how you phrase the questions.
Why a theory of games? It is a cliché of scientific biography to find reasons in a scientist’s personality for choosing a subject. But the question is fair enough. Though the scientist or mathematician is a discoverer rather than a creator, there is a literal universe of avenues to explore. Why one and not another?
Meaningful answers are harder to come by than historians of science like to admit. When the question has been put to living scientists, they are often at a loss for words. Many have noted von Neumann’s fascination with play, his collection of children’s toys, his sometimes childish humor. In this he was not atypical among scientists. Jacob Bronowski wrote (1973), “You must see that in a sense all science, all human thought, is a form of play. Abstract thought is the neoteny1 of the intellect, by which man is able to carry out activities which have no immediate goal (other animals play only while young) in order to prepare himself for long-term strategies and plans.”
Game theory is not about “playing” as usually understood. It is about conflict among rational but distrusting beings. Von Neumann escaped revolution and terrorism in Hungary and later the rise of Nazism. His relationship with Klara was one of repeated conflict. In his letters to his wife Johnny talks of double-crossing, reprisals, and boundless distrust. That’s part of what game theory is about.
Game theory was the brainchild of a cynic. Some commentators have suggested that von Neumann’s personal cynicism influenced the theory. It is conceivable that von Neumann’s personality led him to explore game theory rather than something else. It is wrong to think that von Neumann concocted game theory as a “scientific” basis for his personal beliefs or politics. Game theory is a rigorously mathematical study which evolves naturally from a reasonable way of looking at conflict. Von Neumann would not have pursued game theory had his mathematical intuition not told him that it was a field ripe for development. Some of the mathematics of game theory are closely related to that von Neumann used in treating quantum physics.
The nominal inspiration for game theory was poker, a game von Neumann played occasionally and not especially well. (A 1955 Newsweek article appraised him as “only a fair-to-middling winner” at the game.) In poker, you have to consider what the other players are thinking. This distinguishes game theory from the theory of probability, which also applies to many games. Consider a poker player who naively tries to use probability theory alone to guide his play. The player computes the probability that his hand is better than the other players’ hands, and wagers in direct proportion to the strength of the hand. After many hands, the other players will realize that (say) his willingness to sink twelve dollars in the pot means he has at least three of a kind. As poker players know, that kind of predictability is bad (a “poker face” betrays nothing).
Good poker players do not simply play the odds. They take into account the conclusions other players will draw from their actions, and sometimes try to deceive the other players. It was von Neumann’s genius to see that this devious way of playing was both rational and amenable to rigorous analysis.
Not everyone agreed that game theory was the most fruitful outlet for von Neumann’s ample talents. Paul Halmos, von Neumann’s assistant at Princeton, told me, “As far as I was concerned, he was just wasting his time on ‘that game stuff.’ I know full well that a large part of the world doesn’t agree with the opinions I held then, and I am not sure whether I myself agree with them now, but … I never learned the subject and never learned to like it.”
Von Neumann cannot be given undivided credit for the invention of game theory. Beginning in 1921, seven years before von Neumann’s first paper, French mathematician Emile Borel published several papers on “la théorie du jeu.” The parallels between these papers and von Neumann’s work are strong. Borel used poker as an example and took up the problem of bluffing, just as von Neumann would. Borel appreciated the potential economic and military applications of game theory. Indeed, Borel warned against overly simplistic applications of game theory to warfare. He was not talking off the top of his head. Borel, who had held public office, became minister of the French Navy in 1925. Most important, Borel posed the basic questions of game theory: for what games is there a best strategy, and how does one find such a strategy?
Borel did not develop these issues very far. Like so many creative individuals, von Neumann was jealous of prior claims to “his” innovation. His 1928 paper and the 1944 book make but scant mention of Borel, that in footnotes. Lest there be any doubt, Ulam said that one of Borel’s papers had indeed inspired von Neumann’s work.
Von Neumann’s slighting treatment of Borel long contributed to an underappreciation of the latter’s work. In 1953 von Neumann was reportedly furious to learn that Borel’s papers were being translated into English. The translator, mathematician L. J. Savage, told Steve Heims: “He phoned me from someplace like Los Alamos, very angry. He wrote a criticism of these papers in English. The criticism was not angry. It was characteristic of him that the criticism was written with good manners.”
All this granted, the seminal paper of game theory is without doubt von Neumann’s 1928 article, “Zur Theorie der Gesellschaftspiele” (“Theory of Parlor Games”). In this he proved (as Borel had not) the famous “minimax theorem.” This important result immediately gave the field mathematical respectability.
Von Neumann wanted game theory to reach a larger audience than mathematicians. He felt the developing field would be of most use to economists. He teamed with an Austrian economist then at Princeton, Oskar Morgenstern, to develop his theory.
Von Neumann and Morgenstern’s Theory of Games and Economic Behavior is one of the most influential and least-read books of the twentieth century. Princeton University Press admitted as much in an ad it ran in American Scientist to commemorate the fifth year of anemic sales. “Great books often take a while to achieve recognition.... Then, later, when the world learns about them, their influence far surpasses their readership.” The book had still not quite sold 4,000 copies in five years, a fact that would normally be hard to square with the contention that the book had taken the field of economics by storm. Most economists still hadn’t read it (and never would); it wasn’t even in the libraries of many schools of economics. The ad noted “a few copies bought by professional gamblers.”
Theory of Games and Economic Behavior is a difficult book. Today, the reader’s enthusiasm for plowing through all 641 formula-filled pages is dampened by the fact that von Neumann and Morgenstern got sidetracked in their treatment of games of more than two persons. Their approach, while not wrong, no longer seems the most useful or illuminating one.
If nothing else, the book is ambitious. Von Neumann and Morgenstern dreamed of doing for economics what von Neumann did for quantum physics and could not do for mathematics itself: putting it on an axiomatic basis. The authors stated: “We hope to establish satisfactorily … that the typical problems of economic behavior become strictly identical with the mathematical notions of suitable games of strategy.”
Theory of Games and Economic Behavior thus presents itself as a pioneering work of economics. The book’s introduction is almost apologetic about investigating recreational games. The games are presented as potential models for economic interactions. (Military applications, which were to become so important to von Neumann’s followers, are not mentioned.)
The tone is iconoclastic. Von Neumann and Morgenstern insist that economists must go back to square one. They deride the then-current state of mathematical economics, comparing it with the state of physics before Kepler and Newton. They chide those who advocate economic reform based on presently unconfirmable theories. One gathers the authors were thinking of Marxism, among other theories.
The authors speculate that a future exact science of economics will require its own, yet-unimagined mathematics. They suggest that calculus, which is ultimately derived from the physics of falling and orbiting bodies, is presently overemphasized in mathematics.
Fortunately for our purposes, the essential kernel of game theory is easy to grasp, even for those with little background in—or tolerance for—mathematics. Game theory is founded on a very simple but powerful way of schematizing conflict, and this method can be illustrated by a few familiar childhood games.
Most people have heard of the reputed best way to let two bratty children split a piece of cake. No matter how carefully a parent divides it, one child (or both!) feels he has been slighted with the smaller piece. The solution is to let one child divide the cake and let the other choose which piece he wants. Greed ensures fair division. The first child can’t object that the cake was divided unevenly because he did it himself. The second child can’t complain since he has his choice of pieces.
This homely example is not only a game in von Neumann’s sense, but it is also about the simplest illustration of the “minimax” principle upon which game theory is based.
The cake problem is a conflict of interests. Both children want the same thing—as much of the cake as possible. The ultimate division of the cake depends both on how one child cuts the cake and which piece the other child chooses. It is important that each child anticipates what the other will do. This is what makes the situation a game in von Neumann’s sense.
Game theory searches for solutions—rational outcomes—of games. Dividing the cake evenly is the best strategy for the first child, since he anticipates that the other child’s strategy will be to take the biggest piece. Equal division of the cake is therefore the solution to this game. This solution does not depend on a child’s generosity or sense of fair play. It is enforced by both children’s self-interest. Game theory seeks solutions of precisely this sort.
With this example in mind, let’s go back and examine some of the ideas we have introduced. There are many ways of playing games. You can play just for fun with no thought of winning or losing. You may play recklessly, in the hope of lucking out and winning. You may play on the assumption that your opponent is foolish and attempt to exploit that foolishness. In a game of ticktacktoe with a child, you might even play to lose. This is all well and fine. It is not what game theory is about.
Game theory is about perfectly logical players interested only in winning. When you credit your opponent(s) with both rationality and a desire to win, and play so as to encourage the best outcome for yourself, then the game is open to the analysis of game theory.
Perfect rationality, like perfect anything, is a fiction. There’s no such thing as a perfectly straight line. This didn’t stop Euclid from developing a useful system of geometry. So it was with von Neumann and his perfectly rational players. You can think of the players of game theory as being something like the perfect logicians you hear about in logic puzzles, or even as being computer programs rather than human beings. The players are assumed to have perfect understanding of the rules and perfect memory of past moves. At all points in the game they are aware of all possible logical ramifications of their moves and their opponents’ moves.
This can be a stringent requirement. Perfectly rational players would never miss a jump in checkers or “fall into a trap” in chess. All legal sequences of moves are implicit in the rules of these games, and a perfectly logical player gives due consideration to every possibility.
But as anyone who plays chess or checkers knows, traps and missed moves—trying to get your opponent to fall for them, trying to recover when you fall for them—are pretty much what the games are all about. What would a game between two perfectly rational players be like?
You probably already know what happens when ticktacktoe is played “rationally.” It ends in a draw—it has to unless someone makes a mistake. Because ticktacktoe is so simple that it is possible to learn to play it perfectly, the game soon loses its appeal.
Von Neumann showed, however, that many other games are like ticktacktoe in this sense. Chess is not a game, von Neumann told Bronowski. He meant that there is a “correct” way(s) to play the game—although no one presently knows what it is—and that the game would therefore be trivial, in much the same sense as ticktacktoe, to players aware of the “correct” strategy.
The gist of von Neumann’s demonstration of this fact is marvelously simple. It applies not only to chess but to any game where no information is kept from the players, where “all the cards are on the table.”
Most familiar games take place as a sequence of moves by the players. In ticktacktoe, chess, or checkers, the grid or board is always visible to both players. No moves are taken in secret. For any such game, you can draw a diagram of all the possible courses of play. I’ll use ticktacktoe as an example because it’s fairly simple, but the same thing could be done, in principle, for chess, checkers, or any such game. Ticktacktoe starts with the first player (“X”) putting a mark in any of nine cells. There are consequently nine possible first moves. The nine choices open to Player X on the first move can be diagrammed as nine lines radiating up from a point. The point represents the move, the moment of decision, and the lines represent the possible choices.
Next it’s Player O’s move. There are eight cells still open—which eight depending on where the X is. So draw eight secondary branches at the top of each of the nine primary branches. That leaves seven open cells for X on his second move. As the diagram of possible moves is continued upward, it branches like a very bushy tree.
As you continue the process, you will eventually diagram moves that put three markers in a row. That’s a win for the player who moves. It’s also the termination of that particular branch in the diagram, for the game ends when someone gets three in a row. Mark that point (call it a “leaf” of the diagram) as a win for X or O as the case may be.
Other branches of the diagram will terminate in a tie. Mark them as ties. Obviously, the game of ticktacktoe cannot go on forever. Nine moves is the maximum. So eventually, you will have a complete diagram of the game of ticktacktoe. Every possible ticktacktoe game—every game that ever has been played or ever will be played—must appear in the diagram as a branch starting at the “root” (X’s first move) and continuing up to a “leaf” marked as a win for X, a win for O, or a tie. The longest complete branches/games are nine moves long. The shortest are five moves (this is the minimum for a win by the first player).
So much for the tree; now for the pruning shears. By process of elimination, you can figure out how to play ticktacktoe “rationally” from the diagram. The diagram contains all legal sequences of play, even those with stupid moves such as when someone overlooks a chance to get three in a row. All you have to do is take pruning shears to the tree and trim off all the stupid moves. What’s left will be the smart moves—the rational way to play.
A small portion of the diagram looks like this:

Go through the diagram and carefully backtrack from every leaf. Each leaf is someone’s last move, a move that creates a victory or a tie. For instance, at Point A, it is X’s move, and there is only one empty cell. X has no choice but to fill it in and create a tie.
Now look at Point B, a move earlier in the game. It is O’s turn, and he has two choices. Putting an O in one of the two open cells leads to the aforementioned Point A and a sure tie. Putting an O in the other cell, however, leads to a win for X. A rational O player prefers a tie to an X victory. Consequently, the right branch leading upward from Point B can never occur in rational play. Snip this branch from the diagram. Once the play gets to Point B, a tie is a foregone conclusion.
But look: X could have won earlier, at Point C. A rational X would have chosen an immediate win at Point C. So actually, we can snip off the entire left branch of the diagram.
Keep pruning the tree down to the root, and you will discover that ties are the only possible outcomes of rational play. (There is more than one rational way of playing, though.) The second player can and will veto any attempt at an X victory, and vice-versa.
What can be done for ticktacktoe could be done for almost any two-person game with no hidden information. The main restriction is that the game must be finite. It can’t go on forever, and the number of distinct choices at any move must also be finite. Otherwise, there are no “leaves” (last moves) to work back from.
Human beings being mortal, no recreational game is intended to go on forever. Rules of more challenging games rarely state a maximum number of moves explicitly, though. Chess normally ends in checkmate. There are many cases where pieces can be moved endlessly without creating a checkmate. Should captures reduce the board to just the two kings, neither will be able to checkmate the other. “Tie rules” bring such games to a halt. A common rule declares the game a tie when a sequence of moves repeats exactly three times. Another, more stringent, rule is that if no pawn is moved and no higher-ranking pieces are captured in forty moves, the game is a tie.
Consequently, von Neumann and Morgenstern pointed out, there is a numerical limit on the number of moves in a game of chess under a given tie rule. (The limiting number is probably around 5,000 moves with typical rules—far more than any game of chess ever played!) The actual value of the limit is not important to the proof, just that it exists and is finite. Given that a game of chess can run only so many moves, and that the number of choices at each move is finite, it follows that the number of different courses of play is itself a finite number. You could make a diagram of all legal courses of play, and prune it to reveal the rational way to play chess.
It recalls the old joke about the chess game where White makes his first move and then Black says, “I resign.” Chess between perfectly rational players would be as trivial as that. It is only because we do not know the correct strategy for chess that it still challenges players. It is one thing to prove that a best strategy exists, but it is quite another to do all the calculation and produce the strategy. It is unknown whether a rational game of chess would end in a victory (presumably for White, who moves first) or a tie.
There is another way of looking at games, one far more useful in game theory. A game is equivalent to a table of possible outcomes.
As we have shown, the number of possible games of chess is astronomically large but finite nevertheless. It follows that the number of chess strategies is finite, too. I have already used the word “strategy” several times; now is the time to define it. In game theory, strategy is an important idea, and it has a more precise meaning than it usually does. When chess players talk of a strategy, they mean something like “open with the king’s Indian Defense and play aggressively.” In game theory, a strategy is a much more specific plan. It is a complete description of a particular way to play a game, no matter what the other player(s) does and no matter how long the game lasts. A strategy must prescribe actions so thoroughly that you never have to make a decision in following it.
An example of a true strategy for first player in ticktacktoe would be:
Put X in the center square. O can respond two ways:
1 If O goes in a noncorner square, put X in a corner cell adjacent to the O. This gives you two-in-a-row. If O fails to block on the next move, make three-in-a-row for a win. If O blocks, put X in the empty corner cell that is not adjacent to the first (noncorner) O. This gives you two-in-a-row two ways. No matter what O does on the next move, you can make three-in-a-row after that and win.
2 If instead O’s first move is a corner cell, put X in one of the adjacent noncorner cells. This gives you two-in-a-row. If O fails to block on the next move, make three-in-a-row for a win. If O blocks, put X in the corner cell that is adjacent to the second O and on the same side of the grid as the first O. This gives you two-in-a-row. If O fails to block on the next move, make three-in-a-row for a win. If O blocks, put X in the empty cell adjacent to the third O. This gives you two-in-a-row. If O fails to block on the next move, make three-in-a-row for a win. If O blocks, fill in the remaining cell for a tie.
This shows how complicated a strategy can be, even for a very simple game. A true strategy for chess would be so huge that it could never be written down. There is not enough paper and ink on earth to list all the possibilities; there is not enough computer memory to loop through them all. This is one reason why computers still aren’t unbeatable at chess.
Overwhelming as this practical difficulty is, it didn’t bother von Neumann, and it needn’t bother us. In fact, since we’re fantasizing, we might as well go a step further. Not only could a perfectly rational being conceive of a strategy in full detail; he could—given no limits on memory or computing power whatsoever—anticipate every possible chess strategy and decide in advance what to do even before moving the first piece.
Suppose you had a numbered list of all possible strategies for chess. Then your choice of strategy is tantamount to selecting a number from 1 to n, where n is the (very, very large) number of possible strategies. Your opponent could choose a strategy from his list of possibilities (from 1 to m, say). Once these two strategies were chosen, the resulting game would be completely specified. By applying the two strategies you could move the pieces and bring the game to its preordained conclusion. Openings, captures, “surprise moves” and endgame would all be implicit in the choice of strategies.
To take this pipe dream to its conclusion, we can imagine that, given enough time, you could play out every possible pairing of strategies to see the outcome. The results could be tabulated in a rectangular table. The real table would span the galaxies, so we’ll print an abbreviated version here!

Once you had this table, you wouldn’t have to bother with the chessboard anymore. A “game” of chess would amount to the two players choosing their strategies simultaneously and looking up the result in the table.2 To find out who wins, you’d look in the cell at the intersection of the row corresponding to White’s strategy and the column of Black’s strategy. Should White choose to use strategy number 2 on his list, and Black choose to use his strategy number 3, the inevitable outcome would be a checkmate for White in 54 moves.
This isn’t the way real people play real games. To detail every possible contingency beforehand would be the antithesis of the word “play.” No matter. This idea of representing games as tables of outcomes turns out to be very useful. Every possible sequence of play for any two-person game can be represented as a cell in a similar type of table. The table must have as many rows as one player has strategies and a column for each of the other player’s strategies. A game reduced to a table like this is called the “normalized form” of the game.
The trick is deciding which strategy to choose. The table gets all the facts out in the open, but this isn’t always enough. The arrangement of outcomes in the table can be capricious. Neither player gets to choose the outcome he wants, only the row or column it appears in. The other player’s choice makes an equal contribution.
Look at the imaginary table for chess. Is strategy number 1 a good choice for White? It’s tough to say. If Black chooses strategy number 1, it’s good because that leads to a win for White. But with other choices for Black, the result can be a draw or a loss for White.
White really wants to determine which strategy Black is going to choose. Then all White has to do is make sure he picks one of his own strategies that will lead to a win when paired with the Black strategy.
Unfortunately, Black wants to do the same thing. Black wants to psych out White, and choose his strategy accordingly for a Black victory. Of course, White knows this, and tries to predict what Black will do based on what he thinks White will do …
Borel and von Neumann realized that this sort of deliberation puts games beyond the scope of probability theory. The players would be wrong indeed to assume that their opponent’s choice is determined by “chance.” Chance has nothing to do with it. The players can be expected to do their very best to deduce the other’s choice and prepare for it. A new theory is called for.
“Zero-sum game” is one of the few terms from game theory that has entered general parlance. It refers to a game where the total winnings or payoffs are fixed. The best example is a game like poker, where players put money in the pot, and someone wins it. No one ever wins a dollar but that someone else has lost it. It is in this restricted but quite diverse category of games that game theory has enjoyed its greatest success. The analogies to economics are obvious. One speaks of a “zero-sum society” meaning that one person’s gain is another’s loss: “There’s no such thing as a free lunch.”
Most recreational games are zero-sum. This is true even of games that don’t involve money. Whether money is at stake or not, each player prefers some possible outcomes to others. When these preferences are expressed on a numerical scale, they are called utility.
Think of utility as the “counters” in a game, or as “points” you try to win. If you play poker for matchsticks, and honestly try to win as many matchsticks as possible, then utility is identical with the quantity of matchsticks.
In a game played for money, money is utility or nearly so. When a game is played just to win, the mere fact of winning confers utility. In a win-or-lose game like ticktacktoe or chess, winning might be assigned a utility of 1 (in arbitrary “points”) and losing might be assigned a utility of −1 point. The sum of utilities is still zero, hence it is a zero-sum game.
An important thing to remember about utility is that it corresponds to the actual preferences of the players. In the case of an adult playing a child and wanting to lose, the adult’s utilities would be reversed: losing would have a utility of 1 and winning a utility of −1. Thus utility does not necessarily correspond to money, or winning or losing, or any obvious external object.
The simplest true game is a two-person, two-strategy, zero-sum game. The only way a game could be any simpler would be for a player to have just one strategy. But a “choice” of one option is no choice at all. The “game” would really be a one-person game, which is no game at all.
A two-person, two-strategy game can be diagrammed in a two-row by two-column table. If the game is further a zero-sum game, the outcomes can be represented concisely. Fill each of the four cells with a number representing the first player’s win. We know that the first player’s win is the second player’s loss, so both can use the same diagram (the second player’s wins are the negatives of the numbers in the table).
A two-person, zero-sum game is “total war.” One player can win only if the other loses. No cooperation is possible. Von Neumann settled on a simple and sensible plan for deciding rational solutions of such games. It is called the minimax principle.
Let’s reexamine the cake division problem from the perspective of game theory. The children are playing a zero-sum game. There is only so much cake to begin with, and nothing the children do will change the amount available. More cake for one means that much less cake for the other.
The first child (the “cutter”) has a range of strategies—strictly speaking, an unlimited number since he can cut the cake in any of an infinite number of ways. We will not miss much by simplifying the range of choices to just two strategies. One strategy is to split the cake unevenly and the other is to split the cake as evenly as possible.
The second child (the “chooser”) also has two strategies. He can choose the bigger piece or the smaller piece. (As a further note of realism, we’ll allow that no slicing operation is perfect. So even when the cutter adopts the policy of splitting the cake evenly, one piece will be slightly bigger than the other.)
A simple table illustrates the choices. We need put only one child’s payoff in the cells of the table. Let’s use the cutter’s payoff. Obviously, the chooser gets whatever is left. The table looks like this:
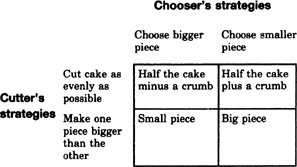
We already know what to expect of this game. The cutter will split the cake evenly, or try to as best he can. The chooser will pick the bigger piece. The result is the upper left cell. The cutter will get slightly less than half the cake, since the chooser will take the bigger of two nearly identical pieces.
Why this outcome? If the cutter could have his pick of any of the four possible outcomes, he would want to end up with a big piece (lower right cell). He realizes, however, that this is not realistic. The cutter knows what to expect from the chooser; namely, the worst—as small a piece as possible.
The cutter is empowered only to decide the row of the cake division’s outcome. He expects to end up with the least amount of cake in that row, for the chooser will act to minimize the cutter’s piece. Therefore he acts so as to maximize the minimum the chooser will leave him.
If the cutter cuts the cake evenly, he knows he will end up with nearly half the cake. If instead the cutter makes one piece much bigger, he knows as certainly that he will end up with a small piece. The real choice, then, is between nearly half the cake and much less than half. The cutter goes for nearly half the cake by electing to split the cake evenly. This amount, the maximum row minimum, is called the “maximin.”
“You know that the best you can expect is to avoid the worst,” writes Italo Calvino in If on a Winter’s Night a Traveler (1979). The epigram neatly states the minimax principle. The choice of strategies is a natural outcome. It is not merely a “fair” outcome recommended by game-theoretic arbitration but a true equilibrium enforced by both players’ self-interest. A player deviates from his best strategy to his own determent (and to his opponent’s benefit because it is a zero-sum game).
The minimax principle helps make sense of more difficult two-person zero-sum games. We have shown that almost any common game is logically equivalent to a simultaneous choice of strategies by players. Simultaneous games are thus different from cake division, where the chooser acts after the cutter has.
But look: What if the chooser had to go first by announcing his choice (bigger piece or smaller piece) before the cutter picked up the knife? It would make no difference at all. A rational chooser knows the cutter will divide the cake so that the chooser’s slice is as small as possible. The chooser in turn wants the cutter to get the smallest piece possible. (Remember, the table above gives the cutter’s piece, which is the complement of the chooser’s.) The chooser looks for the minimum column maximum (the “minimax”). It’s also the upper left cell. The chooser should go for the bigger piece.
In this game, the upper left cell is the natural outcome, regardless of which player is required to announce his strategy first. Consequently, we feel safe in saying that the upper left cell would be the logical result of a game where players had to decide simultaneously.
The value in the upper left cell is both the maximin (the cutter’s best “realistic” outcome) and the minimax (the chooser’s best realistic outcome, here expressed as what the cutter would get). You might wonder whether this is a coincidence, or whether it is always so. It is a coincidence, though not an unusual one in a small table. When the maximin and the minimax are identical, that outcome is called a “saddle point.” Von Neumann and Morgenstern likened it to the point in the middle of a saddle-shaped mountain pass—at once the maximum elevation reached by a traveler going through the pass and the minimum elevation encountered by a mountain goat traveling the crest of the range.
When a game has a saddle point, the saddle point is the solution of the game, the expected outcome of rational play. Note that a rational solution doesn’t necessarily mean that everyone is happy. The cutter ends up getting a crumb or two less than the chooser. He may not think that’s fair. For that matter, both players may be disappointed they didn’t get a much bigger piece. Neither player gets his first choice of outcome. What’s to prevent the players from striking out and doing something irrational?
The answer is greed and distrust. Half the cake minus a crumb is the most the cutter can guarantee for himself without any help from the chooser. It is also the smallest piece the chooser can leave for the cutter by his own efforts. To do any better, a player would need the assistance of his adversary. But the opponent has no reason to help—it’s less cake for him. The saddle-point solution of a zero-sum game is self-enforcing. It’s something like Chinese finger cuffs. The harder you struggle to do any better, the worse off you are.
Unfortunately, there’s a catch. Not all games have saddle points. The trouble is, you can invent a game with any rules you want. Any set of payoffs is conceivable. It is easy to fill a rectangular grid with numbers so that the minimum row maximum does not equal the maximum column minimum. Then there is no saddle point.
One of the simplest of all games has no saddle points. “Matching pennies” (which von Neumann and Morgenstern use as an example) is hardly a game at all in the usual sense. Two players simultaneously place a penny on a table—heads up or tails up. When the pennies match (both are heads or both are tails) the first player gets to keep both pennies. He gets back his own penny and wins his partner’s penny for a profit of 1 cent. If the pennies don’t match, the second player gets both.
The table for matching pennies looks like this:
| Heads | Tails | |
| Heads | 1 cent | −1 cent |
| Tails | −1 cent | 1 cent |
The minimum of both rows is −1 cent. Therefore the maximum minimum is also −1 cent. The maximum of both columns is 1 cent, so the minimum maximum is 1 cent too. There is a 2-cent difference between the minimax and the maximin.
Von Neumann and Morgenstern likened games to a “tug of war.” Each side can prevent the other from gaining too much ground, but there is a middle ground where the rope lurches back and forth. In matching pennies, the first player can guarantee himself his minimax value (−1 cent)—which isn’t saying much in this case, because that’s the maximum loss in the game. The second player is guaranteed that he can’t lose more than a penny. The difference between these two guarantees, 2 cents, is how much is really at stake in the game.
Should you choose heads or tails? Obviously, it all depends on what the other player will do. If you knew what the other player was going to do, you’d know what you want to do—and vice-versa.
As you probably know, the best way to play matching pennies is to play heads and tails randomly (with 50 percent probability each). This is called a “mixed strategy” in contrast to the “pure strategies” of playing heads with certainty or tails with certainty. Mixed strategies were nothing new in von Neumann’s time. Borel’s paper considered such strategies, and of course players of games like matching pennies have long appreciated the desirability of acting randomly. Sometimes matching pennies is used as a “random” way of deciding who gets an advantage in another game, such as which team bats first in baseball.
By fashioning a new, random strategy “from scratch,” the players create a self-enforcing equilibrium. Let’s make a new diagram for matching pennies that includes the random strategy.
| Heads | Tails | Random | |
| Heads | 1 cent | −1 cent | 0 |
| Tails | −1 cent | 1 cent | 0 |
| Random | 0 | 0 | 0 |
Anyone who plays randomly stands equal chances of winning and of losing a penny. (This is true whether the opponent plays a pure strategy or chooses randomly as well.) On the average, then, the payoff to a random player is 0. Fill in the row and column for the random strategies with 0’s.
Now there is a saddle point. If the first player had to name his strategy first (definitely heads, definitely tails, or a random choice), knowing that the second would take full advantage of that information, he’d want to choose the strategy with the maximum minimum. The strategies of heads or tails have minimums of −1 cent. The random strategy guarantees an average gain of 0, no matter what the other player does. Thus the random strategy has the maximum minimum.
If the second player had to go first, he would want the minimum maximum. Again this is the random strategy. Game theory suggests the lower right cell as the natural outcome. Both players should choose randomly. Once again we find an equilibrium between the players’ opposed interests.
Most five-year-olds already know how to play matching pennies. What do we need game theory for?
The answer is that other games are not quite so simple, and for them game theory can crank out impeccably correct prescriptions that are by no means common sense. The odds in a random strategy do not have to be fifty-fifty. They can and should be adjusted according to the payoffs. Game theory tells how to do this.
Here’s a nice little dilemma: “Millionaire Jackpot Matching Pennies.” It works just like ordinary matching pennies except that you play against fabulously wealthy opponents only, and if you match on heads, your opponent has to pay you a million dollars. Your payoffs are as follows (your opponent’s are just the opposite).
| Heads | Tails | |
| Heads | $1 million | −1 cent |
| Tails | −1 cent | 1 cent |
How should you play this game? Well, the pennies are chicken feed. You’re interested in winning that million dollars. The only way that can happen is for you to play heads. So your first impulse is to play heads.
But wait a minute, your opponent would be crazy to play heads. He’s not going to risk losing a million dollars. His first impulse is to play tails.
Should first impulses prevail, you’ll play heads and your opponent will play tails. There will be no match, and you will lose a penny to your opponent—hey, wasn’t this game supposed to be stacked in your favor?
At a deeper level of analysis, you realize that your opponent pretty well has to pick tails. Not only does that veto your big win (his big loss), but he collects a penny every time you pick heads and he picks tails.
Two can play at that game. As long as you know your opponent is virtually certain to pick tails, you can take advantage of that fact. Choose tails, and you’re almost sure to win a penny.
But maybe your opponent anticipates your double-cross. Then he might be tempted to play heads—or maybe not; he is risking a million that way. Still, if there’s any chance at all that he might play heads, maybe you should reconsider playing heads. You can well afford to give up winning a penny for a long shot at the million....
Game theory concludes that the correct mixed strategy is to play tails practically all the time. You should play heads with a probability of only about 2 in a 100 million (the exact ratio is 2:100,000,003.3 Your opponent should do the same thing.
The million-dollar payoff, which seems to be such a windfall, is mostly an illusion since the other player can veto it. Regular matching pennies is a fair game with zero expected value. The millionaire version is in your favor, but only in the amount of approximately one cent per play. That, of course, is what you win for matching tails. The net effect of the million-dollar payoff is to raise your average gain by one cent! It would not change your expectation of gain appreciably if the bonus were raised to a trillion dollars or a googol dollars.
The other surprising thing is the recommendation that the second player occasionally play the risky strategy of heads. He doesn’t play it much, but it is hard to rationalize playing it at all. Here’s one way of looking at it. The game is basically one of both players playing tails (lower right cell). But were the second player to foreswear playing heads completely, that would rule out any possibility of your winning the $1 million. You would have no reason ever to play heads either.
The second player (who almost always plays tails) likes it when you play heads. That action almost always results in a win for him. He has to play heads occasionally to give you some incentive to keep on playing heads every now and then. What’s more, these occasions when he plays heads usually turn out okay for him since you usually play tails.
Lightning rarely strikes twice. Provided both players play heads infrequently enough, the many, many cases of a single heads (and a penny’s gain for the second player) balance the infrequent catastrophe of both players playing heads. Thus there is an optimal mixed strategy where heads are played very infrequently but not avoided entirely.
Once you understand the idea of mixed strategies, you recognize them everywhere. Let’s give a few examples.
Baseball pitchers are better at throwing some types of pitches than others. All other things being equal, the batter would expect the pitcher to throw his best pitch all the time. But should the batter know the type of pitch to expect, he would gain an advantage. Pitchers therefore throw a random mixture of fast balls, slow balls, curve balls, and knuckle balls to keep the batter uncertain. The rare exception only proves the rule. When Satchel Paige was asked how he could get away with always throwing fast balls, he answered, “They know what’s comin’, but they don’t know where.”
In principle, game theory could prescribe the optimal mixture of pitches. The mixture would vary according to the relative strengths of each player’s pitches. You’d need some fairly exacting statistics—how many runs resulted from each type of pitch, ideally broken down by opposing batter. It would be interesting to see how closely pitchers’ instinctive strategies approximate that of game theory. The math is no more involved than that in some of the baseball statistics being kept, and this seems a natural project for a future Bill James.
As early as 1928, Oskar Morgenstern recognized a dilemma in Arthur Conan Doyle’s The Adventures of Sherlock Holmes. He and von Neumann cite it in their book:
Sherlock Holmes desires to proceed from London to Dover and hence to the Continent in order to escape from Professor Moriarty who pursues him. Having boarded the train he observes, as the train pulls out, the appearance of Professor Moriarty on the platform. Sherlock Holmes takes it for granted—and in this he is assumed to be fully justified—that his adversary, who has seen him, might secure a special train and overtake him. Sherlock Holmes is faced with the alternative of going to Dover or of leaving the train at Canterbury, the only intermediate station. His adversary—whose intelligence is assumed to be fully adequate to visualize these possibilities—has the same choice. Both opponents must choose the place of their detrainment in ignorance of the other’s corresponding decision. If, as a result of these measures, they should find themselves, in fine, on the same platform, Sherlock Holmes may with certainty expect to be killed by Moriarty. If Sherlock Holmes reaches Dover unharmed he can make good his escape.
Von Neumann and Morgenstern go so far as to assign points to the various outcomes and compute a mixed strategy. They recommend that Moriarty go to Dover with a 60 percent probability, and to Canterbury with a 40 percent probability. Holmes should get off at Canterbury (60 percent probability) or Dover (40 percent probability). The game is unfair, and Moriarty has a better chance of prevailing.
In Doyle’s story, Holmes gets out in Canterbury to see Moriarty’s special train passing on its way to Dover. It is interesting that both Holmes and Moriarty followed the most likely course under von Neumann and Morgenstern’s mixed strategy. They write, “It is, however, somewhat misleading that this procedure leads to Sherlock Holmes’ complete victory, whereas, as we saw above, the odds (i.e. the value of a play) are definitely in favor of Moriarty.... Our result … yields that Sherlock Holmes is as good as 48% dead when his train pulls out from Victoria Station.”
This kind of calculated deception resembles bluffing in poker. Poker can be quite complex, in part because it usually has more than two players. Von Neumann analyzed a simplified form of poker. In outline, his conclusions apply to the real game. He showed that you should always bid aggressively when you have a strong hand. With a weak hand, you should sometimes bluff (bid aggressively anyway).
Von Neumann distinguished two reasons for bluffing. A player who never bluffs misses many chances to call the other player’s bluffs. Suppose that both you and your opponent have bad hands. You don’t bluff; your opponent does. That means you fold and your opponent wins without a showdown. Had you also bluffed, your lousy hand would have been compared with his lousy hand, and you might have won. The bluffer can exploit the nonbluffer; ergo, von Neumann’s rational player must bluff.
Bluffing is also a smoke screen. As in matching pennies, one wants to keep the other player guessing. Poker hands are dealt randomly to begin with, but players form opinions about their opponent’s hands from their bids. Judicious bluffing prevents a player from being too predictable.
Game theory has important analogies in biology. A person who inherits the relatively rare sickle-cell anemia gene from one parent has greater immunity to malaria, but someone who inherits the gene from both parents develops sickle-cell anemia, a deadly disease. The puzzling survival of this and other lethal genes probably involves an equilibrium much like that in a bonus-payout version of matching pennies.
In the latter game, a player picks the risky strategy of heads at rare intervals in order to get a benefit that accrues when just that player plays heads. The sickle-cell gene is likewise risky but confers a benefit when only one gene is present. Provided the gene is rare enough in the population, cases of the disease are rare compared to cases of enhanced immunity. This is believed to be the reason this seemingly unfavorable gene has persisted in areas where malaria is common.
You might wonder how this has anything to do with game theory. Genes can’t choose mixed strategies or any kind of strategies. As it turns out, conscious choice is not essential to game theory. At the most abstract level, game theory is about tables with numbers in them—numbers that entities are efficiently acting to maximize or minimize. It makes no difference whether you picture the entities as poker players who want to win as much money as possible or as genes mindlessly reproducing as much as natural selection permits. We’ll hear more about biological interpretations of game theory later.
The minimax theorem proves that every finite, two-person, zero-sum game has a rational solution in the form of a pure or mixed strategy. Von Neumann’s position as founder of game theory rests mainly with his proof of the minimax theorem by 1926. Von Neumann considered the theorem crucial. In 1953 he wrote, “As far as I can see, there could be no theory of games on these bases without that theorem.... Throughout the period in question I thought there was nothing worth publishing until the ‘minimax theorem’ was proved.”
To put it in plain language, the minimax theorem says that there is always a rational solution to a precisely defined conflict between two people whose interests are completely opposite. It is a rational solution in that both parties can convince themselves that they cannot expect to do any better, given the nature of the conflict.
Game theory’s prescriptions are conservative ones. They are the best a rational player can expect when playing against another rational player. They do not guarantee the best outcome possible. Usually a rational player can do better for himself when playing an irrational opponent. Sometimes these benefits accrue even to the rational player sticking with the prescribed strategy. In other situations it is necessary for the rational player to deviate from the strategy of game theory to take advantage of the other player’s irrationality. An example is matching pennies. Say that you’re the matching player and are mixing heads and tails equally and randomly. But you notice that your less rational opponent is unconsciously choosing “heads” more than half the time. Then you can come out ahead by choosing “heads” more often.
Sensible as this modification is, the modified strategy is no longer the optimal one and opens you to possible exploitation yourself (such as by a third player, or by the irrational opponent should he suddenly “wise up.”)
A journalist once asked von Neumann if game theory would help make a killing in the stock market. Honestly enough, von Neumann answered no. Such questions lingered. What is game theory good for? If not to play games, then what?
Von Neumann himself saw the minimax theorem as the first cornerstone of an exact science of economics. Toward this end, much of von Neumann and Morgenstern’s book treats games with three or more persons. Most of the time, the number of “players” in an economic problem is large—huge even—and no simplifying assumptions are possible.
A game with an arbitrary number of players is called an “n-person game.” A complete analysis of such games is much more complex than zero-sum two-person games. Conflicts of interest are less pat. What is good for player A may be bad for player B but good for player C. In such a situation, A and C might form an alliance. Such coalitions change a game radically.
In a three-person game, it is possible that two players acting in concert can guarantee a win. Two allies might thus cut a third player out of his share of winnings. Von Neumann and Morgenstern tried to decide when such coalitions were likely to form, and who was likely to form them. Would weak players gang up against a strong player? Or would weak players try to ally themselves with a strong player? One conclusion was that many potential coalitions can be stable. Then it is difficult or impossible to predict what will happen.
Von Neumann hoped to use the minimax theorem to tackle games of ever more players. The minimax theorem gives a rational solution to any two-person zero-sum game. A three-person game can be dissected into sub-games between the potential coalitions. If players A and B team up against player C, then the resulting game (coalition of A and B vs. C) is effectively a two-person game with a solution guaranteed by the minimax theorem. By figuring out the results of all the potential coalitions, the players A, B, and C would be able to decide which coalitions were most in their interests. This would then give a rational solution to a three-person game.
There’s no need to stop there. A four-person game can be chopped up into two- and three-person games between its potential coalitions. Hash out all the possibilities there, and the solution will be evident. Four-person games lead to five-person games, six-person games, ad infinitum.
Unfortunately, the complexity of games, and of the necessary computations, increases exponentially with the number of players. If the economy of the world can be modeled as a 5-billion-player “game,” that fact may be of little practical use. In the main, von Neumann and Morgenstern’s work on economics never got off the ground. It remains for someone else to extend their foundations.
Good mathematician that he was, von Neumann did not try to limit his theory to its nominal subject matter. Geometry arose out of problems of surveying land. Today we find nothing unusual about using geometry in contexts that have nothing to do with real estate. A rectangle is a rectangle whether it’s someone’s farm or an abstract rectangle in a geometric proof. Von Neumann and Morgenstern point out that a zero-sum n-person game is in effect a function of n variables, or alternatively, an n-dimensional matrix. Much of the discussion in Theory of Games and Economic Behavior applies to such abstract functions or matrices irrespective of whether they are pictured as payoff tables for games, outcomes of economic or military decisions, or anything else. Game theory is inspired by, but not necessarily about, games.
Real conflicts postponed further development of game theory. Like many of his colleagues, von Neumann enlisted in the war effort. This left little time for pure research. Von Neumann would never again publish ground-breaking work in pure mathematics at the heady clip of the years between the world wars. Paul Halmos wrote (1973), “The year 1940 was just about the half-way point of von Neumann’s scientific life, and his publications show a discontinuous break then. Till then he was a topflight pure mathematician who understood physics; after that he was an applied mathematician who remembered his pure work.”
1. Retention of immature traits in adulthood. Bronowski alludes to the fact that non-human animals play and experiment in their youth, then lock into a successful pattern of behavior (compare the playful kitten with the contented old cat).
2. Why “simultaneously”? Doesn’t Black at least get to see White’s first move before deciding on his strategy? No: you’re failing to appreciate how comprehensive a strategy must be. The first part of a Black strategy would prescribe a Black opening move for each of the twenty possible opening moves by White. Not until each of these twenty contingencies is accounted for do you have a strategy in von Neumann’s sense.
3. I’m not getting into the actual math here because it’s not needed to understand social dilemmas. For “generalized matching pennies”—a two-person, zero-sum game with two strategies for each player—the correct mixed strategy is easy to calculate. Write the payoffs in a two by two grid as usual. Then calculate the differences of the two payoffs in each row and write them to the right of the table:
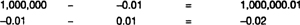
Make both results positive (−0.02 becomes 0.02) and swap them:
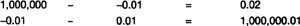
This means the proper odds for heads:tails is 0.02:1,000,000.01, or (multiplying by 100 to get rid of the decimals) 2:100,000,001. The other player calculates his odds by figuring the differences in the columns and swapping. In this case the odds are the same for both players. It’s more complicated for games with more than two strategies. If you’re interested, see John Williams’s The Compleat Strategyst.