For the modeling process, we will follow the following steps:
- Extract the components and determine the number to retain
- Rotate the retained components
- Interpret the rotated solution
- Create the factor scores
- Use the scores as input variables for regression analysis
There are many different ways and packages to conduct PCA in R, including what seems to be the most commonly used prcomp() and princomp() functions in base R. However, for my money, it seems that the psych package is the most flexible with the best options. For rotation with this package, you will also need to load GPArotation.
To extract the components with the psych package, you will use the principal() function. The syntax will include the data (pca.df) and number of the components to extract. We will try 5, and we will state that we do not want to rotate the components at this time. You can choose not to specify nfactors, but the output would be rather lengthy as it would produce k-1 components:
> pca = principal(pca.df, nfactors=5, rotate="none")
We will examine the components by calling the pca object that we created, as follows:
> pca Principal Components Analysis Call: principal(r = pca.df, nfactors = 5, rotate = "none") Standardized loadings (pattern matrix) based upon correlation matrix PC1 PC2 PC3 PC4 PC5 h2 u2 gg 0.83 0.05 -0.10 0.45 0.04 0.90 0.10 gag -0.82 0.04 -0.01 0.35 0.31 0.89 0.11 five 0.90 -0.11 -0.15 -0.02 -0.20 0.89 0.11 PPP 0.16 0.76 0.30 0.34 -0.20 0.86 0.14 PKP 0.70 -0.20 0.12 -0.44 -0.08 0.75 0.25 shots 0.61 0.35 -0.43 -0.04 0.38 0.81 0.19 sag -0.63 -0.42 0.33 0.12 0.45 0.90 0.10 sc1 0.82 -0.11 0.36 -0.06 0.02 0.81 0.19 tr1 0.74 -0.14 -0.40 0.31 0.08 0.83 0.17 lead1 0.82 0.04 0.40 0.15 0.06 0.86 0.14 lead2 0.75 -0.10 0.42 -0.04 0.25 0.81 0.19 wop 0.71 -0.20 -0.24 -0.16 0.24 0.68 0.32 wosp 0.84 -0.24 0.07 0.27 -0.03 0.84 0.16 face 0.28 0.74 0.06 -0.36 0.31 0.86 0.14 PC1 PC2 PC3 PC4 PC5 SS loadings 7.19 1.63 1.13 1.00 0.75 Proportion Var 0.51 0.12 0.08 0.07 0.05 Cumulative Var 0.51 0.63 0.71 0.78 0.84 Proportion Explained 0.61 0.14 0.10 0.09 0.06 Cumulative Proportion 0.61 0.75 0.85 0.94 1.00
At first glance, this looks quite a bit to digest. First of all, let's disregard the h2 and u2 columns. We will come back to h2 after the rotation. There are two important things to digest here in the output. The first is the variable loadings for each of the five components that are labeled PC1 through PC5. We see with component one that almost all the variables have high loadings except for the power play percentage, PPP, and the faceoff win percentage, face. These two variables have high loading values on component two. Component three is quite a hodgepodge of the mid-value loadings. The highest two variables are tr1 and PKP. Component four seems rather odd and difficult for us to pull out a meaningful construct. So, we will move on to the second part to examine: the table starting with the sum of square, SS loadings. Here, the numbers are the eigenvalues for each component. When they are normalized, you will end up with the Proportion Explained row, which as you may have guessed, stands for the proportion of the variance explained by each component. You can see that component one explains just over half (61 percentage) of all the variance explained by the five components.
There are a number of ways in which we can select our final set of components. We could simply select all the components with an eigenvalue greater than one. In this case, we would keep the first four. We could use the proportion of total variance accounted for, which in the preceding table is the cumulative var row. A good rule of thumb is to select the components that account for at least 70 percent of the total variance, which means that the variance explained by each of the selected components accounts for 70 percent of the variance explained by all the components. In this case, three or four components would work. Perhaps, the best thing to do is apply judgment in conjunction with the other criteria. With this in mind, I would recommend going with just three components. It captures 71 percent of the total variance in the data and from my hockey fanatic point of view, is easier to interpret.
Another visual technique is to do a scree plot. A scree plot can aid you in assessing the components that explain the most variance in the data. It shows the Component number on the x axis and their associated Eigenvalues on the y axis. Therefore, I will present to you the much used scree plot as follows. We want to plot the associated eigenvalues from the pca object.
> plot(pca$values, type="b", ylab="Eigenvalues", xlab="Component")
The following is the output of the preceding command:

What you are looking in a scree plot is similar to what I described previously about the eigenvalues that are greater than one and the point where the additional variance explained by a component does not differ greatly from one component to the next. In other words, it is the break point where the plot flattens out. In this, three components look pretty compelling.
As we discussed previously, the point behind rotation is to maximize the loadings of the variables on a specific component, which helps in simplifying the interpretation by reducing/eliminating the correlation among these components. The method to conduct orthogonal rotation is known as "varimax". There are other non-orthogonal rotation methods that allow correlation across factors/components. The choice of the rotation methodology that you will use in your profession should be based on the pertinent literature, which exceeds the scope of this chapter. Feel free to experiment with this dataset. I think that when in doubt, the starting point for any PCA should be orthogonal rotation.
For this process, we will simply turn back to the principal() function, slightly changing the syntax to account for just 3 components and orthogonal rotation, as follows:
> pca.rotate = principal(pca.df, nfactors=3, rotate = "varimax") > pca.rotate Principal Components Analysis Call: principal(r = pca.df, nfactors = 3, rotate = "varimax") Standardized loadings (pattern matrix) based upon correlation matrix PC1 PC3 PC2 h2 u2 com gg 0.57 0.59 0.15 0.69 0.31 2.1 gag -0.65 -0.49 -0.09 0.67 0.33 1.9 five 0.64 0.66 -0.01 0.85 0.15 2.0 PPP 0.09 -0.05 0.83 0.70 0.30 1.0 PKP 0.66 0.32 -0.06 0.55 0.45 1.5 shots 0.13 0.75 0.31 0.67 0.33 1.4 sag -0.18 -0.70 -0.41 0.68 0.32 1.8 sc1 0.87 0.21 0.11 0.81 0.19 1.2 tr1 0.38 0.75 -0.12 0.73 0.27 1.5 lead1 0.85 0.19 0.26 0.83 0.17 1.3 lead2 0.84 0.13 0.13 0.75 0.25 1.1 wop 0.46 0.60 -0.15 0.60 0.40 2.0 wosp 0.76 0.44 -0.08 0.77 0.23 1.6 face 0.05 0.21 0.77 0.63 0.37 1.2 PC1 PC3 PC2 SS loadings 4.78 3.44 1.72 Proportion Var 0.34 0.25 0.12 Cumulative Var 0.34 0.59 0.71 Proportion Explained 0.48 0.35 0.17 Cumulative Proportion 0.48 0.83 1.00 Mean item complexity = 1.5 Test of the hypothesis that 3 components are sufficient. The root mean square of the residuals (RMSR) is 0.08 with the empirical chi square 34.83 with prob < 0.97 Fit based upon off diagonal values = 0.97
You can see that the rotation has changed the loadings, but the cumulative variance has not changed. We can now really construct some meaning around the components.
If you examine PC1, you will see the high negative correlation with the goals allowed per game in conjunction with a high rate of killing penalties and a high win rate if scoring first. Additionally, this component captures the high loadings with winning after having a lead at the end of the first or second period. The 5-on-5 ratio and winning when outshot are the frosting on the cake here. What I think we have in this component is the essence of defensive hockey including the killing penalties. The teams with high factor scores on this component would appear to be able to get a lead on an opponent and then shut them down to gain a win.
PC3 appears to simply be a good offense. We will see a high loading for the goals scored per game, 5-on-5 scoring ratio, and shots per game. Additionally, look at how high the loading is for the winning after trailing at the end of the first period variable.
I think that PC2 is the easiest to identify. It is the high loading value for the power play success and winning faceoffs. When we did the correlation analysis during the data exploration, we saw that these two variables were moderately correlated with each other. Any hockey fan can tell you how important it is for a team on the power play to win the faceoff, control the puck, and run their set plays. This analysis seems to show that these two variables do indeed go hand in hand.
We will now need to capture the rotated component loadings as the factor scores for each individual team. These scores indicate how each observation (in our case, the NHL team) relates to a rotated component. Let's do this and capture the scores in a data frame as we will need to use it for our regression analysis:
> pca.scores = pca.rotate$scores > pca.scores = as.data.frame(pca.scores) > pca.scores PC1 PC3 PC2 1 -1.33961165 -2.07275625 -2.38781073 2 -1.83244527 -1.12058364 0.77749711 3 -0.31094630 -1.62938873 -0.44133187 4 -1.02855311 -0.15704421 1.37199872 5 -2.68517373 -0.13231693 -0.27385509 6 -0.20853619 0.01524553 -0.46863716 7 0.10587046 -1.62940123 -0.42949901 8 -0.01324802 0.14959828 0.68875225 9 0.38541531 -0.59307204 -1.08937869 10 -0.15009774 -0.86256283 1.53513596 11 0.84099339 0.25043743 -0.52846404 12 0.24423775 0.36681320 -0.08995115 13 -0.68188634 1.09817128 0.53636881 14 1.18243869 0.34770042 0.35777454 15 -0.34720957 0.73064512 -0.53796910 16 -0.27227305 -0.09055833 1.34309546 17 -0.46350916 1.76830702 -0.94260357 18 1.06460458 0.24810967 -0.42634091 19 0.68720947 -1.39593941 0.35981827 20 0.72661065 0.31415750 -0.32705332 21 0.05533420 0.33660090 1.34849134 22 -0.23245895 0.77728066 -1.22841259 23 0.80098114 0.20634248 -0.93200321 24 1.22510788 -1.05511121 1.96984298 25 1.07648218 -0.54999695 -0.47064277 26 0.40911681 0.97327087 1.29704632 27 -1.53540552 2.44287010 -0.29119483 28 1.65378121 0.40998320 -1.20495883 29 -0.47171243 0.26403013 0.67952937 30 1.11488330 0.58916795 -0.19524429
We now have the scores for each factor for each team. These are simply the variables for each observation multiplied by the loadings and summed. Remember that we ordered the observations by total points from the worst to the best. As such, you can see that a team such as BUFFALO in the first row has negative factor scores across the board.
Before we begin the regression analysis, let's prepare the NHL data frame. The two major tasks are to convert the total points to numeric and attach the factor scores as new variables. We can accomplish this with the following code:
nhl$pts = as.numeric(nhl$pts) nhl$Def = pca.scores$PC1 nhl$Off = pca.scores$PC3 nhl$PPlay = pca.scores$PC2
With this done, we will now move on to the predictive model.
To do this part of the process, we will repeat the steps and code from Chapter 2, Linear Regression – The Blocking and Tackling of Machine Learning. If you haven't done so, please look at Chapter 2, Linear Regression – The Blocking and Tackling of Machine Learning for some insight on how to interpret the following output.
We will use the following lm() function to create our linear model with all the 3 factors as inputs and then summarize the results:
> nhl.lm = lm(pts~Def+Off+PPlay, data=nhl) > summary(nhl.lm) Call: lm(formula = pts ~ Def + Off + PPlay, data = nhl) Residuals: Min 1Q Median 3Q Max -8.7891 -1.3948 0.5619 2.0406 6.6021 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 92.2000 0.7699 119.754 < 2e-16 *** Def 11.2957 0.7831 14.425 6.41e-14 *** Off 10.4439 0.7831 13.337 3.90e-13 *** PPlay 0.6177 0.7831 0.789 0.437 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 4.217 on 26 degrees of freedom Multiple R-squared: 0.937,Adjusted R-squared: 0.9297 F-statistic: 128.9 on 3 and 26 DF, p-value: 1.004e-15
The good news is that our overall model is highly significant statistically, with p-value of 1.004e-15 and Adjusted R-squared is over 92 percent. The bad news is the power play factor is not with p-value of 0.437. We could simply choose to keep it in our model, but let's see what happens if we exclude it:
> nhl.lm2 = lm(pts~Def+Off, data=nhl) > summary(nhl.lm2) Call: lm(formula = pts ~ Def + Off, data = nhl) Residuals: Min 1Q Median 3Q Max -8.3786 -2.0258 0.7259 2.4748 6.3295 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 92.2000 0.7645 120.60 < 2e-16 *** Def 11.2957 0.7776 14.53 2.79e-14 *** Off 10.4439 0.7776 13.43 1.81e-13 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 4.187 on 27 degrees of freedom Multiple R-squared: 0.9355,Adjusted R-squared: 0.9307 F-statistic: 195.7 on 2 and 27 DF, p-value: < 2.2e-16
This model still achieves a high Adjusted R-squared value (93.07 percent) with statistically significant factor coefficients. I will spare you the details of running the diagnostic tests. Instead, let's look at some plots in order to examine our analysis better. We can do a scatterplot of the predicted and actual values (the total team points) with the base R graphics, as follows:
> plot(nhl.lm2$fitted.values, nhl$pts, main="Predicted versus Actual",xlab="Predicted",ylab="Actual")
The following is the output of the preceding command:

This confirms that our model does a good job of using two factors to predict the team's success and also highlights the strong linear relationship between the principal components and team points. Let's kick it up a notch by doing a scatterplot using the ggplot2 package and include the team names in it. We will also focus only on the upper half of the team's point performance. We will first create a data frame of the 15 best teams in terms of points and call it nhl.best. Let's also include the predictions in the nhl data frame and sort it with the points in a descending order:
> nhl$pred = nhl.lm2$fitted.values > nhl=nhl[order(-nhl$pts),] > nhl.best = nhl[1:15,]
The next endeavor is to build our scatterplot using the ggplot() function. The only problem is that it is a very powerful function with many options. There are numerous online resources to help you navigate the ggplot() maze, but this code should help you on your way. Let's first create our baseline plot and assign it to an object called p, as follows:
> p = ggplot(nhl.best, aes(x=pred, y= pts, label=team))
The syntax to create p is very simple. We just specified the data frame and put in aes() what we want our x and y to be along with the variable that we want to use as labels. We now just add layers of neat stuff such as data points. Add whatever you want to the plot by including + in the syntax, as follows:
> p + geom_point() +
Then, we will specify how we want our team labels to appear. This takes quite a bit of trial and error to get the font size and position in order:
geom_text(size=3.5, hjust=.2, vjust=-0.5, angle=15) +
Now, specify the x and y axis limits, otherwise the plot will cut out any observations that fall outside them, as follows:
xlim(90,120) + ylim(90, 120) +
Finally, add a best fit line with no standard error shading and you get the following plot:
stat_smooth(method="lm", se=FALSE)
The following is the output of the preceding command:
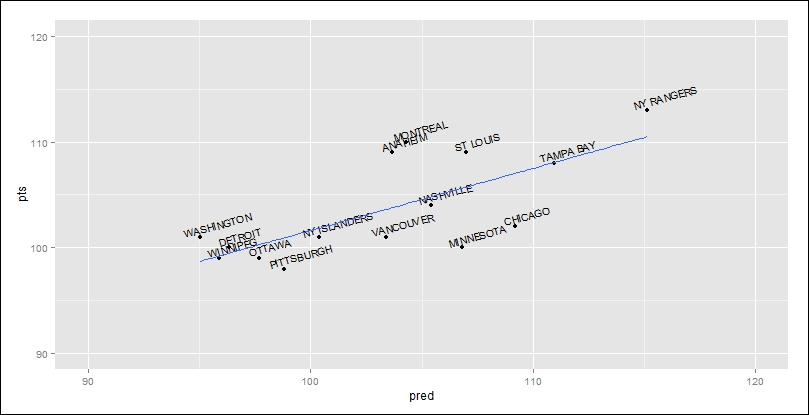
I guess one way to think about this plot is that the teams below the line underachieved, while those above it, overachieved. For instance, the MINNESOTA Wild had a predicted point total of 102 but only achieved 95. At any rate, this is overly simplistic but is fun to ponder nonetheless.
The final bit of analysis will be to plot the teams in relationship to their factor scores. Once again, ggplot() facilitates this analysis. Using the preceding code as our guide, let's update it and see what the result is:
> p2 = ggplot(nhl, aes(x=Def, y=Off, label=team)) > p2 + geom_point() + geom_text(size=3, hjust=.2, vjust=-0.5, angle=0) + xlim(-3,3) + ylim(-3,3)
The output of the preceding command is as follows:
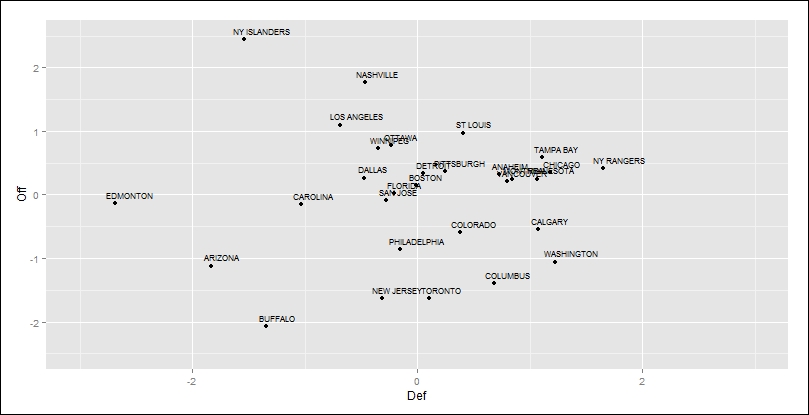
As you can see, the x axis is the defensive factor scores and the y axis is the offensive factor scores. Look at the NY ISLANDERS with the highest offensive factor scores but one of the worst defensive scores. I predict an early exit in the upcoming playoffs for them, considering the old adage that offense puts people in the seats but defense wins championships. Indeed, here is a link to an excellent article discussing the Islander's struggles and their poor ratio of winning when leading after the second period at http://www.cbssports.com/nhl/eye-on-hockey/25134251/how-concerned-should-the-islanders-be-heading-into-the-playoffs. Do the most balanced teams such as the NY RANGERS, TAMPA BAY, and others have the best chance to win a title? We shall see!
When I first wrote this chapter, the NHL playoffs were just starting. It was probably the best race for Lord Stanley's Cup that I have seen. Many of my fellow fans agree with this assertion. As predicted, the Islanders were out after the first round after a brutal series with the Washington Capitals as their defense lived up to its reputation, or lack thereof. The big surprise was how the Blackhawks refused to lose and ended up winning it all. Like a boxer with a puncher's chance, they got off the canvas and threw some well-timed haymakers. Note that I am a longtime Blackhawks fan going back to the days of Troy Murry and Eddie Belfour (all former Fighting Sioux). It was good for Jonathan Toews to win another title, especially after being robbed by the refs in the 2007 NCAA Frozen Four semifinal with T.J. Oshie as his linemate. However, I digress.