4.2. When silly mistakes may not be that silly
What I used to think
I used to think that students who made silly mistakes were lazy and careless. A missing unit of measurement here, an incomplete final step there, and before you knew it crucial exam marks were disappearing down the drain. Silly mistakes were the bane of my life. My technique for stopping my students making such mistakes? Repeatedly tell them not to be so careless, of course.
Strangely, this did not seem to work.
Sources of inspiration
- Sweller, J., Van Merriënboer, J. J. G. and Paas, F. G. W. C. (1998) ‘Cognitive architecture and instructional design’, Educational Psychology Review 10 (3) pp. 251-296.
My takeaway
Consider the following question:
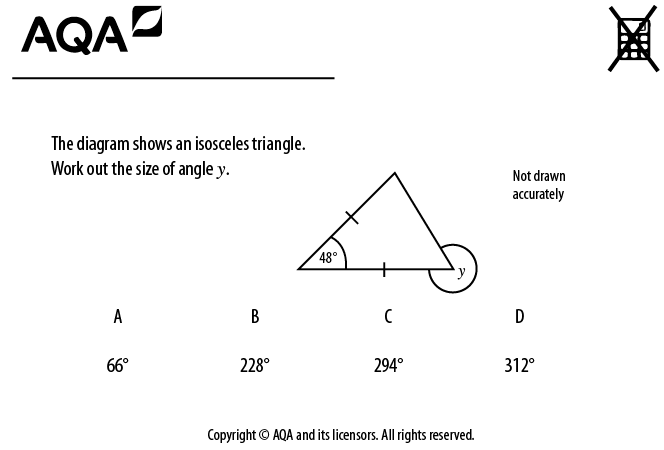
Figure 4.1 – Source: AQA for Diagnostic Questions
At the time of writing, this question has been answered well over 10,000 times on my Diagnostic Questions website.
Now, it may come as little surprise to you that the most popular incorrect answer is D (chosen by 22% of respondents), with students who are used to the conventional orientation of an isosceles triangle assuming that the bottom-right angle is also equal to 48°. However, would it surprise you that 18% of students answering this question went for A?
How on earth could anyone believe that the answer to this question was 66°? What a silly mistake!
Or is it?
Having considered Cognitive Load Theory and the workings of memory, I am not so sure any more. We can shed some light onto students’ thought processes by reading some of the explanations they gave to accompany their choice of A on my Diagnostic Questions website:
180 take away 48 is 132, and 132 divided by 2 is 66, meaning both the sides are 66°.
I think that the answer is 66 because with isosceles triangles the two bottom angles are the same. So I turned the screen to find that the side two angles look closely identical, so I then took 48 from 180 because I knew that angles in a triangle add to 180, so then I got the answer 132, then I divided that by two, to get 66.
Both really nice pieces of thinking, but notice that the final step – namely subtracting their answer from 360 – is missing each time. Now this could be a silly mistake, but it could also be the result of cognitive overload.
Consider what a student might need to process in their working memories to solve this problem:
- What is the question asking?
- What do the angles in a triangle add up to?
- What type of triangle is it?
- How does that help me?
- Which are the base angles?
- What is 180 – 48?
- What is 132 ÷ 2?
Now, if the student’s working memory is full to the brim by the time they reach the end of this chain of thinking, then ‘What is the question asking?’ may well have been bumped out, or there may simply be no spare cognitive capacity to process 360 – 66. In other words – and this is my technical term – they are cognitively knackered. In such a scenario, it is not surprising that the student settles upon an answer of 66°.
We can see here how domain-specific expertise, and the associated way of thinking that accompanies it, can help this process. For an expert, this question has a relatively low intrinsic load. They are likely to immediately recognise this as an isosceles triangle problem – indeed, they may have solved an unconventional one like this in the past – and will easily be able to retrieve the answers to the calculations with little burden placed upon working memory. Hence, they have capacity left to complete the problem, check it makes sense, and also assimilate it into their long-term memories and hence learn from the process.
Here are a selection of other ‘silly mistakes’ that may indeed be the result of cognitive overload. In each case, notice how it is the final stage of the process where the mistake occurs – in other words at the very point when working memory is likely to be feeling the greatest strain.
- Doing a simultaneous equations problem and ‘forgetting’ to find y
- Estimating the mean from a grouped frequency table and ‘forgetting’ to divide by total frequency
- Completing an area problem and ‘forgetting’ to put the units in
- Doing a tree diagram question and ‘forgetting’ to add the fractions together at the end
- Solving a quadratic equation using the formula and ‘forgetting’ to round the answers to one decimal place
- Adding two fractions together and ‘forgetting’ to simplify the answer
What I do now
When a student makes what I would have previously dismissed as a ‘silly mistake’, I now ask myself if carelessness really is the cause, or could it be cognitive overload? If it is the latter, then telling the student to be more careful next time is likely to be a fruitless exercise. Instead, I need to equip them with the knowledge they need to successfully solve such problems, and ensure as much of it as possible is automated.
But this is a long-term solution, making use of the principles of explicit instruction together with the practical strategies described in the chapters that follow. However, there are more immediate steps we can take to reduce extraneous load, and hence increase the chances of our students solving problems like this successfully.