7.2. Examples v Rules
What I used to think
Okay, so we have established that definitions and explanations may be difficult to understand, but surely nothing beats a clear, unambiguous rule for carrying out a procedure? After all, aren’t such rules the foundations upon which maths is built?
Hence, I would happily present rules to my students, attempt to show where these rules came from, get them to neatly copy the rule down in their books, and give students plenty of practice of them.
What could possibly go wrong?
Sources of inspiration
- Anderson, J. R. (1996) ‘ACT: a simple theory of complex cognition’, American Psychologist 51 (4) pp. 355-365.
- Morgan, J. (2017) ‘Topics in Depth’, Resourceaholic maths blog. Available at: http://www.resourceaholic.com/2017/06/topics.html.
- Pearce, J. (2016) ‘Reflections on #MathsConf5 – The dangers of students over- or under-generalising’, Must-be Maths blog. Available at: http://www.mustbemaths.com/2015/09/reflections-on-mathsconf5-dangers-of.html
- Skemp, R. R. (1976) ‘Relational understanding and instrumental understanding’, Mathematics Teaching 77 (1) pp. 20-26.
- Sweller, J., Van Merriënboer, J. J. G. and Paas, F. G. W. C. (1998) ‘Cognitive architecture and instructional design’, Educational Psychology Review 10 (3) pp. 251-296.
My takeaway
Let’s consider five common rules in mathematics:
- To find the mean you add up all the numbers and divide by however many numbers there are.
- Angles on a straight line add up to 180°.
- Two minuses make a plus.
- To expand a bracket, multiply everything on the outside by everything on the inside.
- When you multiply two indices with the same base, you add the powers.
These rules each have the advantage that they are short, written in relatively easy to understand language, and not too tricky to remember. The problem is, time and time again students misapply them due to problems of over- and under-generalisation.
Let’s briefly look at each rule in turn.
To find the mean you add up all the numbers and divide by however many numbers there are
This rule is ideal if you do indeed have a list of numbers. But what happens when students encounter mean from a frequency table? Or estimating the mean from grouped data? Or working backwards from the mean to find a given value? All of a sudden our rule appears rather deficient and something else is needed. In the words of James Pearce, we have ‘over-generalised’.
A common response is to argue that when students first encounter the mean it is usually only in the context of a list of numbers, and so that definition works fine. However, we return to Section 1.5 where we looked at building methods that last. What happens in Years 8 and 9? If students learn one rule for the mean for a list of numbers, then another for a frequency table, another for grouped frequency, another for backwards means, and so on, then all of a sudden we have several concepts, each of which is potentially viewed as separate from the others, all prone to being misremembered or misapplied.
Angles on a straight line add up to 180°
This rule looks safe enough. But consider the following question below from my Diagnostic Questions website:
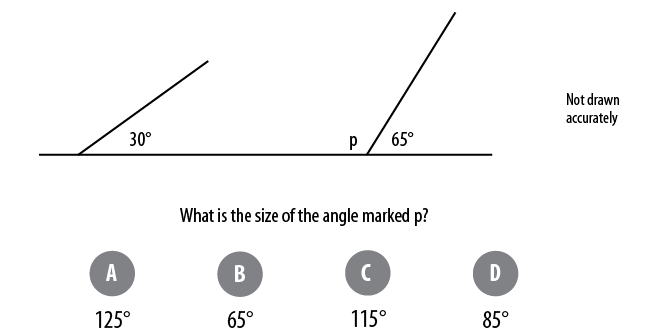
Figure 7.4 – Source: Craig Barton, created for Diagnostic Questions
If I told you that 35% of students at the time of writing opted for D) 85°, we can once again see the dangers of over-generalisation as all angles on the straight line are considered.
Two minuses make a plus
This is arguably the most dangerous rule in mathematics, prone to over-generalisation and misapplication by students of all ages. A student with this mantra echoing in their heads will inevitably stumble when faced with -7 – 5.
To expand a bracket, multiply everything on the outside by everything on the inside
This rule sounds perfectly safe, until, that is, you consider something like: 2 + 3(4x – 1). I certainly do not want everything on the outside being multiplied by everything on the inside. Once more, the perils of over-generalisation are plain to see.
When you multiply two indices with the same base, you add the powers
This rule can lead to a nasty case of under-generalisation. If students only ever encounter this rule in the context of positive bases and powers that are integers, such as 83 × 86, then the rule implicitly becomes when you multiply two indices with the same positive base, you add the integers in the powers together. Hence, there is a danger that when faced with any of the following, students may come unstuck, fearing they need another rule to help them answer the questions:
(–2)3 × (–2)6
71.4 × 70.3
3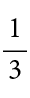 × 3
× 3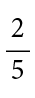
(x + y)3 × (x + y)-6
1.82n × 1.83n
The problem is that it is virtually impossible to write each of these rules in a way that covers all the possible twists and turns that students could encounter, avoiding the traps with over- and under-generalisation. Try it with the rule for finding the mean to see how tricky it is. ‘To find the mean you add up all the numbers, but if these numbers are in a frequency table then you need to multiply the frequency by the number to get the partial sum, oh and if the frequency table is grouped then you first need to get an unbiased estimate for the numbers by finding the midpoint…’. Doesn’t exactly roll off the tongue.
Indeed, in the context of arguing for Relational Understanding over Instrumental Understanding, Skemp (1976) points out that ‘if the teacher asks a question that does not quite fit the rule, of course they will get it wrong’. But for me, that is not an argument against instrumental understanding – I discuss the argument further in Section 3.9 – it is an argument for ensuring we give students examples such that they may develop a deeper understanding of the concept before the presentation of any rule.
From the models of thinking we looked at in Chapter 1, in particular those proposed by Anderson and Sweller, we can infer that it is better to focus on the ideas behind a concept rather than an algorithm for solving a particular subset of cases. Algorithms that only work in a few cases are less compatible with the development of the connected body of knowledge that form the long-term memories of experts. Likewise, continually having to decide which algorithm is suitable for a given case is likely to impose a significant burden upon working memory and threaten cognitive overload. Hence, we may surmise that it is good practice for students to encounter different types of cases as soon as possible in learning about a concept, to avoid incorrect over- and under-generalisations being embedded, which can be very difficult to resolve.
It is worth repeating that students do not learn from what we say and do; they learn from their own individual interpretations of what we say and do. Hence, as we saw with definitions and explanations above, presenting the examples and non-examples first should lead to a deeper understanding of a concept than a rule which may be applied either too narrowly or too broadly.
What I do now
Rules may be misunderstood or misapplied by students, leading to nasty cases of over- and under-generalisation. Well-chosen and well-presented examples and non-examples can illustrate a rule better than words ever can. They can help students arrive at a place where they already have a sound understanding of the rule before it is crystallised into words. Indeed, with enough good examples, followed by the Intelligent Practice we will look at later in this chapter, students may never need to rely on remembering an abstract rule at all.
Consider the rule: angles on a straight line add to 180°. To help address and hopefully rectify some of the misconceptions associated with this rule, students could again be presented with a selection of scenarios and asked to identify when this rule can be applied. Jo Morgan put together the following collection as part of her excellent ‘Topic in Depth’ series, where the question posed is, ‘Which pairs of angles will sum to 180°?’:

Figure 7.5 – Source: Jo Morgan, available at http://www.resourceaholic.com/2017/06/topics.htm
Finally, a quick word on negative numbers, for I feel this is a topic I have routinely failed to teach well for about ten years. I started with the two minuses make a plus rule, and then – as discussed in Section 3.7 – ‘progressed’ onto a dodgy analogy involving soup. Neither was successful.
Now I introduce negative numbers via sequences of carefully chosen examples, utilising humans’ natural tendency to spot patterns discussed in Section 3.4. So, a sequence of examples to develop the ability to subtract negative numbers may look like this:
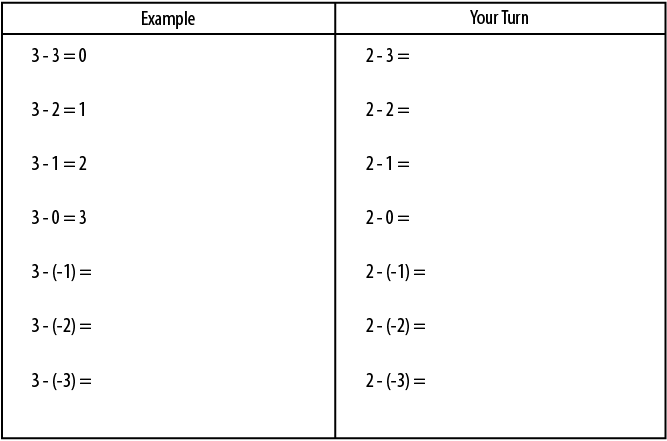
Figure 7.6 – Source: Craig Barton
Next I would present a sequence that begins with a negative number, and I would do similar sequences for each of the operations.
I present these examples in silence, pausing briefly before writing each answer down, making little fuss, and then give my students similar patterns to complete themselves on mini whiteboards. Crucially, I then ensure students receive regular practice of isolated questions (ie not presented in a pattern) at spaced intervals throughout the coming weeks, months and year. These will appear in the homeworks and low-stakes quizzes that will be discussed in Chapter 12. This way, students develop fluency for dealing with negative numbers, which is far superior to a rule prone to misapplication, or a dubious analogy.
All of this is not to say that rules – just like definitions – do not have a place. Rules can clarify, summarise and be committed to memory. Just like definitions, rules also remove the need for an infinite number of examples and non-examples to understand a concept. However, rules that are not first preceded by well-chosen and well-presented examples and non-examples can often lead to trouble.