1.1. A simple model of thinking and learning

What I used to think

The next 15 words I am about to write are more than a little worrying: in 12 years of teaching, I never really considered how my students think and learn. A teacher not considering how their students think and learn is kind of like a doctor not being overly concerned about the workings of the body, or a baker taking only a casual interest in the best conditions for bread to rise. If we don’t know how students think and learn, how on earth can we know how to teach them effectively?

I had vague notions of concepts like working memory and schema, but vague is certainly the operative word. So, I went about my business, blissfully unaware of my own ignorance, going off nothing more than intuition to try to teach students to the best of my abilities.

Sources of inspiration

My takeaway

As thinking and learning are clearly such important parts of teaching, they are also going to be crucial parts of this book. With that in mind, it is important early on to establish a model of how students think and learn. Any attempt to reduce something as complex as human cognition to a model that can be explained in a couple of pages is fraught with danger. But as Dylan Wiliam explains in a 2017 article for TES: ‘what makes a model valuable is not how accurate it is – any model can be made more accurate by making it more complex – but rather the trade-off between simplicity and power. This is particularly important when we look at the human brain, which is probably the most complex thing in the universe’.

Fortunately, there are sufficient commonalities across leading research to enable us to form a basic model for how thinking and learning occurs that will serve us well for what follows.

How students think

For Willigham (2009), thought occurs when you combine information in new ways, and successful thinking relies on four factors: information from the environment, facts in long-term memory, procedures in long-term memory, and space in working memory. If any one of these factors is deficient, thinking will likely fail.

Let’s take a closer look at those two components of memory.

Long-term memory

For Mccrea (2017), long-term memory may be thought of as our mental model of the world: a map we construct ourselves, holding facts, procedures, beliefs, mindsets and dispositions. Long-term memory represents what we know and who we are and informs how we act. It has no known limits. All of the information stored in long-term memory resides outside of awareness, lying there patiently until it is needed, before entering working memory and becoming conscious.

Throughout this book, the facts and procedures stored in long-term memory will be grouped together under the term knowledge. When I say I want my students to have a good knowledge of fractions, I mean I want them to know relevant facts, such as what a numerator is and that three-quarters is more than one-quarter, as well as to be able to carry out relevant procedures, such as how to add, simplify and divide fractions. I also want as much of this knowledge as possible to be automated, so students know instantly that a half of 24 is 12 and that to add fractions you need a common denominator, without imposing any strain on their working memories. Later on in this book there will be the need to be more specific with the nature of this knowledge, in particular when we come to consider procedural fluency and conceptual understanding in Section 3.9 and the eternal question about teaching the How before the Why. But for now, think of knowledge as the interconnected facts and procedures stored and organised in long-term memory that allow us humans to operate.

This knowledge is stored and organised in long-term memory in schemas (see Piaget, 1928; Bartlett, 1932; and Anderson, 1977). Schemas do this by incorporating or chunking multiple elements of related information into a single element with a specific function. So, you may have a schema for adding fractions, which contains all the relevant knowledge you have acquired over many years. There is no limit to how complex schemas can become, or how many can be stored in long-term memory. Indeed, for the proponents of Cognitive Load Theory (eg Sweller et al, 1998) to prevent cognitive overload, the ability to solve problems demands the acquisition of tens of thousands of these domain-specific schemas, together with the automation of key knowledge following extensive practice. Therefore, long-term memory is not just a vast databank of knowledge, but an integral component of all cognitive activity.

According to Anderson’s (2012) Adaptive Character of Thought (ACT-R) theory, complex cognition arises from an interaction of declarative and procedural knowledge. Declarative knowledge is factual knowledge that can be reported or described, and its most basic unit is a chunk. Procedural knowledge is dynamic and involves rules, or productions, that guide how thinking occurs. Declarative knowledge can be acquired quickly from direct encoding of the environment, while procedural knowledge takes longer and must be compiled from declarative knowledge through practice. After a certain amount of practice, the path of production becomes stable and procedural learning has occurred.

It is worth noting that psychologists and maths teachers are likely to have different interpretations of the term procedure. Psychologists mainly think in terms of procedures derived from implicit memories, such as tying a shoelace or driving a car. Whilst maths contains examples of such procedures – experts fluently adding fractions or rearranging equations, for example – there are also procedures that rely on more explicit memories, such as working through a multi-step trigonometry question slowly and methodically. But the key point remains the same – the conditions under which we learn procedures are determined by existing declarative knowledge.

There are two key implications from Anderson’s model that we will revisit many times throughout this book:

  1. Existing knowledge makes thinking and learning easier.
  2. Once something has been learned – whether it is correct or not – it is very difficult to unlearn. Hence, practice does not make perfect, practice makes permanent.

Working memory

Working memory is best viewed as the place where thought occurs. It is all about the here and now. Unlike long-term memory, working memory has a finite capacity, with Cowan (2010) estimating the number of items that can be held and processed at any one time to be around four. Cognitive Load Theory (eg Sweller et al, 1998; and Chapter 4 of this book) is primarily concerned with the limits of working memory. The theory is centred around the way in which a learner’s cognitive resources are focused and used during problem-solving, suggesting that for instruction to be effective, care must be taken to not overload the mind’s capacity for processing information. If working memory experiences cognitive overload, no learning may take place. We can get around working memory’s restrictive limit by chunking related information, carefully designing instruction and automating key knowledge.

Putting these related approaches together, we are able to form a very simplified model of how students think. This will be constantly revisited and expanded upon throughout this book, but the fundamentals will remain the same. The model looks like this:

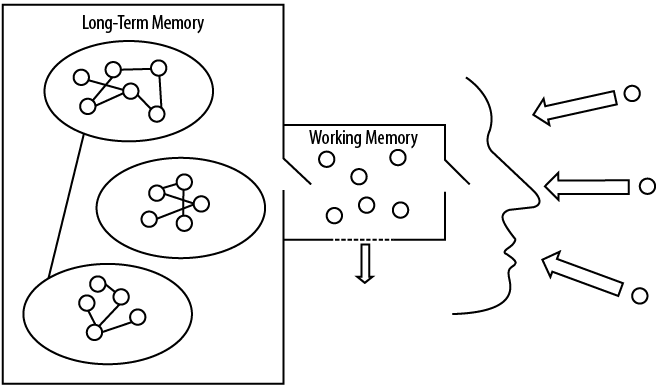
Figure 1.1 – Source: Craig Barton

The circles represent units of knowledge, the ovals are schemas, and the lines represent connections. Thinking takes place in working memory, focused on the interplay between the environment and what we retrieve from long-term memory. The more knowledge we have stored and organised in long-term memory, and the more of this knowledge that is automated, the easier thinking is and the more we can think about. Knowledge helps students take in more information, think about new information, and remember new information.

This simple model has huge implications for teaching and learning that we will delve into in the remainder of this chapter and throughout this book.

How students learn

There are many different definitions about what learning is, but the one I am going to opt for throughout this book is provided by Kirschner, Sweller and Clark (1998), who define learning as ‘a change in long-term memory’, going on to say that if nothing has changed in long-term memory, then nothing has been learned. Working memory is the vehicle that instigates this change.

It is worth noting that not everyone agrees with this definition. In a 2017 blog post, Daniel Willingham points out that this definition does not specify that the change in long-term memory must be long-lasting (so does that mean that a change lasting a few hours qualifies?), nor does it specify that the change must lead to positive consequences (does a change in long-term memory that results from Alzheimer’s disease qualify as learning?). In Chapter 12 we will address the first point – the durability of learning, and how we can improve it. The second point is beyond the scope of this book, but in Section 3.8 we will consider the acquisition of incorrect knowledge, and the difficulties of resolving it.

Our definition of learning implies that knowledge in long-term memory is not static. We acquire brand new knowledge, we adapt, change or accommodate existing knowledge based upon new experiences and information, and knowledge may become more or less accessible. This is all summed up beautifully by Mccrea (2017) who explains that knowledge ‘is constantly evolving and decaying as a result of our thinking and interaction with the environment. Our long-term memory is more like a forest than a library’.

For Coe (2013), learning happens when people have to think hard, and indeed making changes to long-term memory is likely to be effortful. There are two main pathways through which such a change may occur, and – in a sense – they travel in opposite directions to each other:

From working memory to long-term memory

Students learn new ideas by reference to ideas they already know. A learner holds information in working memory, and then makes connections between that information and knowledge already stored in long-term memory (assuming such knowledge is present). For Willingham (2009), ‘understanding is remembering in disguise’ – it is taking correct old ideas from long-term memory, getting them into working memory, and rearranging them in a new order to make new connections. So, if a student encounters algebraic fractions for the first time, they will (hopefully) make connections between their existing organised knowledge of non-algebraic fractions, rules of algebra, factors and so on. If they are unable to do this – either due to cognitive overload or because such knowledge does not exist in their long-term memory – then learning is unlikely to take place. However, if new ideas, information, facts and procedures are successfully processed in working memory, they may become assimilated into an existing schema or create a brand-new connected one, thus changing long-term memory.

From long-term memory to working memory

When information is successfully retrieved from long-term memory into working memory, its representation in long-term memory is changed such that it becomes more accessible in the future. Using our memories changes our memories – or as Bjork (1975) put it, ‘retrieval is a powerful memory modifier’. Thus, the act of retrieval can result in learning. This rather surprising pathway to learning will be the focus of Chapter 12, and I promise it is worth waiting for.

What I do now

I think a lot about…well, thinking. Specifically, how can I design my teaching to ensure:

  1. …my students are thinking about the right things?
  2. …what they think about is transferred to long-term memory?
  3. …once it is in long-term memory, it can be accessed?
  4. …it can be applied successfully to different situations?

I will try my very best to answer these questions in this book.