8.2. The five stages of Deliberate Practice
What I used to think
As I have already confessed, I used to think the best way to introduce a complex process was to do it as a whole.
This time, let’s take a process such as adding two fractions together. My examples would probably look something like this:



I would emphasise the need to find a suitable common denominator, then look at the process of transforming the fractions so that the two denominators were the same, before finally explaining how we finish off the problem. My students would successfully answer my cue-laden prompts and questions, before embarking upon plenty of practice to ensure they too could carry out this process in one go, just like me.
Some students would inevitably struggle. But, I reasoned, that was probably because they had not been listening properly.
Sources of inspiration
- Barton, C. (2017) ‘Kris Boulton – Part 1’, Mr Barton Maths Podcast.
- Boulton, K. (2017) ‘My best planning – Part 2’, To the real maths blog. Available at: https://tothereal.wordpress.com/2017/08/19/my-best-planning-part-2/
- Ericsson, K. A., Krampe, R. T. and Tesch-Römer, C. (1993) ‘The role of Deliberate Practice in the acquisition of expert performance’, Psychological Review 100 (3) pp. 363-406.
- Ericsson, K. A. and Pool, R. (2016) Peak: secrets from the new science of expertise. Boston, MA: Houghton Mifflin Harcourt.
- Ericsson, K. A., Prietula, M. J. and Cokely, E. T. (2007) ‘The making of an expert’, Harvard Business Review 85 (7/8) pp. 114-121.
- Hin-Tai Ting (2017) ‘Is this the best we can do? Part 7: the spacing effect’, Mathagogy Blog. Available at: https://mathagogy.wordpress.com/2017/07/29/the-best-we-can-do-7-the-spacing-effect/
My takeaway
In the last section I discussed the need to break down a complex process into sub-processes for novice learners. Failure to do so means it is incredibly difficult to isolate the exact nature of difficulties students encounter, and tackling the process as a whole could lead to cognitive overload with no learning taking place. Now we will look at what we do next. Inspired by the work of Ericsson and others, I call this The Five Stages of Deliberate Practice:
- Isolate the skill.
- Develop the skill.
- Assess the skill.
- The final performance
- Practise retrieval later.
Let’s see this in operation when introducing how to add fractions.
1. Isolate the skill
As we saw in the previous section, we need to circumvent the curse of knowledge and think really carefully about the sub-processes involved. For example, the process of adding two fractions together could be broken down as follows:
- Decide if the fractions are in a form ready to be added.
- Decide on an appropriate common denominator.
- Use knowledge of equivalent fractions to transform the fractions.
- Complete the addition.
- Simplify the answer.
2. Develop the skill
In order to develop these individual skills, we need to use the lessons learned from Chapters 6 and 7, specifically example-problem pairs, examples and non-examples, and Intelligent Practice.
So, for ‘decide if the fractions are in a form ready to be added’, I may start by writing up pairs of fractions on the board, one at a time, indicating in silence which ones are in a form to be added in the manner I described when introducing the concept of an equation in Section 7.1. Alternatively, I may look to develop conceptual understanding using diagrams of shapes split up into fractions to illustrate that it is the denominator that determines if the fractions are in the correct form.
I would then present students with the following set of questions:
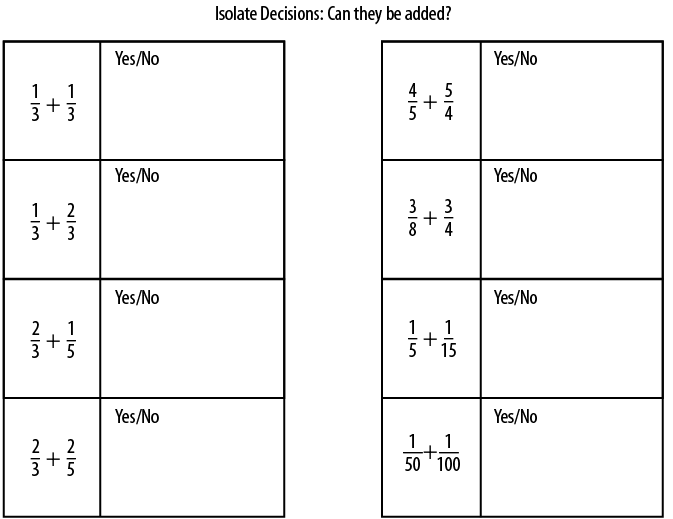
Figure 8.1 – Source: Craig Barton
This is a simple yes/no activity. I would get students to complete it on mini whiteboards and it should take them no more than a minute. It has been designed to ensure that students know to focus upon the denominator and not the numerator, and avoid any traps concerning multiples. If the activity does take more than a minute, then it is probably because a misconception has been identified that needs addressing – and I would much rather address it here instead of trying to unpick it whilst wrapped up in the more complex process of adding fractions.
Similarly, when developing ‘decide on an appropriate common denominator’, I would complete an example-problem pair and then give my students something like:
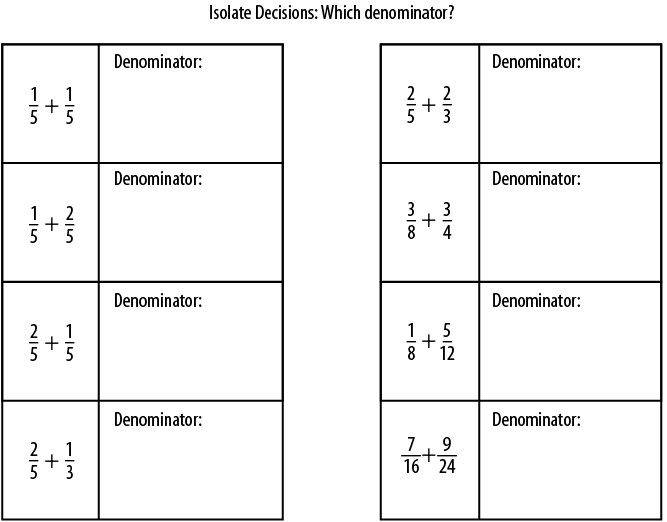
Figure 8.2 – Source: Craig Barton
As discussed in Chapter 7, my aim is for a logical variation and progression through the questions, so students can focus on what has changed and what has stayed the same, and the subsequent impact upon their answers. Notice that the ability to successfully complete this activity requires students to understand and be able to find lowest common multiples. This would have been assessed at the start of the lesson as required baseline knowledge in the manner that will be discussed in Chapter 11, and reinforced during the example-problem pair.
3. Assess the skill
Assessment of the skill does not need to immediately follow the development stage. In fact, given the distinction between learning and performance that we will cover in Chapter 12, this may not be the optimal time to assess. Instead, I may do it at the end of the lesson or the start of the next.
My preferred forms of assessment are low-stakes quizzes (Chapter 12) or diagnostic multiple-choice questions (Chapter 11). An example of the latter for the sub-process ‘decide on an appropriate common denominator’ might be:

Figure 8.3 – Source: Craig Barton, created for Diagnostic Questions
We will cover the rationale and the different ways of using these types of questions in Chapter 11, but it is worth noting here that my aims are to identify any misconceptions and their specific nature, and to see if I have enough evidence to move on.
4. The final performance
Once all sub-processes have been isolated, developed and assessed, it is time for the final performance. I would use the Supercharged Worked Example approach (Chapter 6) to ensure that students had an opportunity to observe me model the entire process and self-explain at key points. Then it would be time to practise. This may simply consist of a question or series of questions that bring all the sub-processes together. In this case, a selection of standard questions on adding fractions is perfect. Exam questions are also fine to use, but it is worth noting that contextual questions can place an extra burden upon students’ fragile working memories that I may wish to avoid at this stage of the learning process. Despite the intensive process students have been through to get to this stage, they are still novice learners, and I would be inclined to keep context out until they have mastered the entire process of adding fractions.
5. Practise retrieval later
The importance of inducing the retrieval of knowledge over different time intervals will be discussed in Chapter 12, but it is important here to note that successful performance at the assessment stage may not be a reliable indication of learning. It is necessary to practise retrieval again at some points in the future when students have had an opportunity to start to forget. As we will see, this serves the dual function of making any assessment aimed at discerning understanding more reliable, as well as improving the storage strength of that knowledge in long-term memory.
This retrieval practice may come in the form of inclusion of a question on a low-stakes quiz, homework, or as part of a mixed-topic starter. It may consist of the final performance (in this case a pair of fractions to add), or any one of the sub-processes that have been identified.
A note about timing
When I interviewed Kris Boulton for my podcast, he described how he planned to cover the series of 13 sub-processes that he identified to master solving simultaneous equations over a sequence of lessons. For example, he may cover Sub-process 1 in the first lesson, then recap it by means of a test of retention in the second, before moving on to Sub-process 2. These two sub-processes would then be assessed in the same lesson where Sub-process 3 was developed, and so on, ensuring that all sub-processes are routinely revisited. Kris describes this sequence in more detail in a follow-up blog post, which can be found in the Sources of inspiration.
However, there is nothing to say that these individual skills and sub-processes need to be taught one after another. The very fact that they have been isolated means they can be tackled independently from each other and the process as a whole. Indeed, there may be a very good argument for separating them over time. We will discuss the power of the Spacing and Interleaving Effects far more in Chapter 12, but for now it is worth reflecting on a 2017 blog post by Hin-Tai Ting, a maths teacher at Michaela Community School. Hin-Tai describes his department’s use of the Connecting Math Concepts curriculum, which is a direct instruction programme designed in consultation with Siegfried Engelmann. Here, a 60-minute lesson will consist of at least 8 different parts, with multiple concepts being covered. Indeed, the blog post showcases one particular part of a lesson that simply tests whether pupils remember the locations of the quotient, divisor and dividend – separate from any actual division – before moving on to unrelated questions concerning written addition and place value. The process of written division will be subsequently developed over many lessons, alongside the revisiting of all the other skills students have been taught.
What I do now
I follow the five stages of Deliberate Practice when I am introducing a complex process. And as I have become more experienced doing this, I have come to the realisation that if I am defining complex processes as anything with multiple steps in it, then that is pretty much the whole of the mathematics I teach. Things that are single processes for me are not for my students. For example, before we go anywhere near any calculations, working out the area of a triangle needs to start by identifying what shapes are (and are not) triangles, and what lengths represent (and do not represent) the ‘base’ and ‘perpendicular height’.
But by isolating, developing, assessing, performing and practising retrieval later, I can help students transition along the path to expertise so that they begin to see these as single processes like I do.