10.2. What is Purposeful Practice?

What I used to think

I used to think there were two types of activities you could give students: practice and problems to solve. Practice, as I have argued throughout this book, was necessary in the early knowledge acquisition phase of learning. Problem-solving came later, when students had reached a certain level of domain-specific expertise, and would help push their understanding of concepts to the next level. I did not think there was anything in between these two extremes.

Fortunately, I was wrong.

Sources of inspiration

My takeaway

Given the different experiences students have had with many of the topics they encounter in mathematics that I outlined in the previous section, there is a need for another type of activity. Teacher-guided instruction is ideal for novices, less-guided approaches are more beneficial for experts, but in most classes we have a mixture of the two, along with everything else in between. As such, we need something that gives the students sufficient practice to develop knowledge and procedural fluency, whilst at the same time providing opportunities to develop conceptual understanding and the problem-solving attributes discussed in Chapter 9 that experts possess.

The name I will give to the special type of activities or tasks that enable this is Purposeful Practice.

Let me show you what I mean with an example.

Say I am teaching my Year 9 class and I want to review their ability to add fractions. Maybe this is the first lesson in a Fractions Review unit, or maybe I taught them how to add fractions yesterday and now I want to give them more practice. I would start with an initial assessment of understanding, making use of diagnostic questions as discussed in Chapter 11. This may identify some major misconceptions that need dealing with there and then. Or it might reveal that some students simply need a reminder of the basic procedure, which can be achieved efficiently by means of Chapter 6’s example-problem pairs. But what do we do next?

Sure, I could give my students a series of fractions to add. But even if I carefully sequenced the questions using the principles of Section 7.8’s Intelligent Practice, they are still questions, presented in the same format as they always have been. And for the reasons outlined in the section above, this is unlikely to be suitable for many of my students.

So instead, I could give them the following:

Figure 10.1 – Source: Colin Foster for NRCIH, available at https://nrich.maths.org/13205

This problem gives students plenty of practice of the key skill of adding fractions, but with a wider purpose. How close can the students get to 1? How have they approached this? How do they know if they are closer to 1 than their friend? Is there a quicker way to do this? And then if some students settle upon an answer, we can push them further – what if they could only use 3 fractions? How about 4? What if they can subtract fractions as well? Can they create a set of fractions that will allow them to get to 1 in multiple ways? Students end up adding more fractions than they ever would if they were presented on a worksheet and in a way that rarely causes a moan, and they have the opportunity to develop wider skills along the way. This is an example of Purposeful Practice.

Purposeful Practice – at least in the way I define the phrase – is based around five key principles:

1. Students need to experience early success

In Chapter 2, I argued that too much struggle and failure can be a bad thing for learning, and furthermore that achievement and students’ perception that they can succeed are key drivers of motivation. Hence, any task or activity needs to give students the sense that they are making progress, or that they can make progress, pretty early on. This is the problem with many open-ended, unstructured tasks – the barrier to entry is just too high.

2. There must be plenty of opportunities to practise the key procedure

We have seen in the chapters on examples and Deliberate Practice just how important practice is. Whether students are responding to example-problem pairs or working through a carefully planned sequence of questions, it is the practice at their own pace and the opportunities to self-explain that helps knowledge transfer from working memory to long-term memory which is necessary for learning to take place. And we need them practising a specific procedure. One of the oft-cited strengths of unstructured, open-ended tasks is that students can tackle them lots of different ways. But I do not always want that. If I am revising a certain procedure or concept, then I want to make sure that students are practising the thing I intend.

3. The practice should feel different

Students have met many of these concepts and topics before. Presenting them again with another worksheet of boring questions, or even another Tarsia jigsaw to cut up, is likely to be demoralising. The student who did not understand it first time around is unlikely to believe that things will be any different this time. Likewise, the student who did understand it is likely to question why on earth they are being asked to do the same thing again.

4. Opportunities must exist for students to make connections, solve problems and think deeper

Success in maths is not just about answering routine questions. Students need to be able to transfer their knowledge to novel situations, spot connections, solve complex problems and think creatively. Indeed, once students reach a certain level of expertise, the sorts of activities that enable them to do this are the very ones that are needed to push their understanding on to the next level.

5. The focus is always on the practice

But there is no fast track to expertise. Students have to develop inflexible knowledge first. They have to have knowledge stored, available and automated in long-term memory in order to free up the cognitive capacity needed to make these connections, solve these problems, and crucially to learn from the experience. And it is worth pointing out again that students must be practising the thing I intend. Sure, they can make connections, solve problems and think deeper, but carrying out the intended procedure must always be at the forefront of the task.

Purposeful Practice is powerful because:

There is no need to create a different set of worksheets for all the perceived different abilities of students in your class. There are no big, potentially dangerous decisions to be made as to when to move students on to the next task. Differentiation is done by time and the connections students make.

Because the practice feels different, and because there is a larger goal in mind, students are more prone to engage in the sort of practice that is crucial in order to develop the knowledge and procedural fluency they need in order to master the topic.

Driskell et al (1992) along with Rohrer and Taylor (2006) suggest that over-learning – or learning beyond the point of mastery – can be beneficial. This is related to the distinction between learning and performance that we will consider in the next few chapters, but the key point is that learning can still improve after performance has seemingly peaked. Hence, even experts are likely to benefit from the sort of practice of key skills involved in Purposeful Practice activities.

The point of these tasks is that the practice has a wider purpose. There is a connection to spot, a relationship to explain, a shortcut to discover, a challenge to be solved, a surprise to rationalise. All of these things cause students to pause and consider what they are doing far more than if they were simply working their way through a series of unconnected questions on autopilot. This is linked to our work on Intelligent Practice in Chapter 7. By working through the calculations, pupils develop procedural fluency, but also have the opportunity to develop wider conceptual understanding. If they are secure in their own knowledge, they may also be able to share their thoughts and help others.

This is the key to it all. Throughout this book we have focused on the difference between novices and experts. Novice learners benefit from teacher guidance and routine practice, whereas the Expertise-Reversal Effect suggests that experts may not. Conversely, expert learners benefit from independent problem-solving activities, whereas Cognitive Load Theory suggests that novices may not. Everyone benefits from Purposeful Practice, both experts and novices and the large contingent of students who are making the journey between the two.

Whilst developing my own ideas for Purposeful Practice, I came across the fantastic work of Colin Foster and his ‘mathematical études’, which we discussed in depth when I interviewed him for my podcast. The key to an étude – a term of musical origin – is that a self-imposed constraint brings out creativity. In an article for NRICH, Foster (2017a) explains:

These are intended to be not just lovely rich tasks, but lovely rich tasks that force students’ attention onto a particular, important mathematical procedure. So etudes don’t allow students a choice of method. Allowing students to choose what method they use is often a great idea, but if you want them to develop their skill at a specific technique, then you have to force them to use that technique, otherwise they can end up unwittingly avoiding their areas of weakness by (perhaps cleverly) solving the problem some other way than you intended. So, mathematical etudes are designed with a specific procedure in mind. But, rather than simply asking students to perform that procedure repeatedly (as with tedious exercises), in an etude there is some wider problem-solving goal – something a bit more interesting is going on at the same time!

The answers obtained to the procedure matter for some wider purpose, and so students are more likely to carry out the procedure carefully and check what they have done. Wrong answers are more likely to be challenged by a peer if they matter for some wider purpose. And having something else to focus on beyond the procedure should help to promote the desired automaticity of carrying it out.

Foster (2017b) presents evidence that mathematical études are comparable to traditional exercises in their effects on procedural fluency, going on to argue that this could make études a viable alternative to exercises, since they offer the possibility of richer, more creative problem-solving activity, with comparable effectiveness in developing procedural fluency. This is a key finding, as it means with these kinds of activities you get the best of both words. Indeed, Foster (2013) presents the diagram on the next page, which illustrates the vital role that the very best études and Purposeful Practice activities play.

Too often I would move from the top-left to the bottom-right before my students were ready, and completely neglect the possibility of something existing in the top-right.

What I do now

When introducing a topic or a concept for the first time, I follow a model of Deliberate Practice, encompassing Chapter 4’s presentation of information, with Chapters 6 and 7’s choice and delivery of examples and practice questions. This is true of completely brand new concepts, such as histograms and graphs of trigonometric functions, and also concepts that are essentially extensions of concepts students have previously studied, such as enlargements with negative scale factors and solving more complex linear equations. Here I want to provide plenty of structured support for my students, and I can do this because their prior experience and knowledge of the topic are similarly limited. I will also do the same if my formative assessment strategy (see Chapter 11) reveals significant difficulties across the majority of the class with any topic students have previously met before. Whilst not ideal, here I feel it is probably best to start from square one.

Figure 10.2 – Source: Colin Foster (2013)

However, when reviewing a topic or concept that I know students have encountered in its entirety, and that the majority of students clearly have some existing knowledge of, I need something else. The need is similar in the lessons immediately following the introduction of a concept, where some students need more straightforward practice and others are ready to push on. Here I will do a quick example-problem pair, both to show students how to set their work out and provide support for those struggling, followed by Purposeful Practice.

There are plenty of places to find Purposeful Practice activities, but no place (at the time of writing) that just contains them. For an activity to fit underneath the umbrella of Purposeful Practice, it must meet the five key principles I discussed above:

  1. Students need to experience early success
  2. There must be plenty of opportunities to practice the key procedure
  3. The practice should feel different
  4. Opportunities must exist for students to make connections, solve problems and think deeper
  5. The focus is always on the practice

Don Steward’s outrageously good Median Maths blog, NRICH, the Shell Centre, and Open-Middle problems are my top 4 places to visit in search of these magical tasks.

Keep the above criteria in mind when considering some of my favourite Purposeful Practice activities:

Factor Facts

Basic procedure practised: Working out the factors of a number

Figure 10.3 – Source: Don Steward, available at http://donsteward.blogspot.ae/2012/12/factor-facts.html

Don Steward is the king of Purposeful Practice, with many of his activities fitting my stringent criteria. For example, take this beauty on finding factors – something that students have been practising from age 9, and yet still often require help with. Here that practice is induced by means of a couple of simple looking challenges. There is no way students can complete this challenge without practising the exact skill I need them to practise. If they are struggling to start, I can help them experience immediate success by suggesting that they begin by writing down the number of factors each number has, starting with 1. At different stages through this activity, students begin to spot connections, have insights, and think deeper. They realise that they can save time by crossing out prime numbers and square numbers. They may notice a relationship between the prime factors of a number and the number of factors of that number. All the while they are practising finding factors – lots of them – and hence the main purpose of the activity is never lost.

Creating equations

Basic procedure practised: Solving linear equations

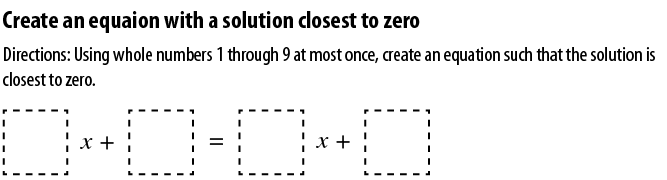
Figure 10.4 – Source: Robert Kaplinski for Open-Middle, available at http://www.openmiddle.com/solving-equations-with-variables-on-both-sides/

Here we have students practising the basics of solving linear equations, but again with a wider purpose. How close to zero can they get? How do they know how far off they are? And then we can push students further. How close to 1 can they get? What is the biggest value of x? How about the smallest? What if we could only use the numbers 1 to 5? What if the right-hand side of the equation was – x?

Area v Perimeter

Basic procedure practised: Working out the area and perimeter of rectilinear shapes

Figure 10.5 – Source: Malcolm Swan, available at http://blog.mrmeyer.com/2011/other-peoples-problems

When I first starting working on this book, I heard the sad news that Malcolm Swan had passed away. Malcolm was one of my true heroes, and through his incredible work at The Shell Centre and via the Improving Learning in Mathematics (also known as The Standards Units) materials, he has influenced generations of maths teachers and their lucky students. This is one of my favourite of Malcolm’s activities. We will discuss when it is appropriate to combine related topics such as area and perimeter in Chapter 12, but for now let us revel in the practice students get at working out the area and perimeter of the various rectilinear shapes they create in their quest to fill up the grid with points. Which points on the grid represent squares, rectangles, etc? Can you draw a shape that may be represented by the point (4, 12) or (12, 4)? Which points are impossible? Thank you, Malcolm.

Venn Diagrams

Basic procedure practised: Working out mean, median mode and range from a list of numbers

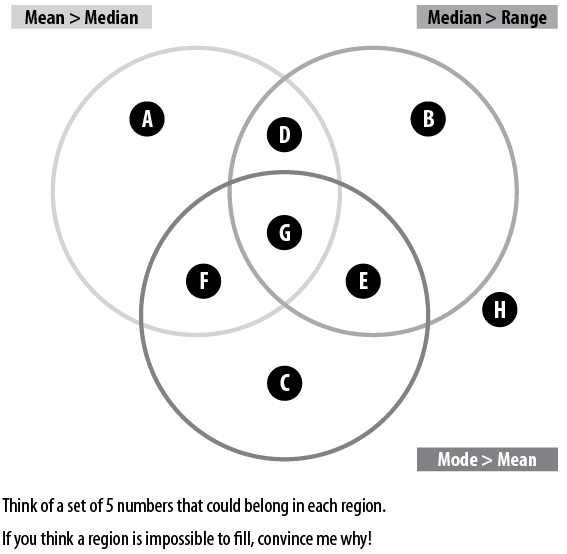
Figure 10.6 – Source: Craig Barton, available at http://mrbartonmaths.com/teachers/rich-tasks/venn-diagrams.html

Now, seeing as I created this activity, I don’t really want to wax lyrical too much about its virtues. However, it is worth sharing one thing I absolutely love about activities structured around Venn Diagrams – they are easy to get started, and difficult to finish. If a student says they are stuck on the activity above, then tell them to think of any five numbers. The beauty is, these five numbers must belong inside one of the eight regions. And once they have figured out where they go, they are away! The activity then gets harder and harder as students strive to fill the remaining regions, all the time delivering valuable practice working both forwards and backwards to calculate mean, median, mode and range, as well as the effect changing a number has on each of the measures of average and range. Are some of the regions impossible? If so, how do students know? And if students do finish, then no need to find them another activity. Simply challenge them to create their own Venn Diagram activity with a specified number of impossible regions.