Chapter 16
Continuing Research: The Doctoral Research on the S&P 500
At the beginning of the doctoral program, the folks running the institutions of higher education tell all the students to begin thinking about the subject of their dissertation. We call it the “big D.” It's not divorce, and it's not Dallas; it's the horrible thought of several more years of research. It's the really, really “BIG D.”
Just to bring you up to date on the academic parameters, a doctoral program or a Ph.D. program is all about research. As I mentioned in the introduction, the difference between a Ph.D. degree and a doctoral degree is that the Ph.D. develops the theory and the doctor with a doctoral degree tries to put that theory into practical use. Just to confuse things, both these academic designations carry the title of “Doctor.” The Ph.D. is just a bit more of a theoretical degree.
Some universities would rather not have doctors with doctoral degrees teaching their students. They would rather employ teachers that have the Ph.D. designation. I once had an instructor tell me that the university was in existence to teach the theoretical. Anything practical should be taught in technical schools. Oh yes, I was as shocked as those of you reading this.
Please don't forget that I began my doctoral education rather late in life. I went to a school where most of the students were middle-aged, with half of them coming from the teaching profession and the other half coming from industry. Those coming from the business world were mostly successful people in business who wanted the Holy Grail of degrees and to also learn some theory they could possibly put to practical use.
Why did I just tell you all this? I wanted to write my dissertation on a subject that I could use in real life and not just any subject to make my professors happy. I really wanted to take the theory, apply it, and construct a better portfolio for myself. Or to put it another way, use my education in order to make money. I guess I'm just a selfish, capitalistic individual.
The dissertation is a very large research paper usually completed after all the doctoral coursework is completed. The dissertation is several hundred pages of research along with many, many pages of supporting documentation. It is based on existing research work, and the job of the Ph.D. or doctoral candidate is to add to that body of knowledge.
My problem was I didn't know of any research performed on the method I had come into contact with through that seminar I once attended. Thus, I couldn't add to the body of knowledge that possibly didn't exist. I didn't even know the name of the method, which meant I couldn't even begin my search.
Finally, a Lead for Clean Surplus Accounting—Buffett, Graham, Ohlson
I know I talked about the following in the Introduction, but many of you probably didn't read the Introduction, so I think it is worth mentioning once again. By the way, the Introduction is a pretty good sea story in its own right.
I investigated the published research archives for about a year-and-a-half and finally found some information on the “phantom” method I came into contact with through that seminar I had once attended. It was called Clean Surplus Accounting and, folks, I am being totally speculative on the following.
A paper was published in 1989 by James Ohlson on how the Clean Surplus relation could be used in security valuation. Ohlson wrote his paper while at Columbia University. Does anyone remember where Warren Buffett went to school for his master's degree? And does anyone remember whom he studied under while getting his master's degree? Warren Buffett went to Columbia University and studied under Benjamin Graham, who is known as the “Father of Security Analysis.”
Again, I'm not implying anything here, but the three of these gentlemen gracing the academic halls of the same school certainly makes for good cocktail party conversation.
The Results of the Research
The following is an excerpt of an article I wrote regarding the test results of a section of my dissertation work:
The purpose of this test is to determine if portfolios constructed using a high average return on equity (ROE) configured using Clean Surplus Accounting are able to outperform the S&P 500 Index.
Methodology
As I said in the last chapter, methodology is a neat word, which summarizes the rules, framework, parameters, or system(s) set in place before the testing begins. Here are the rules for the research on Clean Surplus ROE and the S&P 500: Yes, Beyond Buffett.
1. A spreadsheet was developed for each security used in this test, such as the spreadsheet for Tupperware (TUP) in Table 16.1. The yearly net income (earnings before extraordinary write-offs and future liabilities) and dividends were used in order to obtain Clean Surplus book value (owners' equity).
Table 16.1 Tupperware (TUP) 3.3%
| Year | Owners' Equity | Net Income | Dividends Paid | Return on Equity |
| 2015 | $21.32 | $6.10 | $3.00 | 28.6% |
| 2014 | $18.84 | $5.20 | $2.72 | 27.6% |
| 2013 | $16.15 | $5.17 | $2.48 | 32.0% |
| 2012 | $14.17 | $3.42 | $1.44 | 24.1% |
| 2011 | $11.82 | $3.55 | $1.20 | 30.0% |
| 2010 | $9.29 | $3.53 | $1.00 | 38.0% |
| 2009 | $7.45 | $2.75 | $0.91 | 36.9% |
| 2008 | $5.77 | $2.56 | $0.88 | 44.4% |
Note: These numbers are very difficult to obtain during any current period. Thus, the data I have going back to 1982 is very probably the only early data in existence at the present time. This data, along with continuing data, form the basis of calculations for the computer program.
2. The securities used began with the S&P 500 as of December 1982. This list was narrowed due to several limitations. Securities not included in the sample consist of any security that did not include data for the entire sample period of 1982 through 1998. Any companies that merged or were dropped from the index were eliminated from the sample. The final sample consisted of 351 securities.
Notice Tupperware is not calculated in Tables 16.1 and 16.2 for the initial test periods, as I'm just using Tupperware as an example.
3. For the first test period, an eight-year time series average of the ROE of each stock was calculated using the Clean Surplus Accounting method, beginning in 1982 and continuing through 1989.
With Tupperware in Table 16.2, you will see the eight-year average ROE to be 32.7 percent.
Table 16.2 Tupperware (TUP) 3.3%
| Year | Owners' Equity | Net Income | Dividends Paid | Return on Equity |
| 2015 | $21.32 | $6.10 | $3.00 | 28.6% |
| 2014 | $18.84 | $5.20 | $2.72 | 27.6% |
| 2013 | $16.15 | $5.17 | $2.48 | 32.0% |
| 2012 | $14.17 | $3.42 | $1.44 | 24.1% |
| 2011 | $11.82 | $3.55 | $1.20 | 30.0% |
| 2010 | $9.29 | $3.53 | $1.00 | 38.0% |
| 2009 | $7.45 | $2.75 | $0.91 | 36.9% |
| 2008 | $5.77 | $2.56 | $0.88 | 44.4% |
| 8 Year Average ROE | 32.7% | |||
4. The total return calculations (price appreciation plus dividends) of each stock were calculated over the following four years. Thus, we obtained an eight-year average ROE, and we are trying to see if this average ROE has any bearing on the following four years of total returns (price appreciation plus dividends).
Note: The four-year returns began with the last day of March in order to fully incorporate into the price all earnings announcements for the previous year's fourth quarter. All fourth quarter earnings results are announced by the end of the following first quarter, with most of the announcements occurring during January of the first quarter. Thus, all announcements are fully incorporated into security value by the end of the first quarter of the year.
5. For the second test period, an eight-year period of average ROEs was calculated from 1986 through the end of 1993, followed by a four-year period of total returns (price appreciation plus dividends), beginning the end of March 1994 through end of March 1998.
Notice the Difference
In the following S&P 500 tests, I used an average ROE over eight years to try and predict the average yearly total return (price appreciation plus dividends) over the following four years. With the Dow tests of the previous chapter, I used a one-year ROE to select a portfolio that would outperform the Dow averages over the following one year.
Standardized Against the Market
The term “market returns” is meant to be the returns of the S&P 500 for the purposes of this study. The average ROE of all the S&P stocks in the study becomes the market ROE.
Portfolio Construction
1. The 351 securities were sorted in descending order of each stock's eight-year average ROEs for the first period of 1982–1989. Portfolios consisting of 10 stocks each were selected, beginning with the 10 stocks exhibiting the 10 highest average ROEs. The second portfolio consisted of the stocks with the next 10 highest ROEs. The average ROE of each 10-tock portfolio was used as a predictor against the total return of each portfolio for the subsequent four years of 1990–1994.
2. A second selection of portfolios chosen in the same manner was used with average ROEs of the eight-year period of 1986 through 1993 as a predictor of total returns for the period from the end of March 1994 through end of March 1998.
3. All stocks and portfolios were adjusted for risk. Risk was determined by beta (the most widely accepted measure of investment risk) obtained from Value Line. Total returns were divided by beta to obtain risk-adjusted returns.
Note: Beware of your source for beta. Beta will be different depending upon the period of measurement and duration of the periods. A source measuring stock results weekly over a five-year period will be different than measuring stock results monthly over the same five-year period.
The main purpose of this research is to determine if portfolios constructed with stocks of above-average ROEs as calculated by the Clean Surplus Method can outperform the S&P 500 Index.
Results: First Test Period
Table 16.3 shows the portfolio results of the first test period. These results include 14 portfolios, all of which had an average portfolio ROE greater than the average ROE of all the S&P 500 stocks in the test. In other words, they are portfolios with above-average ROEs.
Table 16.3 First Test Period Results
| 8 Yr. Avg. ROE
1982–1989 |
Avg. Yearly Risk-Adjusted Returns
3/31/90–3/31/94 |
Returns Above S&P | |
| 10-Stock Portfolio | |||
| S&P 500 | 10.35% | ||
| 1 | 53.5% | 26.1% | 15.8% |
| 2 | 31.9% | 13.7% | 3.4% |
| 3 | 27.0% | 15.9% | 5.5% |
| 4 | 24.6% | 26.9% | 16.5% |
| 5 | 22.5% | 16.4% | 6.1% |
| 6 | 21.4% | 18.0% | 7.7% |
| 7 | 20.7% | 18.3% | 7.9% |
| 8 | 20.0% | 14.6% | 4.2% |
| 9 | 19.6% | 26.2% | 15.9% |
| 10 | 19.9% | 16.9% | 6.5% |
| 11 | 18.4% | 17.6% | 7.3% |
| 12 | 17.8% | 23.5% | 13.1% |
| 13 | 17.3% | 25.8% | 15.5% |
| 14 | 16.4% | 20.6% | 10.3% |
Each portfolio's average ROE (the average of the ROEs of the stocks in each portfolio) from 1982 through 1989 is followed by the risk-adjusted average per year return of end of March 1990 through end of March 1994.
The S&P returned an average of 10.35 percent per year during this time frame. Every one of the portfolios with above-average ROEs outperformed the S&P 500.
Results: Second Test Period
The results of the second test period are shown in Table 16.4. Each portfolio's average ROE from 1986 through 1993 is followed by the risk-adjusted average per year return of end of March 1994 through end of March 1998.
Table 16.4 Second Test Period Results
| 8 Yr. Avg. ROE
1986–1993 |
Avg. Yearly Risk-Adjusted Returns
3/31/94–3/31/98 |
Returns Above S&P | |
| 10-Stock Portfolio | |||
| S&P 500 | 28.7% | ||
| 1 | 39.9% | 39.0% | 10.4% |
| 2 | 31.3% | 37.8% | 9.1% |
| 3 | 27.0% | 49.5% | 20.8% |
| 4 | 23.9% | 37.7% | 9.0% |
| 5 | 21.9% | 31.9% | 3.2% |
| 6 | 20.8% | 51.5% | 22.9% |
| 7 | 20.1% | 45.4% | 16.8% |
| 8 | 19.4% | 55.1% | 26.4% |
| 9 | 18.9% | 36.8% | 8.1% |
| 10 | 18.3% | 34.2% | 5.6% |
| 11 | 17.6% | 33.3% | 4.6% |
| 12 | 16.7% | 36.9% | 8.2% |
| 13 | 16.1% | 42.5% | 13.9% |
| 14 | 15.4% | 33.1% | 4.4% |
The S&P returned 28.7 percent per year during this time frame. Every portfolio that had an average ROE above the total average portfolio ROE outperformed the S&P 500.
Bias
There may be a survivorship bias. Many portfolios outperformed the S&P during the test periods. However, 500 stocks (the entire index) began in 1982, but just 351 securities survived the entire test period. It may be assumed that the securities that did not survive the entire test period were laggard performers, which, of course, is probably why many (if not all) of them are not in the index today.
Large Cap Bias
The S&P 500 is primarily a large cap (large capitalization) index. Thus, we cannot be certain that this strategy works well with smaller issues or stocks with less than an eight-year history of earnings.
Summary of Results
This initial work shows that the level of portfolio ROE with owners' equity configured by Clean Surplus Accounting does indeed have a direct relation to the level of future total returns.
The portfolios selected from the S&P 500 with higher average ROEs than the average portfolio did indeed outperform the market averages. In these test periods, all portfolios with above-average ROEs as configured by Clean Surplus Accounting outperformed the S&P 500 Index.
I don't know about you, but these tests show some pretty interesting results relative to predictability. These results show that the system works in average markets (first test period) and super bull markets, as in the second test period.
The Dow research in Chapter 15 (especially years 2000, 2001, and 2002) indicates that the predictability of better performance also holds true in horrible markets. Not that the stocks always have positive returns, but in our research, the returns of portfolios with higher than average ROE stocks (Clean Surplus) do better than portfolios of stocks with lower than average ROEs when the ROEs are configured by the Clean Surplus method.
Note: Only portfolios with higher than average ROEs are shown in this chapter.
Other Work
Work was also performed with portfolios of 30 stocks each (Figures 16.1 and 16.2). The results for the larger portfolios (30 stocks) were even more predictable and much more consistent than with the portfolios of 10 securities. For the statisticians reading this, the tests on larger portfolios of 30 securities showed a 79–80 percent correlation of portfolio ROEs and future total returns.
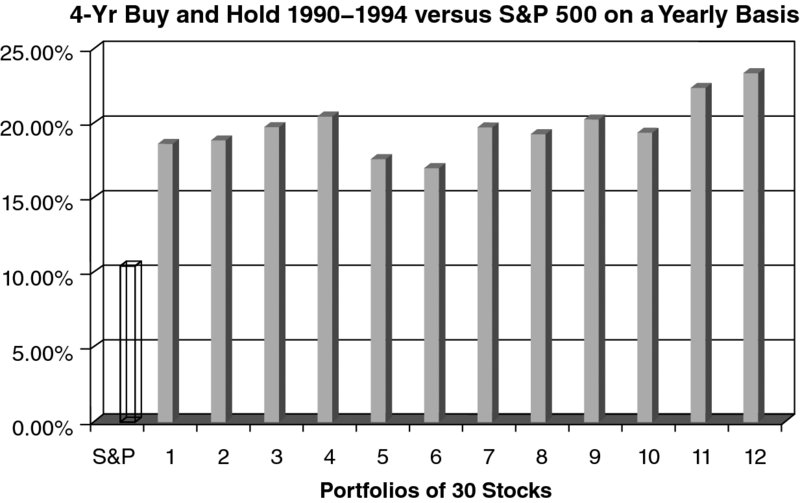
Figure 16.1 First Test Period of 30-Stock Portfolios
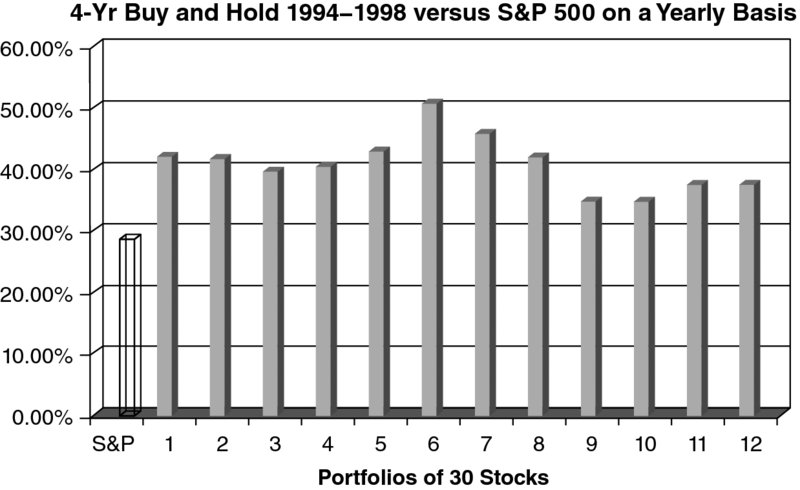
Figure 16.2 Second Test Period of 30-Stock Portfolios
- The first 30-stock portfolio was formed by combining the first three 10-tock portfolios. The second 30-tock portfolio was formed by combining the next three 10-tock portfolios and so on.
- The average return of the S&P 500 index over each four-year period is shown on the left in Figures 16.1 and 16.2.
- All of the 30-stock portfolios with above-average (above the S&P ROE) ROEs are shown to the right of the S&P and numbered 1 to 12.