

Not worth a pastis—Quételet’s error—The average man is a monster—Let’s deify it—Yes or no—Not so literary an experiment
Forget everything you heard in college statistics or probability theory. If you never took such a class, even better. Let us start from the very beginning.
I was transiting through the Frankfurt airport in December 2001, on my way from Oslo to Zurich.
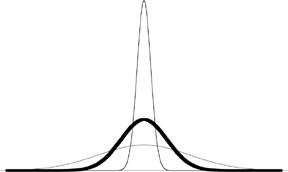
I had time to kill at the airport and it was a great opportunity for me to buy dark European chocolate, especially since I have managed to successfully convince myself that airport calories don’t count. The cashier handed me, among other things, a ten deutschmark bill, an (illegal) scan of which can be seen on the next page. The deutschmark banknotes were going to be put out of circulation in a matter of days, since Europe was switching to the euro. I kept it as a valedictory. Before the arrival of the euro, Europe had plenty of national currencies, which was good for printers, money changers, and of course currency traders like this (more or less) humble author. As I was eating my dark European chocolate and wistfully looking at the bill, I almost choked. I suddenly noticed, for the first time, that there was something curious about it. The bill bore the portrait of Carl Friedrich Gauss and a picture of his Gaussian bell curve.

The last ten deutschmark bill, representing Gauss and, to his right, the bell curve of Mediocristan.
The striking irony here is that the last possible object that can be linked to the German currency is precisely such a curve: the reichsmark (as the currency was previously called) went from four per dollar to four trillion per dollar in the space of a few years during the 1920s, an outcome that tells you that the bell curve is meaningless as a description of the randomness in currency fluctuations. All you need to reject the bell curve is for such a movement to occur once, and only once—just consider the consequences. Yet there was the bell curve, and next to it Herr Professor Doktor Gauss, unprepossessing, a little stern, certainly not someone I’d want to spend time with lounging on a terrace, drinking pastis, and holding a conversation without a subject.
Shockingly, the bell curve is used as a risk-measurement tool by those regulators and central bankers who wear dark suits and talk in a boring way about currencies.
The main point of the Gaussian, as I’ve said, is that most observations hover around the mediocre, the average; the odds of a deviation decline faster and faster (exponentially) as you move away from the average. If you must have only one single piece of information, this is the one: the dramatic increase in the speed of decline in the odds as you move away from the center, or the average. Look at the list below for an illustration of this. I am taking an example of a Gaussian quantity, such as height, and simplifying it a bit to make it more illustrative. Assume that the average height (men and women) is 1.67 meters, or 5 feet 7 inches. Consider what I call a unit of deviation here as 10 centimeters. Let us look at increments above 1.67 meters and consider the odds of someone being that tall.*
10 centimeters taller than the average (i.e., taller than 1.77 m, or 5 feet 10): 1 in 6.3
20 centimeters taller than the average (i.e., taller than 1.87 m, or 6 feet 2): 1 in 44
30 centimeters taller than the average (i.e., taller than 1.97 m, or 6 feet 6): 1 in 740
40 centimeters taller than the average (i.e., taller than 2.07 m, or 6 feet 9): 1 in 32,000
50 centimeters taller than the average (i.e., taller than 2.17 m, or 7 feet 1): 1 in 3,500,000
60 centimeters taller than the average (i.e., taller than 2.27 m, or 7 feet 5): 1 in 1,000,000,000
70 centimeters taller than the average (i.e., taller than 2.37 m, or 7 feet 9): 1 in 780,000,000,000
80 centimeters taller than the average (i.e., taller than 2.47 m, or 8 feet 1): 1 in 1,600,000,000,000,000
90 centimeters taller than the average (i.e., taller than 2.57 m, or 8 feet 5): 1 in 8,900,000,000,000,000,000
100 centimeters taller than the average (i.e., taller than 2.67 m, or 8 feet 9): 1 in 130,000,000,000,000,000,000,000
… and,
110 centimeters taller than the average (i.e., taller than 2.77 m, or 9 feet 1): 1 in 36,000,000,000,000,000,000,000,000,000,000,000, 000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, 000,000,000.
Note that soon after, I believe, 22 deviations, or 220 centimeters taller than the average, the odds reach a googol, which is 1 with 100 zeroes behind it.
The point of this list is to illustrate the acceleration. Look at the difference in odds between 60 and 70 centimeters taller than average: for a mere increase of four inches, we go from one in 1 billion people to one in 780 billion! As for the jump between 70 and 80 centimeters: an additional 4 inches above the average, we go from one in 780 billion to one in 1.6 million billion!*
This precipitous decline in the odds of encountering something is what allows you to ignore outliers. Only one curve can deliver this decline, and it is the bell curve (and its nonscalable siblings).
By comparison, look at the odds of being rich in Europe. Assume that wealth there is scalable, i.e., Mandelbrotian. (This is not an accurate description of wealth in Europe; it is simplified to emphasize the logic of scalable distribution.)†
People with a net worth higher than €1 million: 1 in 62.5
Higher than €2 million: 1 in 250
Higher than €4 million: 1 in 1,000
Higher than €8 million: 1 in 4,000
Higher than €16 million: 1 in 16,000
Higher than €32 million: 1 in 64,000
Higher than €320 million: 1 in 6,400,000
The speed of the decrease here remains constant (or does not decline)! When you double the amount of money you cut the incidence by a factor of four, no matter the level, whether you are at €8 million or €16 million. This, in a nutshell, illustrates the difference between Mediocristan and Extremistan.
Recall the comparison between the scalable and the nonscalable in Chapter 3. Scalability means that there is no headwind to slow you down.
Of course, Mandelbrotian Extremistan can take many shapes. Consider wealth in an extremely concentrated version of Extremistan; there, if you double the wealth, you halve the incidence. The result is quantitatively different from the above example, but it obeys the same logic.
People with a net worth higher than €1 million: 1 in 63
Higher than €2 million: 1 in 125
Higher than €4 million: 1 in 250
Higher than €8 million: 1 in 500
Higher than €16 million: 1 in 1,000
Higher than €32 million: 1 in 2,000
Higher than €320 million: 1 in 20,000
Higher than €640 million: 1 in 40,000
If wealth were Gaussian, we would observe the following divergence away from €1 million.
People with a net worth higher than €1 million: 1 in 63
Higher than €2 million: 1 in 127,000
Higher than €3 million: 1 in 14,000,000,000
Higher than €4 million: 1 in 886,000,000,000,000,000
Higher than €8 million: 1 in 16,000,000,000,000,000,000,000,000,000,000,000
Higher than €16 million: 1 in … none of my computers is capable of handling the computation.
What I want to show with these lists is the qualitative difference in the paradigms. As I have said, the second paradigm is scalable; it has no headwind. Note that another term for the scalable is power laws.
Just knowing that we are in a power-law environment does not tell us much. Why? Because we have to measure the coefficients in real life, which is much harder than with a Gaussian framework. Only the Gaussian yields its properties rather rapidly. The method I propose is a general way of viewing the world rather than a precise solution.
Remember this: the Gaussian–bell curve variations face a headwind that makes probabilities drop at a faster and faster rate as you move away from the mean, while “scalables,” or Mandelbrotian variations, do not have such a restriction. That’s pretty much most of what you need to know.*
Let us look more closely at the nature of inequality. In the Gaussian framework, inequality decreases as the deviations get larger—caused by the increase in the rate of decrease. Not so with the scalable: inequality stays the same throughout. The inequality among the superrich is the same as the inequality among the simply rich—it does not slow down.†
Consider this effect. Take a random sample of any two people from the U.S. population who jointly earn $1 million per annum. What is the most likely breakdown of their respective incomes? In Mediocristan, the most likely combination is half a million each. In Extremistan, it would be $50,000 and $950,000.
The situation is even more lopsided with book sales. If I told you that two authors sold a total of a million copies of their books, the most likely combination is 993,000 copies sold for one and 7,000 for the other. This is far more likely than that the books each sold 500,000 copies. For any large total, the breakdown will be more and more asymmetric.
Why is this so? The height problem provides a comparison. If I told you that the total height of two people is fourteen feet, you would identify the most likely breakdown as seven feet each, not two feet and twelve feet; not even eight feet and six feet! Persons taller than eight feet are so rare that such a combination would be impossible.
Have you ever heard of the 80/20 rule? It is the common signature of a power law—actually it is how it all started, when Vilfredo Pareto made the observation that 80 percent of the land in Italy was owned by 20 percent of the people. Some use the rule to imply that 80 percent of the work is done by 20 percent of the people. Or that 80 percent worth of effort contributes to only 20 percent of results, and vice versa.
As far as axioms go, this one wasn’t phrased to impress you the most: it could easily be called the 50/01 rule, that is, 50 percent of the work comes from 1 percent of the workers. This formulation makes the world look even more unfair, yet the two formulae are exactly the same. How? Well, if there is inequality, then those who constitute the 20 percent in the 80/20 rule also contribute unequally—only a few of them deliver the lion’s share of the results. This trickles down to about one in a hundred contributing a little more than half the total.
The 80/20 rule is only metaphorical; it is not a rule, even less a rigid law. In the U.S. book business, the proportions are more like 97/20 (i.e., 97 percent of book sales are made by 20 percent of the authors); it’s even worse if you focus on literary nonfiction (twenty books of close to eight thousand represent half the sales).
Note here that it is not all uncertainty. In some situations you may have a concentration, of the 80/20 type, with very predictable and tractable properties, which enables clear decision making, because you can identify beforehand where the meaningful 20 percent are. These situations are very easy to control. For instance, Malcolm Gladwell wrote in an article in The New Yorker that most abuse of prisoners is attributable to a very small number of vicious guards. Filter those guards out and your rate of prisoner abuse drops dramatically. (In publishing, on the other hand, you do not know beforehand which book will bring home the bacon. The same with wars, as you do not know beforehand which conflict will kill a portion of the planet’s residents.)
I’ll summarize here and repeat the arguments previously made throughout the book. Measures of uncertainty that are based on the bell curve simply disregard the possibility, and the impact, of sharp jumps or discontinuities and are, therefore, inapplicable in Extremistan. Using them is like focusing on the grass and missing out on the (gigantic) trees. Although unpredictable large deviations are rare, they cannot be dismissed as outliers because, cumulatively, their impact is so dramatic.
The traditional Gaussian way of looking at the world begins by focusing on the ordinary, and then deals with exceptions or so-called outliers as ancillaries. But there is a second way, which takes the exceptional as a starting point and treats the ordinary as subordinate.
I have emphasized that there are two varieties of randomness, qualitatively different, like air and water. One does not care about extremes; the other is severely impacted by them. One does not generate Black Swans; the other does. We cannot use the same techniques to discuss a gas as we would use with a liquid. And if we could, we wouldn’t call the approach “an approximation.” A gas does not “approximate” a liquid.
We can make good use of the Gaussian approach in variables for which there is a rational reason for the largest not to be too far away from the average. If there is gravity pulling numbers down, or if there are physical limitations preventing very large observations, we end up in Mediocristan. If there are strong forces of equilibrium bringing things back rather rapidly after conditions diverge from equilibrium, then again you can use the Gaussian approach. Otherwise, fuhgedaboudit. This is why much of economics is based on the notion of equilibrium: among other benefits, it allows you to treat economic phenomena as Gaussian.
Note that I am not telling you that the Mediocristan type of randomness does not allow for some extremes. But it tells you that they are so rare that they do not play a significant role in the total. The effect of such extremes is pitifully small and decreases as your population gets larger.
To be a little bit more technical here, if you have an assortment of giants and dwarfs, that is, observations several orders of magnitude apart, you could still be in Mediocristan. How? Assume you have a sample of one thousand people, with a large spectrum running from the dwarf to the giant. You are likely to see many giants in your sample, not a rare occasional one. Your average will not be impacted by the occasional additional giant because some of these giants are expected to be part of your sample, and your average is likely to be high. In other words, the largest observation cannot be too far away from the average. The average will always contain both kinds, giants and dwarves, so that neither should be too rare—unless you get a megagiant or a microdwarf on very rare occasion. This would be Mediocristan with a large unit of deviation.
Note once again the following principle: the rarer the event, the higher the error in our estimation of its probability—even when using the Gaussian.
Let me show you how the Gaussian bell curve sucks randomness out of life—which is why it is popular. We like it because it allows certainties! How? Through averaging, as I will discuss next.
Recall from the Mediocristan discussion in Chapter 3 that no single observation will impact your total. This property will be more and more significant as your population increases in size. The averages will become more and more stable, to the point where all samples will look alike.
I’ve had plenty of cups of coffee in my life (it’s my principal addiction). I have never seen a cup jump two feet from my desk, nor has coffee spilled spontaneously on this manuscript without intervention (even in Russia). Indeed, it will take more than a mild coffee addiction to witness such an event; it would require more lifetimes than is perhaps conceivable—the odds are so small, one in so many zeroes, that it would be impossible for me to write them down in my free time.
Yet physical reality makes it possible for my coffee cup to jump—very unlikely, but possible. Particles jump around all the time. How come the coffee cup, itself composed of jumping particles, does not? The reason is, simply, that for the cup to jump would require that all of the particles jump in the same direction, and do so in lockstep several times in a row (with a compensating move of the table in the opposite direction). All several trillion particles in my coffee cup are not going to jump in the same direction; this is not going to happen in the lifetime of this universe. So I can safely put the coffee cup on the edge of my writing table and worry about more serious sources of uncertainty.
FIGURE 7: How the Law of Large Numbers Works

In Mediocristan, as your sample size increases, the observed average will present itself with less and less dispersion—as you can see, the distribution will be narrower and narrower. This, in a nutshell, is how everything in statistical theory works (or is supposed to work). Uncertainty in Mediocristan vanishes under averaging. This illustrates the hackneyed “law of large numbers.”
The safety of my coffee cup illustrates how the randomness of the Gaussian is tamable by averaging. If my cup were one large particle, or acted as one, then its jumping would be a problem. But my cup is the sum of trillions of very small particles.
Casino operators understand this well, which is why they never (if they do things right) lose money. They simply do not let one gambler make a massive bet, instead preferring to have plenty of gamblers make series of bets of limited size. Gamblers may bet a total of $20 million, but you needn’t worry about the casino’s health: the bets run, say, $20 on average; the casino caps the bets at a maximum that will allow the casino owners to sleep at night. So the variations in the casino’s returns are going to be ridiculously small, no matter the total gambling activity. You will not see anyone leaving the casino with $1 billion—in the lifetime of this universe.
The above is an application of the supreme law of Mediocristan: when you have plenty of gamblers, no single gambler will impact the total more than minutely.
The consequence of this is that variations around the average of the Gaussian, also called “errors,” are not truly worrisome. They are small and they wash out. They are domesticated fluctuations around the mean.
If you ever took a (dull) statistics class in college, did not understand much of what the professor was excited about, and wondered what “standard deviation” meant, there is nothing to worry about. The notion of standard deviation is meaningless outside of Mediocristan. Clearly it would have been more beneficial, and certainly more entertaining, to have taken classes in the neurobiology of aesthetics or postcolonial African dance, and this is easy to see empirically.
Standard deviations do not exist outside the Gaussian, or if they do exist they do not matter and do not explain much. But it gets worse. The Gaussian family (which includes various friends and relatives, such as the Poisson law) are the only class of distributions that the standard deviation (and the average) is sufficient to describe. You need nothing else. The bell curve satisfies the reductionism of the deluded.
There are other notions that have little or no significance outside of the Gaussian: correlation and, worse, regression. Yet they are deeply ingrained in our methods; it is hard to have a business conversation without hearing the word correlation.
To see how meaningless correlation can be outside of Mediocristan, take a historical series involving two variables that are patently from Extremistan, such as the bond and the stock markets, or two securities prices, or two variables like, say, changes in book sales of children’s books in the United States, and fertilizer production in China; or real-estate prices in New York City and returns of the Mongolian stock market. Measure correlation between the pairs of variables in different subperiods, say, for 1994, 1995, 1996, etc. The correlation measure will be likely to exhibit severe instability; it will depend on the period for which it was computed. Yet people talk about correlation as if it were something real, making it tangible, investing it with a physical property, reifying it.
The same illusion of concreteness affects what we call “standard” deviations. Take any series of historical prices or values. Break it up into subsegments and measure its “standard” deviation. Surprised? Every sample will yield a different “standard” deviation. Then why do people talk about standard deviations? Go figure.
Note here that, as with the narrative fallacy, when you look at past data and compute one single correlation or standard deviation, you do not notice such instability.
If you use the term statistically significant, beware of the illusions of certainties. Odds are that someone has looked at his observation errors and assumed that they were Gaussian, which necessitates a Gaussian context, namely, Mediocristan, for it to be acceptable.
To show how endemic the problem of misusing the Gaussian is, and how dangerous it can be, consider a (dull) book called Catastrophe by Judge Richard Posner, a prolific writer. Posner bemoans civil servants’ misunderstandings of randomness and recommends, among other things, that government policy makers learn statistics … from economists. Judge Posner appears to be trying to foment catastrophes. Yet, in spite of being one of those people who should spend more time reading and less time writing, he can be an insightful, deep, and original thinker; like many people, he just isn’t aware of the distinction between Mediocristan and Extremistan, and he believes that statistics is a “science,” never a fraud. If you run into him, please make him aware of these things.
This monstrosity called the Gaussian bell curve is not Gauss’s doing. Although he worked on it, he was a mathematician dealing with a theoretical point, not making claims about the structure of reality like statistical-minded scientists. G. H. Hardy wrote in “A Mathematician’s Apology”:
The “real” mathematics of the “real” mathematicians, the mathematics of Fermat and Euler and Gauss and Abel and Riemann, is almost wholly “useless” (and this is as true of “applied” as of “pure” mathematics).
As I mentioned earlier, the bell curve was mainly the concoction of a gambler, Abraham de Moivre (1667–1754), a French Calvinist refugee who spent much of his life in London, though speaking heavily accented English. But it is Quételet, not Gauss, who counts as one of the most destructive fellows in the history of thought, as we will see next.
Adolphe Quételet (1796–1874) came up with the notion of a physically average human, l’homme moyen. There was nothing moyen about Quételet, “a man of great creative passions, a creative man full of energy.” He wrote poetry and even coauthored an opera. The basic problem with Quételet was that he was a mathematician, not an empirical scientist, but he did not know it. He found harmony in the bell curve.
The problem exists at two levels. Primo, Quételet had a normative idea, to make the world fit his average, in the sense that the average, to him, was the “normal.” It would be wonderful to be able to ignore the contribution of the unusual, the “nonnormal,” the Black Swan, to the total. But let us leave that dream for utopia.
Secondo, there was a serious associated empirical problem. Quételet saw bell curves everywhere. He was blinded by bell curves and, I have learned, again, once you get a bell curve in your head it is hard to get it out. Later, Frank Ysidro Edgeworth would refer to Quételesmus as the grave mistake of seeing bell curves everywhere.
Quételet provided a much needed product for the ideological appetites of his day. As he lived between 1796 and 1874, so consider the roster of his contemporaries: Saint-Simon (1760–1825), Pierre-Joseph Proudhon (1809–1865), and Karl Marx (1818–1883), each the source of a different version of socialism. Everyone in this post-Enlightenment moment was longing for the aurea mediocritas, the golden mean: in wealth, height, weight, and so on. This longing contains some element of wishful thinking mixed with a great deal of harmony and … Platonicity.
I always remember my father’s injunction that in medio stat virtus, “virtue lies in moderation.” Well, for a long time that was the ideal; mediocrity, in that sense, was even deemed golden. All-embracing mediocrity.
But Quételet took the idea to a different level. Collecting statistics, he started creating standards of “means.” Chest size, height, the weight of babies at birth, very little escaped his standards. Deviations from the norm, he found, became exponentially more rare as the magnitude of the deviation increased. Then, having conceived of this idea of the physical characteristics of l’homme moyen, Monsieur Quételet switched to social matters. L’homme moyen had his habits, his consumption, his methods.
Through his construct of l’homme moyen physique and l’homme moyen moral, the physically and morally average man, Quételet created a range of deviance from the average that positions all people either to the left or right of center and, truly, punishes those who find themselves occupying the extreme left or right of the statistical bell curve. They became abnormal. How this inspired Marx, who cites Quételet regarding this concept of an average or normal man, is obvious: “Societal deviations in terms of the distribution of wealth for example, must be minimized,” he wrote in Das Kapital.
One has to give some credit to the scientific establishment of Quételet’s day. They did not buy his arguments at once. The philosopher/mathematician/economist Augustin Cournot, for starters, did not believe that one could establish a standard human on purely quantitative grounds. Such a standard would be dependent on the attribute under consideration. A measurement in one province may differ from that in another province. Which one should be the standard? L’homme moyen would be a monster, said Cournot. I will explain his point as follows.
Assuming there is something desirable in being an average man, he must have an unspecified specialty in which he would be more gifted than other people—he cannot be average in everything. A pianist would be better on average at playing the piano, but worse than the norm at, say, horseback riding. A draftsman would have better drafting skills, and so on. The notion of a man deemed average is different from that of a man who is average in everything he does. In fact, an exactly average human would have to be half male and half female. Quételet completely missed that point.
A much more worrisome aspect of the discussion is that in Quételet’s day, the name of the Gaussian distribution was la loi des erreurs, the law of errors, since one of its earliest applications was the distribution of errors in astronomic measurements. Are you as worried as I am? Divergence from the mean (here the median as well) was treated precisely as an error! No wonder Marx fell for Quételet’s ideas.
This concept took off very quickly. The ought was confused with the is, and this with the imprimatur of science. The notion of the average man is steeped in the culture attending the birth of the European middle class, the nascent post-Napoleonic shopkeeper’s culture, chary of excessive wealth and intellectual brilliance. In fact, the dream of a society with compressed outcomes is assumed to correspond to the aspirations of a rational human being facing a genetic lottery. If you had to pick a society to be born into for your next life, but could not know which outcome awaited you, it is assumed you would probably take no gamble; you would like to belong to a society without divergent outcomes.
One entertaining effect of the glorification of mediocrity was the creation of a political party in France called Poujadism, composed initially of a grocery-store movement. It was the warm huddling together of the semi-favored hoping to see the rest of the universe compress itself into their rank—a case of non-proletarian revolution. It had a grocery-store-owner mentality, down to the employment of the mathematical tools. Did Gauss provide the mathematics for the shopkeepers?
Poincaré himself was quite suspicious of the Gaussian. I suspect that he felt queasy when it and similar approaches to modeling uncertainty were presented to him. Just consider that the Gaussian was initially meant to measure astronomic errors, and that Poincaré’s ideas of modeling celestial mechanics were fraught with a sense of deeper uncertainty.
Poincaré wrote that one of his friends, an unnamed “eminent physicist,” complained to him that physicists tended to use the Gaussian curve because they thought mathematicians believed it a mathematical necessity; mathematicians used it because they believed that physicists found it to be an empirical fact.
Let me state here that, except for the grocery-store mentality, I truly believe in the value of middleness and mediocrity—what humanist does not want to minimize the discrepancy between humans? Nothing is more repugnant than the inconsiderate ideal of the Übermensch! My true problem is epistemological. Reality is not Mediocristan, so we should learn to live with it.
The list of people walking around with the bell curve stuck in their heads, thanks to its Platonic purity, is incredibly long.
Sir Francis Galton, Charles Darwin’s first cousin and Erasmus Darwin’s grandson, was perhaps, along with his cousin, one of the last independent gentlemen scientists—a category that also included Lord Cavendish, Lord Kelvin, Ludwig Wittgenstein (in his own way), and to some extent, our überphilosopher Bertrand Russell. Although John Maynard Keynes was not quite in that category, his thinking epitomizes it. Galton lived in the Victorian era when heirs and persons of leisure could, among other choices, such as horseback riding or hunting, become thinkers, scientists, or (for those less gifted) politicians. There is much to be wistful about in that era: the authenticity of someone doing science for science’s sake, without direct career motivations.
Unfortunately, doing science for the love of knowledge does not necessarily mean you will head in the right direction. Upon encountering and absorbing the “normal” distribution, Galton fell in love with it. He was said to have exclaimed that if the Greeks had known about it, they would have deified it. His enthusiasm may have contributed to the prevalence of the use of the Gaussian.
Galton was blessed with no mathematical baggage, but he had a rare obsession with measurement. He did not know about the law of large numbers, but rediscovered it from the data itself. He built the quincunx, a pinball machine that shows the development of the bell curve—on which, more in a few paragraphs. True, Galton applied the bell curve to areas like genetics and heredity, in which its use was justified. But his enthusiasm helped thrust nascent statistical methods into social issues.
Let me discuss here the extent of the damage. If you’re dealing with qualitative inference, such as in psychology or medicine, looking for yes/no answers to which magnitudes don’t apply, then you can assume you’re in Mediocristan without serious problems. The impact of the improbable cannot be too large. You have cancer or you don’t, you are pregnant or you are not, et cetera. Degrees of deadness or pregnancy are not relevant (unless you are dealing with epidemics). But if you are dealing with aggregates, where magnitudes do matter, such as income, your wealth, return on a portfolio, or book sales, then you will have a problem and get the wrong distribution if you use the Gaussian, as it does not belong there. One single number can disrupt all your averages; one single loss can eradicate a century of profits. You can no longer say “this is an exception.” The statement “Well, I can lose money” is not informational unless you can attach a quantity to that loss. You can lose all your net worth or you can lose a fraction of your daily income; there is a difference.
This explains why empirical psychology and its insights on human nature, which I presented in the earlier parts of this book, are robust to the mistake of using the bell curve; they are also lucky, since most of their variables allow for the application of conventional Gaussian statistics. When measuring how many people in a sample have a bias, or make a mistake, these studies generally elicit a yes/no type of result. No single observation, by itself, can disrupt their overall findings.
I will next proceed to a sui generis presentation of the bell-curve idea from the ground up.
Consider a pinball machine like the one shown in Figure 8. Launch 32 balls, assuming a well-balanced board so that the ball has equal odds of falling right or left at any juncture when hitting a pin. Your expected outcome is that many balls will land in the center columns and that the number of balls will decrease as you move to the columns away from the center.
Next, consider a gedanken, a thought experiment. A man flips a coin and after each toss he takes a step to the left or a step to the right, depending on whether the coin came up heads or tails. This is called the random walk, but it does not necessarily concern itself with walking. You could identically say that instead of taking a step to the left or to the right, you would win or lose $1 at every turn, and you will keep track of the cumulative amount that you have in your pocket.
Assume that I set you up in a (legal) wager where the odds are neither in your favor nor against you. Flip a coin. Heads, you make $1, tails, you lose $1.
At the first flip, you will either win or lose.
At the second flip, the number of possible outcomes doubles. Case one: win, win. Case two: win, lose. Case three: lose, win. Case four: lose, lose. Each of these cases has equivalent odds, the combination of a single win and a single loss has an incidence twice as high because cases two and three, win-lose and lose-win, amount to the same outcome. And that is the key for the Gaussian. So much in the middle washes out—and we will see that there is a lot in the middle. So, if you are playing for $1 a round, after two rounds you have a 25 percent chance of making or losing $2, but a 50 percent chance of breaking even.
FIGURE 8: THE QUINCUNX (SIMPLIFIED)—A PINBALL MACHINE

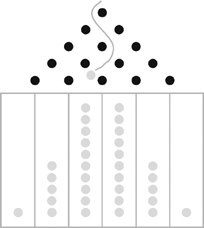
Drop balls that, at every pin, randomly fall right or left. Above Is the most probable scenario, which greatly resembles the bell curve (a.k.a. Gaussian disribution). Courtesy of Alexander Taleb.
Let us do another round. The third flip again doubles the number of cases, so we face eight possible outcomes. Case 1 (it was win, win in the second flip) branches out into win, win, win and win, win, lose. We add a win or lose to the end of each of the previous results. Case 2 branches out into win, lose, win and win, lose, lose. Case 3 branches out into lose, win, win and lose, win, lose. Case 4 branches out into lose, lose, win and lose, lose, lose.
We now have eight cases, all equally likely. Note that again you can group the middling outcomes where a win cancels out a loss. (In Galton’s quincunx, situations where the ball falls left and then falls right, or vice versa, dominate so you end up with plenty in the middle.) The net, or cumulative, is the following: 1) three wins; 2) two wins, one loss, net one win; 3) two wins, one loss, net one win; 4) one win, two losses, net one loss; 5) two wins, one loss, net one win; 6) two losses, one win, net one loss; 7) two losses, one win, net one loss; and, finally, 8) three losses.
Out of the eight cases, the case of three wins occurs once. The case of three losses occurs once. The case of one net loss (one win, two losses) occurs three times. The case of one net win (one loss, two wins) occurs three times.
Play one more round, the fourth. There will be sixteen equally likely outcomes. You will have one case of four wins, one case of four losses, four cases of two wins, four cases of two losses, and six break-even cases.
The quincunx (its name is derived from the Latin for five) in the pinball example shows the fifth round, with thirty-two possibilities, easy to track. Such was the concept behind the quincunx used by Francis Galton. Galton was both insufficiently lazy and a bit too innocent of mathematics; instead of building the contraption, he could have worked with simpler algebra, or perhaps undertaken a thought experiment like this one.
Let’s keep playing. Continue until you have forty flips. You can perform them in minutes, but we will need a calculator to work out the number of outcomes, which are taxing to our simple thought method. You will have about 1,099,511,627,776 possible combinations—more than one thousand billion. Don’t bother doing the calculation manually, it is two multiplied by itself forty times, since each branch doubles at every juncture. (Recall that we added a win and a lose at the end of the alternatives of the third round to go to the fourth round, thus doubling the number of alternatives.) Of these combinations, only one will be up forty, and only one will be down forty. The rest will hover around the middle, here zero.
We can already see that in this type of randomness extremes are exceedingly rare. One in 1,099,511,627,776 is up forty out of forty tosses. If you perform the exercise of forty flips once per hour, the odds of getting 40 ups in a row are so small that it would take quite a bit of forty-flip trials to see it. Assuming you take a few breaks to eat, argue with your friends and roommates, have a beer, and sleep, you can expect to wait close to four million lifetimes to get a 40-up outcome (or a 40-down outcome) just once. And consider the following. Assume you play one additional round, for a total of 41; to get 41 straight heads would take eight million lifetimes! Going from 40 to 41 halves the odds. This is a key attribute of the nonscalable framework to analyzing randomness: extreme deviations decrease at an increasing rate. You can expect to toss 50 heads in a row once in four billion lifetimes!
FIGURE 9: NUMBERS OF WINS TOSSED


Result of forty tosses. We see the proto-bell curve emerging.
We are not yet fully in a Gaussian bell curve, but we are getting dangerously close. This is still proto-Gaussian, but you can see the gist. (Actually, you will never encounter a Gaussian in its purity since it is a Platonic form—you just get closer but cannot attain it.) However, as you can see in Figure 9, the familiar bell shape is starting to emerge.
How do we get even closer to the perfect Gaussian bell curve? By refining the flipping process. We can either flip 40 times for $1 a flip or 4,000 times for ten cents a flip, and add up the results. Your expected risk is about the same in both situations—and that is a trick. The equivalence in the two sets of flips has a little nonintuitive hitch. We multiplied the number of bets by 100, but divided the bet size by 10—don’t look for a reason now, just assume that they are “equivalent.” The overall risk is equivalent, but now we have opened up the possibility of winning or losing 400 times in a row. The odds are about one in 1 with 120 zeroes after it, that is, one in 1,000,000,000,000,000,000,000,000,000,000,000,000, 000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, 000,000,000,000,000,000,000,000,000,000,000,000 times.
Continue the process for a while. We go from 40 tosses for $1 each to 4,000 tosses for 10 cents, to 400,000 tosses for 1 cent, getting close and closer to a Gaussian. Figure 10 shows results spread between −40 and 40, namely eighty plot points. The next one would bring that up to 8,000 points.
FIGURE 10: A MORE ABSTRACT VERSION: PLATO’S CURVE


An infinite number of tosses.
Let’s keep going. We can flip 4,000 times staking a tenth of a penny. How about 400,000 times at 1/1000 of a penny? As a Platonic form, the pure Gaussian curve is principally what happens when he have an infinity of tosses per round, with each bet infinitesimally small. Do not bother trying to visualize the results, or even make sense out of them. We can no longer talk about an “infinitesimal” bet size (since we have an infinity of these, and we are in what mathematicians call a continuous framework). The good news is that there is a substitute.
We have moved from a simple bet to something completely abstract. We have moved from observations into the realm of mathematics. In mathematics things have a purity to them.
Now, something completely abstract is not supposed to exist, so please do not even make an attempt to understand Figure 10. Just be aware of its use. Think of it as a thermometer: you are not supposed to understand what the temperature means in order to talk about it. You just need to know the correspondence between temperature and comfort (or some other empirical consideration). Sixty degrees corresponds to pleasant weather; ten below is not something to look forward to. You don’t necessarily care about the actual speed of the collisions among particles that more technically explains temperature. Degrees are, in a way, a means for your mind to translate some external phenomena into a number. Likewise, the Gaussian bell curve is set so that 68.2 percent of the observations fall between minus one and plus one standard deviations away from the average. I repeat: do not even try to understand whether standard deviation is average deviation—it is not, and a large (too large) number of people using the word standard deviation do not understand this point. Standard deviation is just a number that you scale things to, a matter of mere correspondence if phenomena were Gaussian.
These standard deviations are often nicknamed “sigma.” People also talk about “variance” (same thing: variance is the square of the sigma, i.e., of the standard deviation).
Note the symmetry in the curve. You get the same results whether the sigma is positive or negative. The odds of falling below −4 sigmas are the same as those of exceeding 4 sigmas, here 1 in 32,000 times.
As the reader can see, the main point of the Gaussian bell curve is, as I have been saying, that most observations hover around the mediocre, the mean, while the odds of a deviation decline faster and faster (exponentially) as you move away from the mean. If you need to retain one single piece of information, just remember this dramatic speed of decrease in the odds as you move away from the average. Outliers are increasingly unlikely. You can safely ignore them.
This property also generates the supreme law of Mediocristan: given the paucity of large deviations, their contribution to the total will be vanishingly small.
In the height example earlier in this chapter, I used units of deviations of ten centimeters, showing how the incidence declined as the height increased. These were one sigma deviations; the height table also provides an example of the operation of “scaling to a sigma” by using the sigma as a unit of measurement.
Note the central assumptions we made in the coin-flip game that led to the proto-Gaussian, or mild randomness.
First central assumption: the flips are independent of one another. The coin has no memory. The fact that you got heads or tails on the previous flip does not change the odds of your getting heads or tails on the next one. You do not become a “better” coin flipper over time. If you introduce memory, or skills in flipping, the entire Gaussian business becomes shaky.
Recall our discussions in Chapter 14 on preferential attachment and cumulative advantage. Both theories assert that winning today makes you more likely to win in the future. Therefore, probabilities are dependent on history, and the first central assumption leading to the Gaussian bell curve fails in reality. In games, of course, past winnings are not supposed to translate into an increased probability of future gains—but not so in real life, which is why I worry about teaching probability from games. But when winning leads to more winning, you are far more likely to see forty wins in a row than with a proto-Gaussian.
Second central assumption: no “wild” jump. The step size in the building block of the basic random walk is always known, namely one step. There is no uncertainty as to the size of the step. We did not encounter situations in which the move varied wildly.
Remember that if either of these two central assumptions is not met, your moves (or coin tosses) will not cumulatively lead to the bell curve. Depending on what happens, they can lead to the wild Mandelbrotian-style scale-invariant randomness.
One of the problems I face in life is that whenever I tell people that the Gaussian bell curve is not ubiquitous in real life, only in the minds of statisticians, they require me to “prove it”—which is easy to do, as we will see in the next two chapters, yet nobody has managed to prove the opposite. Whenever I suggest a process that is not Gaussian, I am asked to justify my suggestion and to, beyond the phenomena, “give them the theory behind it.” We saw in Chapter 14 the rich-get-richer models that were proposed in order to justify not using a Gaussian. Modelers were forced to spend their time writing theories on possible models that generate the scalable—as if they needed to be apologetic about it. Theory shmeory! I have an epistemological problem with that, with the need to justify the world’s failure to resemble an idealized model that someone blind to reality has managed to promote.
My technique, instead of studying the possible models generating non-bell curve randomness, hence making the same errors of blind theorizing, is to do the opposite: to know the bell curve as intimately as I can and identify where it can and cannot hold. I know where Mediocristan is. To me it is frequently (nay, almost always) the users of the bell curve who do not understand it well, and have to justify it, and not the opposite.
This ubiquity of the Gaussian is not a property of the world, but a problem in our minds, stemming from the way we look at it.
• • •
The next chapter will address the scale invariance of nature and address the properties of the fractal. The chapter after that will probe the misuse of the Gaussian in socioeconomic life and “the need to produce theories.”
I sometimes get a little emotional because I’ve spent a large part of my life thinking about this problem. Since I started thinking about it, and conducting a variety of thought experiments as I have above, I have not for the life of me been able to find anyone around me in the business and statistical world who was intellectually consistent in that he both accepted the Black Swan and rejected the Gaussian and Gaussian tools. Many people accepted my Black Swan idea but could not take it to its logical conclusion, which is that you cannot use one single measure for randomness called standard deviation (and call it “risk”); you cannot expect a simple answer to characterize uncertainty. To go the extra step requires courage, commitment, an ability to connect the dots, a desire to understand randomness fully. It also means not accepting other people’s wisdom as gospel. Then I started finding physicists who had rejected the Gaussian tools but fell for another sin: gullibility about precise predictive models, mostly elaborations around the preferential attachment of Chapter 14—another form of Platonicity. I could not find anyone with depth and scientific technique who looked at the world of randomness and understood its nature, who looked at calculations as an aid, not a principal aim. It took me close to a decade and a half to find that thinker, the man who made many swans gray: Mandelbrot—the great Benoît Mandelbrot.
* The nontechnical (or intuitive) reader can skip this chapter, as it goes into some details about the bell curve. Also, you can skip it if you belong to the category of fortunate people who do not know about the bell curve.
* I have fudged the numbers a bit for simplicity’s sake.
* One of the most misunderstood aspects of a Gaussian is its fragility and vulnerability in the estimation of tail events. The odds of a 4 sigma move are twice that of a 4.15 sigma. The odds of a 20 sigma are a trillion times higher than those of a 21 sigma! It means that a small measurement error of the sigma will lead to a massive underestimation of the probability. We can be a trillion times wrong about some events.
† My main point, which I repeat in some form or another throughout Part Three, is as follows. Everything is made easy, conceptually, when you consider that there are two, and only two, possible paradigms: nonscalable (like the Gaussian) and other (such as Mandebrotian randomness). The rejection of the application of the nonscalable is sufficient, as we will see later, to eliminate a certain vision of the world. This is like negative empiricism: I know a lot by determining what is wrong.
* Note that variables may not be infinitely scalable; there could be a very, very remote upper limit—but we do not know where it is so we treat a given situation as if it were infinitely scalable. Technically, you cannot sell more of one book than there are denizens of the planet—but that upper limit is large enough to be treated as if it didn’t exist. Furthermore, who knows, by repackaging the book, you might be able to sell it to a person twice, or get that person to watch the same movie several times.
† As I was revising this draft, in August 2006, I stayed at a hotel in Dedham, Massachusetts, near one of my children’s summer camps. There, I was a little intrigued by the abundance of weight-challenged people walking around the lobby and causing problems with elevator backups. It turned out that the annual convention of NAFA, the National Association for Fat Acceptance, was being held there. As most of the members were extremely overweight, I was not able to figure out which delegate was the heaviest: some form of equality prevailed among the very heavy (someone much heavier than the persons I saw would have been dead). I am sure that at the NARA convention, the National Association for Rich Acceptance, one person would dwarf the others, and, even among the superrich, a very small percentage would represent a large section of the total wealth.