Cognitive knowledge learning (CKL) is a fundamental methodology for cognitive robots and machine learning. Traditional technologies for machine learning deal with object identification, cluster classification, pattern recognition, functional regression and behavior acquisition. A new category of CKL is presented in this paper embodied by the Algorithm of Cognitive Concept Elicitation (ACCE). Formal concepts are autonomously generated based on collective intension (attributes) and extension (objects) elicited from informal descriptions in dictionaries. A system of formal concept generation by cognitive robots is implemented based on the ACCE algorithm. Experiments on machine learning for knowledge acquisition reveal that a cognitive robot is able to learn synergized concepts in human knowledge in order to build its own knowledge base. The machine–generated knowledge base demonstrates that the ACCE algorithm can outperform human knowledge expressions in terms of relevance, accuracy, quantification and cohesiveness.
The taxonomy of machine learning can be classified into six categories including object identification, cluster classification, pattern recognition, functional regression, behavior acquisition (gaming) and knowledge learning (McCarthy et al., 1955; Chomsky, 1956; Simon, 1983; Zadeh, 1999; Mehryar et al., 2012; Wang, 2016b; Wang et al., 2017). The sixth category of Cognitive Knowledge Learning (CKL) is recently revealed (Wang, 2016a), which challenges traditional theories and methodologies for machine learning in artificial intelligence, cognitive robotics, cognitive computing and computational intelligence (Berkeley, 1954; Zadeh, 1983; Albus, 1991; Bender, 1996; Widrow & Lehr, 1990; Miller, 1995; Jordan, 1999; Meystel & Albus, 2002; Wang, 2002a, 2003, 2015b; Wang et al., 2006, 2016).
Fundamental problems for CKL are identified as lack of semantic theories, pending for suitable mathematical means, demand for formal models of knowledge representation and the support of a cognitive knowledge base. The problems are inherited in human knowledge expressions in natural languages due to subjection, diversity, redundancy, ambiguity, inexplicit semantics, incomplete intensions/extensions, mixed synonyms, and fuzzy concept relations (Miller, 1995; Zadeh, 1999; Mehryar et al., 2012; Wang, 2015c; Wang & Berwick, 2013). The problems also challenge traditional learning theories, machine cognition abilities, mathematical means for rigorous knowledge manipulations and machine semantical comprehension (Simon, 1983; Zadeh, 1983; Bender, 1996; Wang, 2008). Both fundamental theories and novel technologies are yet to be sought in order to gain breakthrough on the persistent problems of deep machine learning for knowledge acquisition.
The problems of machine learning in particular and AI challenges in general stem from the nature that they have been out of the traditional mathematical domain of real numbers and classical manipulations. It is recognized that the basic structural model of human knowledge is a formal concept (Wang, 2016a). Knowledge is acquired by a set of interacting cognitive processes such as object identification, concept elicitation, perception, inference, learning, comprehension, memorization, reasoning, analysis and synthesis (Wang et al., 2006). All cognitive processes are supported by a structural model of rigorous knowledge representation focusing on the attributes and objects of formal concepts as well as their relations (Wang, 2015a). Therefore, novel denotational mathematics (Wang, 2008, 2012) such as concept algebra (Wang, 2015a) and semantic algebra (Wang, 2013) are introduced to formally manipulate knowledge and semantics in CKL.
This paper elaborates a basic study on CKL by cognitive robots. It is presented by a novel algorithmic methodology and a set of experimental results for concept elicitation and generation by machine learning. In the remainder of this paper, Section 2 creates a set of mathematical models for formal knowledge representation and manipulation by concept algebra. Section 3 describes the algorithm of cognitive knowledge learning via formal concept generation. Section 4 demonstrates a set of machine-generated formal concepts obtained in the experiments according to the cognitive machine learning methodologies and the algorithm of cognitive concept elicitation.
2. MATHEMATICAL MODELS FOR COGNITIVE KNOWLEDGE LEARNING
The universe of discourse of knowledge as the context of concepts and semantics is a triple, i.e.,, encompassing finite and nonempty sets of objects , attributes and relations ℜ as a Cartesian product × (Wang, 2015a, 2016a).
Definition 1: A formal concept C in the universe of discourse of knowledge is a basic semantic structure of knowledge represented by a 5-tuple, i.e.:
(1)
where
Example 1: Let a pen be informally expressed as: “A pen is an instrument for writing with a nib and a container of ink such as a ballpoint, fountain and marker.” Then a formal concept, C1(pen), can be rigorously modeled for a cognitive robot according to Definition 1 as follows:
(2)
where the first attribute a* ∈ A1 denotes a hyponym or holonym that the concept belongs to, and is the current knowledge base represented by a set of formal concepts in .
In Example 1, the intension of the concept pen connotes the set of attributes of instrument, writing, nib and ink where instrument is a hypernym and the rest are hyponyms. The extension of pen denotes all potential objects (instances) of pens that share the common attributes as specified in the intension such as those of ballpoint, fountain and marker. The formal concept generated by CKL can be illustrated by the object-attribute-relation (OAR) model (Wang, 2007) as shown in Figure 1.
The semantic class of concept is noun, so are those of attribute and objects of a concept. Therefore, all attributes and objects can be uniformly described by the same denotational mathematical model of formal concepts according to Definition 1. Once there are exceptions in informal descriptions such as in the classes of adjectives, adverbs, verbs, and gerunds, they are transformed into equivalent nouns as conceptual synonyms.
| Figure 1. The OAR model of concept C1(pen) generated by machine learning |
|---|
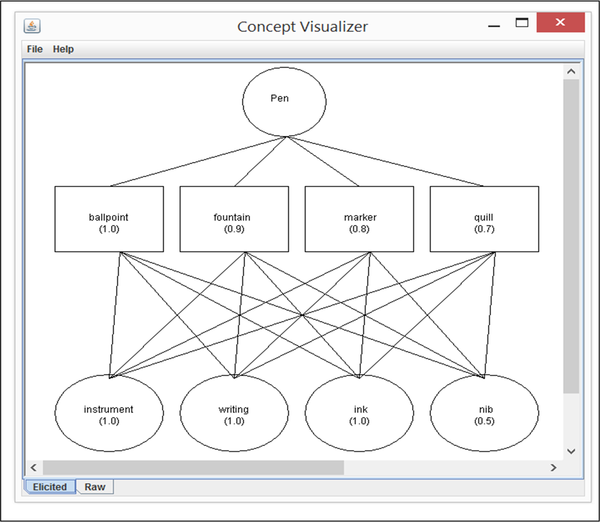 |
Definition 2: The structure model (SM) of a set of dictionaries, Dictionaries|SM, for machine learning is iteratively specified by the sets of informal attributes and objects, SynAttributes|S and SynObjects|S, preselected from sample dictionaries as a set of nouns and equivalent synonyms in other classes, i.e.:
(3)
where |SM, |N, |S and |Ξ are type suffices denoting those of structure models, natural number, string and set, respectively.
The big-R notation in Equation (3) and throughout this work, , is adopted from real-time process algebra (RTPA) (Wang, 2002b). Big-R is a generic iterative calculus for denoting and manipulating a finite nonempty set of recurring structures, sequential behaviors and/or conditionally repetitive behaviors.
Definition 3: The structure model of a formal concept, C+|SM, is a set of weighted attributes (AΣ|Ξ, wa|I) and objects (OΣ|Ξ, wo|I) collectively elicited from sample dictionaries, i.e.:
(4)
where wa|I and wo|I denote associate weights normalized in I = (0, 1) with respect to each attribute and object, respectively.
Definition 4: A synonym C’ to a given concept C in is a highly equivalent concept determined by their intensions embodied by the sets of attributes C.A and C’.A’, i.e.:
(5)
where θs is a given semantic threshold normally θs∈[0.9,1].
There are partial and contextual synonyms according to concept algebra. The former are partially equivalent with θs<0.9, while the latter are context-dependent concepts that are often transclass ones such as pairs of noun-pronouns, noun-adjective, noun-adverb and noun-gerund. When there exist multiple synonyms, a representative concept is selected among them. In the phase of supervised learning for formal concept elicitation, merges of equivalent synonyms are conducted by the machine with expert aids in the stage of this experiment. However, once the machine has built a comprehensive knowledge base with more than 1,000 formal concepts, unsupervised machine learning for autonomous concept generation and manipulations will be enabled.
Definition 5: The set of collective attributes of a machine generated concept C+, C+.AΣ, among n informal concepts D based on dictionary definitions is a weighted subset of commonly shared attributes from the set according to a given selection threshold θa, θa∈(0,1], i.e.:
(6)
Definition 6: The set of collective objects for a machine generated concept C+, C+.OΣ, among n informal concepts D based on dictionary definitions is a weighted subset of commonly shared objects from the set according to a given selection threshold θo, θo∈(0,1], i.e.:
(7)
In Definitions 4 through 6, the semantic thresholds of collective attributes θa|I, collective objects θo|I, and equivalence between synonyms θs|I are determined by needs in semantic analyses, which will be explained in Section 3.
It is noteworthy that attributes and objects are also concepts themselves at different layers of the knowledge hierarchy in . An attribute with respect to a certain concept is often a subconcept or hyponym of the given concept, while it can be a superconcept, hypernym or holonym at a higher layer where the given concept becomes a subconcept, hyponym or meronym, respectively. An object is an equivalent concept or synonym to the given concept. This semantic structure puts all formal concepts into a hierarchical framework of cognitive knowledge base according to concept algebra (Wang, 2015a).
3. ALGORITHM OF COGNITIVE KNOWLEDGE LEARNING BY COGNITIVE ROBOTS
On the basis of the mathematical models established in proceeding section, the Algorithm of Cognitive Knowledge Elicitation (ACCE) by machine learning is developed. The ACCE algorithm is formally described in Real Time Process Algebra (RTPA) (Wang, 2003b) as a rigorous process model (PM) as shown in Figure 2. The ACCE algorithm encompasses four phases for concept generation via those of preprocessing, attribute elicitation, object extraction and collective concept generation. The preprocessing phase of machine learning for formal concept generation is supervised with expert aids when the cognitive robot builds its knowledge base from scratch. Once there is a minimum critical mass of collective concepts in its knowledge base, the process of preprocessing will be fully implemented by unsupervised machine learning.
The structure models (SMs) of the ACCE algorithm encompass both formal concepts C+|SM and dictionaries Dictionaries|SM as defined in Equations (4) and (3). The inputs of the ACCE|PM algorithm consist of ten sample dictionaries Dictionaries|SM with preprocessed sets of attributes Dictionaries|SM.A|Ξ and Objects Dictionaries|SM.O|Ξ. The specific thresholds are used for tailoring the collective attributes (θa|I), collective objects (θo|I) and synonym equivalence (θs|I) in order to control the level of semantical equivalency. The outputs of ACCE|PM are a set of machine generated concepts C+|SM as formally modeled in Definition 3 with pairs of weighted collective attributes AΣ|Ξ(ai|S, wi|I) and collective objects OΣ|Ξ(oj|S, wj|I).
The ACCE algorithm elicits weighted candidate attributes from informal dictionary entries, eliminates redundant synonyms and determines weights of relevance for each selected attributes. It then extracts the set of collective objects in a similar process as that of collective attributes. Both subprocesses of ACCE create an initial concept that is refined in the third subprocess in order to generate the collective concept C+|SM tailored by a pair of expected thresholds for attributes θa|I and objects θo|I, respectively. Within the given range I = (0, 1), a stronger restriction on the semantic threshold will result in fewer links between synonyms and partial synonyms. Inversely, a relaxed semantic threshold will result in more potential conceptual relations between the set of formal concepts. Therefore, the former is suitable for deriving precise semantic relations in concept generation, while the latter is useful for detailed semantic analyses during machine learning. The machine learning results are maintained in a cognitive knowledge base (CKB) as a set of collective concepts, i.e., , in the global structure model (GM) of the algorithm as given in Figure 2.
4. EXPERIMENTAL RESULTS OF COGNITIVE MACHINE LEARNING
The ACCE algorithm as designed in Section 3 and described in Figure 2 is implemented in MATLAB (Zatarain & Wang, 2016). The experiments based on the ACCE algorithm identify 20 concepts in the categories of realistic entities, animals and abstract concepts as listed in Table 1. Ten dictionaries and related thesaurus are selected as sample entries in the experiments (Cambridge, 2016; Collins, 2016; Collins-T, 2016; DictCom, 2016; DictCom-T, 2016; Encyclopedia; 2016; Longman, 2016; MacMillan, 2016; MacMillan-T, 2016; OAED, 2016; OAEDS-S, 2016; OBED-B, 2016; Wang, 2016d; Webster, 2016; WordNet, 2016; WordRef, 2016; WordRef-T, 2016). The samples provide a set of 200 informal definitions of related words against the 20 target concepts. These informal words are transformed into formal concepts by CKL via the ACCE algorithm.
4.1. Formal Concepts Generated via Cognitive Machine Learning
The machine acquired knowledge with respect to the three categories of 20 concepts has been successfully generated by the ACCE algorithm as shown in Table 1. The experimental results are elicited from a 20 x 10 set of raw data based on varies informal definitions in natural languages among the sample dictionaries. Contrasting the machine learning result below and Example 1, the quantitative comprehension of the given concept by machine learning is well demonstrated.
| Figure 2. The ACCE algorithm for formal concept elicitation in RTPA |
|---|
 |
Table 1. Formal Concepts Generated by Machine Learning applying the ACCE Algorithm
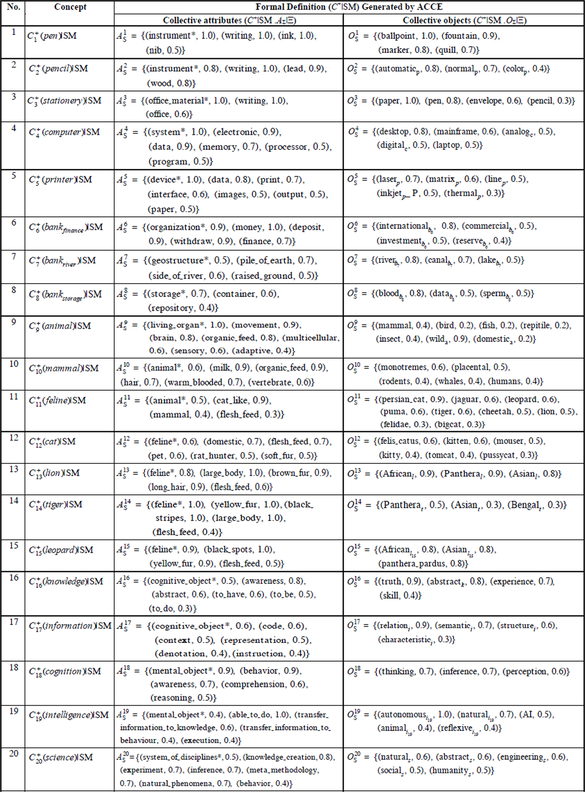 |
Example 2: The machine generated concept, , as obtained in the experiments as summarized in Table 1 as follows:
(8)
where the value associated to each attribute or object represents a weight of relevance evaluated by the ACCE algorithm according to Definitions 7 and 8, respectively.
Definition 7: The relative relevance of sample attributes, r(AS), elicited from a sample dictionary d is measured as a ratio of the size of common attributes shared by both sets of sample and collective attributes divided by the size of collective attributes |AΣ| learnt by machines, i.e.:
(9)
Definition 8: The relative relevance of sample objects, r(OS), elicited from a sample dictionary d is measured as a ratio of the size of common objects shared by both sets of sample and collective objects divided by the size of collective objects |OΣ| learnt by machines, i.e.:
(10)
The machine learning results obtained by the ACCE algorithm are both rigorous and quantitative. The weights of each attribute and object indicate basic properties of a formal concepts and the extent of their semantic relations. The formal concepts provide deep insight to characterize the semantic intension and extension via machine learning beyond human empirical perceptions in natural language comprehension and manipulations.
4.2. Analyses of the Experimental Results Generated by Machines
When the average weights of machine learning results in Table 1 are normalized to 1.0, the relative relevance of any informal concept sampled from dictionaries can be derived as shown in Tables 2 and 3 according to Equations (9) and (10), respectively. The average relevance of collective attributes and objects in the machine generated concepts are illustrated in Figure 3 based on data in Tables 2 and 3. Figure 3 shows that the relative accuracy of machine learnt results with respect to each sample concept is always beyond those of the average of sample dictionaries where the left- and right-hand-side subfigures show the comparative analyses between concept attributes and objects, respectively. Similar advantages on collective object learning are shown in Figure 4 based on the row averages in Tables 2 and 3 against each sample dictionaries. Both Figures 3 and 4 indicate that the relevance of collective attributes AΣ or objects OΣ generated by machine learning according to the ACCE algorithm are always beyond the average of sample dictionaries, because a dictionary may only represent a subset of empirical perceptions on the intension and extension of a certain concept.
It is recognized that natural language entries in dictionaries put emphases on the intension of a concept represented by the set of unquantified attributes. However, the extension of a concept denoted by the set of objects is often incomplete and without quantitative justification. There is also a tendency to mix the sets of attributes and objects particularly in online dictionaries which causes considerable level of semantic confusions. The experiments indicate that informal definitions of concepts in sample dictionaries are not work very well on abstract concepts such as those of science, information, knowledge, and intelligence. Therefore, the selection threshold needs to be fairly low in order to obtain sufficient collective attributes and objects for denoting the abstract concepts with expert refinement.
Table 2. Experimental Results of Collective Attributes Generated by Machines against Sample Dictionaries
| Dictionary (Di) |
Conceptual Relevance of Collective Attributes (rj(AS)) of Formal Concepts | Average relevance per dictionary ((Σrj(AS))/n) | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | C16 | C17 | C18 | C19 | C20 | ||
| D1 | 1.00 | 1.00 | 1.00 | 1.00 | 0.86 | 1.00 | 0.75 | 0.67 | 0.86 | 1.00 | 0.25 | 0.83 | 1.00 | 0.80 | 0.75 | 0.67 | 0.50 | 0.80 | 0.40 | 0.71 | 0.79 |
| D2 | 1.00 | 1.00 | 0.67 | 1.00 | 0.71 | 1.00 | 0.75 | 1.00 | 1.00 | 0.33 | 1.00 | 0.83 | 1.00 | 0.80 | 0.75 | 0.67 | 0.50 | 0.80 | 0.40 | 0.86 | 0.80 |
| D3 | 1.00 | 1.00 | 0.67 | 0.17 | 0.57 | 1.00 | 0.50 | 0.67 | 0.43 | 0.83 | 0.25 | 0.50 | 1.00 | 0.80 | 0.75 | 0.67 | 0.67 | 0.60 | 0.20 | 0.29 | 0.63 |
| D4 | 1.00 | 0.50 | 1.00 | 1.00 | 0.71 | 1.00 | 0.50 | 0.33 | 0.86 | 0.67 | 0.50 | 0.67 | 0.80 | 1.00 | 1.00 | 0.67 | 0.33 | 0.60 | 0.40 | 0.71 | 0.71 |
| D5 | 1.00 | 0.75 | 0.67 | 0.50 | 0.71 | 0.80 | 0.50 | 0.67 | 1.00 | 0.83 | 0.50 | 0.33 | 1.00 | 1.00 | 1.00 | 0.67 | 0.83 | 0.40 | 1.00 | 0.86 | 0.75 |
| D6 | 0.75 | 0.75 | 0.67 | 0.67 | 0.43 | 0.60 | 0.50 | 0.00 | 0.71 | 0.67 | 0.25 | 0.83 | 0.80 | 1.00 | 0.75 | 0.83 | 0.83 | 0.60 | 0.40 | 0.57 | 0.63 |
| D7 | 0.75 | 1.00 | 0.67 | 1.00 | 0.57 | 1.00 | 0.75 | 0.67 | 0.71 | 0.50 | 0.25 | 0.50 | 0.60 | 0.80 | 0.50 | 0.33 | 0.17 | 0.80 | 1.00 | 1.00 | 0.68 |
| D8 | 0.75 | 0.75 | 1.00 | 0.67 | 0.86 | 1.00 | 0.75 | 0.33 | 0.71 | 1.00 | 0.50 | 0.67 | 0.80 | 1.00 | 1.00 | 0.33 | 0.83 | 1.00 | 1.00 | 0.57 | 0.78 |
| D9 | 0.75 | 1.00 | 0.67 | 0.67 | 0.57 | 0.60 | 0.50 | 1.00 | 0.29 | 0.67 | 0.75 | 0.17 | 0.40 | 0.80 | 0.75 | 0.17 | 0.17 | 0.60 | 0.40 | 0.57 | 0.57 |
| D10 | 0.75 | 1.00 | 1.00 | 0.83 | 0.57 | 0.80 | 0.25 | 0.33 | 0.71 | 0.50 | 1.00 | 0.50 | 1.00 | 0.80 | 1.00 | 0.50 | 0.33 | 0.60 | 0.40 | 0.57 | 0.67 |
| Average relevance per concept ((Σri(AS))/n) |
0.88 | 0.88 | 0.80 | 0.75 | 0.66 | 0.88 | 0.58 | 0.57 | 0.73 | 0.70 | 0.53 | 0.58 | 0.84 | 0.88 | 0.83 | 0.55 | 0.52 | 0.68 | 0.56 | 0.67 | |
Table 3. Experimental Results of Collective Objects Generated by Machines against Sample Dictionaries
| Dictionary (Di) |
Conceptual Relevance of Collective Objects (rj(OS)) of Formal Concepts | Average relevance per dictionary ((Σrj(OS))/n) | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | C16 | C17 | C18 | C19 | C20 | ||
| D1 | 0.75 | 1.00 | 0.75 | 0.60 | 0.00 | 0.75 | 1.00 | 0.67 | 0.14 | 1.00 | 0.10 | 0.67 | 1.00 | 0.67 | 0.67 | 0.75 | 0.50 | 1.00 | 1.00 | 0.40 | 0.67 |
| D2 | 0.75 | 0.33 | 0.75 | 0.40 | 0.00 | 0.75 | 1.00 | 0.67 | 0.14 | 1.00 | 0.90 | 0.50 | 1.00 | 0.67 | 1.00 | 0.75 | 1.00 | 1.00 | 0.40 | 0.40 | 0.67 |
| D3 | 1.00 | 0.33 | 0.25 | 0.80 | 0.20 | 1.00 | 0.67 | 0.33 | 0.57 | 0.40 | 0.30 | 0.17 | 0.33 | 0.67 | 0.33 | 0.75 | 0.50 | 0.67 | 0.60 | 1.00 | 0.54 |
| D4 | 1.00 | 0.67 | 0.50 | 0.60 | 0.60 | 0.75 | 1.00 | 0.67 | 0.29 | 1.00 | 0.20 | 0.17 | 1.00 | 0.33 | 1.00 | 0.50 | 0.75 | 0.33 | 0.60 | 0.20 | 0.61 |
| D5 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 0.14 | 0.00 | 0.00 | 0.67 | 1.00 | 0.33 | 1.00 | 1.00 | 0.75 | 0.33 | 0.80 | 0.60 | 0.68 |
| D6 | 0.75 | 0.67 | 0.50 | 0.60 | 0.80 | 0.25 | 0.33 | 0.00 | 0.43 | 0.40 | 0.80 | 1.00 | 1.00 | 0.67 | 1.00 | 0.75 | 0.75 | 0.33 | 0.20 | 0.00 | 0.56 |
| D7 | 1.00 | 0.67 | 1.00 | 0.60 | 0.80 | 0.75 | 1.00 | 0.67 | 0.71 | 0.20 | 0.70 | 0.17 | 0.33 | 0.00 | 0.67 | 0.75 | 0.50 | 1.00 | 0.60 | 0.80 | 0.65 |
| D8 | 1.00 | 0.67 | 0.75 | 1.00 | 0.80 | 0.25 | 0.67 | 1.00 | 0.86 | 0.00 | 0.80 | 1.00 | 1.00 | 0.67 | 1.00 | 0.50 | 0.75 | 1.00 | 0.60 | 1.00 | 0.77 |
| D9 | 0.75 | 0.33 | 0.50 | 0.00 | 0.20 | 0.00 | 0.33 | 0.33 | 0.14 | 0.60 | 0.90 | 0.17 | 1.00 | 0.33 | 0.33 | 0.50 | 0.25 | 0.00 | 1.00 | 0.40 | 0.40 |
| D10 | 0.50 | 0.67 | 0.75 | 0.20 | 0.80 | 1.00 | 0.33 | 0.67 | 0.00 | 0.00 | 0.80 | 0.17 | 1.00 | 0.33 | 1.00 | 0.75 | 0.50 | 0.33 | 0.20 | 0.80 | 0.54 |
| Average relevance per concept ((Σri(OS))/n) |
0.85 | 0.63 | 0.68 | 0.58 | 0.52 | 0.55 | 0.73 | 0.60 | 0.34 | 0.46 | 0.55 | 0.47 | 0.87 | 0.47 | 0.80 | 0.70 | 0.63 | 0.60 | 0.60 | 0.56 | |
| Figure 3. Semantic accuracy between machine learnt results and the average of sample concepts |
|---|
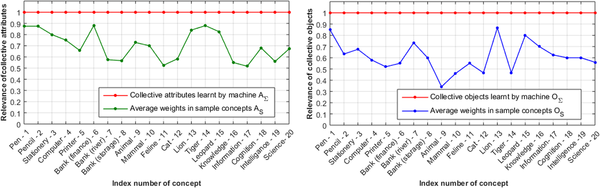 |
| Figure 4. Semantic accuracy between machine learnt results and the average of sample dictionaries |
|---|
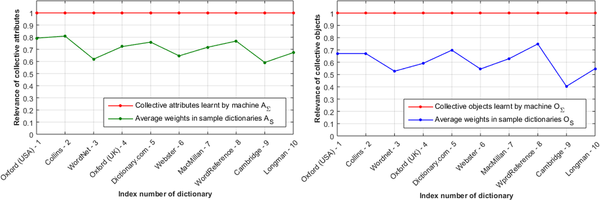 |
It is revealed in concept algebra that both sets of attributes and objects uniquely constitute the intension and extension of a formal concepts, which form the basic structural unit of human and machine knowledge. The experimental results demonstrate that few dictionaries or human learners may accurately and quantitatively define a formal concept due to the subjectivity of individuals, constraints of natural languages and the complexity of semantic quantification. These are the reasons of fuzziness underpinning the fundamental structure of human knowledge, which may be significantly improved by machines learning in cognitive linguistics. The experimental results indicate that machine-generated concepts via CKL can generally outperform humans towards formal representation and cognition of common knowledge by cognitive robots supported by the ACCE algorithm and powered by concept algebra.
It has been recognized that Cognitive Knowledge Learning (CKL) by cognitive robots is a fundamental theoretical problem and technical challenge in machine learning and computational intelligence. Supported by concept algebra and a cognitive knowledge base, the Algorithm of Cognitive Concept Elicitation (ACCE) for deep machine learning has been presented. A set of 200 experiments has reported on 20 machine-generated concepts autonomous elicited from ten sample dictionaries. This work has demonstrated that cognitive robots are able to outperform humans in knowledge acquisition and formal concept learning. It has paved a way towards a rigorous machine knowledge learning theory and novel technologies enabling applications in machine-generated knowledge bases sharable by both man and cognitive robots.
This research was previously published in the International Journal of Cognitive Informatics and Natural Intelligence (IJCINI), 11(3); edited by Kangshun Li; pages 31-46, copyright year 2017 by IGI Publishing (an imprint of IGI Global).
The authors would like to acknowledge the support in part by a Discovery Grant of the Natural Sciences and Engineering Research Council of Canada (NSERC). Omar Zatarain acknowledges the support of the PRODEP program sponsored by the Secretariat of Public Education, Government of Mexico. The authors would like to thank the anonymous reviewers for their valuable suggestions and comments.
Albus, J. (1991). Outline for a Theory of Intelligence . IEEE Transactions on Systems, Man, and Cybernetics , 21(3), 473–509. doi:10.1109/21.97471
Bender, E. A. (1996). Mathematical Methods in Artificial Intelligence . Los Alamitos, CA: IEEE CS Press.
Berkeley, B. (1954). Principles of Human Knowledge (A.D. Lindsay ed.). (originally published 1710)
Cambridge English Online Dictionary. (2016). Cambridge University Press.
Chomsky, N. (1956). Three Models for the Description of Languages . I.R.E. Transactions on Information Theory , IT-2(3), 113–124. doi:10.1109/TIT.1956.1056813
Collins. (2016). Collins Thesaurus. Retrieved from http://www.collinsdictionary.com/english-thesaurus
Collins. (2016). Collins Online Dictionary. Retrieved from http://www.collinsdictionary.com/dictionary/english/
DictCom. (2016). Dictionary.com. Retrieved from http://dictionary.reference.com/
DictCom-T. (2016). Thesaurus.com. Retrieved from http://www.thesaurus.com/
Encyclopedia.com. (2016). Encyclopedia. Retrieved from http://www.encyclopedia.com/
Jordan, M.I., & Russell, S. (1999). Computational Intelligence. In R.A. Wilson & C.K. Frank (Eds.), The MIT Encyclopedia of the Cognitive Sciences (pp. i.73-80). MIT Press.
Longman. (2016). Longman English Online Dictionary. Retrieved from http://www.ldoceonline.com/
MacMillan. (2016). Macmillan British Online Dictionary.
MacMillan. (2016). Online Thesaurus of Macmillan Dictionary.
McCarthy, J., Minsky, M. L., Rochester, N., & Shannon, C. E. (1955). Proposal for the 1956 Dartmouth Summer Research Project on Artificial Intelligence. Dartmouth College, Hanover, NH.
Mehryar, M., Rostamizadeh, A., & Talwalkar, A. (2012). Foundations of machine learning . MIT press.
Meystel, A. M., & Albus, J. S. (2002). Intelligent Systems, Architecture, Design, and Control . John Wiley & Sons, Inc.
Miller, G. A. (1995). WordNet: A Lexical Database for English . Communications of the ACM , 38(11), 39–41. doi:10.1145/219717.219748
OAED. (2016). Oxford Online Dictionary of English.
OAEDS-S. (2016). Oxford Online Synonyms of English.
OBED-B. (2016). Oxford British English Dictionary .
Simon, H.A. (1983). Why Should Machines Learn? In R.S. Michalskl et al. (Eds.), Machine Learning, an Artificial approach (pp. 25-35). Tioga Publishing Co.
SynCom. (2016), http://www.synonym.com/synonyms/online
Wang, Y. (2002a). Keynote: On Cognitive Informatics. In Proceedings of the 1st IEEE International Conference on Cognitive Informatics (ICCI’02), Calgary, Canada (pp. 34-42). IEEE CS Press. 10.1109/COGINF.2002.1039280
Wang, Y. (2002b). The Real-Time Process Algebra (RTPA) . Annals of Software Engineering, Springer , 14(1/4), 235–274. doi:10.1023/A:1020561826073
Wang, Y. (2003), On Cognitive Informatics. Brain and Mind: A Transdisciplinary Journal of Neuroscience and Neurophilosophy, 4(2), 151-167.
Wang, Y. (2007). The OAR Model of Neural Informatics for Internal Knowledge Representation in the Brain . International Journal of Cognitive Informatics and Natural Intelligence , 1(3), 66–77. doi:10.4018/jcini.2007070105
Wang, Y. (2008). On Contemporary Denotational Mathematics for Computational Intelligence . Transactions of Computational Science, 2, 6–29. doi:10.1007/978-3-540-87563-5_2
Wang, Y. (2012). In Search of Denotational Mathematics: Novel Mathematical Means for Contemporary Intelligence, Brain, and Knowledge Sciences . Journal of Advanced Mathematics and Applications , 1(1), 4–25. doi:10.1166/jama.2012.1002
Wang, Y. (2013). On Semantic Algebra: A Denotational Mathematics for Natural Language Comprehension and Cognitive Computing . Journal of Advanced Mathematics and Applications , 2(2), 145–161. doi:10.1166/jama.2013.1039
Wang, Y. (2015a). Concept Algebra: A Denotational Mathematics for Formal Knowledge Representation and Cognitive Robot Learning . Journal of Advanced Mathematics and Applications , 4(1), 1–26. doi:10.1166/jama.2015.1066
Wang, Y. (2015b). Formal Cognitive Models of Data, Information, Knowledge, and Intelligence . WSEAS Trans. Computers , 14, 770–781.
Wang, Y. (2015c). Cognitive Learning Methodologies for Brain-Inspired Cognitive Robotics . International Journal of Cognitive Informatics and Natural Intelligence , 9(2), 37–54. doi:10.4018/IJCINI.2015040103
Wang, Y. (2016a). On Cognitive Foundations and Mathematical Theories of Knowledge Science . International Journal of Cognitive Informatics and Natural Intelligence , 10(2), 1–24. doi:10.4018/IJCINI.2016040101
Wang, Y. (2016b, August 22-23). Keynote: Deep Reasoning and Thinking beyond Deep Learning by Cognitive Robots and Brain-Inspired Systems. In Proceedings of 15th IEEE International Conference on Cognitive Informatics and Cognitive Computing (ICCI*CC 2016), Stanford University, Stanford, CA. IEEE CS Press.
Wang, Y. (2016c). Keynote: Cognitive Soft Computing: Philosophical, Mathematical, and Theoretical Foundations of Cognitive Robotics. In Proceedings of 6th World Conference on Soft Computing (WConSC 2016), UC Berkeley, CA. Springer.
Wang, Y. (2016d). Big Data Algebra (BDA): A Denotational Mathematics for Big Data Science and Engineering . Journal of Advanced Mathematics and Applications , 5(1), 1–23.
Wang, Y. (in press), Building Cognitive Knowledge Bases Sharable by Humans and Cognitive Robots. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (IEEE SMC’17), Banff, Canada.
Wang, Y., & Berwick, R. C. (2013). Formal Relational Rules of English Syntax for Cognitive Linguistics, Machine Learning, and Cognitive Computing . Journal of Advanced Mathematics and Applications , 2(2), 182–195. doi:10.1166/jama.2013.1042
Wang, Y., Wang, Y., Patel, S., & Patel, D. (2006). A Layered Reference Model of the Brain (LRMB). IEEE Trans. Syst., Man, and Cybernetics Part C , 36(2), 124–133.
Wang, Y., Widrow, B., Zadeh, L. A., Howard, N., Wood, S., Bhavsar, V. C., & Shell, D. F. (2016). Cognitive Intelligence: Deep Learning, Thinking, and Reasoning with Brain-Inspired Systems . International Journal of Cognitive Informatics and Natural Intelligence , 10(4), 1–21. doi:10.4018/IJCINI.2016100101
Wang, Y. L. A., Zadeh, L. A., Widrow, B., Howard, N., Beaufays, F., Baciu, G., & Zhang, D. (2017, January). Abstract Intelligence: Embodying and Enabling Cognitive Systems by Mathematical Engineering . International Journal of Cognitive Informatics and Natural Intelligence , 11(1), 1–15. doi:10.4018/IJCINI.2017010101
Webster. (2016). Webster Online Dictionary and Thesaurus. Retrieved from http://www.merriam-webster.com/dictionary/
WidrowB.LehrM. A. (1990), 30 Years of Adaptive Neural Networks: Perception, Madeline, and Backpropagation. Proc. of the IEEE, 78(9), 1415-1442. 10.1109/5.58323
WordNet. (2016), WordNet 3.0. Retrieved from http://wordnetweb.princeton.edu/perl/webwn
WordRef. (2016). Wordreference.com Online Dictionary of American English . Random House.
WordRef-T. (2016). WordReference.com English Thesaurus. Retrieved from http://www.wordreference.com/synonyms
Zadeh, L. A. (1983). A Computational Approach to Fuzzy Quantifiers in Natural Languages . Computers & Mathematics with Applications (Oxford, England) , 9(1), 149–184. doi:10.1016/0898-1221(83)90013-5
Zadeh, L. A. (1999). From Computing with Numbers to Computing with Words: From Manipulation of Measurements to Manipulation of Perceptions . IEEE Transactions on Circuits and Systems , 45(1), 1–2.
Zatarain, O. A., & Wang, Y. (2016). Experiments on the Supervised Learning Algorithm for Formal Concept Elicitation by Cognitive Robots. In Proceedings of 15th IEEE International Conference on Cognitive Informatics and Cognitive Computing (ICCI*CC 2016), Stanford University, CA (pp. 86-96). IEEE CS Press. 10.1109/ICCI-CC.2016.7862015