© Springer Nature Switzerland AG 2020
P. Cellier, K. Driessens (eds.)Machine Learning and Knowledge Discovery in DatabasesCommunications in Computer and Information Science1168https://doi.org/10.1007/978-3-030-43887-6_2

Modeling Evolving User Behavior via Sequential Clustering

Veselka Boeva1   and Christian Nordahl1  
(1)
Blekinge Institute of Technology, 371 79 Karlskrona, Sweden
 
 
Veselka Boeva (Corresponding author)
Email: veselka.boeva@bth.se
 
Christian Nordahl
Email: christian.nordahl@bth.se

Abstract

In this paper we address the problem of modeling the evolution of clusters over time by applying sequential clustering. We propose a sequential partitioning algorithm that can be applied for grouping distinct snapshots of streaming data so that a clustering model is built on each data snapshot. The algorithm is initialized by a clustering solution built on available historical data. Then a new clustering solution is generated on each data snapshot by applying a partitioning algorithm seeded with the centroids of the clustering model obtained at the previous time interval. At each step the algorithm also conducts model adapting operations in order to reflect the evolution in the clustering structure. In that way, it enables to deal with both incremental and dynamic aspects of modeling evolving behavior problems. In addition, the proposed approach is able to trace back evolution through the detection of clusters’ transitions, such as splits and merges. We have illustrated and initially evaluated our ideas on household electricity consumption data. The results have shown that the proposed sequential clustering algorithm is robust to modeling evolving behavior by being enable to mine changes and update the model, respectively.

Keywords
Behavior modelingClustering evolutionData miningSequential clusteringHousehold electricity consumption data

1 Introduction

The need for describing and understanding the behavior of a given phenomenon over time led to the emergence of new techniques and methods focused in temporal evolution of data and models [2, 6, 13]. Data mining techniques and methods that enable to monitor models and patterns over time, compare them, detect and describe changes, and quantify them on their interestingness are encompassed by the paradigm of change mining [5]. The two main challenges of this paradigm are to be able to adapt models to changes in data distribution but also to analyze and understand changes themselves.

Evolving clustering models are referred to incremental or dynamic clustering methods, because they can process data step-wise and update and evolve cluster partitions in incremental learning steps [6, 10]. Incremental (sequential) clustering methods process one data element at a time and maintain a good solution by either adding each new element to an existing cluster or placing it in a new singleton cluster while two existing clusters are merged into one [1, 7, 17]. Dynamic clustering is also a form of online/incremental unsupervised learning. However, it considers not only incrementality of the methods to build the clustering model, but also self-adaptation of the built model. In that way, incrementality deals with the problem of model re-training over time and memory constrains, while dynamic aspects (e.g., data behavior, clustering structure) of the model to be learned can be captured via adaptation of the current model. Lughofer proposes an interesting dynamic clustering algorithm which is also dedicated to incremental clustering of data streams and in addition, it is equipped with dynamic split-and-merge operations [10]. A similar approach defining a set of splitting and merging action conditions is introduced in [8]. Wang et al. also propose a split-merge-evolve algorithm for clustering data into k number of clusters [16]. However, a k cluster output is always provided by the algorithm, i.e. it is not sensitive to the evolution of the data. A split-merge evolutionary clustering algorithm which is robust to evolving scenarios is introduced in [4]. The algorithm is designed to update the existing clustering solutions based on the data characteristics of newly arriving data by either splitting or merging existing clusters. Notice that all these algorithms have the ability to optimize the clustering result in scenarios where new data samples may be added in to existing clusters.

In this paper, we propose a sequential (dynamic) partitioning algorithm that is robust to modeling the evolution of clusters over time. In comparison with the above discussed dynamic clustering algorithms it does not update existing clustering, but groups distinct portions (snapshot) of streaming data so that a clustering model is generated on each data portion. The algorithm initially produces a clustering solution on available historical data. A clustering model is generated on each new data snapshot by applying a partitioning algorithm initialized with the centroids of the clustering solution built on the previous data snapshot. In addition, model adapting operations are performed at each step of the algorithm in order to capture the clusters’ evolution. Hence, it tackles both incremental and dynamic aspects of modeling evolving behavior problems. The algorithm also enables to trace back evolution through the identification of clusters’ transitions such as splits and merges. We have studied and initially evaluated our algorithm on household electricity consumption data. The results have shown that it is robust to modeling evolving data behavior.

2 Modeling Evolving User Behavior via Sequential Clustering

2.1 Sequential Partitioning Algorithm

In this section, we formally describe the proposed sequential partitioning algorithm. The algorithm idea is schematically illustrated in Fig. 1.

Assume that data sets $$D_0, D_1,\ldots , D_n$$ are distinct snapshots of a data stream. Further let $$C = \{C_i | i = 0, 1,\ldots ,n\}$$ be a set of clustering solutions (models), such that $$C_i$$ has been built on a data set $$D_i$$. In addition, each clustering solution $$C_i$$, for $$i= 1, 2,\ldots , n$$, is generated by applying a partitioning algorithm (see Sect. 2.2) on data set $$D_i$$ initialized (seeded) with the centroids of the clustering model built on data set $$D_{i-1}$$. The algorithm is initialized by clustering $$C_0$$ which is extracted from data set $$D_0$$ (available historical data or the initial snapshot).
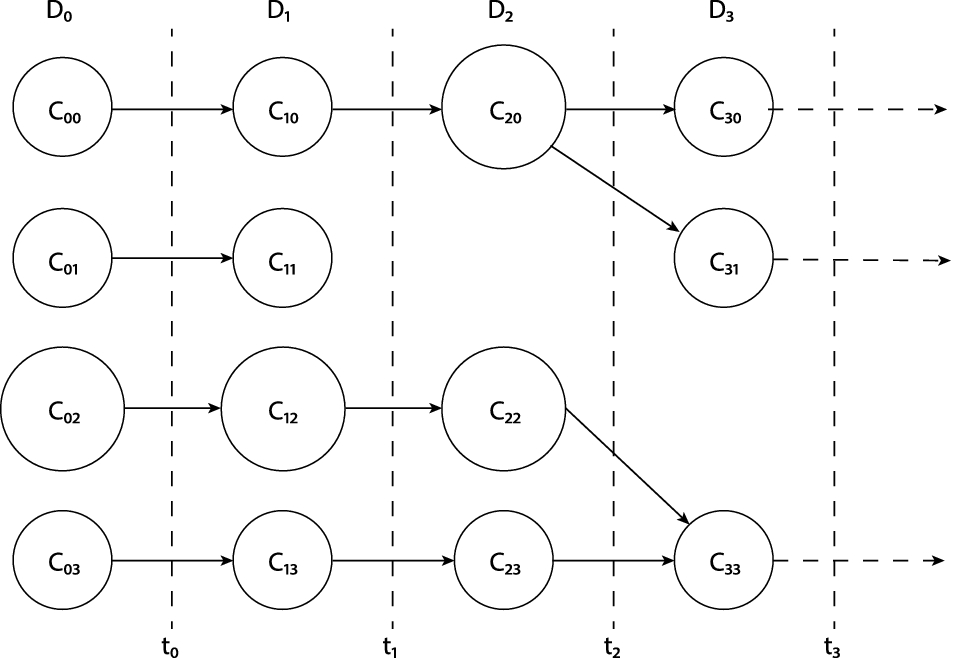
../images/496776_1_En_2_Chapter/496776_1_En_2_Fig1_HTML.png
Fig. 1.

Schematic illustration of the proposed sequential clustering approach

The basic operations conducted by our algorithm at each time window (on each data snapshot) i are explained below:
  1. 1.

    Input: Cluster centroids of partition $$C_{i-1}$$ ($$i=1, 2,\ldots , n$$).

     
  2. 2.

    Clustering step: Cluster data set $$D_i$$ by seeding the partitioning algorithm with the centroids of $$C_{i-1}$$.

    1. (a)

      Initial clustering of $$D_i$$.

       
    2. (b)

      Check for empty initial clusters and adapt the partitioning respectively.

       
    3. (c)

      Remove the seeded centroids and finalize the clustering by producing $$C_i$$.

       
     
  3. 3.
    Adapting step: For each cluster $$C_{ij}\in C_i$$ do the following steps
    1. (a)

      Calculate the split condition for $$C_{ij}$$.

       
    2. (b)

      If the split condition is satisfied then split $$C_{ij}$$ into two clusters by applying 2-medoids clustering algorithm and update the list of centroids, respectively.

       
     
  4. 4.

    Output: Updated clustering partition and list of centroids used to initialize the clustering action that will be conducted on data set $$D_{i+1}$$.

     

Note that at step 2(b) above we check whether there are empty clusters after the initial clustering. If so, this means that the clustering structure is evolving, i.e. some clusters may stop existing while others are merged together. Evidently, the death and merge transitions are part of the clustering step. Therefore the split condition is only checked at step 31. We can apply different split conditions. For example, the homogeneity of each cluster $$C_{ij}$$ may be evaluated and if it is below a given threshold we will perform splitting. Another possibility is to apply the idea implemented by Lughofer [10] in his dynamic split-and-merge algorithm.

In order to trace back the clusters’ evolution we can compare the sets of cluster centroids of each pair of partitioning solutions extracted from the corresponding neighboring time intervals (e.g., see Fig. 6). This comparison can be performed by applying some alignment technique, e.g., such as Dynamic Time Warping (DTW) algorithm explained in Sect. 2.3. For example, if we consider two consecutive clustering solutions $$C_{i-1}$$ and $$C_i$$ ($$i=1, 2,\ldots , n$$), we can easily recognize two scenarios: (i) a centroid of $$C_{i-1}$$ is aligned to two or more centroids of $$C_i$$ then the corresponding cluster from $$C_{i-1}$$ splits among the aligned ones from $$C_i$$; (ii) a few centroids of $$C_{i-1}$$ is aligned to a centroid of $$C_i$$ then the corresponding clusters from $$C_{i-1}$$ merge into the aligned cluster from $$C_i$$.

2.2 Partitioning Algorithms

Three partitioning algorithms are commonly used for data analysis to divide the data objects into k disjoint clusters [11]: k-means, k-medians, and k-medoids clustering. The three partitioning methods differ in how the cluster center is defined. In k-means clustering, the cluster center is defined as the mean data vector averaged over all objects in the cluster. In k-medians, the median is calculated for each dimension in the data vector to create the centroid. Finally, in k-medoids clustering, which is a robust version of the k-means, the cluster center is defined as the object with the smallest sum of distances to all other objects in the cluster, i.e., the most centrally located point in a given cluster.
../images/496776_1_En_2_Chapter/496776_1_En_2_Fig2_HTML.png
Fig. 2.

Initial clustering model produced on the historical data.

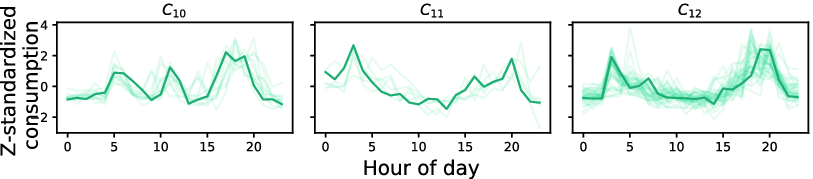
../images/496776_1_En_2_Chapter/496776_1_En_2_Fig3_HTML.png
Fig. 3.

Clustering model produced on the first new data snapshot. Clusters $$C_{01}$$ and $$C_{03}$$ have been empty after the clustering step. Clusters $$C_{02}$$ and $$C_{04}$$ are transformed in clusters $$C_{11}$$ and $$C_{12}$$, respectively.

2.3 Dynamic Time Warping Algorithm

The DTW alignment algorithm aims at aligning two sequences of feature vectors by warping the time axis iteratively until an optimal match (according to a suitable metrics) between the two sequences is found [15]. Let us consider two matrices $$A = [a_1,\ldots , a_n]$$ and $$B = [b_1,\ldots , b_m]$$ with $$a_i$$ ($$i=1,\ldots ,n$$) and $$b_j$$ ($$j=1,\ldots ,m$$) column vectors of the same dimension. The two vector sequences $$[a_1,\ldots , a_n]$$ and $$[b_1,\ldots , b_m]$$ can be aligned against each other by arranging them on the sides of a grid, e.g., one on the top and the other on the left hand side. A distance measure, comparing the corresponding elements of the two sequences, can then be placed inside each cell. To find the best match or alignment between these two sequences one needs to find a path through the grid $$P=(1,1),\ldots ,(i_s,j_s),\ldots ,(n,m)$$, ($$1\le i_s\le n$$ and $$1\le j_s\le m$$), which minimizes the total distance between A and B.

3 Case Study: Modeling Household Electricity Consumption Behavior

3.1 Case Description

Suppose that a monitoring system for tracking changes in electricity consumption behavior at a household level is developed to be used for some healthcare application. For example, such a system can be used to monitor and look for alterations in the daily routines (sleep-wake cycle) of elderly individuals who have been diagnosed with a neurodegenerative disease. The system is supposed to build and maintain an electricity consumption behavior model for each monitored household. Initially, a model of normal electricity consumption behavior is created for each particular household by using historical data [12]. In order to monitor such a model over time it is necessary to build a new model on each new portion of electricity consumption data and then compare the current model with the new household electricity consumption behavior model. If changes are identified a further analysis of the current electricity consumption behavior model is performed in order to investigate whether these are associated with alterations in the resident’s daily routines.
../images/496776_1_En_2_Chapter/496776_1_En_2_Fig4_HTML.png
Fig. 4.

Clustering models produced on the second (above) and third (below) new data snapshots, respectively.

3.2 Data and Experiments

We use electricity consumption data collected from a single randomly selected anonymous household that has been collected with a 1-min interval for a period of 14 months. During those 14 months, there were roughly 2 months worth of data that had not been collected, i.e. zero values which have been removed. We then aggregate the electricity consumption data into a one hour resolution from the one minute resolution.

We divide the data into four parts. The first 50% of the total data represent the historical data ($$D_0$$), and the remaining data is evenly distributed into the other three data sets ($$D_1$$, $$D_2$$ and $$D_3$$). In addition, $$D_2$$ and $$D_3$$ have their contents shifted to simulate a change in their behavior over time. 8% of the contents in $$D_2$$ is randomly shifted 1 to 6 h ahead, and 2% of the contents 12 h ahead. Similarly, $$D_3$$ has 16% of the data shifted 1 to 6 h ahead and 4% 12 h ahead. We choose these two scenarios to simulate both minor and drastic changes in the sleeping pattern of the resident.

In order to cluster the historical data, we run k-medoids 100 times using randomly initialized cluster medoids, for each k between 2 and 20. DTW is used as the dissimilarity measure and it is restricted to only allow for a maximum warp of two hours. This restriction is in place to allow for some minor alterations in the daily behavior while keeping major alterations in check. The produced clustering solutions are then evaluated using Silhouette Index [14], Connectivity [9], and Average Intra-Cluster distance [3]. The medoids from the best scoring clustering solution are then used as the initial seeds for the next snapshot of data, as explained in Sect. 2.1.
Table 1.

Distances between the clustering models generated on the first and second new data snapshots (left), and on the second and third new data snapshots (right), respectively.

../images/496776_1_En_2_Chapter/496776_1_En_2_Tab1_HTML.png

3.3 Results and Discussion

Figure 2 shows the initial clustering model generated on the historical data. As one can see the household electricity consumption behavior is modeled by five different behavior profiles (clusters). $$C_{03}$$ and $$C_{04}$$ are the biggest clusters and represent the electricity consumption behavior more typical for working days with clearly recognized morning and evening consumption peaks. Clusters $$C_{00}$$ and $$C_{01}$$ are smaller and have an additional consumption peak in the middle of the day, i.e. they model behavior more typical for the weekends. Cluster $$C_{02}$$ is comparatively big and represents electricity consumption behavior typical for working days with a slightly later start.
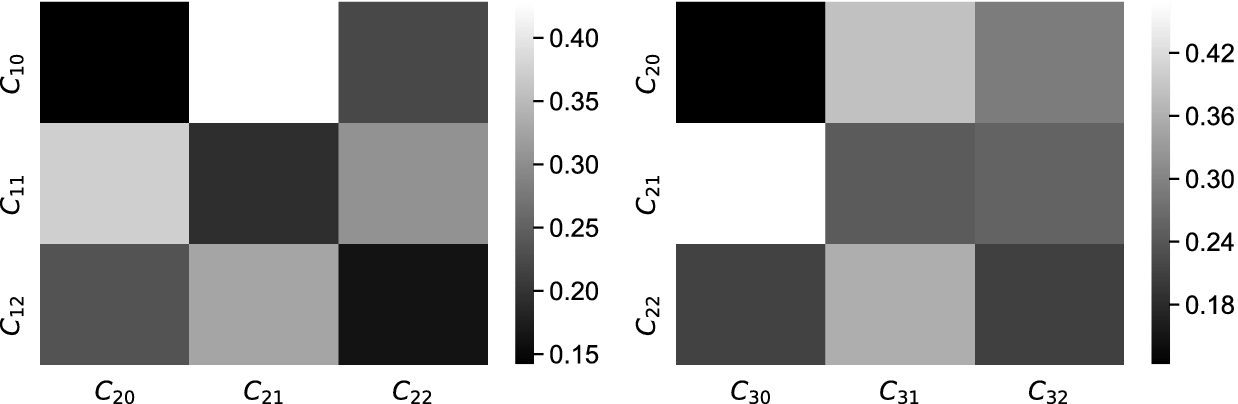
../images/496776_1_En_2_Chapter/496776_1_En_2_Fig5_HTML.png
Fig. 5.

Heatmaps for distances between the clustering models generated on the first and second new data snapshots (left), and on the second and third new data snapshots (right), respectively.

Figure 3 depicts the clustering model derived from the first new data snapshot. As we can notice the electricity consumption behavior is modeled only by three clusters. $$C_{01}$$ and $$C_{03}$$ have been empty after the initial clustering step and their medoids are removed from the list of medoids. Clusters $$C_{02}$$ and $$C_{04}$$ are transformed into clusters $$C_{11}$$ and $$C_{12}$$, respectively. It is interesting to observe that $$C_{12}$$ is also very similar to cluster profile $$C_{03}$$. The latter observation is also supported by the DTW alignment between the medoids of the two clustering models given in Fig. 6, where $$C_{03}$$ and $$C_{04}$$ are aligned to $$C_{12}$$, i.e. they are merged into one cluster. This is also the case for $$C_{00}$$ and $$C_{01}$$, which are replaced by cluster $$C_{10}$$ at the first time interval.

As it can be seen in Fig. 4 the number of clusters is not changed at the second and third time windows. However, one can easily observe that behavior profile $$C_{11}$$ evolves its shape over these two time intervals. For example, it moves far from $$C_{21}$$ and gets closer to $$C_{20}$$ at the third time window (see Table 1). These observations are also supported by the heatmaps plotted in Fig. 5. One can observe that the respective cells in the heatmap plotted in Fig. 5 (right) have changed their color in comparison with the heatmap in Fig. 5 (left).
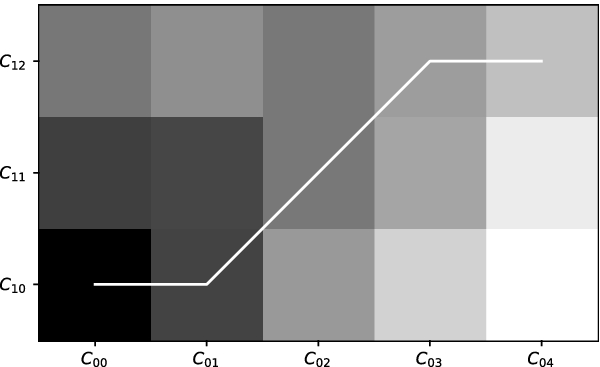
../images/496776_1_En_2_Chapter/496776_1_En_2_Fig6_HTML.png
Fig. 6.

DTW alignment path between the clustering models generated on the historical and first new snapshot data, respectively.

We can trace the evolution of the clusters at each step of our algorithm by comparing the sets of cluster centroids of each pair of clusterings extracted from the corresponding consecutive time intervals. This is demonstrated in Fig. 6 which plots the DTW alignment path between the clustering models generated on the historical and first new data sets, respectively. This comparison can be performed on any pair of clustering models generated on the studied data sets. It is also possible to trace back the evolution of a given final cluster down to the initial clustering model.

4 Conclusions and Future Work

In this paper, we have proposed a sequential partitioning algorithm that groups distinct snapshots of streaming data so that a clustering model is generated on each data snapshot. It enables to deal with both incremental and dynamic aspects of modeling evolving behavior problems. In addition, the proposed approach is able to trace back evolution through the detection of clusters’ transitions. We have initially evaluated our algorithm on household electricity consumption data. The obtained results have shown that it is robust to modeling evolving data behavior by being enable to mine changes and adapt the model, respectively.

For future work, we aim to further study and evaluate the proposed clustering algorithm on evolving data phenomena in different application domains.