1 Introduction
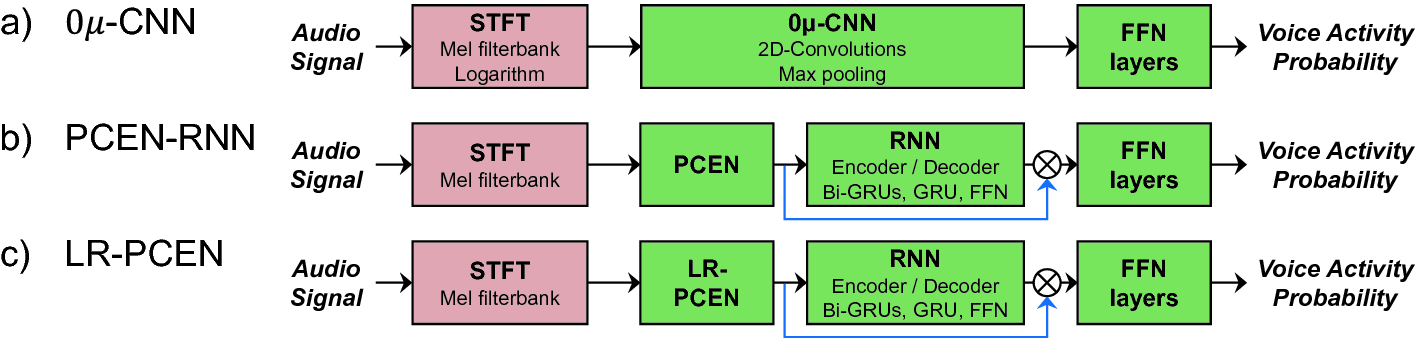
The three examined DL models. Red modules denote non-trainable, predefined functions. Green modules denote parameterized functions subject to optimization. The cross symbol  denotes the element-wise multiplication introduced in [11]. (Color figure online)
denotes the element-wise multiplication introduced in [11]. (Color figure online)
As the system used in [2], early approaches to SVD [14, 15] typically consist of two parts—the extraction of audio features and the supervised training of classifiers such as random forests. Recently, SVD based on deep learning (DL) has become popular [7–9, 17]. As for the contributions of this paper, we apply several state-of-the-art (SOTA) approaches [11, 18, 23]—proposed for SVD in popular music—to the opera scenario. We systematically assess their efficacy on a limited dataset comprising three semi-automatically annotated versions of Richard Wagner’s opera “Die Walküre” (first act). Our experiments demonstrate that the models do not sufficiently generalize across versions even when the training data contains other versions of the same musical work. Finally, we highlight specific challenges in Wagner’s operas, pointing out interesting correlations between errors and the voices’ registers as well as the activity of specific instruments.
2 Deep-Learning Methods
In this paper, we examine three SVD approaches based on supervised DL (Fig. 1).1 Lee et al. [6] give an overview and a quantitative analysis of DL-based SVD systems. Our first model (Fig. 1a) is based on a convolutional neural network (CNN) followed by a classifier module. CNNs have been widely used for SVD [16–18]. To achieve sound-level-invariant SVD, Schlüter et al. [18] introduce zero-mean convolutions—an update rule that constrains the CNN kernels to have zero mean. We use this zero-mean update rule within the specific architecture presented in [18] for our first model (denoted as  -CNN). As an alternative approach to sound-level-invariant SVD, Schlüter et al. [18] suggest per-channel energy normalization (PCEN) [23]. For our second model (Fig. 1b, denoted as PCEN-RNN), we consider this technique as front-end followed by recurrent layers and the classifier, realized by feed-forward network (FFN) layers. Recurrent neural networks (RNNs) have been used for SVD in [7], among others. As our third model, we examine a straightforward extension to PCEN involving a low-rank autoencoder (Fig. 1c, denoted as LR-PCEN). For both RNN-based models (PCEN-RNN and LR-PCEN), we include skip-filtering connections [11], which turns out to be useful for “pin-pointing” relevant parts of spectrograms [10].
-CNN). As an alternative approach to sound-level-invariant SVD, Schlüter et al. [18] suggest per-channel energy normalization (PCEN) [23]. For our second model (Fig. 1b, denoted as PCEN-RNN), we consider this technique as front-end followed by recurrent layers and the classifier, realized by feed-forward network (FFN) layers. Recurrent neural networks (RNNs) have been used for SVD in [7], among others. As our third model, we examine a straightforward extension to PCEN involving a low-rank autoencoder (Fig. 1c, denoted as LR-PCEN). For both RNN-based models (PCEN-RNN and LR-PCEN), we include skip-filtering connections [11], which turns out to be useful for “pin-pointing” relevant parts of spectrograms [10].
For pre-processing, we partition the monaural recording into non-overlapping segments of length 3 s. Inspired by previous approaches [6, 7, 18], we compute a 250-band mel-spectrogram for each segment. As input to the  -CNN model [17], we use the logarithm of the mel-spectrogram. For the PCEN-RNN model, we use the mel-spectrogram as input to the trainable PCEN front-end [23] followed by a bi-directional encoder with gated recurrent units (GRUs) and residual connections [11]. The decoder predicts a mask (of the original input size) for filtering the output of the PCEN. For the LR-PCEN, we replace the first-order recursion [23, Eq.(2)] with a low-rank (here: rank one) autoencoder that shares weights across mel-bands. The output of the autoencoder is used alongside residual connections with the input mel-spectrogram. We randomly initialize the parameters and jointly optimize these using stochastic gradient descent with binary cross-entropy loss and the Adam [5] solver setting the initial learning rate to
-CNN model [17], we use the logarithm of the mel-spectrogram. For the PCEN-RNN model, we use the mel-spectrogram as input to the trainable PCEN front-end [23] followed by a bi-directional encoder with gated recurrent units (GRUs) and residual connections [11]. The decoder predicts a mask (of the original input size) for filtering the output of the PCEN. For the LR-PCEN, we replace the first-order recursion [23, Eq.(2)] with a low-rank (here: rank one) autoencoder that shares weights across mel-bands. The output of the autoencoder is used alongside residual connections with the input mel-spectrogram. We randomly initialize the parameters and jointly optimize these using stochastic gradient descent with binary cross-entropy loss and the Adam [5] solver setting the initial learning rate to  and the exponential decay rates for the first- and second-order moments to 0.9. We optimize over the training data for 100 iterations and adapt the learning rate depending on the validation error. Moreover, we perform early stopping after 10 non-improving iterations.
and the exponential decay rates for the first- and second-order moments to 0.9. We optimize over the training data for 100 iterations and adapt the learning rate depending on the validation error. Moreover, we perform early stopping after 10 non-improving iterations.
3 Dataset
We evaluate the systems on a novel dataset comprising three versions of Wagner’s opera “Die Walküre” (first act) conducted by Barenboim 1992 (Bar), Haitink 1988 (Hai), and Karajan 1966 (Kar), each comprising 1523 measures and roughly 70 min of music. Starting with the libretto’s phrase segments, we manually annotate the phrase boundaries as given by the score (in musical measures/beats). To transfer the singing voice segments to the individual versions, we rely on manually generated measure annotations [24]. Using the measure positions as anchor points, we perform score-to-audio synchronization [3] for generating beat and tatum positions, which we use to transfer the segmentation from the musical time of the libretto to the physical time of the performances.
 recording, which we use as test version in our experiments. Almost every phrase boundaries was adjusted, thus affecting rouhgly 4% of all frames in total. Due to our annotation strategy, there might be another issue. Since we start from the libretto with its phrase-level segments, the annotations do not account for smaller musical rests within textual phrases—an issue that is also common for SVD annotations in popular music. To estimate the impact of these gaps within phrases (labeled as “singing”), we compute the overlap between the phrase-level singing regions from the libretto (
recording, which we use as test version in our experiments. Almost every phrase boundaries was adjusted, thus affecting rouhgly 4% of all frames in total. Due to our annotation strategy, there might be another issue. Since we start from the libretto with its phrase-level segments, the annotations do not account for smaller musical rests within textual phrases—an issue that is also common for SVD annotations in popular music. To estimate the impact of these gaps within phrases (labeled as “singing”), we compute the overlap between the phrase-level singing regions from the libretto ( ) and note-level annotation derived from an aligned score. The two annotations match for only 94% of all frames. This suggests that in the opera scenario, phrase-level annotations as well as automatic alignment strategies may not be precise enough for high-quality SVD evaluated on the frame level. We therefore regard an accuracy or F-measure of 94% as a kind of upper bound for our experiments.
) and note-level annotation derived from an aligned score. The two annotations match for only 94% of all frames. This suggests that in the opera scenario, phrase-level annotations as well as automatic alignment strategies may not be precise enough for high-quality SVD evaluated on the frame level. We therefore regard an accuracy or F-measure of 94% as a kind of upper bound for our experiments.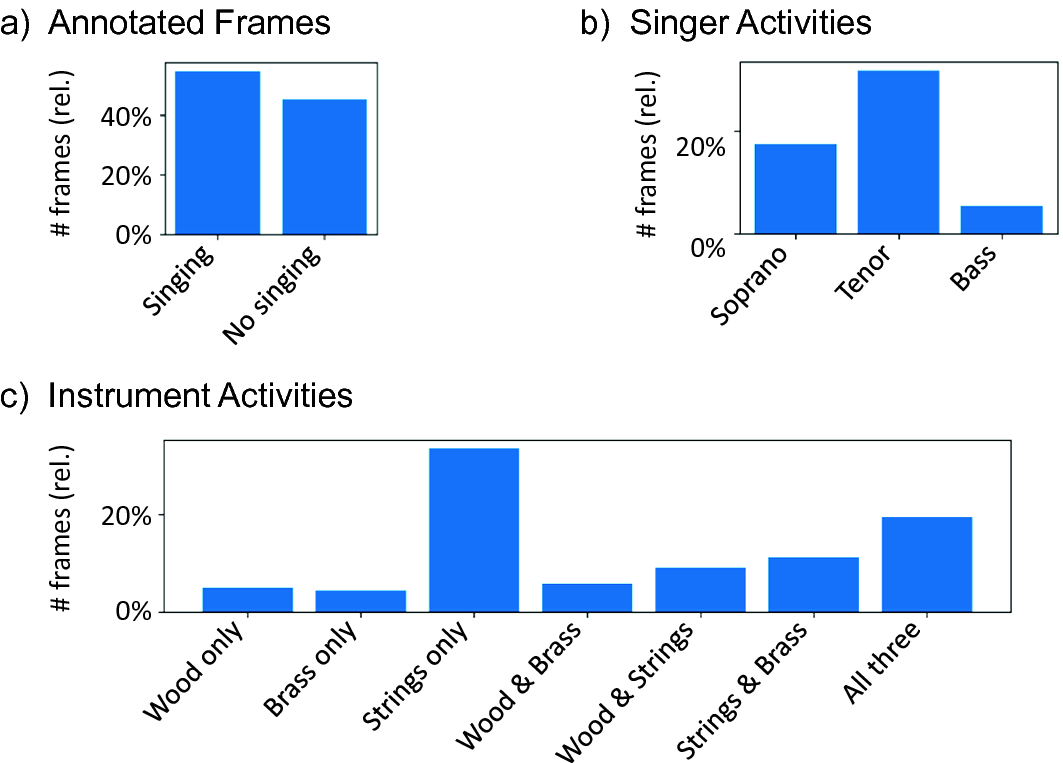
Percentage of frames ( version) with (a) annotated singing voice, (b) activity of individual singers, (c) activity of instrument sections and their combination.
version) with (a) annotated singing voice, (b) activity of individual singers, (c) activity of instrument sections and their combination.
Data splits used for the experiments.
Data split | DS-1 | DS-2 | DS-3 |
|---|---|---|---|
Training | Bar, Hai, | Bar, Hai | Bar |
Validation |
|
| Hai |
Test |
|
|
|
In our dataset, singing and non-singing frames are quite balanced (Fig. 2a). Among the three singers performing in the piece, the tenor dominates, followed by soprano and bass (Fig. 2b), while they never sing simultaneously. Regarding instrumentation, the string section alone plays most often, followed by all sections together, and other constellations (Fig. 2c). For systematically testing generalization to unseen versions, we create three data splits (Table 1). In DS-1, the test version ( ) is available during training and validation. DS-2 only sees the test version at validation. DS-3 is the most realistic and restrictive split.
) is available during training and validation. DS-2 only sees the test version at validation. DS-3 is the most realistic and restrictive split.
4 Experiments
 -CNN. In the scenario DS-3, where the
-CNN. In the scenario DS-3, where the  version is only used for testing, the results further deteriorate. Again, all models show a clear tendency towards false negatives (most prominently
version is only used for testing, the results further deteriorate. Again, all models show a clear tendency towards false negatives (most prominently  -CNN). This points to detection problems in presence of the orchestra, which become particularly relevant when generalizing to unseen versions with different timbral characteristics and acoustic conditions.
-CNN). This points to detection problems in presence of the orchestra, which become particularly relevant when generalizing to unseen versions with different timbral characteristics and acoustic conditions.SVD results for all models ( -CNN, PCEN-RNN, LR-PCEN) and data splits.
-CNN, PCEN-RNN, LR-PCEN) and data splits.
Data split Models | DS-1 | DS-2 | DS-3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PCEN-RNN | LR-PCEN |
| PCEN-RNN | LR-PCEN |
| PCEN-RNN | LR-PCEN | |
Precision |
| 0.93 | 0.94 |
| 0.91 | 0.92 |
| 0.87 | 0.90 |
Recall | 0.91 |
| 0.90 | 0.81 |
|
| 0.69 |
| 0.74 |
F-Measure |
|
| 0.92 | 0.88 | 0.89 |
| 0.80 | 0.81 |
|
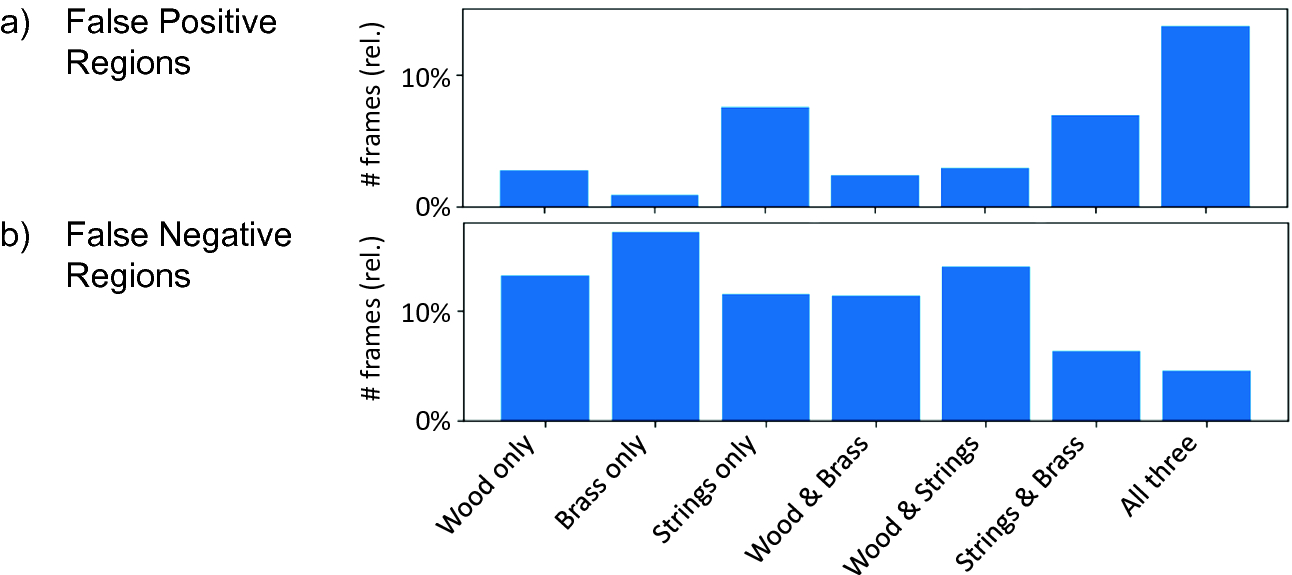
(a) False positive and (b) false negative frames as detected by the  -CNN model (
-CNN model ( version). We plot the percentage of errors for regions with certain instrument sections or constellations playing, in relation to these regions’ total duration.
version). We plot the percentage of errors for regions with certain instrument sections or constellations playing, in relation to these regions’ total duration.
We want to study such hypotheses in more detail for the realistic split DS-3. Regarding individual singers, the  -CNN model obtains higher recall for the bass (74% of frames detected) than for tenor and soprano (each 68%). Interestingly, both PCEN models behave the opposite way, obtaining low recall (<50%) for the bass and high recall (almost 80%) for the others. We might conclude that the
-CNN model obtains higher recall for the bass (74% of frames detected) than for tenor and soprano (each 68%). Interestingly, both PCEN models behave the opposite way, obtaining low recall (<50%) for the bass and high recall (almost 80%) for the others. We might conclude that the  -CNN is less affected by the imbalance of singers in the training data. Since segments typically imply a certain length, we conduct a further experiment using median filtering for removing short segments in a post-processing step (not shown in the table). As observed in [2], F-measures improve by 2–4% for all models using a median filter of roughly one second length.
-CNN is less affected by the imbalance of singers in the training data. Since segments typically imply a certain length, we conduct a further experiment using median filtering for removing short segments in a post-processing step (not shown in the table). As observed in [2], F-measures improve by 2–4% for all models using a median filter of roughly one second length.
Finally, we want to investigate correlations between errors and specific instrument activities for the LR-PCEN model’s results (Fig. 3). For most instrument combinations, we cannot observe any strong preference for producing false positives or negatives, with two interesting exceptions. When only brass instruments are playing without singing, the LR-PCEN practically never produces false positive predictions. In contrast, when brass only occurs together with singing, we observe a strong increase of false negatives. The highest frequency of false positives occurs for tutti passages (all three sections playing). When listening to false-positive regions, we often find expressive strings-only passages. In contrast, false-negative regions often correspond to soft and gentle singing. Examining this in more detail, we observed a slight loudness-dependency for all models. As reported for popular music [18], singing frames are usually louder leading to more “loud” false positives and “soft” false negatives. This indicates that, despite the models’ level invariance, confounding factors such as timbre or vibrato might affect SVD quality.
Our experiments and analyses only provide a first step towards understanding the challenges of SVD in complex opera recordings. From the results, we conclude that the systems do not sufficiently generalize across versions due to their different acoustic characteristics—even if the specific musical work is part of the training set. While all models are capable of fitting the data to a reasonable degree (given the reliability and precision of our annotations), generalization becomes problematic as soon as the test version is not seen during training or validation. Even if loudness dependencies are eliminated, our results suggest that more work has to be done to impose further invariances and constraints. A nice example is given in [21] where the generalization performance of the models is optimized. Furthermore, considering techniques such as data augmentation or unsupervised domain adaptation [4] might be useful to achieve robust SVD systems for the opera scenario.
This work was supported by the German Research Foundation (AB 675/2-1, MU 2686/11-1, MU 2686/7-2). The International Audio Laboratories Erlangen are a joint institution of the Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) and Fraunhofer Institut für Integrierte Schaltungen IIS. We thank Cäcilia Marxer and all students who helped preparing the data and annotations.



















