1 Introduction
Musical instruments recognition and sound characterization is a common subject of research in many different areas related to audio and music. Up to now several studies explored the identification of musical instruments of different classes (e.g. distinguishing a saxophone from a piano) but to the best of our knowledge, little research has been conducted to identify different types of the same instrument, for example distinguishing a Les Paul guitar from a Stratocaster model.
Johnson and Tzanetakis [1] studied the classification of guitars, mostly acoustic guitars, using hand-crafted features such as Mel-Frequency Cepstral Coefficients (MFCC), spectral moments, zero crossing rate and other features typically used in Musical Information Retrieval. They concluded that guitar models have unique sound characteristics that allows the use of classification algorithms such as k-Nearest Neighbours (kNNs) and Support Vector Machines (SVMs) to identify different guitar types. In their conclusion they state overall results with an accuracy just above 50%.
Setragno et al. [2] used feature-based analysis to investigate timbral characteristics of violins discerning two classes of violins (historical and modern) using machine learning techniques.
The goal of our study presented in this paper is to use feature-based representations and machine learning classification methodologies to classify different models of electrical guitars from two different manufacturers. A guitar model refers to a specific guitar type with certain design and construction characteristics chosen by its manufacturer.
2 Methodology
2.1 Electric Guitars Audio Recordings Dataset
To populate the dataset we recorded single notes of 17 electric guitars: 6 Fender Stratocasters, 3 Fender Telecasters, 3 Epiphone Les Pauls, 1 Epiphone Casino, 1 Epiphone Dot and 3 Epiphone SGs. All recordings were performed by the same musician, using all pickup positions and playing notes in different frets of the neck. The single notes recorded include all open strings, and notes from an A minor scale starting at the fifth fret of the sixth string played using a 3 notes per string pattern.
Number of notes recorded from each electric guitar model
Brand | Model | No. of notes |
|---|---|---|
EPIPHONE | LES PAUL STANDARD | 202 |
EPIPHONE | SG | 188 |
FENDER | SQUIER STRATOCASTER MOD. VINTAGE | 183 |
FENDER | SQUIER STRATOCASTER MOD. SM | 169 |
FENDER | AMERICAN STRATOCASTER STD HSS | 168 |
FENDER | AMERICAN STRATOCASTER STD | 162 |
FENDER | STRATOCASTER STD SPECIAL TREMOLO (MEX) | 155 |
FENDER | STRATOCASTER STD (MEX) | 152 |
FENDER | JAP. TELECASTER REI. ’62 CUSTOM MOD | 99 |
EPIPHONE | CASINO | 96 |
EPIPHONE | DOT | 95 |
EPIPHONE | LES PAUL STUDIO | 94 |
EPIPHONE | SG PRO | 92 |
FENDER | TELECASTER (MEX) | 92 |
FENDER | SQUIER TELECASTER | 92 |
In this paper we study two machine classification tasks: one classifying each note according to the manufacturer of the guitar model (two classes) and another using 4 classes in order to distinguish Fender Stratocasters, Fender other models, Epiphone Les Pauls and Epiphone other models.
The fact that there are more Fender guitars in the dataset and that the Fender Stratocaster has usually 5 pickup positions whereas the Epiphones have normally 3 pickup positions, results in the dataset to be highly imbalanced. To account for this problem we create two subsets by applying a random under-sampler from the Imbalanced-learn (version 0.4.2) [3] package for Python to under-sample the majority class to achieve an equal number of observations for each class. One subset is used for Binary Classification and another subset is used in the Multiclass Classification problem. We refer to an observation in this paper as a member of the dataset.
The total number of notes is 2040: 1273 notes from Fender guitars and 767 from Epiphone guitars. After random undersampling, the subset used for the binary classification experiment resulted in 767 notes from each guitar manufacturer. For the classification experiment with 4 classes, there are 990 notes from Fender Stratocasters, 296 notes from Epiphone Les Pauls, 471 from other models of Epiphone and 283 notes from Fender Telecasters resulting in a subset after the random under-sampling with 283 notes per class.
We split the subsets into training/testing sets with a 0.25 ratio of audio recordings in the testing set randomly preserving the percentage of observations for each class.
2.2 New Approach: Feature Analysis and Classification Algorithm
To perform the machine learning classification experiments we extracted features typically used in Music Information Retrieval (MIR) such as Mel-Frequency Cepstral Coefficients (MFCC), the Constant-Q Transform (CQT), and spectral features (centroid, bandwidth, contrast, flatness, kurtosis and skewness).
The audio files are loaded into Python 3.5 using Librosa (version 0.5.1) [4] keeping its original sample rate and bit-depth and are processed using overlapping frames with 2048 audio samples and a hop length of 1024, or 50% overlap.
A challenging point in these classification tasks is that we are dealing with audio recordings of different duration. It’s a common practice in many cases to trim or zero-pad audio files in order to have a fixed number of audio samples for all audio recordings.
In our experiments we decided to extract the features from the audio recordings using all audio samples resulting in features vectors with a different number of frames. To have features vectors with the same number of features for all observations we average the features from frames that lie inside the same energy band. We refer to an energy band as frames that lie inside two Root-Mean-Square (RMS) energy percentage boundaries (e.g. RMSE percentage between 22% and 11%). The final features vector is a flattened version of the averaged features. Because we are dealing with frame-based calculations, the borders of the energy bands can vary slightly as we are taking the first element bigger than the calculated energy border value.
218 frames. We then compute 10 RMS energy bands and discard the frames inside the first and the last bands. We average the MFCCs of frames inside the same energy bands resulting in 84 coefficients 
8 frames. The final features vector used is a normalized flattened version with 672 elements.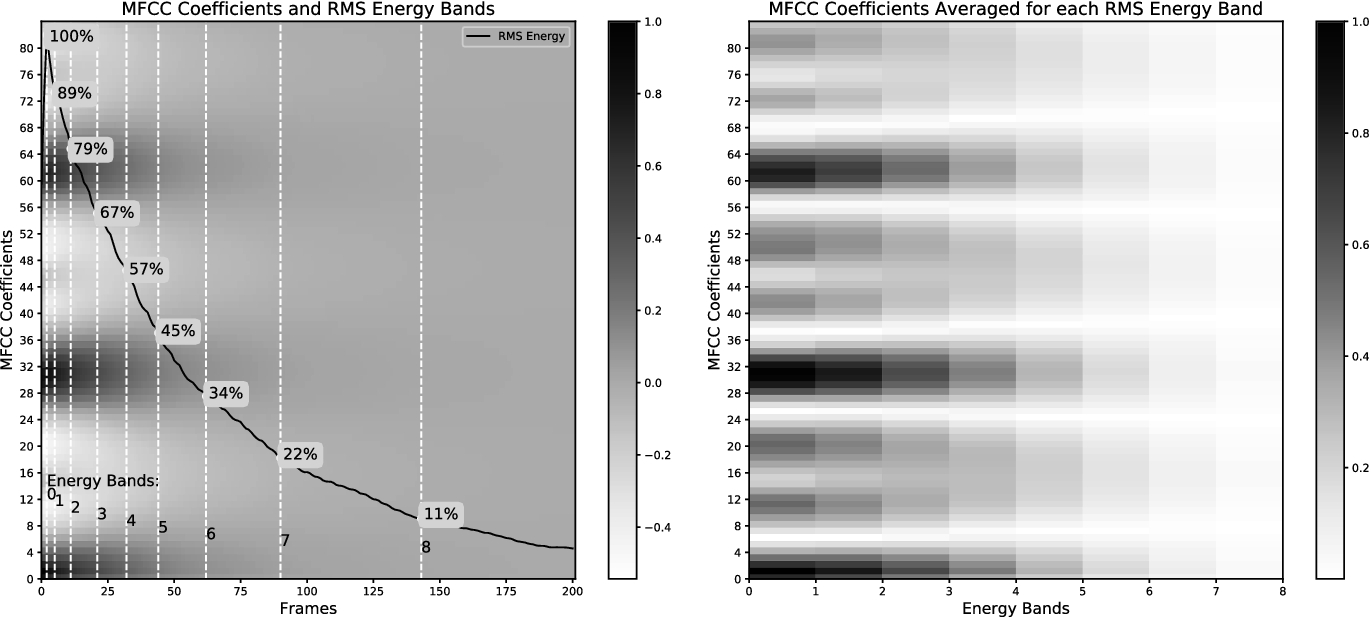
RMS energy bands averaging procedure example.
We use three different sets of features: Spectral Features, MFCCs Features and the Constant-Q Transform Features. Librosa [4] is used to extract all features with the same frame length of 2048, a hop length of 1024 audio samples and the Hann window. Features are standardized to have zero mean and unit variance.
Spectral Features. The spectral features vector consists of a vector with the spectral centroid, spectral contrast, spectral bandwidth, spectral flatness, spectral kurtosis and spectral skewness calculated for each frame and averaged using the RMS energy bands averaging procedure as explained before. The result is a vector with 48 elements (6 spectral features 
8 energy bands) per observation.
Mel-Frequency Cepstral Coefficients. The MFCC features vector is extracted using 84 coefficients resulting in a features vector with 672 elements per observation.
Constant-Q Transform. The Constant-Q transform is calculated using a total of 84 bins, 12 bins per octave, resulting in a features vector with 672 elements per observation.
Classification Algorithm. The classification algorithm used is the SVM using a Polynomial kernel with degree equals to 3, the Penalty Parameter C equals to 0.01 and the kernel coefficient Gamma of 1.0. The classification experiment is run using Scikit-Learn (version 0.20.0) [5] library for Python.
The features and classification algorithm selected are chosen observing the results from previous works in similar tasks by Johnson and Tzanetakis [1], and Setragno et al. [2] as a starting point and all the hyperparameters are tuned empirically with tryouts from many experiments. In contrast to the works mentioned above, our study is focused solely in electric guitars, we are including the Constant-Q Transform as an audio feature, and we are interested in discerning models from two different manufacturers.
3 Classification Experiments
3.1 Binary Classification
Binary classification results
Spectral | MFCC | CQT | ||||
|---|---|---|---|---|---|---|
Evaluation | Epiphone | Fender | Epiphone | Fender | Epiphone | Fender |
Recall | 76.6% | 72.4% | 75.0% | 84.4% | 95.3% | 94.3% |
Precision | 73.5% | 75.5% | 82.8% | 77.1% | 94.3% | 95.3% |
F1- Score | 75.0% | 73.9% | 78.7% | 80.6% | 94.8% | 94.8% |
Accuracy | 74.0% (286/384) | 80.0% (306/384) | 95.0% (364/384) | |||
3.2 Multiclass Classification
Multiclass classification results
Spectral Features | ||||
|---|---|---|---|---|
Evaluation | Epiphone Les Paul | Epiphone Others | Fender Stratocaster | Fender Others |
Recall | 57.7% | 52.1% | 47.1% | 62.0% |
Precision | 54.3% | 45.1% | 63.5% | 63.8% |
F1- Score | 54.3% | 48.4% | 54.1% | 63.0% |
Accuracy | 55.0% (155/283) | |||
MFCC Features | ||||
Evaluation | Epiphone Les Paul | Epiphone Others | Fender Stratocaster | Fender Others |
Recall | 50.7% | 42.3% | 32.9% | 62.0% |
Precision | 45.0% | 41.1% | 40.0% | 61.1% |
F1- Score | 47.7% | 41.7% | 39.7% | 61.1% |
Accuracy | 47.0% (133/283) | |||
CQT Features | ||||
Evaluation | Epiphone Les Paul | Epiphone Others | Fender Stratocaster | Fender Others |
Recall | 87.3% | 74.5% | 68.6% | 80.3% |
Precision | 72.9% | 79.1% | 81.4% | 79.2% |
F1- Score | 79.5% | 76.8% | 74.4% | 79.7% |
Accuracy | 78.0% (220/283) | |||
CQT + (Spectral * 2) Features | ||||
Evaluation | Epiphone Les Paul | Epiphone Others | Fender Stratocaster | Fender Others |
Recall | 91.5% | 71.8% | 81.4% | 80.3% |
Precision | 72.2% | 83.6% | 86.4% | 86.4% |
F1- Score | 80.7% | 77.3% | 83.8% | 83.2% |
Accuracy | 81.0% (230/283) | |||
4 Conclusion
In this study we conducted feature-based machine learning classification experiments to distinguish guitars from different manufacturers and models.
We recorded 17 different guitars from two manufacturers: Fender and Epiphone. We used three sets of features (spectral features, MFCCs and CQT) and one classification algorithm (SVM). The CQT features vector achieved an accuracy of 95% in a binary classification problem, correctly predicting the manufacturer of 364 guitar notes out of the total of 384. In the multiclass classification problem, the spectral and MFCC had a very poor performance, and a weighted concatenation of the CQT features with the spectral feature values multiplied by 2 obtained an accuracy of 81% with 230 correct predictions from 283 notes.
Due to the substantial difference between the datasets used, it is not possible to compare the results of our study with the previous studies mentioned. Johnson and Tzanetakis [1] studied mostly acoustic guitars and they addressed, among other things, the influence of the acoustics of the room where the acoustic guitars were recorded in their work. This issue is not present in our work with electric guitars.
It seems to us that common Music Information Retrieval features and standard machine learning classification algorithms have a good performance for binary classification of guitar notes from two quite distinctly sounding manufacturers and models. However, more complex tasks, such as distinguishing similar sounding guitars requires different techniques for features extraction and classification.
The dataset of electric guitars recordings is constantly being expanded with different models and manufacturers. This will allow more complex and reliable experiments. In future work we plan to use Deep Learning techniques and explore generative models for different applications and problems.