6

ORGANIZANDO INFORMAÇÃO PARA AS DECISÕES MAIS DIFÍCEIS

Quando a vida está em jogo

“Nada que seja perfeitamente solucionável chega à minha mesa”, observou o presidente Obama.1 “Caso contrário, alguém já teria solucionado.”

Qualquer decisão cuja solução é óbvia — que não precise de muito esforço mental — vai ser resolvida por alguém abaixo do presidente. Ninguém deseja desperdiçar o precioso tempo dele. As únicas decisões que chegam a ele são as que desnortearam todo mundo abaixo dele.

A maioria das decisões que o presidente dos Estados Unidos precisa tomar possui sérias implicações — perda de vidas em potencial, escalada de tensão entre países, mudanças na economia que podem levar ao desemprego. E os problemas costumam vir acompanhados de informação precária e pobre. Seus conselheiros não precisam dele para debater novas possibilidades — embora ele às vezes também faça isso. Os conselheiros não passam o problema para o andar de cima por serem incapazes de solucioná-lo, mas porque ele invariavelmente envolve uma escolha entre duas perdas, dois desfechos negativos, e o presidente precisa decidir qual o mais palatável. A esta altura, diz o presidente Obama, “você acaba lidando com probabilidades. Para qualquer decisão que toma, acaba com 30% ou 40% de chance de não dar certo”.

Falei de Steve Wynn, CEO da Wynn Resorts, no Capítulo 3. Eis o que ele diz sobre a tomada de decisão: “Em qualquer organização suficientemente grande, com um sistema de gestão efetivo, vai haver uma estrutura piramidal, com tomadores de decisão em cada nível. A única situação em que me envolvo é quando as soluções conhecidas têm um contra, como a perda do emprego de alguém ou a perda de grandes somas pela companhia. E geralmente a decisão já vem enquadrada para mim sob a forma de duas negativas. Cabe a mim decidir com qual dessas negativas poderemos conviver”.2

A tomada de decisão médica muitas vezes é bastante parecida — escolher entre duas negativas. Temos um desafio diante de nós: a possibilidade da deterioração da saúde se não fizermos nada ou um grande potencial de dor, desconforto e despesa se escolhermos um dos procedimentos médicos. Tentar avaliar os resultados de modo racional pode ser muito desgastante.

A maior parte de nós está mal equipada para calcular sozinha tais probabilidades. Não apenas somos mal equipados para calcular as probabilidades, mas não fomos treinados para avaliá-las racionalmente. Todos os dias precisamos enfrentar decisões que causam impacto sobre nossas vidas, nosso bem-estar e nossa saúde, e a maioria dessas decisões — ainda que não percebamos de imediato — se reduzem a probabilidades. Se o médico começa a explicar as escolhas médicas em termos de probabilidade, é provável que o paciente não compreenda a informação de maneira útil. As informações nos são dadas durante um período de extrema vulnerabilidade emocional e sobrecarga cognitiva. (Como você se sente quando recebe um diagnóstico?) Enquanto o médico discute a chance de 35% disso e a chance de 5% daquilo, nossas mentes estão distraídas, pensando nas contas de hospital e do seguro, e em como pediremos dispensa do trabalho. A voz do médico recua para o segundo plano enquanto imaginamos a dor, o desconforto, se nosso testamento está atualizado, e quem cuidará do cachorro enquanto estivermos no hospital.

Este capítulo fornece algumas singelas ferramentas para organizar informação sobre saúde, e elas se aplicam a todas as decisões mais difíceis que precisamos tomar. Mas a complexidade da informação médica provoca inevitavelmente emoções fortes, enquanto lutamos com fatores desconhecidos e até mesmo com o significado de nossas vidas. A tomada de decisão médica apresenta um profundo desafio à mente organizada, a despeito da quantidade de assistentes que você tenha, ou da sua competência nas coisas que faz.

Pensando com clareza sobre as probabilidades

A tomada de decisão é difícil porque, por sua própria natureza, envolve a incerteza. Se não houvesse incertezas, as decisões seriam fáceis! A incerteza existe porque não conhecemos o futuro, não sabemos se a decisão que tomamos levará ao desfecho mais feliz possível. A ciência cognitiva nos ensinou que ficar na dependência da intuição pode levar a decisões ruins, sobretudo nos casos em que existe informação estatística disponível. Nosso cérebro não evoluiu para lidar com o pensamento probabilístico.

Pense numa mulher de quarenta anos que deseja ter filhos. Ela lê que, comparada a uma mulher mais jovem, terá cinco vezes mais chances de ter uma criança com um defeito congênito. À primeira vista, isso parece um risco inaceitável. Pedem-lhe que aposte seu forte desejo emocional de ter filhos contra um conhecimento estatístico intelectual. Será que o conhecimento estatístico pode preencher essa lacuna e levá-la à conclusão certa, que lhe proporcionará uma vida mais feliz?

Em parte, manter uma mente e uma vida organizadas exige que tomemos as melhores decisões possíveis. As más decisões nos roubam força e energia, sem falar no tempo que talvez tenhamos que dedicar a rever a decisão se as coisas derem errado. Pessoas ocupadas, que tomam muitas decisões de alto risco, tende a dividir suas tomadas de decisão em categorias, fazendo uma triagem semelhante às listas de que falei no Capítulo 3:

1. Decisões que você pode tomar de imediato porque a solução é evidente.
2. Decisões que você pode delegar a alguém com mais tempo e perícia do que você.
3. Decisões para as quais você possui todas as informações relevantes, mas que precisam de tempo para ser digeridas ou processadas. É geralmente o caso dos juízes em processos complicados. Não é que eles não tenham a informação — e sim que desejam ponderar os vários ângulos e considerar a causa sob uma perspectiva mais ampla. É bom se atribuir um prazo final nesses casos.
4. Decisões que exigem mais informação. Nessa altura, ou você manda um assistente obter essa informação ou faz um lembrete a você mesmo para obtê-la. É bom atribuir um prazo final para as duas opções, mesmo que ele seja arbitrário, de modo que você possa riscar esse item de sua lista.

As decisões médicas às vezes recaem na categoria 1 (faça já), como quando seu dentista diz que você está com uma nova cárie e que é preciso obturá-la. As obturações são corriqueiras, as alternativas não implicam nenhum debate sério. É provável que você já tenha feito obturações antes, ou conheça pessoas que já fizeram. Há riscos, mas eles, sem dúvida, são preferíveis às sérias complicações que poderiam resultar de não obturar a cárie. A expressão sem dúvida é importante aqui; seu dentista não precisa perder tempo explicando as alternativas ou consequências de não tratar o dente. A maioria dos médicos que lida com doenças sérias, porém, não goza dessa facilidade em virtude da incerteza quanto ao melhor tratamento.3

Algumas decisões médicas recaem na categoria 2 (delegue), especialmente quando a literatura parece contraditória ou opressiva. Levantamos as mãos e perguntamos “O que o senhor faria, doutor?”, na verdade, delegando a decisão a ele.

A categoria 3 (pondere) pode parecer a opção correta assim que o problema lhe é apresentado, ou depois que as categorias 2 e 4 (obtenha mais informação) foram implementadas. Afinal de contas, no caso de decisões que afetam o modo como passaremos nossos dias neste planeta, trata-se de uma prudência intuitiva não apressar a decisão.

Grande parte da decisão médica recai na categoria 4 — é simplesmente necessário obter mais informação. Os médicos podem fornecer alguma, mas o mais provável é que você precise adquirir informação suplementar que depois vai analisar para chegar a uma decisão certa para o seu caso. A intuição entranhada pode não ter evoluído no sentido de lidar instintivamente com o pensamento probabilístico, mas podemos treinar nosso cérebro numa tarde para se tornar uma máquina lógica e eficiente de tomar decisões. Se você quiser tomar decisões médicas melhores — sobretudo num período crítico, quando a exaustão emocional pode confundir o processo de tomada de decisão —, precisa conhecer um pouco a probabilidade.

Usamos o termo probabilidade na conversa corriqueira para nos referirmos a dois conceitos diferentes, e é importante diferenciá-los. Em determinado caso, falamos de cálculos matemáticos que nos informam sobre a chance de acontecer algum desfecho entre outros possíveis — um cálculo objetivo. Em outro caso, estamos nos referindo a algo subjetivo — a uma questão de opinião.

As probabilidades do primeiro tipo descrevem eventos calculáveis ou contáveis, e — o que é importante — teoricamente passíveis de repetição. Trata-se de eventos como jogar cara ou coroa e tirar três coroas seguidas, ou tirar o rei de paus do baralho, ou ganhar na mega-sena. Calculável significa que podemos atribuir valores exatos numa fórmula que vai gerar uma resposta. Contável significa que podemos determinar as probabilidades empiricamente, realizando uma experiência ou fazendo uma pesquisa e contabilizando os resultados. Dizer que são passíveis de repetição significa que podemos refazer a experiência incontáveis vezes e esperar descrições semelhantes das probabilidades dos eventos no caso.

Para muitos problemas o cálculo é fácil. Consideramos todos os resultados possíveis, o resultado que nos interessa e armamos uma equação. A probabilidade de tirar o rei de paus (ou qualquer carta) de um baralho completo é de 1 em 52, porque é possível tirar qualquer uma das 52 cartas num baralho, e estamos interessados apenas em uma. A probabilidade de pegar qualquer rei de um baralho completo é de 4 em 52, porque o baralho tem 52 cartas e estamos interessados em quatro delas. Se há 10 milhões de bilhetes vendidos de uma loteria e você compra um, a probabilidade de você vencer é de 1 em 10 milhões. É importante que se reconheça, tanto nas loterias quanto na medicina, que podemos mudar bastante uma probabilidade, mas sem nenhuma consequência no mundo real. Você pode aumentar cem vezes sua chance de ganhar na loteria comprando cem bilhetes. Mas a chance de ganhar permanece tão incrivelmente baixa, 1 em 100 mil, que o investimento não parece razoável. Você pode ler que a probabilidade de pegar uma doença pode ser reduzida em 50% se você fizer determinado tratamento. Mas se sua chance de pegar essa doença é de 1 em 10 mil, talvez não valha a pena a despesa ou os possíveis efeitos colaterais para diminuir esse risco.

Algumas probabilidades do tipo objetivo são difíceis de serem calculadas, mas, ao menos em tese, são contabilizáveis. Por exemplo, se um ami­go lhe perguntasse qual a probabilidade de tirar um straight flush num jogo de pôquer — qualquer sequência de cinco cartas do mesmo naipe —, talvez você não soubesse a solução sem consultar um livro didático sobre probabilidade. Mas, em tese, você poderia achar a resposta contando. Poderia passar o dia inteiro distribuindo cartas, durante muitos dias, e simplesmente anotar o número de vezes que recebia um straight flush; a resposta seria muito próxima da probabilidade teórica de 0,0015% (15 chances em 1 milhão). E quanto mais perseverar com a experiência — quanto mais tentativas fizer —, mais as suas contas se aproximarão da verdadeira probabilidade, computada matematicamente. Esta é a chamada lei dos grandes números: as probabilidades extraídas da observação tendem a se aproximar cada vez mais das teóricas na medida em que os exemplos vão se estendendo. A ideia importante aqui é que a probabilidade de receber um straight flush é tanto contável quanto repetível: se seus amigos fizerem a mesma experiência, obterão resultados semelhantes, desde que a repitam muitas vezes, para coletar uma grande quantidade de dados.

Outros tipos de resultados não são sequer teoricamente calculáveis, mas ainda assim permanecem contáveis. A probabilidade de um bebê nascer menino, de um casamento terminar em divórcio, de uma casa em Elm Street pegar fogo se encaixam nessa categoria.4 Com problemas assim, recorremos à observação — nós contamos porque não existe fórmula para calcular a probabilidade. Verificamos o registro de nascimentos nos hospitais da região, vasculhamos os registros de incêndios na vizinhança durante um período de dez anos. Um fabricante de automóveis pode obter informação sobre defeitos em centenas de milhares de bombas de injeção para descobrir a probabilidade de falha depois de um determinado tempo de uso.

Enquanto as probabilidades objetivas envolvem cálculo teórico ou contagem por experiência, o segundo tipo de probabilidade — subjetiva — não é nem calculável nem contável. Nesse caso, estamos usando a palavra probabilidade para exprimir nossa certeza subjetiva sobre um evento futuro. Por exemplo, se digo que há 90% de chance de eu ir à festa de Susan na próxima sexta-feira, isso não se baseia em nenhum cálculo que fiz ou que, na verdade, alguém pudesse fazer — não há nada que possa ser medido ou calculado.5 Antes, é a expressão da fé que tenho na ocorrência deste resultado. Atribuir uma percentagem assim dá a impressão de que a estimativa é precisa, mas não é.

Então, apesar de um desses tipos de probabilidade ser objetivo e o outro, subjetivo, quase ninguém nota a diferença — usamos a palavra probabilidade na linguagem corrente, aceitando cegamente este uso, tratando os dois tipos de probabilidade como a mesma coisa.

Quando ouvimos coisas como “há 60% de chance de que o conflito entre os dois países sofra uma escalada até acabar em guerra”, ou “há 10% de chance de que uma nação pérfida detone um artefato nuclear dentro de dez anos”, não se trata de probabilidades do primeiro tipo, e sim de expressões subjetivas do segundo tipo, que exprimem a medida de confiança de quem fala na futura ocorrência de tal evento.6 Os eventos desse segundo tipo não são replicáveis como os eventos do primeiro tipo. E não são calculáveis ou contáveis como as cartas do baralho ou os incêndios em Elm Street. Não temos um conjunto de nações pérfidas idênticas, com dispositivos atômicos idênticos, que possam ser observadas de modo que nos seja possível fazer uma contagem. Nesses casos, o entendido ou observador bem informado está adivinhando ao falar numa “probabilidade”, porque não se trata de probabilidade no sentido matemático. É possível que observadores competentes discordem sobre esse tipo de probabilidade, que mexe com sua subjetividade.

Tirar o rei de paus duas vezes seguidas é improvável. Improvável a que ponto? Podemos calcular a probabilidade de dois eventos multiplicando a probabilidade de um evento pela probabilidade do outro. A probabilidade de tirar o rei de paus de um baralho completo é de 1/52, tanto para a primeira vez quanto para a segunda (se você devolver o primeiro rei depois de recebê-lo, para completar o baralho de novo). Assim, 1/52 × 1/52 = 1/2704. Do mesmo modo, a probabilidade de tirar três coroas em seguida ao tirar cara ou coroa é calculada pegando-se a probabilidade de cada evento, 1/2, e multiplicando-a três vezes: 1/2 × 1/2 × 1/2 = 1/8. Você também pode fazer uma pequena experiência e jogar uma moeda três vezes seguidas muitas vezes. No final, obterá três coroas seguidas mais ou menos em um oitavo das tentativas.

Para que essa regra de multiplicação funcione, os eventos precisam ser independentes. Em outras palavras, presumimos que a carta que tirei da primeira vez não tem nada a ver com a carta que tirei da segunda vez. Se o baralho for corretamente embaralhado, isso deve ser verdade. É claro que há casos em que os eventos não são independentes. Se eu perceber que você botou o rei de paus na parte de baixo do baralho depois da minha primeira retirada e escolho a parte de baixo do baralho ao retirar minha segunda carta, os eventos não são independentes. Se um meteorologista prevê chuva para hoje e amanhã, e você quer saber a probabilidade de haver chuva em dois dias seguidos, esses eventos não são independentes, porque as frentes climáticas levam algum tempo para passar por uma região. Se os eventos não forem independentes, a matemática fica um pouco mais complicada — embora não terrivelmente.

É preciso que se considere a independência com cuidado. Ser atingido por um raio é bastante incomum — segundo o Serviço Nacional de Meteorologia dos Estados Unidos, a chance é de 1 em 10 mil.7 Então, a chance de ser atingido duas vezes é de 1/10.000 × 1/10.000 (1 chance em 100 milhões)? Isso só se sustenta se os eventos forem independentes, e eles provavelmente não são. Se você vive numa região de muitas tempestades elétricas e normalmente fica ao ar livre durante a sua ocorrência, é mais provável que seja atingido por um raio do que alguém que vive num local diferente e toma mais precauções. Um homem foi atingido por raios duas vezes em dois minutos, e um guarda florestal da Virgínia, sete vezes durante a vida.8

Seria tolice dizer: “Já fui atingido por um raio uma vez, então posso andar impunemente no meio de tempestades”. No entanto, esse tipo de pseudológica é exibido por pessoas sem noção de probabilidade. Alguns anos atrás, ouvi a conversa de um jovem casal numa agência de viagens tentando decidir a companhia aérea na qual viajariam. Foi mais ou menos assim (segundo minha memória, sem dúvida imperfeita):

Alice: Não me sinto bem viajando pela Blank Airways — eles sofreram aquele desastre ano passado.9

Bob: Mas a chance de um desastre aéreo é de 1 em 1 milhão. A Blank Air­ways acabou de sofrer um desastre. Então não vai acontecer com ela de novo.

Sem dispor de outras informações sobre as circunstâncias do desastre da Blank Airways, Alice manifesta um temor perfeitamente razoável. Os desastres de avião não costumam ser acontecimentos aleatórios; indicam potencialmente algum problema subjacente no modo de operação da companhia — pilotos mal treinados, mecânica descuidada, frota envelhecida. Dois desastres da Blank Airways em sequência não podem ser considerados dois eventos independentes. Bob está usando o “raciocínio intuitivo”, não o raciocínio lógico; é como dizer que se você já foi atingido por um raio, não poderá ser atingido de novo. Seguindo essa pseudológica ao extremo, podemos imaginar Bob argumentando: “A chance de haver uma bomba neste avião é de 1 em 1 milhão. Então, levarei uma bomba comigo, porque a chance de haver duas bombas no avião é astronomicamente improvável”.

Mesmo que os desastres de avião fossem independentes, achar que não vai acontecer agora “porque acabou de acontecer” é cair na falácia do jogador, e imaginar que um voo seguro está agora “na ordem do dia”. Os deuses da sorte não estão contando os voos para assegurar que haja 1 milhão deles antes do próximo desastre, e tampouco vão assegurar a distribuição igualitária dos próximos desastres entre as companhias aéreas que restarem. Assim sendo, a probabilidade de qualquer companhia área sofrer dois desastres em sequência não pode ser considerada algo independente.

Uma probabilidade obtida de forma objetiva não é uma garantia. Apesar de esperarmos que dê coroa na metade das vezes que jogamos uma moeda, a probabilidade não é um processo autocorretivo. A moeda não tem memória, conhecimento, força de vontade, desejo. Não existe nenhum superintendente que assegure que tudo irá funcionar como você espera. Se você tira “coroa” dez vezes em sequência, a probabilidade de a moeda dar cara na próxima jogada ainda é de 50%. Cara não é mais provável, nem “esperada”. A ideia de que os processos da sorte se corrigem faz parte da falácia do jogador, e enriqueceu muitos donos de cassinos, inclusive Steve Wynn. Milhões de pessoas continuam a enfiar moedas nos caça-níqueis na ilusão de que seu prêmio está a ponto de chegar. É verdade que as probabilidades tendem a se igualar, mas somente a longo prazo. E esse longo prazo pode ser maior e exigir mais dinheiro do que qualquer um possui.

O estranho nisso tudo é que nossa intuição diz que tirar onze caras consecutivas é muito improvável. Isso está certo — mas apenas em parte.

A falha no raciocínio vem de confundir a raridade de dez caras consecutivas com a raridade de onze caras consecutivas — na verdade, não há tanta diferença assim. Toda sequência de dez caras sucessivas só pode ser seguida de outra cara ou de uma coroa, as duas igualmente prováveis.10

Os seres humanos têm pouca noção do que constitui uma sequência aleatória. Quando nos pedem que escrevamos uma sequência aleatória, tendemos a escrever muito mais alternâncias (cara-coroa-cara-coroa) e muito menos resultados consecutivos (coroa-coroa-coroa) do que surgem nas sequências aleatórias de fato. Em uma experiência, pediu-se que as pessoas reproduzissem o que achavam que seria uma sequência aleatória de cem jogadas de cara ou coroas. Quase ninguém registrou sequências consecutivas de sete caras ou de sete coroas, mesmo havendo mais de 50% de chance de elas ocorrerem em cem jogadas.11 Nossa intuição nos leva a equilibrar a proporção cara/coroa até em sequências menores, apesar de às vezes serem necessárias sequências muito longas — de milhões de jogadas — para que se revele a proporção estável de 50/50.

Combata essa intuição! Se você jogar uma moeda três vezes consecutivamente, é verdade que só haverá uma chance de 1/8 de tirar três coroas consecutivas. Mas isso é prejudicado pelo fato de você estar observando uma sequência breve. Na média, bastam catorze jogadas para que se tire três coroas consecutivas,12 e, em cem jogadas, há uma chance maior do que 99,9% de isso acontecer pelo menos uma vez.13

O motivo de sermos enganados por esse raciocínio ilógico — segundo o qual as probabilidades mudam durante uma sequência — é que, em alguns casos, elas realmente mudam. Verdade! Se você está jogando cartas e esperando que surja um ás, a probabilidade de esta carta sair aumenta quanto maior for a sua espera. Depois que já se jogaram 48 cartas, a probabilidade de a carta seguinte ser um às é de 100% (só restam ases).14 Se você for um caçador-coletor em busca daquele grupo de árvores frutíferas que viu no verão anterior, cada setor do terreno que você esquadrinha sem achar nada aumentará sua chance de encontrá-la no próximo setor. Se você não parar para pensar com cuidado, é fácil confundir esses dois modelos probabilísticos.

Muito do que nos interessa já aconteceu antes, de modo que podemos contar ou observar com que frequência tendem a acontecer. A proporção básica de algo é a proporção de sua ocorrência no passado. A maioria de nós tem uma noção intuitiva disso. Quando você leva o carro ao mecânico porque o motor está com um barulho esquisito, mesmo antes de olhar, o mecânico talvez diga algo como “Provavelmente é a correia — em 90% dos carros é isso. Pode ser também defeito na injeção, mas a injeção raramente dá defeito”. O mecânico está usando estimativas, com conhecimento de causa, da proporção básica de algo ocorrer no mundo.

Se você foi convidado para uma festa na casa de Susan com várias pessoas que você não conhece, qual a chance de você acabar conversando com um médico em vez de um ministro de Estado? Existem mais médicos do que ministros. A proporção básica de médicos é mais alta, então, se você não sabe nada sobre a festa, sua previsão mais acertada parece ser a de que encontrará mais médicos do que ministros. Do mesmo modo, se de repente você tem uma dor de cabeça e é um sujeito preocupado, talvez tenha medo de estar com um tumor no cérebro. Dores de cabeça inexplicáveis são muito comuns; tumores no cérebro, não. O clichê no diagnóstico médico é “se tem cara de porco, pé de porco, rabo de porco, não pense em cavalo, pense em porco”. Em outras palavras, não ignore o padrão básico do que é provável, dados os sintomas.15

As experiências da psicologia cognitiva demonstraram amplamente que costumamos ignorar padrões básicos ao fazer juízos e tomar decisões. Em vez disso, favorecemos informação que pensamos ser um diagnóstico, para usar um termo médico. Na festa de Susan, se a pessoa com que você está conversando usa um broche com a bandeira americana na lapela, sabe muito sobre política e está sendo vigiada por um agente do serviço secreto, você pode concluir que se trata de um ministro, já que possui seus atributos. Mas você está ignorando a proporcionalidade básica. Existem 850 mil médicos nos Estados Unidos16 e apenas quinze ministros.17 Dos 850 mil médicos, deve haver alguns que usam broche com a bandeira americana, entendem de política e até protegidos por agentes secretos, por um motivo qualquer. Por exemplo, dezesseis congressistas do 111º Congresso eram médicos — quantidade maior que a de ministros.18 E depois há todos os médicos que trabalham para as Forças Armadas, o FBI e a CIA, e médicos cujos cônjuges, pais ou filhos são funcionários públicos com muita exposição na mídia — alguns dos quais teriam direito à proteção do serviço secreto. Alguns desses 850 mil médicos podem estar sendo investigados por motivos de segurança ou qualquer outra questão, o que justificaria o agente secreto. Essa falha de raciocínio é tão convincente que tem um nome — heurística da representatividade. Quer dizer que pessoas ou situações que parecem ser representativas de algo acabam dominando a capacidade de raciocínio do cérebro, nos fazendo ignorar a informação estatística ou de proporcionalidade básica.

Numa experiência típica na literatura científica, pedem que você leia um cenário. Diz-se que, em determinada universidade, 10% dos estudantes são engenheiros e 90% não. Você vai a uma festa e vê alguém usando um protetor de bolso de plástico (o que não é dito na descrição é que muitos consideram isso um estereótipo do engenheiro). Em seguida, pedem que você avalie a probabilidade de essa pessoa ser engenheiro. Muitos dizem ter certeza. O protetor de bolso parece ser um diagnóstico tão bom, uma prova tão conclusiva, que é difícil imaginar que a pessoa possa ser qualquer outra coisa. Mas os engenheiros são bastante raros nessa universidade, de modo que precisamos levar isso em conta. A probabilidade de essa pessoa ser engenheiro talvez não seja tão baixa quanto a proporcionalidade básica, 10%, mas também não tão alta quanto 100% — outras pessoas também podem usar protetores de bolso.

É aqui que a coisa fica interessante. Os pesquisadores então armaram o mesmo cenário — uma festa na universidade em que 10% dos estudantes são engenheiros e 90% não são — e em seguida explicaram: “Você encontra um sujeito que pode estar usando um protetor de bolso de plástico, mas não dá para ver porque ele está usando paletó”. Ao serem solicitadas a avaliar a probabilidade de que esse sujeito seja engenheiro, as pessoas geralmente respondem: “Meio a meio”. Quando lhes perguntam por quê, elas dizem: “Bem, ele poderia estar usando um protetor de bolso ou não — não dá para saber”. Aqui, vê-se novamente que não foi levada em conta a proporcionalidade básica. Se você não sabe nada sobre a pessoa, então há uma chance de 10% de que ela seja engenheiro, e não de 50%. Só porque existem apenas duas opções não quer dizer que sejam igualmente prováveis.

Para dar um exemplo intuitivamente mais claro, imagine que você entre no seu mercado local e esbarre em alguém sem querer. Qual a probabilidade de essa pessoa ser a rainha Elizabeth? A maioria das pessoas não acha que seja de 50%. Qual a probabilidade de a rainha estar em qualquer mercado, que dirá naquele onde faço minhas compras? Isso é muito improvável. Então isso mostra que somos capazes de usar informação de proporcionalidade básica quando os acontecimentos são extremamente improváveis. É só quando são ligeiramente improváveis que nosso cérebro congela. Organizar nossas decisões exige que combinemos informação de proporcionalidade básica com outras informações relevantes de diagnóstico. Este tipo de raciocínio foi descoberto no século XVIII pelo matemático e ministro presbiteriano Thomas Bayes, e leva seu nome: regra de Bayes.

A regra de Bayes nos permite refinar as estimativas. Por exemplo, lemos que metade dos casamentos termina em divórcio. Mas podemos refinar essa estimativa se tivermos informação complementar, como idade, religião ou localidade das pessoas envolvidas, porque a soma de 50% só se sustenta para a soma agregada de todas as pessoas. Algumas subpopulações têm taxas de divórcio mais altas do que outras.

Lembram-se da festa na universidade que tinha 10% de engenheiros e 90% de não engenheiros? Alguma informação complementar ajudaria a avaliar a probabilidade de que alguém com um protetor de bolso fosse engenheiro. Talvez você saiba que a anfitriã da festa rompeu feio com um engenheiro e não os convida mais para suas festas. Talvez você fique sabendo que 50% dos estudantes de medicina dessa universidade usam protetores de bolso. Informação desse tipo nos permite atualizar nossas avaliações originais básicas. Quantificar essa probabilidade atualizada é uma aplicação das inferências de Bayes.

Não estamos mais fazendo a pergunta simples, unilateral, “Qual a probabilidade de que a pessoa com o protetor de bolso de plástico seja engenheiro?”. Em vez disso, estamos fazendo a pergunta composta, “Qual a probabilidade de que a pessoa com o protetor de bolso seja engenheiro, considerando que 50% dos estudantes de medicina da universidade usam protetores de bolso?”. A raridade dos engenheiros está sendo contraposta à maior distribuição de protetores de bolso.

Também podemos fazer indagações médicas como “Qual a probabilidade de que esta dor de garganta seja um sinal de gripe, já que há três dias visitei uma pessoa gripada?”, ou “Qual a probabilidade de que esta dor de garganta seja sinal de febre do feno, já que andei fazendo jardinagem no auge da estação do pólen?”. Fazemos esse tipo de atualização informalmente na cabeça, mas existem ferramentas que podem nos ajudar a quantificar o efeito da nova informação. O problema de fazer isso informalmente é que nossos cérebros não são configurados para gerar intuitivamente respostas precisas a essas perguntas. Nossos cérebros evoluíram para solucionar uma série de problemas, mas os problemas bayesianos ainda não estão incluídos.

Ah, não! Meu exame acabou de dar positivo!

Qual a seriedade de uma notícia assim? Questões complexas como essa são facilmente resolvidas por meio de um truque que aprendi na faculdade — tabelas quádruplas (também conhecidas como tabelas de contingência).19 Elas não são facilmente resolvidas por meio da intuição ou dos palpites. Digamos que numa manhã você acorde com a visão embaçada. Suponhamos, além disso, que exista uma doença rara chamada “visão embaçada”. Em todos os Estados Unidos só existem 38 mil pessoas com esse problema, o que lhe dá uma incidência, ou proporcionalidade básica, de 1 em 10 mil (38 mil em 380 milhões). Você acabou de ler a respeito disso e agora teme estar com a doença. Por que outro motivo, você pensa, eu estaria com a visão embaçada?

Você faz exames de sangue para visão embaçada e eles dão positivo. Você e seus médicos estão tentando decidir o que fazer em seguida. O problema é que a cura da visão embaçada, um remédio chamado clorohidroxelene,20 possui a probabilidade de 20% de apresentar sérios efeitos colaterais, inclusive uma coceira terrível e irreversível, exatamente na parte das costas que não conseguimos alcançar. (Há um remédio para a coceira, mas ele tem a probabilidade de 80% de mandar a sua pressão sanguínea lá para cima.) A probabilidade de 20% lhe parece aceitável, e talvez você esteja propenso a tomar o remédio para se livrar da visão embaçada. (Esses 20% são uma probabilidade objetiva do primeiro tipo — não uma estimativa subjetiva, mas um algarismo obtido após o acompanhamento de dezenas de milhares de usuários da droga.) É natural que você queira com­preender exatamente quais as probabilidades de você ter a doença antes de tomar o remédio e correr o risco de enlouquecer de coceira.

A tabela quádrupla ajuda a dispor toda a informação de modo a se ter uma visualização fácil, e não exige nada mais complicado do que um nível simples de divisão. Se os algarismos e frações o fazem ter vontade de sair correndo da sala aos berros, não se preocupe — o apêndice traz os detalhes, e este capítulo só apresenta uma visão por alto (talvez embaçada, já que, afinal de contas, você está sofrendo de visão embaçada por enquanto).

Vamos ver a informação que temos:

• A incidência de visão embaçada é de 1 em 10 mil, ou 0,0001.
• O uso de clorohidroxelene provoca efeitos colaterais em 20% dos casos, ou 0,2.

Você talvez presuma que se o exame deu positivo, isso quer dizer que você tem a doença, mas os exames não funcionam assim — a maioria é imperfeita. E agora que você conhece algo sobre o pensamento bayesiano, talvez queira fazer uma pergunta mais refinada: “Qual a probabilidade real de eu ter a doença, considerando que o exame deu positivo?”. Lembre-se de que a incidência nos diz que a probabilidade de alguém escolhido a esmo ter a doença é de 0,0001. Mas você não é alguém escolhido a esmo. Sua visão estava embaçada, e seu médico o mandou fazer o exame.

Precisamos de mais informação para continuar. Precisamos saber qual a margem de erro que o exame apresenta, e que ele pode errar de duas maneiras. Pode indicar que você tem a doença quando não tem — um falso positivo — ou pode indicar que você não tem a doença quando tem — um falso negativo. Suponhamos que em ambos os casos seja de 2%. Na vida real, podem diferir um do outro, mas suponhamos que seja de 2% para cada caso.

Começamos por desenhar quatro células e designá-las da seguinte maneira:

Os cabeçalhos das colunas representam o fato de que o resultado do exame pode ser tanto positivo quanto negativo. Por enquanto, deixamos de lado a dúvida se esses resultados são precisos ou não — é para tirar essa conclusão que usaremos a tabela. Os cabeçalhos horizontais indicam a presença ou a ausência da doença em determinado paciente. Cada célula representa a conjunção dos cabeçalhos horizontais e verticais. Numa leitura horizontal vemos que, das pessoas que têm a doença (linha “Sim”), algumas têm resultado positivo no exame (célula superior esquerda), e outras, resultado negativo (célula superior direita). O mesmo acontece com a linha “Não”; algumas pessoas terão resultado positivo no exame, outras não. Você espera que, mesmo tendo um resultado positivo (coluna da esquerda), não tenha a doença (célula inferior esquerda).

Depois de preencher a informação que obtivemos (passo por ela com mais calma no Apêndice), podemos responder à pergunta “Qual a probabilidade de eu ter a doença, considerando que meu exame deu positivo?”.

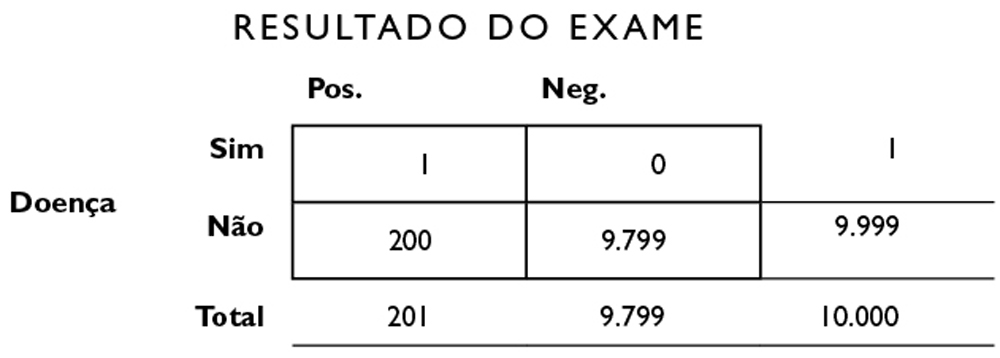
Examine a coluna que mostra as pessoas que tiveram resultado positivo no exame:

Pode-se ver que, de 10 mil pessoas, 201 (o total abaixo da coluna da esquerda) tiveram resultado positivo no exame, como você. Mas, dessas 201 pessoas, só uma tem a doença — só há uma probabilidade em 201 de que você de fato tenha a doença. Podemos pegar 1/201 × 100 para transformá-la numa percentagem e obtemos 0,49% — que não é uma alta possibilidade, como quer que a encaremos... Sua probabilidade era de 1 em 10 mil antes de fazer o exame. Agora é de 1 em 201. Ainda há a probabilidade de aproximadamente 99,51% de você não ter a doença. Se isso o faz lembrar do bilhete de loteria de que falamos antes, deveria mesmo. Sua probabilidade mudou dramaticamente, mas isso não afetou, de modo apreciável, o resultado no mundo real. A lição que se deve levar para casa é que o resultado do exame não lhe diz tudo que você devia saber — é preciso utilizar a informação da incidência e da margem de erro para ter um quadro completo. É isso que a tabela quádrupla lhe permite fazer. Não importa se a doença provoca sintomas brandos, como visão embaçada, ou sintomas muito sérios, como uma paralisia; a tabela ainda lhe permite organizar a informação em um formato facilmente digerível. Idealmente, seria bom trabalhar em contato íntimo com seu médico para considerar condições de comorbidez, sintomas que ocorrem juntos, histórico familiar e assim por diante, para tornar mais precisa a sua estimativa.

Vamos examinar a outra peça de informação, a droga milagrosa que pode curar a visão embaçada, o clorohidroxelene, que tem 1 probabilidade em 5 de provocar efeitos colaterais (20% de efeitos colaterais não é atípico para um remédio de verdade). Se você tomar o remédio, precisa comparar a probabilidade de 1 em 5 de ter uma coceira terrível nas costas com a probabilidade de 1 em 201 de que ele lhe trará a cura. Vamos colocar isso de outro modo: se 201 pessoas tomarem a droga, somente uma será curada (porque 200 não tinham de fato a doença — puxa!). Agora, dessas mesmas 201 pes­soas que tomam a droga, 1 em 5 sentirá o efeito colateral. Assim, para 1 pessoa curada, 40 pessoas acabam com aquela coceira nas costas onde não conseguem coçar. Portanto, se tomar a droga, você tem 40 vezes mais chance de sentir o efeito colateral do que de ficar curado. Infelizmente, esses resultados são típicos do moderno tratamento de saúde nos Estados Unidos.21 É de admirar que os custos estejam subindo como foguete, e fora de controle?

Um dos meus exemplos prediletos da utilidade das tabelas quádruplas eu ouvi de meu professor, Amos Tversky. Chama-se o problema dos dois venenos. Quando Amos passou uma versão desse problema para médicos de hospitais importantes e de faculdades de medicina, e também para formandos de estatística e faculdades de administração, foram tantos os que erraram a resposta, que os pacientes hipotéticos teriam morrido! Seu enfoque é que o raciocínio estatístico não nos vem de maneira natural; precisamos combater nossos tiques e aprender a elaborar os números metodicamente.

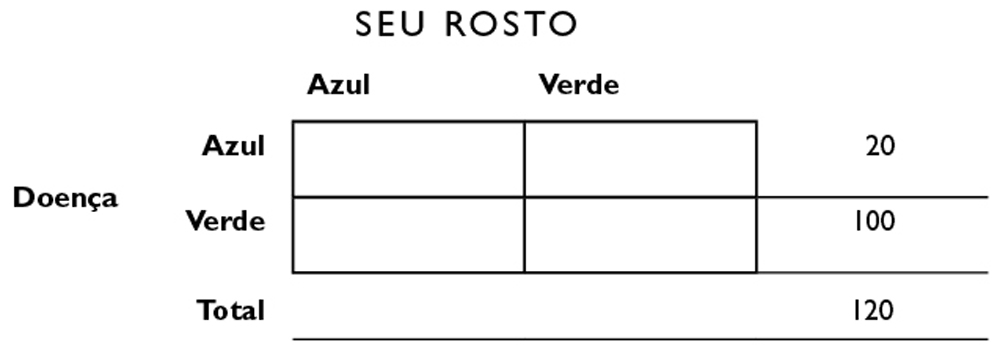
Imagine, diz Amos, que você vai a um restaurante e depois acorda se sentindo péssimo. Você olha no espelho e vê que seu rosto ficou azul. O médico do pronto-socorro lhe diz que existem dois tipos de intoxicação alimentar, uma que deixa seu rosto azul e outra que deixa seu rosto verde (nós presumimos quanto a este problema que não existam outras possibilidades de deixar seu rosto azul ou verde). Felizmente, você pode tomar um remédio para se curar. Não faz efeito se você estiver saudável, mas, se você tiver uma dessas duas doenças e tomar o comprimido errado, morre. Imagine que em 75% dos casos a cor do seu rosto é consistente com a doença, e que a doença verde é cinco vezes mais comum que a doença azul. Qual a cor do comprimido que você toma?

O palpite da maior parte das pessoas (e compartilhado pelos médicos que Amos consultou) é que deviam tomar o comprimido azul, porque (a) o rosto delas estava azul e (b) a cor do rosto delas é consistente na maior parte do tempo, 75%. Mas isso ignora as taxas básicas de incidência da doença.

Preenchemos nossa tabela quádrupla. Não nos dizem o tamanho da população com que estamos lidando, assim, para facilitar a construção da tabela, vamos supor uma população de 120 (é esse o número que vai no canto inferior direito fora da tabela).22 O problema nos fornece bastante informação para preencher o resto da tabela.

Se a doença verde é cinco vezes mais comum que a doença azul, isso significa que, de 120 pessoas que têm a doença, 100 devem ter a doença verde, e 20, a doença azul.23

Como a cor do seu rosto é consistente com a doença em 75% dos casos, 75% das pessoas com a doença azul estão com o rosto azul; 75% de 20 = 15. O resto da tabela é preenchido do mesmo modo.

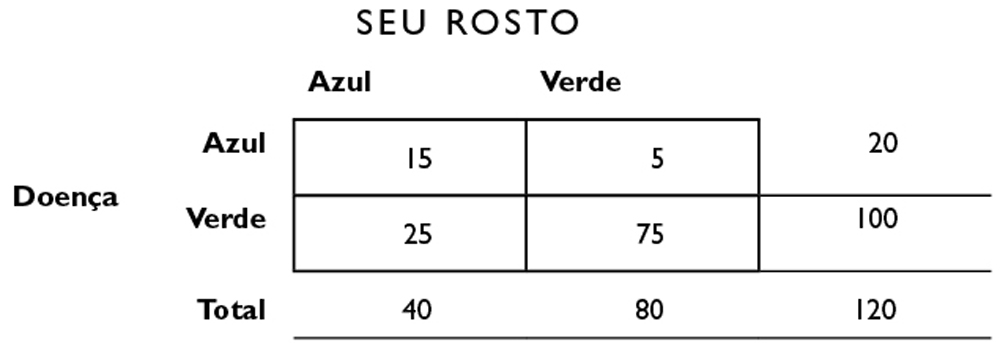
Agora, antes que você tome o comprimido azul — que tanto pode curá-lo quanto matá-lo —, a pergunta bayesiana que você precisa fazer a si mesmo é: “Qual a probabilidade de eu ter a doença azul, considerando que estou com o rosto azul?”. A resposta é que, das 40 pessoas que estão com o rosto azul, 15 têm a doença: 15/40 = 38%. A probabilidade de que você tenha a doença verde, mesmo que você esteja com o rosto azul, é de 25/40, ou 62%. É muito melhor tomar o comprimido verde a despeito da cor do seu rosto. Isto porque a doença do rosto verde é muito mais comum do que a doença do rosto azul. Novamente, estamos contrapondo taxas básicas de incidência aos sintomas, e aprendemos que as taxas de incidência não devem ser ignoradas. É difícil fazer isso nas nossas cabeças — a tabela quádrupla nos oferece uma maneira de organizar a informação visualmente, de modo que seja fácil compreendê-la. Cálculos assim são o motivo de os médicos muitas vezes começarem a prescrever antibióticos aos pacientes antes de receber os resultados de exames e descobrir exatamente o que está errado — determinados antibióticos funcionam contra tantas doenças comuns, que isso basta para justificá-los.

No exemplo da visão embaçada do início, 201 pessoas têm um exame com resultado positivo para uma doença que só uma pessoa tem. Em muitos cenários de tratamento de saúde de hoje, todas as 201 pessoas receberiam a medicação. Isso ilustra outro conceito importante da prática médica: o número de pessoas a tratar, ou seja, a quantidade de pessoas que precisam se submeter a um tratamento, como um remédio ou uma cirurgia, antes que alguém possa ser curado. Um número de pessoas a tratar da ordem de 201 não é incomum na medicina de hoje. Existem algumas cirurgias de rotina em que o número de pessoas a tratar é 48, e, quanto a alguns remédios, esse número pode exceder 300.

Rostos azuis e testes para doenças imaginárias à parte, o que dizer das decisões que nos confrontam diretamente com nossa mortalidade? Seu médico lhe diz que esses remédios lhe darão 40% de chance de viver cinco anos a mais. Como você avalia isso?

Existe uma maneira de pensar sobre essa decisão com a mesma clara racionalidade que aplicamos ao problema dos dois venenos, usando o conceito de “valor esperado”. O valor esperado de um evento é sua probabilidade multiplicada pelo valor do resultado. Empresários usam este método rotineiramente para avaliar decisões financeiras. Imagine que alguém venha até você numa festa e se ofereça para jogar um jogo com você. Ela joga uma moeda normal e você ganha 1 dólar toda vez que der cara. Quanto você pagaria para participar desse jogo? (Imagine por um momento que você não gosta tanto do jogo, embora não se incomode especialmente com ele — seu interesse é ganhar dinheiro.) O valor esperado do jogo é 50 centavos, isto é, a probabilidade de a moeda dar cara (0,5) vezes o lucro (1 dólar). Repare que o valor esperado muitas vezes não é uma quantia que você possa ganhar num lance qualquer. Aqui, você ganha 1 dólar ou não ganha nada. Mas, no decorrer de muitas centenas de repetições do jogo, você deverá ter ganhado cerca de 50 centavos por jogo. Se você pagar menos de 50 centavos por jogo, a longo prazo acabará lucrando.

Valores esperados também podem ser aplicados a perdas. Digamos que você esteja tentando decidir se paga para estacionar no Centro ou corre o risco de ser multado estacionando numa área de carga e descarga. Imagine que o estacionamento cobre 20 dólares, e que a multa seja de 50 dólares, mas você sabe por experiência que só há 25% de probabilidade de receber uma multa. Então o valor esperado de ir ao estacionamento é de –20 dólares: você tem a probabilidade de 100% de ser obrigado a pagar 20 dólares ao atendente (usei sinal de subtração para indicar que é uma perda).

A decisão é algo assim:

1. Pagar para estacionar: 100% de chance de perder 20 dólares
2. Não pagar para estacionar: chance de 25% de perder 50 dólares

O valor esperado da multa é 25% × –50 dólares, isto é, –12,50 dólares. Ora, mas você detesta multa por estacionamento em local proibido e deseja evitá-las. Talvez esteja se sentindo azarado esta noite e queira evitar riscos. Por isso, hoje, talvez pague 20 dólares para evitar a possibilidade de acabar com uma multa de 50 dólares. Mas a maneira racional de avaliar a situação é considerá-la a longo prazo. No decorrer de nossas vidas, nos defrontamos com centenas de decisões como esta. O que realmente importa é o que vamos apurar em média. O valor esperado dessa decisão em particular é que você lucrará a longo prazo pagando multas: uma perda média de 12,50 dólares contra uma perda de 20 dólares.24 Depois de estacionar um dia por semana durante um ano nessa rua em particular, você pagará 650 dólares de multas contra 1.040 dólares de estacionamento — uma grande diferença.25 É claro que em determinados dias você poderá usar uma atualização bayesiana. Se você vir um leitor de parquímetros subindo a rua em direção à sua vaga na zona de carga e descarga, é um bom dia para usar o estacionamento.

O valor esperado também pode ser aplicado a desfechos não monetários. Se dois procedimentos médicos têm eficácia e benefícios iguais a longo prazo, você pode escolher entre eles com base no tempo que exigirão de sua rotina diária.

Procedimento 1: Chance de 50% de exigir 6 semanas de recuperação e 50% de chance de exigir apenas 2 semanas

Procedimento 2: Chance de 10% de exigir 12 semanas e 90% de chance de exigir apenas 0,5 semana

Volto a usar o sinal de subtração para indicar perda de tempo. O valor esperado (em tempo) do procedimento 1 é, portanto:

(0,5 × –6 semanas) + (0,5 × –2 semanas) = –3 + –1 = –4 semanas.

O valor esperado do procedimento 2 é:

(0,1 × –12) + (0,9 × –0,5) = -1,2 + –0,45 = –1,65 semana.

Ignorando todos os outros fatores, você sai lucrando com o procedimento 2, que o afasta do trabalho aproximadamente por apenas uma semana e meia (em média), em comparação ao procedimento 1, que o afastará por 4 semanas (em média).

É claro que você talvez não consiga ignorar todos os demais fatores; minimizar o tempo de recuperação pode não ser sua única preocupação. Se você acabou de comprar passagens não reembolsáveis para um safári na África que sai em onze semanas, não pode correr o risco de uma recuperação de doze semanas. O procedimento 1 é melhor, porque, no pior dos casos, você fica preso na cama durante 6 semanas. Assim, o valor esperado é bom para avaliar médias, mas muitas vezes é necessário pesar os piores e os melhores cenários. A suprema e extenuante circunstância é quando um dos procedimentos acarreta o risco de morte ou incapacidade. O valor esperado pode ajudar a organizar essa informação também.

Riscos de um modo ou de outro

Em algum momento de sua vida, é provável que lhe caiba tomar decisões cruciais sobre sua saúde ou a de alguém que você preza. O que torna tudo mais difícil é que a situação provavelmente provocará estresse físico e psicológico, o que reduzirá a precisão de sua capacidade decisória. Se você perguntar ao médico sobre a exatidão dos exames, ele talvez não saiba. Se procurar pesquisar as chances de diversos tratamentos, talvez descubra que seu médico está mal preparado para percorrer as estatísticas.26 Os médicos são evidentemente essenciais para o diagnóstico da doença, para apresentar as várias opções de tratamento, tratar o paciente e acompanhar o tratamento a fim de verificar se está sendo eficaz. Mesmo assim, como afirmou um médico, “os médicos conseguem transmitir melhor o que conhecem sobre a eficácia do que sobre o risco, e isso distorce a tomada de decisão”.27 Além disso, as pesquisas focam no sucesso ou insucesso da intervenção, e a questão dos efeitos colaterais se revela menos interessante para quem criou a pesquisa. Os médicos se instruem sobre o sucesso dos procedimentos, mas nem tanto sobre os insucessos — isso cabe a você, como mais uma forma de trabalho paralelo.

Veja as cirurgias de ponte de safena — são 500 mil realizadas todo ano nos Estados Unidos.28 Qual a evidência da sua utilidade? Pesquisas clínicas aleatórias não revelam nenhum benefício à sobrevivência da maioria dos pacientes que se submeteu ao procedimento.29 Mas os cirurgiões não se convenceram porque a lógica do procedimento já lhes bastava como justificativa. “Você tem um vaso entupido, você contorna o entupimento, conserta o problema, fim de papo.” Se os médicos acham que um tratamento deve funcionar, eles acabam acreditando que de fato funciona, mesmo quando a evidência clínica é inexistente.30

A angioplastia foi de zero a 100 mil procedimentos por ano sem testes clínicos31 — como a cirurgia de ponte de safena, sua popularidade baseou-se apenas na lógica do procedimento, mas os testes clínicos não demonstram benefício em termos de sobrevivência.32 Alguns médicos dizem a seus pacientes que a angioplastia irá aumentar sua expectativa de vida em dez anos, mas, para aqueles que têm uma doença coronariana estabilizada, ela não demonstrou aumentar sua expectativa de vida em um dia sequer.33

Esses pacientes eram todos tolos? De modo algum. Mas estavam vulneráveis. Quando um médico nos diz “Você está com uma enfermidade que pode matar, mas eu tenho um tratamento que funciona”, é natural que nos entreguemos a essa chance. Fazemos perguntas — mas não em demasia —, queremos que nos devolvam nossa vida, e estamos dispostos a seguir as ordens do médico. Há uma tendência a suprimirmos nossos próprios processos de tomada de decisão quando nos sentimos arrasados, algo que já se demonstrou experimentalmente. As pessoas que recebem uma opção junto com a opinião de um especialista param de usar as partes do cérebro que controlam a tomada de decisão independente e entregam essa decisão ao especialista.34,35

Por outro lado, a expectativa de vida não é toda a história, mesmo sendo dessa maneira que muitos cardiologistas vendam as pontes e a angioplastia a seus pacientes. Muitos pacientes relatam uma melhoria dramática na qualidade de vida depois desses procedimentos, na capacidade de fazer aquilo que amam. Podem não viver mais, mas vivem melhor. Esse é um fator crucial em qualquer opção médica, que não pode ser varrido para debaixo do tapete. Pergunte a seu médico não apenas sobre a eficácia e a mortalidade, mas sobre a qualidade de vida e efeitos colaterais que possam incidir fortemente sobre ela. Na verdade, muitos pacientes dão mais valor à qualidade de vida do que à longevidade, e estão dispostos a trocar esta última pela primeira.

Um forte exemplo das ciladas implicadas no processo decisório médico nos vem do estado atual do tratamento do câncer de próstata.36 Estima-se que 2,5 milhões de homens nos Estados Unidos tenham câncer de próstata,37 e que 3% morrerão disso.38 A doença não figura entre as dez maiores causas de morte, mas é a segunda causa de morte entre os homens, depois do câncer de pulmão. Quase todo urologista que dá a notícia recomenda a remoção cirúrgica radical da próstata.39 E, à primeira vista, parece algo razoável — descobrimos o câncer, nos livramos dele.

Várias coisas tornam complicado pensar sobre o câncer de próstata. Primeiro, é um câncer de evolução especialmente lenta — a maioria dos homens morre com ele, e não por causa dele.40 Ainda assim, a palavra terrível que começa com c provoca tanto medo e intimidação que muitos homens querem apenas “se livrar dele e resolver o problema”. Estão dispostos a suportar os efeitos colaterais para ter certeza de que o câncer sumiu. Mas, veja só, há um alto grau de reincidência após a cirurgia. E os efeitos colaterais?41 A taxa de incidência — a frequência com que se manifestam os efeitos colaterais depois da cirurgia — está entre parênteses:

• incapacidade de manter uma ereção suficiente para a relação sexual (80%)
• encurtamento do pênis em até 2,5 centímetros (50%)
• incontinência urinária (35%)
• incontinência fecal (25%)
• hérnia (17%)
• corte da uretra (6%)

Os efeitos colaterais são terríveis. A maioria das pessoas diria que são melhores que a morte, que elas creem ser a alternativa à cirurgia. Mas os números nos contam uma história diferente. Primeiro, uma vez que o câncer de próstata é de lenta evolução e assintomático na maioria das pessoas que sofre dele, ele pode seguramente passar sem tratamento em alguns homens. Quantos? Um total de 47 em 48.42 Em outras palavras, para cada 48 cirurgias da próstata realizadas, apenas uma vida é prolongada — os outros 47 pacientes teriam vivido a mesma quantidade de tempo, de qualquer maneira, sem sofrer os efeitos colaterais. Assim, o número de pessoas a tratar para se conseguir uma cura é 48. Agora, quanto aos efeitos colaterais, há a chance de mais de 97% de o paciente sofrer de pelo menos um dos que acabei de listar. Se ignorarmos os efeitos colaterais sexuais — os dois primeiros — e olharmos apenas os outros, ainda assim há a chance de 50% de que o paciente sofra pelo menos um deles, e bastante chance de sofrer dois. Então, das 47 pessoas que não se beneficiaram da cirurgia, mais ou menos 24 irão sofrer pelo menos um efeito colateral. Recapitulando: para cada 48 cirurgias de próstata realizadas, 24 pessoas que estariam bem sem a cirurgia sofrem um grande efeito colateral, enquanto 1 pessoa é curada. Você está 24 vezes mais propenso a ser lesado pelos efeitos colaterais do que ajudado por uma cura.43 Dos homens que passam pela cirurgia, 20% se arrependem da decisão.44 Evidentemente, é preciso computar o fator qualidade de vida na decisão.

Então por que quase todo urologista recomenda a cirurgia? Para começo de conversa, o procedimento cirúrgico é um dos mais complicados e difíceis que se conhece. É de pensar que esse seria um motivo para não ser recomendado, mas é preciso considerar que os médicos investiram muito para aprender a técnica. O treino para realizar a operação é enorme, e aqueles que dominaram a técnica são valorizados por essa rara capacidade. Além disso, os pacientes e suas famílias esperam que o médico faça alguma coisa. Os pacientes tendem a ficar insatisfeitos com médicos que dizem “Vamos continuar observando”. As pessoas que procuram um médico por causa de uma gripe ficam evidentemente aborrecidas quando saem do consultório de mãos vazias, sem uma receita. Várias pesquisas demonstram que esses pacientes acham que o médico não os levou a sério, não foi cuidadoso ou ambos.

Outro motivo de a cirurgia ser imposta é que o objetivo do cirurgião é erradicar o câncer com a menor incidência possível de uma recidiva. Os pacientes são cúmplices neste aspecto: “É muito difícil dizer a um cirurgião para deixar o câncer intocado”, explica o dr. Jonathan Simons, presidente da Prostate Cancer Foundation.45 As faculdades de medicina ensinam que a cirurgia é a regra de ouro para a maioria dos cânceres, com índices de sobrevivência superiores a outros métodos, e muito mais altos do que quando se ignora o problema. Elas usam uma estatística sumária de quantas pessoas morreram de câncer tratado cinco a dez anos depois da cirurgia. Mas esse sumário ignora outros dados importantes, como a suscetibilidade a outras doenças, a qualidade de vida após a cirurgia e o tempo de recuperação.

O dr. Barney Kenet, um dermatologista de Manhattan, acha tudo isso fascinante. “Ensinam aos cirurgiões que ‘uma chance de cortar é uma chance de curar’”, diz ele. “Faz parte do DNA. Nos exemplos que você me deu sobre o câncer, com as probabilidades e estatísticas cuidadosamente analisadas, a ciência de tratar colide com a arte da prática médica — e trata-se de uma arte.”46

As faculdades de medicina e os cirurgiões talvez não se preocupem tanto com a qualidade de vida, mas você deveria se preocupar. Grande parte da tomada de decisão médica gira em torno de sua própria disposição de correr riscos e o seu limite de tolerância com inconvenientes, dor e efeitos colaterais. Quanto do seu tempo você está disposto a passar no consultório médico, preocupando-se com resultados? Não existem respostas fáceis, mas as estatísticas podem ajudar bastante a clarear essas questões. Voltando às cirurgias da próstata, o período de recuperação aconselhável é de seis semanas — não parece ser um período absurdo de tempo, considerando que a cirurgia pode salvar sua vida.

Mas a pergunta a fazer não é “Estou disposto a investir seis semanas para salvar a minha vida?”, mas “Minha vida está sendo realmente salva? Serei uma das 47 pessoas que não precisam da cirurgia ou uma das que precisam?”. Embora não dê para saber a resposta, faz sentido se apoiar nas probabilidades para guiar sua decisão; é estatisticamente improvável que você seja beneficiado pela cirurgia, a não ser que tenha uma informação específica sobre a agressividade de seu câncer. Eis uma informação adicional capaz de jogar um foco preciso sobre a decisão: a cirurgia aumenta a vida do homem, em média, em seis semanas. Esse número é derivado da média das 47 pessoas cujas vidas não foram em nada aumentadas (algumas foram abreviadas por complicações cirúrgicas), e a única pessoa cuja vida foi salva pela cirurgia ganhou cinco anos e meio. O aumento de seis semanas da vida é exatamente igual ao período de seis semanas de recuperação! A decisão pode ser então enquadrada assim: você quer passar essas seis semanas agora, enquanto é jovem e saudável, deitado na cama se recuperando de uma cirurgia de que você provavelmente não precisava? Ou prefere tirar essas seis semanas do final de sua vida, quando será mais velho e menos ativo?

Muitos procedimentos cirúrgicos e regimes de tratamento apresentam exatamente esta troca: o período do tempo de recuperação pode igualar ou exceder o período de vida que você está ganhando. A evidência sobre os benefícios do ganho de vida provocado pelo exercício é semelhante. Não me interprete mal — o exercício gera muitos benefícios, inclusive melhora do ânimo, fortalecimento do sistema imunológico e melhora do tônus muscular (e, portanto, da aparência geral). Algumas pesquisas demonstram que ele chega a melhorar a clareza do raciocínio através da oxigenação do sangue. Mas examinemos uma afirmação que atraiu muita atenção no noticiário: a de que se você fizer uma hora diária de exercícios aeróbicos e alcançar a meta de seu ritmo cardíaco, prolongará sua expectativa de vida. Parece bom, mas até que ponto? Algumas pesquisas revelam que você aumenta a extensão da sua vida em uma hora por cada hora de exercício.47 Se você adora se exercitar, isso é um grande negócio — você está fazendo algo de que gosta e ainda por cima ganhando tempo de vida na mesma proporção. Seria como dizer que cada hora que você passa em meio a atividades se­xuais, ou tomando sorvete, prolonga sua vida em uma hora. A escolha é fácil — a hora que você passa se exercitando é essencialmente “livre”, e não conta entre as horas com que você foi contemplado nesta vida. Mas se você detesta fazer exercícios e os acha desagradáveis, a hora que passa realizando-os conta como uma hora perdida. Há enormes benefícios no exercício diário, mas aumentar seus dias de vida não é um deles. Isto não é motivo para não se exercitar — mas é importante que se tenha expectativas razoáveis quanto aos resultados.

Há duas objeções frequentes a essa linha de pensamento. A primeira é que falar sobre estatísticas em uma decisão de vida ou morte como essa não faz sentido porque nenhum paciente real de cirurgia de próstata tem sua vida aumentada pela média citada de seis semanas. Uma pessoa tem sua vida prolongada em cinco anos e meio, e 47 em nem um dia sequer. Esse aumento “médio” de seis semanas é simplesmente uma ficção estatística, como o exemplo sobre o estacionamento.

É verdade que ninguém ganha esse período; a média muitas vezes não é uma quantidade que se aplica a uma única pessoa.48 Mas isso não invalida o raciocínio por trás dela, o que leva à segunda objeção: “Não se pode avaliar essa decisão do mesmo modo que se calculam caras e coroas e jogos de cartas, com base em probabilidades. As probabilidades e valores esperados só são significativos num universo de muitas tentativas e resultados”. Mas a maneira racional de encarar essas decisões não é encará-las como “algo singular”, completamente separado do tempo e da experiência de vida, e sim como parte de uma série de decisões que você precisará tomar no decorrer de sua vida. Embora cada decisão individual seja singular, somos confrontados por problemas durante toda a vida, cada um acarretando uma probabilidade e um valor esperado. Você não está tomando uma decisão sobre esse procedimento cirúrgico isolada de outras decisões na sua vida. Você a está tomando no contexto de milhares de decisões, como ingerir vitaminas, se exercitar, usar fio dental após cada refeição, tomar vacina contra gripe, fazer uma biópsia. A tomada de decisão estritamente racional nos diz para prestar atenção ao valor esperado de cada decisão.

Cada decisão acarreta incerteza e riscos, muitas vezes se barganha tempo e conveniência agora por algum resultado desconhecido no futuro. É claro que você usaria o fio dental depois de toda refeição se estivesse 100% convencido de que com isso gozaria de perfeita saúde bucal. Você espera isso ao usar o fio dental com tanta frequência? A maioria de nós não está convencida, e usar o fio dental três vezes por dia (e também depois de lanches) parece ser mais um problema que não vale a pena.

Obter estatísticas precisas pode parecer fácil, mas muitas vezes não é. Veja as biópsias, que são corriqueiras e feitas como rotina, acarretando riscos mal compreendidos até por muitos cirurgiões que as fazem. Na ­biópsia, uma pequena agulha é enfiada no tecido, e uma amostra desse tecido é retirada para análise posterior por um patologista, que procura observar se as células são cancerosas ou não. O procedimento em si não é uma ciência exata — não é como num episódio de CSI, quando um técnico põe uma amostra num computador e obtém a resposta em outra tela.

A análise da biópsia envolve a avaliação humana e o equivalente a um exame do tipo “parece esquisito?”. O patologista ou histologista examina a amostra ao microscópio e repara em quaisquer regiões que, a seu ver, não sejam normais. Ele então conta o número de regiões e as considera uma proporção de toda a amostra. O relatório do patologista pode conter algo como “5% da amostra têm células anormais” ou “nota-se carcinoma em 50% da amostra”. Dois patologistas muitas vezes discordam sobre a análise, e chegam a assinalar dois graus de câncer para a mesma amostra. É por isso que é importante obter uma segunda opinião sobre a sua biópsia — você não deve começar a planejar uma cirurgia, quimioterapia ou tratamento radioativo até ter certeza absoluta de que precisará deles. Nem deve ser muito displicente sobre o laudo negativo de uma biópsia.

Para nos atermos ao exemplo do câncer de próstata, falei com seis cirurgiões de seis grandes hospitais universitários e perguntei a eles sobre os riscos dos efeitos colaterais da biópsia da próstata. Cinco disseram que o risco de efeitos colaterais da biópsia era por volta de 5%, o mesmo que podemos ler nas revistas de medicina. O sexto disse que não havia risco — isso mesmo, nenhum absolutamente. O efeito colateral mais comum mencionado na literatura é a infecção; o segundo mais comum é o rompimento do reto; e o terceiro, incontinência. Septicemia é perigosa e pode ser fatal. A agulha da biópsia precisa passar pelo reto, e o risco da septicemia vem da contaminação das cavidades da próstata e do abdome com matéria fecal. O risco é normalmente reduzido através da administração de antibióticos ao paciente antes do procedimento, mas, mesmo com essa precaução, ainda resta o risco de 5% de efeitos colaterais indesejáveis.

Nenhum dos médicos que consultei quis falar sobre o período de recuperação da biópsia, ou daquilo que chamaram eufemisticamente de efeitos colaterais “inconvenientes”. Não ameaçam a saúde, são apenas desagradáveis. Foi só quando mencionei uma pesquisa de 2008 na revista Urology que eles admitiram que, um mês depois da biópsia, 41% dos homens tiveram disfunção erétil e, seis meses depois, 15%.49 Outros efeitos colaterais “inconvenientes” incluem diarreia, hemorroidas, mal-estar gastrointestinal e sangue no esperma, que pode durar vários meses. Dois médicos admitiram a contragosto que haviam retido essa informação. Como afirmou um deles, “não mencionamos essas complicações aos pacientes para não desencorajá-los a fazer a biópsia, um procedimento muito importante”. É esse tipo de paternalismo da parte dos médicos que desagrada muita gente, e que também viola o princípio fundamental de consentimento após informação.

Ora, um risco de 5% de efeitos colaterais pode não parecer tão grave, mas pense nisto: muitos homens que receberam um diagnóstico de câncer de próstata em estágio inicial ou grau pouco agressivo optaram por conviver com ele e monitorá-lo, um plano conhecido como espera monitorada ou vigilância ativa. Na vigilância ativa, o urologista pode pedir biópsias a intervalos regulares, talvez a cada doze ou 24 meses. Para uma doença lenta que pode levar mais de uma década para revelar sintomas, isso significa que alguns pacientes passarão por cinco ou mais biópsias. Qual é o risco de septicemia ou algum outro efeito colateral sério durante uma ou mais biópsias se você faz cinco biópsias, cada qual acarretando o risco de 5%?

Esse cálculo não segue a regra de multiplicação mostrada antes; só poderíamos usá-la se quiséssemos saber a probabilidade de um efeito colateral em todas as cinco biópsias — como tirar cara cinco vezes consecutivas. E não exige uma tabela quádrupla porque não estamos fazendo uma pergunta bayesiana, como “Qual a probabilidade de eu ter câncer, considerando que a biópsia foi positiva?” (os patologistas às vezes erram — é o equivalente aos exames de sangue que vimos antes). Para perguntar sobre o risco de um efeito colateral em pelo menos uma de cinco biópsias — ou perguntar sobre a probabilidade de tirar cara pelo menos uma vez em cinco jogadas de moeda — precisamos usar algo chamado binômio de Newton. O binômio de Newton pode dizer a probabilidade de o mau evento acontecer pelo menos uma vez, todas as cinco vezes ou quantas você quiser. Se pararmos para pensar nisso, a estatística mais útil num caso assim não é a probabilidade de você ter um efeito colateral adverso exatamente uma vez nas cinco biópsias (de qualquer forma, nós já sabemos como calcular isso, usando a regra de multiplicação). O que você deseja saber é a probabilidade de sofrer um efeito adverso ao menos uma vez, isto é, em uma ou mais biópsias. As probabilidades são diferentes.

Aqui o mais fácil é usar as muitas calculadoras disponíveis on-line, como esta: <http://www.stat.tamu.edu/~west/applets/normaldemo.html>.

Para usá-la, preencha a seguinte informação nos campos na tela:

n se refere ao número de vezes que você vai passar pelo procedimento (na linguagem estatística, são as “tentativas”).

p se refere à probabilidade de um efeito colateral (na linguagem da estatística, são os “eventos”).

x se refere a quantas vezes ocorre o evento.

Usando o exemplo, estamos interessados em saber a probabilidade de acontecer ao menos um resultado ruim (o evento) se você fizer a biópsia cinco vezes. Logo,

n = 5 (5 biópsias)

p = 5%, ou 0,05

x = 1 (1 mau resultado)

Alimentando a calculadora binomial com esses números, vemos que se você faz cinco biópsias, a probabilidade de ter um efeito colateral é de 23%.

Dos cinco cirurgiões que admitiram a probabilidade de 5% de haver um efeito colateral da biópsia prostática, só um compreendeu que o risco aumentava a cada biópsia. Três deles disseram que o risco de 5% se aplicava a uma vida inteira de biópsias — você pode fazer quantas quiser, que o risco não aumenta nunca.

Expliquei que cada biópsia representava um evento independente, e que duas biópsias representavam um risco maior do que uma. Nenhum deles aceitou isso. A primeira das minhas conversas foi assim:

“Li que o risco de complicações sérias da biópsia é de 5%.”

“Está certo.”

“Então, se um paciente faz cinco biópsias, isso aumenta o risco para quase 25%.”

“Você não pode simplesmente somar as probabilidades.”

“Concordo que não. É preciso usar o binômio de Newton, e aí se chega ao resultado de 23% — bastante próximo de 25%.”

“Nunca ouvi falar de binômio de Newton, e tenho certeza de que não se aplica aqui. Não espero que você entenda isto. É necessária uma formação estatística.”

“Bem, eu tive formação estatística. Acho que consigo compreender.”

“O que é mesmo que você faz?”

“Sou pesquisador — neurocientista. Dou aula nos nossos cursos de graduação em estatística, e já publiquei alguns estudos sobre métodos estatísticos.”

“Mas você não é médico formado, como eu. Seu problema é que não entende de medicina. Sabe, as estatísticas médicas são diferentes de outras estatísticas.”50

“O quê?”

“Tenho vinte anos de experiência médica. Quantos você tem? Estou lidando com o mundo real. Você pode adotar as teorias que quiser, mas não sabe nada. Eu vejo pacientes o dia inteiro. Sei o que estou vendo.”

Outro cirurgião, um perito mundial em cirurgia guiada pelo “robô” Vinci, me disse: “Essas estatísticas não me parecem estar certas. Já devo ter feito umas quinhentas biópsias e acho que nunca vi mais de umas duas dezenas de casos de septicemia em toda a minha carreira”.

“Bem, 24 de quinhentas é mais ou menos 5%.”

“Bem, tenho certeza de que não foram tantas assim. Eu teria notado se fossem 5%.”

Guiado pelo masoquismo, ou otimismo, fui ver o chefe do departamento de oncologia de outro importante hospital. Se alguém tiver câncer de próstata, frisei, é melhor não fazer cirurgia por causa do número de pessoas a tratar: somente 2% dos pacientes irão se beneficiar do tratamento.

“Imagine se fosse você o diagnosticado”, disse ele. “Você não iria querer deixar de fazer a cirurgia! E se você estivesse dentro desses 2%?”

“Bem, eu provavelmente não estaria.”

“Mas você não sabe.”

“Tem razão, eu não sei, mas, por definição, é improvável — só há uma chance de 2% de que eu estivesse dentro dos 2%.”

“Mas você não sabe que não está. E se estivesse? Então iria querer a cirurgia. Qual o seu problema?”

Discuti tudo isso com o chefe da oncologia urológica de outro hospital universitário, um pesquisador clínico que publica artigos sobre câncer de próstata em revistas científicas, e cujos estudos são dotados de um domínio profissional de estatística. Ele pareceu decepcionado, ainda que não surpreso, com as histórias de seus colegas. Explicou que parte do problema do câncer de próstata é que o exame geralmente usado para detectá-lo, o PSA [Prova do Antígeno Prostático], é mal compreendido, e que os dados não batem com sua eficácia em prever resultados. As biópsias também são problemáticas porque dependem de amostras da próstata, e é mais fácil extrair amostras de certas regiões que de outras. Finalmente, explicou, os exames de imagem são promissores — a ressonância magnética e a ultrassonografia, por exemplo —, mas há ainda poucos estudos de longo prazo para concluir algo sobre sua eficácia na previsão dos resultados. Em alguns casos, nem mesmo a ressonância magnética de alta resolução é capaz de detectar dois terços dos cânceres que aparecem nas biópsias. De qualquer forma, as ­biópsias para o diagnóstico e a cirurgia e radiação como tratamento ainda são tidas como o padrão de ouro para resolver o câncer de próstata. Os médicos são treinados para tratar os pacientes e para usar técnicas eficazes, mas geralmente carecem de instrução em raciocínio científico ou probabilístico — você mesmo precisa aplicar esse raciocínio, idealmente em conjunto com seu médico.

O que os médicos têm a oferecer

Mas espere um momento — se os médicos raciocinam tão mal, como a medicina alivia tantas dores e prolonga tantas vidas? Eu me concentrei em alguns casos de destaque — câncer de próstata, procedimentos cardíacos — nos quais a medicina está num estado de fluxo. E foquei o tipo de problema notoriamente difícil, que implica deficiências cognitivas. Mas existem muitos sucessos: a imunização, o tratamento da infecção, transplantes de órgãos, cuidados preventivos e a neurocirurgia (como a de Salvatore Iaconesi, no Capítulo 4), para citar apenas alguns.

O fato é que se há algo errado com você, você não corre para os livros de estatística, vai a um médico. A prática da medicina é tanto uma arte quanto uma ciência.51 Alguns médicos aplicam inferências bayesianas sem saber o que estão realmente fazendo. Usam seu treinamento e seus poderes de observação para identificar padrões — sabendo quando um paciente se encaixa num padrão específico de sintomas e fatores de risco para poder fazer um diagnóstico e um prognóstico.

Como diz Scott Grafton, um importante neurologista na UC Santa Barbara, “a experiência e o conhecimento implícito realmente importam. Recentemente fiz uma ronda clínica com dois médicos da emergência que tinham, somados, cinquenta anos de experiência clínica. Havia zero em matéria de ginástica verbal e lógica formal do tipo que Kahneman e Tversky ostentam. Eles simplesmente reconhecem um problema. Adquiriram perícia através de um extremo aprendizado de reforço, tornaram-se sistemas excepcionais de reconhecimento de padrões. Essa aplicação de reconhecimento de padrão é fácil de compreender num radiologista que examina radiografias. Mas também vale para qualquer grande clínico. Eles podem gerar probabilidades bayesianas extremamente precisas com base na experiência de anos, combinadas com o bom uso de exames, um exame físico e o histórico do próprio paciente”. Um bom médico terá tido contato com milhares de casos que formam uma rica história estatística (os bayesianos chamam isso de distribuição a priori) sobre a qual podem erigir uma crença em torno do paciente. Um grande médico empregará tudo isso sem esforço, e chegará a uma conclusão que resultará no melhor tratamento para o paciente.

“O problema com argumentos heurísticos e bayesianos”, continuou Grafton, “é que eles não conseguem reconhecer que muita coisa que o médico aprende a fazer é extrair a informação diretamente do paciente, e individualizar a tomada de decisão a partir disso. É de uma extrema eficácia. Um bom médico pode entrar no quarto de um hospital e cheirar a morte iminente.” Quando muitos médicos entram numa UTI, por exemplo, eles olham para os sinais vitais e para o relatório. Quando Grafton entra na UTI, ele olha para o paciente, utilizando sua capacidade essencialmente humana para compreender o estado físico e mental de outra pessoa.

Os bons médicos falam com seus pacientes para compreender a história e os sintomas. Usam com elegância a identificação de padrões. A ­ciência informa seus julgamentos, mas eles não dependem de nenhum exame em especial. Nos casos dos dois venenos e da visão embaçada, passei por cima de um fato importante sobre como as verdadeiras decisões médicas são tomadas. Seu médico não teria pedido o exame se não achasse, com base no exame pessoal que fez em você e no seu histórico, que você poderia ter a doença. Para minha visão embaçada inventada, apesar da incidência básica na população em geral ser de 1 em 38 mil, não é essa a incidência básica da doença para as pessoas que têm visão embaçada, acabam no consultório médico e, no final, fazem um exame. Se essa incidência de base é, digamos, 1 em 9500, você pode refazer a tabela e descobrir que a chance de contrair visão embaçada aumenta de 1 em 201 para cerca de 1 em 20. É disso que se trata a atualização bayesiana — encontrar estatísticas relevantes para sua circunstância particular e usá-las. Você melhora suas estimativas de probabilidade restringindo o problema a um conjunto de pessoas que se parece mais com você no âmbito de dimensões pertinentes. A pergunta não é “Qual a probabilidade de eu ter um derrame?”, por exemplo, e sim “Qual a probabilidade de alguém de idade, gênero, pressão sanguínea e nível de colesterol iguais aos meus ter um derrame?”. Isso envolve a combinação da ciência da medicina com a arte da medicina.

E apesar de haver coisas em que não é tão boa, é difícil contestar os êxitos esmagadores da medicina no decorrer dos últimos cem anos. Os Centros de Controle e Prevenção a Doenças em Atlanta relatam a erradicação quase completa — um declínio de 99% em morbidez —, entre 1900 e 1998, de nove doenças que antes matavam centenas de milhares de americanos: varíola, difteria, tétano, sarampo, caxumba, rubéola, Haemophilus influenzae, coqueluche e pólio. A difteria caiu de 175 mil casos para 1;52 o sarampo, de 500 mil para cerca de 90. Durante a maior parte da história humana, desde aproximadamente 10 mil a.C. até 1820, nossa expectativa de vida era de cerca de 25 anos. A expectativa mundial cresceu para mais de sessenta anos,53 e, desde 1979, a expectativa de vida nos Estados Unidos aumentou de 71 para 79 anos.54

Que dizer dos casos em que os médicos estão mais diretamente envolvidos com os pacientes? Afinal, a longevidade pode ser atribuída a outros fatores, como melhorias de higiene. No campo de batalha, mesmo que as armas façam maiores estragos, a chance de o soldado ferido ser tratado com êxito aumentou dramaticamente: no decorrer da Guerra Civil Americana e das duas guerras mundiais, a chance de morrer por ferimento era de 1 em 2,5; durante a guerra no Iraque, havia diminuído para 1 em 8,2. As taxas de mortalidade infantis, neonatais e pós-neonatais também diminuíram.55 Em 1915, para cada mil nascimentos, cem crianças morriam antes de seu primeiro ano; em 2011, esse número havia diminuído para quinze. E apesar de o câncer de próstata, do seio e do pâncreas continuarem sendo desafios especialmente difíceis, as taxas de sobrevivência aumentaram de quase 0% em 1950 para 80% hoje.56

É evidente que a medicina está fazendo muita coisa certa, e também a ciência por trás dela. Mas resta uma região sombria e cinzenta de pseudomedicina, que é problemática porque tolda o juízo de pessoas que necessitam de um verdadeiro tratamento médico, e também porque é desorganizada.

Medicina alternativa: uma violação do consentimento informado

Um dos princípios fundamentais da medicina moderna é o consentimento informado — o fato de você ter sido completamente esclarecido sobre todos os prós e contras de qualquer tratamento a que vai se submeter, de que recebeu toda a informação disponível de modo a poder tomar uma decisão esclarecida.

Infelizmente, o consentimento informado não é praticado de fato na moderna prática de saúde. Somos bombardeados por informações, a maioria incompletas, distorcidas ou equivocadas, e no momento em que estamos menos emocionalmente preparados para lidar com isso. Isso é especialmente verdade com a medicina alternativa e as terapias alternativas.

Um número crescente de indivíduos busca alternativas aos sistemas médico-hospitalares profissionais para tratar das enfermidades. Como a indústria não é regulamentada, é difícil chegar aos números, mas a Economist calcula que seja um negócio de 60 bilhões de dólares no mundo todo.57 Cerca de 40% dos americanos relatam o uso de medicamentos e terapias alternativas, que incluem preparações homeopáticas e herbais, práticas de cura espiritual e psíquica, e diversas manipulações não médicas do corpo e da mente com intuitos curativos.58 Considerando sua proeminência em nossas vidas, existem informações básicas que todo mundo que consente nestes tratamentos de saúde deveria ter.

A medicina alternativa é simplesmente uma medicina que não tem provas de sua eficácia. Depois que se demonstrou cientificamente a eficácia de um tratamento, ele não é mais chamado de alternativo — é simplesmente chamado de medicina.59 Antes que um tratamento faça parte da medicina convencional, ele passa por uma série de experiências controladas para se obterem provas de que é seguro e eficaz. Para que seja considerado medicina alternativa, não se exige nada disso. Se alguém acredita na eficácia de determinada intervenção, ela se torna “alternativa”. O consentimento esclarecido significa que devemos receber informação sobre a eficácia do tratamento e quaisquer riscos potenciais, e é isso que falta à medicina alternativa.

Justiça seja feita, dizer que não há provas não quer dizer que o tratamento seja ineficaz; simplesmente que sua eficácia ainda não foi demonstrada — estamos numa condição agnóstica. Mas o próprio nome “medicina alternativa” é enganoso. É alternativa, mas não é medicina (alternativa a quê, então?).

Em que a ciência difere da pseudociência? A pseudociência muitas vezes usa a terminologia e a observação da ciência, mas não todo o rigor das experiências controladas e das hipóteses falseáveis. Um bom exemplo é a medicina homeopática, uma prática do século XIX que acarreta a administração de doses minúsculas (ou, de fato, uma dose inexistente) de substâncias inofensivas que pretensamente promovem a cura. Baseia-se em duas crenças. Primeiro, quando a pessoa demonstra sintomas como insônia, problemas estomacais, febre, tosse ou tremores, a administração de alguma substância que em dose normal causaria esses problemas é capaz de curá-los. Não existe nenhum fundamento científico para essa alegação. Se você está intoxicado por hera venenosa e eu lhe der mais hera venenosa, a única coisa que fiz foi lhe dar mais hera venenosa. Não é a cura — é o problema! A segunda crença é a de que a diluição repetida de uma substância pode deixar resíduos da substância original que são ativos e possuem propriedades curativas, e que quanto mais diluída for a substância, mais potente e eficaz será.60 De acordo com os homeopatas, as “vibrações” da substância original deixam impressões nas moléculas da água.61

E a diluição precisa ser feita segundo um procedimento muito específico.62 Um homeopata pega uma parte da substância química e a dilui em dez partes de água; em seguida, agita-a dez vezes para cima e para baixo e dez vezes de um lado para outro. Então, ele pega uma parte desta solução e a dilui em dez partes de água, e sacode tudo de novo. Ele faz isso pelo menos vinte vezes, o que resulta numa solução em que há uma parte da substância original para 100 quintilhões de partes de água. Para os produtos homeopáticos no varejo, as diluições são rotineiramente de 1 seguido de 30 zeros, e muitas vezes 1 seguido de — vejam só — 1500 zeros. Isso equivale a pegar um grão de arroz, amassá-lo até virar pó, e dissolvê-lo numa esfera de água do tamanho de nosso sistema solar.63 Ah, esqueci: e então repetir esse processo 26 vezes. A homeopatia foi inventada antes que o cientista Amedeo Avogadro descobrisse uma constante matemática que hoje leva seu nome, e que exprime a quantidade de átomos ou moléculas que são retidos numa diluição (6,02 × 1023). A questão é que nas diluições padronizadas da homeopatia de varejo não resta nada da substância original. Mas isso é suspostamente bom, porque, é preciso lembrar, quanto mais diluído o remédio homeopático, mais potente ele é. Tudo isso levou o cético profissional James Randi a observar que a maneira de tomar uma overdose de um remédio homeopático é simplesmente não tomá-lo. (Randi ofereceu 1 milhão de dólares durante mais de uma década para qualquer um que conseguisse comprovar que a homeopatia funcionava.)64

A homeopatia é uma pseudociência porque (a) não se sustenta diante de experiências controladas, (b) usa linguagem científica, como diluição e molécula, e (c) não faz sentido dentro de uma compreensão científica de causa e efeito.

Pondo de lado a homeopatia, quando se trata de uma doença séria como câncer, infecção, doença de Parkinson, pneumonia, ou mesmo ­doenças mais leves como resfriados comuns e gripes, não há evidência de que a medicina alternativa seja eficaz. Edzard Ernst, um pesquisador britânico, analisou centenas de pesquisas e descobriu que 95% dos tratamentos eram indistinguíveis de nenhum tratamento — ou seja, eram equivalentes a um placebo.65 (Os outros 5% que funcionam podem representar um erro da experiência, de acordo com a margem tradicional de acerto na pesquisa científica.) As vitaminas e os suplementos não se saem melhor. Depois de extensas pesquisas clínicas conduzidas no decorrer de décadas por muitos laboratórios de pesquisa diferentes, segundo diversos protocolos, descobriu-se que os polivitamínicos não servem para nada.66 Na verdade, as vitaminas podem fazer mal. Nas doses contidas nos comprimidos de vitamina, a vitamina E e o ácido fólico foram associados a um risco aumentado de câncer. O excesso de vitamina D foi associado a um maior risco de inflamação cardíaca,67 e o excesso de vitamina B6, associado a danos nos nervos.68 Nas quantidades de uma dieta normal, essas vitaminas não representam um problema, mas as quantidades tipicamente encontradas nos suplementos e comprimidos de vitaminas vendidos no balcão podem fazer mal. E apesar de milhões de americanos tomarem vitamina C69 ou echinacea70 quando acham que estão ficando gripados, há pouca evidência de que elas funcionem. Por que acreditamos no contrário?

A parte frontal de nossos cérebros se desenvolveu para notar a ocorrência simultânea dos eventos, mas não a falta de ocorrência. Isto tem a ver com as tabelas quádruplas que examinamos antes: nossos cérebros tendem automaticamente para o que existe na célula superior esquerda — o que os psicólogos chamam de correlação ilusória.

A correlação é ilusória porque a célula superior esquerda não nos revela tudo de que precisamos para chegar à melhor conclusão. Imagine que você sinta a chegada de um resfriado e comece a tomar echinacea. Você nota que o resfriado não evolui. Isso lhe acontece cinco vezes, então você conclui que a echinacea ajudou. Sua tabela quádrupla parece algo assim:

Muito impressionante! Eis alguns problemas. Certos resfriados desaparecem mesmo que você não faça nada. E pode ter havido vezes em que você sentiu a chegada de um resfriado, não fez nada e prontamente se esqueceu disso. Se você participasse de uma pesquisa científica, haveria uma coleta mais meticulosa de dados do que aquela que nós mesmos fazemos. Eis como o resto da tabela poderia parecer se você a preenchesse como parte de uma pesquisa:

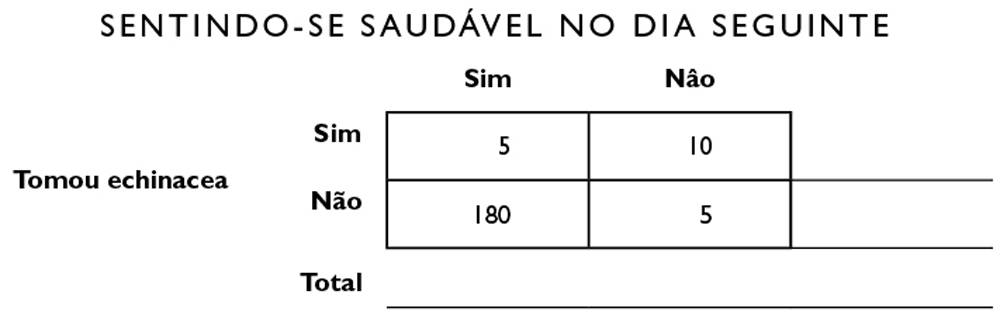
Repare que, para ter um quadro completo, você precisa saber por quantos dias não tomou a echinacea e não pegou um resfriado — isso foi durante a maior parte do tempo! A necessidade de saber isso parece contraintuitiva — mas é exatamente esta a questão: a parte frontal do nosso cérebro tem dificuldade em extrair sentido desse tipo de informação. Basta olhar para a tabela para ver que um resfriado tem o dobro de chance de se desenvolver, quer você tome a echinacea ou não (coluna direita da tabela). Pondo a questão na forma bayesiana, a probabilidade de pegar um resfriado, considerando que você tomou a echinacea, ainda é de 67%.

Aliás, o efeito placebo — através do qual nos sentimos melhor e muitas vezes ficamos melhor apenas tomando qualquer coisa, mesmo que não contenha ingredientes medicinais — é muito forte e muito real. Comprimidos maiores têm um efeito placebo maior do que comprimidos pequenos. Injeções falsas têm efeito maior do que comprimidos. Grande parte do efeito de produtos com valores medicinais desconhecidos pode ser simplesmente efeito placebo. É por isso que testes duplo-cego, randomizados, de controle clínico são necessários: todo mundo que participa recebe uma pílula, e ninguém sabe quem recebeu o quê. Muitas pessoas que tomam a pílula “vazia” vão melhorar em comparação com pessoas que não receberam nada, mas se o remédio realmente funciona, ele deveria funcionar ainda melhor do que o placebo. É assim que os novos tratamentos são aprovados.

Não são apenas a vitamina C e a echinacea que devastam nosso raciocínio causal. Caímos vítimas de correlações ilusórias o tempo todo. Você já passou pela experiência de estar pensando em alguém, alguém que não vê há muito tempo, e então o telefone toca de repente e... uau! Lá está a pessoa! Antes de concluir apressadamente que se trata de poderes paranormais, você precisa ter conhecimento de três outras peças de informação: quantas vezes você pensa em pessoas que não ligam para você, quantas vezes não pensa em alguém que liga e, finalmente, quantas vezes não pensa em alguém que não liga! Processando tudo isso numa tabela quádrupla, é provável que você descubra que as coincidências ocasionais vívidas são inundadas por eventos dos outros três tipos, donde se conclui que essas correlações são ilusórias.

Nossos cérebros evidentemente evoluíram para focar a célula esquerda superior, os acertos, e não se lembrar de mais nada. Um de meus ex-professores, Paul Slovic, chamou isso de negligência com o denominador. Slovic diz que imaginamos o numerador — o caso trágico sobre o desastre de carro que você viu no noticiário — e não pensamos no denominador — a quantidade esmagadora de viagens de carro que terminam em segurança. A negligência com o denominador se mostra de maneiras muito estranhas. Em uma pesquisa, foi dito às pessoas que uma doença matava 1286 indivíduos em cada 10 mil. Elas acharam isso mais perigoso do que as pessoas a quem se falou sobre uma doença que matava 24,14% da população. Reparem que 1286/10 000 é um pouco menos que 13%. Assim, na verdade, representa mais ou menos metade do perigo. Mas no primeiro caso nos concentramos no numerador, os 1286 indivíduos que serão atingidos pela doença. Talvez imaginemos essa quantidade de gente em leitos de hospitais. No segundo caso, ouvimos 24,14%, e o cérebro tende a tratar isso como uma estatística abstrata que não diz respeito a seres humanos.

A negligência com o denominador leva à tendência ao catastrofismo, a imaginar os piores cenários possíveis sem colocá-los nas suas devidas perspectivas estatísticas. Como escreve Daniel Kahneman, “todo pai que já ficou acordado esperando uma filha adolescente que demora a voltar de uma festa reconhecerá essa sensação. Você pode saber que não há realmente (quase) nada com que se preocupar, mas não consegue deixar de ficar imaginando cenários sinistros”.71

A nitidez com que conseguimos recordar as catástrofes, junto da negligência com o denominador, pode levar a decisões verdadeiramente terríveis. Nos dois meses que se seguiram aos ataques terroristas de 11 de setembro de 2001, havia tantas pessoas com medo de voar nos Estados Unidos que elas começaram a viajar de carro, quando normalmente teriam ido de avião. Não houve desastre de avião em outubro ou novembro, mas as mortes em desastres de automóvel durante este período subiram em relação à média em 2170 indivíduos72. Essas pessoas se concentraram no numerador (quatro horríveis desastres de avião, com 246 pessoas a bordo), mas não no denominador (10 milhões de voos comerciais seguros por ano nos Estados Unidos).73 Como disse um pesquisador, “os terroristas podem atacar duas vezes — primeiro, matando diretamente as pessoas, e, segundo, pelo comportamento perigoso que o medo induz na cabeça das pessoas”.74

Um exemplo disso é que tendemos a exagerar a importância de eventos raros. Kahneman descreve o cenário: imagine que funcionários da inteligência alardeiam que bombardeiros suicidas entraram em duas cidades diferentes e estão prontos para atacar. Uma cidade tem um bombardeiro suicida, a outra tem dois. É lógico que os cidadãos da primeira cidade devem se sentir duas vezes mais seguros. Mas, provavelmente, não se sentem.75 A imagem é tão nítida que o medo é aproximadamente idêntico. Agora, se houvesse cem bombardeiros suicidas, seria outra história, mas a questão é que não somos sensíveis à matemática porque nossos cérebros não foram feitos dessa maneira. Felizmente, nós os treinamos.

Isso nos leva de volta à medicina alternativa e ao fato de que muitas de suas pretensões repousam sobre correlações ilusórias, baseadas na negligência do denominador. A atração da medicina alternativa se deve, pelo menos em parte, ao número crescente de pessoas que desconfiam da “medicina ocidental” e buscam alternativas. Oprimidas pelas imperfeições com que é gerido o moderno sistema de saúde, elas sentem necessidade de se rebelar contra aqueles que nos fornecem drogas caras e nem sempre eficazes. Desconfiam dos grandes lucros das companhias farmacêuticas (e de alguns hospitais) e temem os tratamentos recomendados dentro de uma forte cultura de maximização de lucros — sua preocupação é o medo de que alguns tratamentos sejam prescritos não porque sejam melhores para o paciente, mas porque são melhores para aqueles em posição de obter ganhos financeiros. Infelizmente, notícias recentes têm revelado que isso às vezes é verdade.

Os entusiastas da medicina alternativa também reclamam da atitude arrogante e paternalista de certos médicos (“Eu sei o que é bom para você, não é necessário que você compreenda”), exemplificada pelo oncologista urológico com quem falei, que ficou zangado quando lhe pedi que discutíssemos seu raciocínio estatístico sobre a biópsia. Em um dos hospitais mais importantes dos Estados Unidos, as pacientes com câncer de mama que passam por radioterapia não são informadas sobre a grande probabilidade de sofrerem dolorosas queimaduras pela radiação, evidentemente porque os oncologistas decidiram no lugar da paciente que os benefícios do tratamento compensam a dor e o desconforto que possam provocar. Porém, isso é uma violação do princípio do consentimento informado. Todos os pacientes deveriam receber toda a informação disponível, de modo a decidir por si próprios o que estão dispostos ou não a aceitar.

Outra coisa preocupante é a falta de exatidão entre alguns médicos. Em uma pesquisa, os prognósticos feitos por médicos só tiveram precisão de 20%.76 Em outra pesquisa, os estudiosos coletaram o resultado de autópsias de pacientes que haviam morrido no hospital e, em seguida, os compararam aos diagnósticos feitos por seus médicos enquanto estavam vivos. A parte elegante dessa experiência é que os médicos também relataram a confiança que tinham nos próprios diagnósticos. Examinando apenas os casos em que os médicos tinham “certeza absoluta” dos diagnósticos, eles erraram com cerca de 40% dos pacientes.77 Errar sobre tantos diagnósticos é compreensível e talvez perdoável, já que os casos clínicos podem ser muito complicados, e também pelo que já vimos sobre a imperfeição dos exames. Mas ser tão autoconfiante é menos compreensível, porque significa que os médicos não estão prestando atenção aos resultados.

A sedução da medicina alternativa é que ela apela à genuína desconfiança que muitas pessoas sentem pela comunidade médica. Ela oferece a esperança, talvez romantizada, de que os produtos naturais ofereçam curas não invasivas, naturais. O uso da medicina alternativa muitas vezes alimenta uma crença naturalista de que se algo é baseado nas plantas, ou natural, deve ser bom. (Mas é claro que isso é falso: pense nos cogumelos venenosos, na trombeta, nas sementes de mamona, na cicuta.) Um problema adicional é que os medicamentos herbais e fitoterápicos não são regulamentados nos Estados Unidos e em muitos outros países. A U.S. Food and Drug Administration (FDA), órgão governamental responsável pelo controle de alimentos e medicamentos nos Estados Unidos, avalia que 70% das empresas não obedecem ao controle básico de qualidade.78 E embora o controle de qualidade seja um sério problema, com a presença de contaminadores e enchimentos numa grande quantidade de amostras, os próprios suplementos podem e causam danos, mesmo quando não são comprometidos pela baixa qualidade da manufatura. Um jovem de dezessete anos do Texas, Christopher Herrera, apareceu na emergência de um hospital em Houston, em 2012, com peito, rosto e olhos exibindo uma forte coloração amarela, “um amarelo quase como o de um marca-texto”, de acordo com o dr. Shreena Patel, o médico que o tratou.79 Ele sofrera danos no fígado depois de tomar uma xícara de um extrato de chá verde que havia comprado numa loja de produtos nutricionais, como suplemento para queima de gordura, e os danos foram de tal ordem que ele precisou fazer um transplante.80 Os suplementos dietéticos respondem hoje por 20% dos danos hepáticos relacionados aos remédios, triplicando a taxa de dez anos atrás.

No entanto, a maioria de nós conhece alguém que afirma ter sido curado por alguma forma de medicina alternativa, seja de uma gripe, uma dor lombar ou até um câncer. Um amigo querido recebeu um diagnóstico de câncer de próstata e ouviu dos médicos que tinha apenas seis meses de vida. “Dê um jeito em seus negócios e faça alguma coisa que sempre teve vontade de fazer”, disseram eles. “Férias no Havaí, quem sabe.” “O que eu sempre quis foi ter uma vida longa”, respondeu meu amigo, e foi embora.

Meu amigo ouviu falar de um médico especialista em medicina alternativa. O médico fez vários exames de sangue “alternativos” e, como resultado, receitou uma dieta e exercícios bem específicos. A lista de alimentos permitidos e proibidos era tão restritiva que ele levava de três a quatro horas só para preparar as refeições. Ele seguiu a dieta e o programa de exercícios com o mesmo empenho e a concentração que havia dedicado a cada aspecto de sua vida, o tipo de disciplina que o levara a ser presidente de uma renomada multinacional com apenas 38 anos de idade.

A sentença de morte de seis meses foi dada há doze anos. Meu amigo está em excelente forma, melhor do que nunca. Voltou a seus renomados oncologistas dois anos depois que estes lhe disseram que ele estaria morto, e eles lhe aplicaram uma bateria de exames. Seu PSA estava quase a zero, e todos os seus outros marcadores biológicos eram normais e estáveis. Eles se recusaram a acreditar que ele se curara apenas com uma dieta e exercícios. “Devia haver algo errado com os exames que fizemos na última vez que o vimos” foi a única coisa que conseguiram dizer.

Conheço meia dúzia de pessoas com as mesmas histórias. Elas são convincentes. Sou grato por meus amigos terem sobrevivido. O importante aqui é que não estamos falando de pesquisas científicas, apenas de casos — são inspiradores, misteriosos, desafiadores, mas apenas casos. O plural de história não é dados.81 Não houve controles experimentais, os pacientes não foram colocados aleatoriamente em uma condição ou em outra, não havia cientistas mantendo cuidadosos registros da progressão da doença ou da cura. Não tivemos a oportunidade de saber o que teria acontecido se meu amigo não tivesse mudado sua dieta e começado a praticar exercícios — ele poderia ter vivido tanto quanto viveu sem ter de passar oitenta horas por mês cortando verduras na cozinha. Ou poderia estar morto. Não faz muito tempo eu lhe perguntei se ele havia voltado para fazer uma biópsia ou ressonância magnética para ter certeza do desaparecimento do câncer. “Por que faria isso?”, perguntou ele. “Estou mais saudável do que nunca, me sinto ótimo, e não faria nada diferente do que fiz, se eles descobrissem algo.”

A derrota que meu amigo infligiu ao câncer através da dieta e do exercício não é consistente ou inconsistente com a ciência; está fora do escrutínio científico porque os dados não foram coletados de maneira científica.

Assim como os médicos ávidos em acreditar nas pontes de safena e angioplastias porque elas possuem um mecanismo plausível, estamos dispostos a acreditar, mesmo sem nenhum embasamento científico, que dieta e exercícios podem derrotar o câncer. É bastante plausível e intuitivamente compreensível. Nenhum de nós tem uma compreensão completa da relação entre dieta, exercício, doença e morte. Ouvimos o caso e pensamos “Sim, pode haver algo aí”. Para provar que baseamos esta crença na plausibilidade do mecanismo e não nos dados, imagine se em vez de dieta e exercício meu amigo dormisse de cabeça para baixo numa tenda em forma de pirâmide. Diríamos que ele é apenas maluco.

Uma das coisas boas da ciência é que ela está aberta a histórias como a do meu amigo, de modo a não perder a oportunidade de investigar novas e importantes curas. A maioria das descobertas científicas começa com uma simples observação, muitas vezes inesperada, e com a sorte, seguida de estudo cuidadoso; pense na maçã de Newton ou em Arquimedes deslocando a água na banheira.

Talvez, em estado latente, a cura do câncer ou de outras enfermidades esteja na “medicina alternativa”. Em centenas de laboratórios no mundo todo há pesquisas sendo feitas com preparações herbais, remédios e terapias alternativas. Mas, até que se mostrem eficazes, eles acarretam o perigo de levar os pacientes à demora em procurar tratamentos que já se mostraram funcionais, e assim de retardar a cura talvez até um ponto irreversível. Foi o que aconteceu com Steve Jobs — ele rejeitou a cirurgia para fazer um regime alternativo de acupuntura, suplementos dietéticos e sucos que veio a descobrir que não funcionava, retardando o tratamento convencional que, segundo os entendidos, poderia ter prolongado sua vida.82

Há milhares de pessoas nos Estados Unidos que morrem todo ano de doenças que poderiam ser prevenidas ou curadas pela “medicina ocidental”. O método científico promoveu um avanço maior da civilização nos últimos duzentos anos do que quaisquer outros métodos no decorrer dos 10 mil anos anteriores. Os pesquisadores médicos compreendem que nas suas experiências há vidas humanas em jogo — muitas vezes, mesmo antes de completado o teste clínico, os cientistas enxergam a existência de um claro benefício, e interrompem o teste mais cedo para logo liberar os medicamentos, em vez de fazer os pacientes esperarem, pois alguns estão tão doentes que esperar está fora de cogitação.

Na verdade, justamente porque terapias alternativas como a dieta e o exercício fazem tanto sentido, e porque existem tantas histórias como a do meu amigo, é que o Instituto Nacional de Saúde criou uma divisão de medicina complementar e alternativa para explorar tais tratamentos, usando todas as ferramentas da ciência moderna.83 Até agora, o instituto tem relatado muitos casos de nenhum ou pequeno efeito, chegando apenas a um reduzido número de pessoas que se beneficiam de terapias alternativas, e a um enorme número de outras que não se beneficiam.84 Em uma pesquisa típica, por exemplo, realizada num universo de 100 mil pessoas, uma parte recebeu aleatoriamente vitamina D, uma parte não recebeu nada, e a outra parte foi dado um placebo, de modo a testar a hipótese de a vitamina D ter um papel na prevenção do câncer e de doenças cardiovasculares.85 O resultado mostrou que é preciso que 150 pessoas sejam tratadas com vitamina D por cinco anos para que uma vida seja salva, mas as 149 que não tiveram benefício sofreram vários efeitos colaterais, inclusive pedras nos rins, fadiga, pancreatite e dor nos ossos. Não sabemos o efeito a longo prazo da terapia com vitamina D, e há nova evidência ligando o excesso de vitamina D à mortalidade.86 Mas ainda há muito trabalho a ser feito.

Como você pensa, o que você faz

Quando chega a hora de escolher qual a melhor opção de tratamento, você se encontra na maior parte das vezes sozinho. Terá de colher informações e aplicar a tabela quádrupla. Para alternativas que acarretam riscos semelhantes, a decisão pode ser difícil. Em parte, isso acontece porque as pessoas diferem muito quanto ao tamanho do risco que estão dispostas a aceitar, e ao tamanho do desconforto (tanto psicológico quanto físico) que estão dispostas a suportar. Esse lado do processo de tomada de decisão pelo paciente é muito bem descrito no livro de Jerome Groopman e Pamela Hartzband, Your Medical Mind [A mente médica dentro de nós].

Quais são seus preconceitos contra a medicina? Todos nós os temos. Groopman e Hartzband descrevem quatro tipos de pacientes:87 minimalista, maximalista, naturalista e tecnologista. O minimalista médico tenta interagir o menos possível com a medicina e os médicos. O maximalista acha que todo problema, dor ou desconforto tem uma solução médica. O naturalista acha que o corpo consegue se curar, talvez com a ajuda de medicamentos fitoterápicos ou espirituais. O tecnologista acredita que há sempre novas drogas e procedimentos melhores do que tudo que veio antes, e que são o melhor caminho a tomar.

Eles representam tipos extremos; a maioria de nós tem um pouco de cada um. Você pode ser um minimalista em relação à saúde dos dentes, mas um maximalista em relação ao botox e outros procedimentos “rejuvenescedores”. Você pode ser um naturalista quanto a gripes e resfriados, mas um tecnologista se precisar de uma cirurgia de apêndice. E essas orientações interagem. Há maximalistas naturalistas que têm prateleiras de remédios herbais, e minimalistas tecnologistas que fazem o mínimo possível, mas, se precisarem de uma cirurgia, exigirão a última palavra em cirurgia a laser guiada por robô. Compreender seus próprios preconceitos pode levar à tomada de decisões mais eficaz, e a um diálogo médico-paciente muito mais produtivo. Talvez seja especialmente útil contar logo a seu médico a qual desses estilos você tende.

Mas o valor de simplesmente compreender as probabilidades, o que dizem os números numa tabela quádrupla, sempre é útil e sempre será, a despeito de sua personalidade.

Você ouve dizer que se tomar certo remédio ou seguir certa dieta, isso reduzirá em 50% sua chance de pegar a doença X. Parece besteira. Mas guarde essas proporções básicas na cabeça. Pense na mulher de quarenta anos que estava pensando em ter filhos e foi informada de que, considerando sua idade (uma maneira bayesiana de enquadrar o problema), tinha cinco vezes mais chance de dar à luz um bebê com determinado defeito congênito. Imagine que a probabilidade de uma mulher mais jovem ter um filho com esse mesmo defeito fosse de apenas 1 em 50 mil, e que no caso da mulher de quarenta anos esse risco aumentasse para 1 em 10 mil. Ainda assim é uma ocorrência muito improvável. A incidência básica do defeito ainda é suficientemente baixa para que até mesmo um aumento de cinco vezes do risco, embora impressionante em termos percentuais, não tenha implicações práticas. Se isso lembra os embustes estatísticos no Capítulo 4 em relação às taxas mais baixas de divórcio para as pessoas que se conheceram na internet, você está absolutamente certo. Uma redução de 25% na taxa de divórcio, de 7,7% para 6%, não tem nenhuma importância no mundo de verdade. Um aumento ou uma diminuição de risco dessa ordem pode passar em testes de significância estatística (de importância principalmente para pesquisadores), mas ainda assim não fazer uma diferença significativa.

Por outro lado, se você está diante da probabilidade de 80% de um resultado catastrófico e pode reduzi-la em 25%, chegando a 60%, isso parece valer a pena — a redução de 25% é mais significativa na escala mais alta. Praticamente todos nós temos essa personalidade. Sabemos disso por causa de ideias elaboradas na psicologia e na economia comportamental, conhecidas como teoria da previsibilidade e utilidade esperada.88 Para a maioria de nós, tomadores de decisão humanos e não racionais, as perdas avultam mais do que os ganhos. Em outras palavras, a dor de perder cem dólares é maior do que o prazer de ganhar cem dólares. Colocando de outra maneira, a maioria de nós faria mais para evitar perder um ano de vida do que para ganhá-lo.

Uma das grandes intuições de Kahneman e Tversky foi que as perdas e os ganhos não são lineares, o que significa que o mesmo valor de ganho (ou perda) não causa a mesma satisfação (ou insatisfação) — eles são relativos ao seu estado atual. Se você está duro, ganhar um dólar é muito importante. Se for milionário, não é. Existem outras não linearidades: imagine que diagnosticaram determinada doença em você, e seu médico recomenda um tratamento que aumentará em 10% sua chance de recuperação. O aumento de 10% tem uma sensação diferente dependendo da sua chance inicial de recuperação. Imagine os seguintes cenários:

1. Aumentar sua chance de recuperação de 0% para 10%.
2. Aumentar sua chance de recuperação de 10% para 20%.
3. Aumentar sua chance de recuperação de 45% para 55%.
4. Aumentar sua chance de recuperação de 90% para 100%.

Se você for como a maioria das pessoas, os cenários A e D parecem mais atraentes do que B e C. O cenário A transforma a certeza da morte em possibilidade de vida. É uma possibilidade pequena, mas somos programados para nos agarrar à vida e olhar para o lado mais favorável quando obrigados a enfrentar alternativas assim. O cenário D muda a possibilidade de morte para a certeza de vida.89 Agarramos as chances A ou D; queremos mais informação sobre B e C para decidir se valem a pena.

Nosso sistema intuitivo não é bem configurado para compreender as estatísticas ou tomar decisões racionais em cada caso — essa é a principal questão por trás de Rápido e devagar: duas formas de pensar, de Daniel Kahneman.90 Como exemplo, a maioria de nós é tão sensível à maneira como um problema é apresentado — à forma como é enquadrado — que manipulações simples e até ridículas podem influir dramaticamente em escolhas e preferências.91 Por exemplo, considere os dados hipotéticos sobre os resultados da cirurgia de câncer contrapostos aos da radiação. Qual você escolheria?

1a De cem pessoas que se submetem à cirurgia, noventa sobrevivem ao procedimento, e 34 ainda estão vivas cinco anos depois.

1b De cem pessoas submetidas à radioterapia, todas sobrevivem ao tratamento, e 22 ainda estão vivas cinco anos depois.

Se você escolhe a cirurgia, é como a maioria das pessoas — o resultado após cinco anos parece mais atraente, mesmo quando contraposto ao fato de que o resultado imediato é melhor com a radiação.

Agora que os dados são reformulados em termos de mortalidade, em vez de sobrevivência, qual você preferiria?

2a De cem pessoas submetidas à cirurgia, dez morrem durante o procedimento, e 66 morrem até cinco anos depois.

2b De cem pessoas submetidas à radioterapia, nenhuma morre durante o tratamento, e 78 morrem até cinco anos depois.92

Essas duas formulações do problema, ou enquadramentos, são claramente idênticas do ponto de vista matemático — dez de cem morrendo é o mesmo que noventa de cem vivendo —, mas não são psicologicamente idênticas. As pessoas tendem mais a escolher a cirurgia no primeiro caso, e a radiação, no segundo. Na primeira dupla de cenários, nossa atenção é aparentemente atraída pela diferença nos resultados cinco anos depois, quando 34% dos pacientes submetidos à cirurgia estão vivos, contra 22% dos que se submeteram à radiação. O enquadramento da segunda dupla de cenários aparentemente chama nossa atenção para o risco do próprio procedimento: a radiação reduz o risco da morte imediata de 10% para 0%. O efeito de enquadramento foi notado não apenas nos pacientes, mas em médicos experientes e executivos estatisticamente sofisticados.

Outro aspecto do enquadramento é que a maioria de nós é melhor com figuras do que com puros números, uma das motivações para introduzir no currículo de cálculo nas universidades apresentações de base gráfica para o material difícil.93 Uma das maneiras que médicos tentaram para ajudar os pacientes a compreender melhor os riscos foi mostrar visualmente os vários resultados para um grupo de cem pacientes. Aqui, neste exemplo, estão os riscos e benefícios do tratamento com antibióticos para otite média. O número de pessoas a tratar é vinte (de cem pessoas que receberam antibióticos, cinco serão beneficiadas). Além disso, nove pessoas não serão curadas e precisarão de acompanhamento posterior. Do grupo, 86 não são auxiliadas nem prejudicadas — ao menos não fisicamente (talvez financeiramente). Trata-se de muito antibiótico sendo tomado com um benefício muito pequeno. Mas gráficos como o que apresento a seguir podem ajudar esses pacientes a compreender o risco e a tomar decisões melhores, porque eles conseguem ver a proporção de pessoas em cada categoria.94

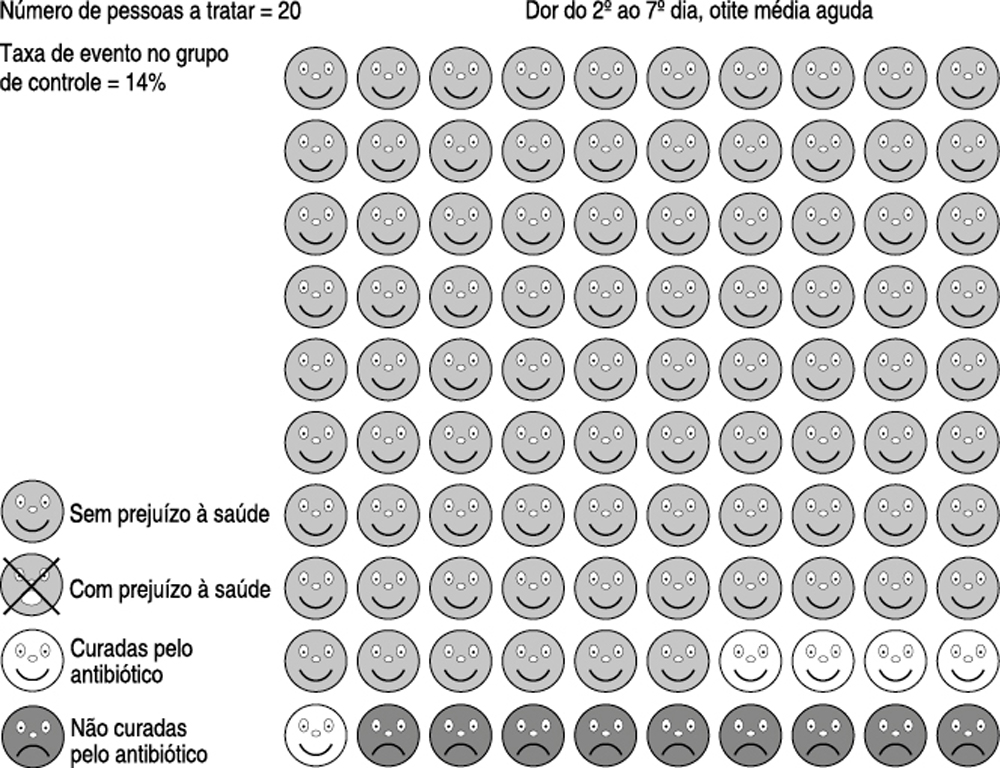
Outro aspecto da psicologia da tomada de decisão de todo mundo é o arrependimento. Amos Tversky ensinou que a aversão ao risco é motivada pelo arrependimento, uma poderosa força psicológica. Tendemos a tomar decisões para evitar o arrependimento que pode surgir por termos tomado decisões erradas, mesmo que as escolhas fossem marcadamente contrastantes em termos do valor esperado. Embora o tratamento X tenha apenas a chance de 10% de ser útil e um alto risco de efeitos colaterais, talvez você o escolha para não ter de viver com o arrependimento de saber mais tarde que você era um dos 10% que se beneficiariam dele. O custo emocional do arrependimento pode ser enorme. Como disse uma sobrevivente de câncer de mama, “eles me disseram que não sabiam se a quimioterapia depois da cirurgia seria útil ou não. Mas eu não parava de pensar: e se o câncer de mama voltar e eu não tiver feito o tratamento? Eu me sentiria uma idiota”.

Os dois pneus dianteiros do meu carro têm cinco anos, e os sulcos ainda estão bastante bons no centro, mas notei algum desgaste nas beiradas (isso pode acontecer por calibragem baixa ou por andar muito em terreno montanhoso). Consultei um borracheiro e ele frisou que, após cinco anos, a borracha dos pneus se torna quebradiça e pode rachar, fazendo com que os frisos e feixes se separem da carcaça.95 Isso, somado ao desgaste dos sulcos nas bordas, deixa os pneus muito vulneráveis e eles podem estourar.

Bem, sou motorista há muitos anos, já dirigi por centenas de milhares de quilômetros, e só fui vítima de estouro de pneu duas ou três vezes na vida. Não foram situações de perigo, mas deram trabalho. Você precisa encostar, pegar o macaco, suspender o carro e pôr o pneu sobressalente. Se tudo der certo, você simplesmente chega meia hora atrasado ao compromisso, com as roupas meio sujas. Por outro lado, se isso acontecer durante uma tempestade, ou numa estrada montanhosa, ou numa rodovia sem acostamento, pode ser uma situação muito mais desagradável e talvez perigosa. Nem o meu mecânico nem o Departamento de Trânsito podem estimar se meus pneus vão estourar antes que os sulcos centrais se desgastem tanto a ponto de precisarem ser trocados. Mesmo não tendo essa informação, meu palpite — e o palpite do meu mecânico — é que o valor ou benefício esperado de substituir os dois pneus é muito menor do que o custo de substituí-los.

Meu amigo Allan adora poupar dinheiro. Quero dizer, ele adora fazer economia, e sempre nos conta de pratos que comprou em lojas de artigos baratos e de roupas que adquiriu no brechó do Exército de Salvação. Não que ele não possa gastar mais — ele tem bastante dinheiro —, apenas se sente um campeão em desafiar a cultura do consumo do mundo moderno. Allan teria grande orgulho de poder se vangloriar de ter poupado duzentos dólares conservando seus velhos pneus, e está disposto a correr o risco de alguma probabilidade desconhecida ou incômodo no futuro. Quanto a mim, prefiro trocar dinheiro por conforto e segurança. Outras pessoas gostam dessa segurança adicional e estão dispostas a pagar por ela. O seguro, no fundo, é isso — se o seguro contra incêndio fosse um negócio tão bom para os proprietários de casas, as companhias de seguro não seriam as ricas multinacionais que são; não tenham dúvida, é um bom negócio para elas. Mas gostamos da paz de espírito que o seguro garante. Eu comprei pneus novos. (Allan leu este trecho e gostaria que eu lhe dissesse que acha que tomei essa decisão movido por temores irracionais, e que vivo me ­preocupando por qualquer coisa.)

O arrependimento desempenha um enorme papel em decisões como essa. Se eu estragar um belo piquenique, ou um belo conjunto de roupas, ou acabar sofrendo um desastre porque não gastei aqueles duzentos dólares, vou me sentir um idiota. Se Allan conseguir usar os pneus gastos por mais dois anos, vai brandir os duzentos dólares na minha cara, todo contente, e me dizer como fui tolo por ser tão preocupado.

É evidente que a tomada de decisão médica também é movida pelo medo do arrependimento. Alguns estão dispostos a enfrentar aborrecimento e desconforto agora para evitar até a pequena chance de 5% de algo dar errado e de um arrependimento como: “Se eu ao menos tivesse seguido a recomendação do médico! O que foi que me deu? A minha vida estava em jogo!”. Allan, por outro lado, quer maximizar seus prazeres momentâneos, e dá valor à liberdade de fazer o que quer, livre de regimes de saúde ou procedimentos médicos que não sejam absolutamente necessários hoje.

A melhor estratégia para organizar a informação médica em casos assim é se armar das estatísticas mais precisas que se possa obter, além de compreender seus próprios preconceitos e sua disposição de correr riscos e suportar o arrependimento. Se você se sentir perdido e confuso, amigos e familiares muitas vezes podem ajudá-lo a lembrar os valores fundamentais que norteiam a sua vida.

Medicina, matemática e a tomada de decisões significativas

Os demais capítulos deste livro se preocuparam especialmente com a atenção e a memória, mas o grande trunfo para tomar decisões sobre coisas importantes é a matemática, a chamada rainha das ciências. Às vezes pode parecer que se trata de aritmética chata e insossa, mas, para organizarmos nosso raciocínio sobre a vida, acabaremos tendo de abrir mão, em última instância, da nossa eterna antipatia pela aparente desumanidade da análise probabilística e dos cálculos matemáticos.

Nesses momentos, quando você enfrenta uma decisão difícil com as mais sérias consequências, quando está com medo, perplexo e frustrado, quando a vida está de fato em jogo, deposite sua fé nos números. Tente colher o máximo de informação possível e processe-a junto a quem entende do assunto. Se precisar fazer uma cirurgia, escolha um médico que já realizou muitos procedimentos. Como CEO de seu próprio plano de saúde, você precisa compreender como pegar a informação dada pelos médicos para analisá-la em tabelas quádruplas, aplicando o raciocínio bayesiano, porque isso acabará com muita adivinhação na tomada de decisão médica, transformando-a em números que você poderá facilmente avaliar, já que a maioria de nós não possui a intuição refinada de um dr. Gregory House.

Leve algum tempo para tomar a decisão, e pense nela de uma perspectiva matemática. Converse com seu médico, e, se seu médico não se sentir à vontade discutindo estatística, procure outro. É importante superar sua relutância em fazer perguntas ou discutir com o médico. Leve algum ente querido para apoiá-lo. Assegure-se de que a consulta dure bastante — pergunte ao médico: “Quanto tempo poderá me conceder?”.

Quando estamos doentes ou machucados, nossa vida parece controlada por especialistas, mas não precisa ser assim. Podemos assumir o controle de nossas próprias doenças, aprender o máximo possível sobre elas, e pedir conselho a mais de um médico. Os médicos também são pessoas, é claro, e demonstram muitos tipos de personalidade, estilo e pontos fortes. Vale a pena encontrar alguém cujo estilo combine com o seu, alguém que compreenda suas necessidades e possa ajudá-lo a enfrentá-las. Sua relação com o médico não deve ser de filho com pai, mas de parceiros capazes de atuar juntos na tarefa de atingir uma meta comum.