II.3 The Development of Abstract Algebra
Karen Hunger Parshall
1 Introduction
What is algebra? To the high school student encountering it for the first time, algebra is an unfamiliar abstract language of x’s and y’s, a’s and b’s, together with rules for manipulating them. These letters, some of them variables and some constants, can be used for many purposes. For example, one can use them to express straight lines as equations of the form y = ax + b, which can be graphed and thereby visualized in the Cartesian plane. Furthermore, by manipulating and interpreting these equations, it is possible to determine such things as what a given line’s root is (if it has one)—that is, where it crosses the x-axis—and what its slope is—that is, how steep or flat it appears in the plane relative to the axis system. There are also techniques for solving simultaneous equations, or equivalently for determining when and where two lines intersect (or demonstrating that they are parallel).
Just when there already seem to be a lot of techniques and abstract manipulations involved in dealing with lines, the ante is upped. More complicated curves like quadratics, y = ax2 + bx + c, and even cubics, y = ax3 + bx2 + cx + d, and quartics, y = ax4 + bx3 + cx2 + dx + e, enter the picture, but the same sort of notation and rules apply, and similar sorts of questions are asked. Where are the roots of a given curve? Given two curves, where do they intersect?
Suppose now that the same high school student, having mastered this sort of algebra, goes on to university and attends an algebra course there. Essentially gone are the by now familiar x’s, y’s, a’s, and b’s; essentially gone are the nice graphs that provide a way to picture what is going on. The university course reflects some brave new world in which the algebra has somehow become “modern.” This modern algebra involves abstract structures—GROUPS [I.3 §2.1], RINGS [III.81 §1], FIELDS [I.3 §2.2], and other so-called objects—each one defined in terms of a relatively small number of axioms and built up of substructures like subgroups, ideals, and subfields. There is a lot of moving around between these objects, too, via maps like group homomorphisms and ring AUTOMORPHISMS [I.3 §4.1]. One objective of this new type of algebra is to understand the underlying structure of the objects and, in doing so, to build entire theories of groups or rings or fields. These abstract theories may then be applied in diverse settings where the basic axioms are satisfied but where it may not be at all apparent a priori that a group or a ring or a field may be lurking. This, in fact, is one of modern algebra’s great strengths: once we have proved a general fact about an algebraic structure, there is no need to prove that fact separately each time we come across an instance of that structure. This abstract approach allows us to recognize that contexts that may look quite different are in fact importantly similar.
How is it that two endeavors—the high school analysis of polynomial equations and the modern algebra of the research mathematician—so seemingly different in their objectives, in their tools, and in their philosophical outlooks are both called “algebra”? Are they even related? In fact, they are, but the story of how they are is long and complicated.
2 Algebra before There Was Algebra: From Old Babylon to the Hellenistic Era
Solutions of what would today be recognized as first-and second-degree polynomial equations may be found in Old Babylonian cuneiform texts that date to the second millennium B.C.E. However, these problems were neither written in a notation that would be recognizable to our modern-day high school student nor solved using the kinds of general techniques so characteristic of the high school algebra classroom. Rather, particular problems were posed, and particular solutions obtained, from a series of recipe-like steps. No general theoretical justification was given, and the problems were largely cast geometrically, in terms of measurable line segments and surfaces of particular areas. Consider, for example, this problem, translated and transcribed from a clay tablet held in the British Museum (catalogued as BM 13901, problem 1) that dates from between 1800 and 1600 B.C.E.:
This may be translated into modern notation as the equation x2 + 1x = 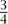 , where it is important to notice that the Babylonian number system is base 60, so 45' denotes
, where it is important to notice that the Babylonian number system is base 60, so 45' denotes 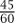 =
= 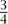 . The text then lays out the following algorithm for solving the problem: take 1, the coefficient of the linear term, and halve it to get
. The text then lays out the following algorithm for solving the problem: take 1, the coefficient of the linear term, and halve it to get  . Square
. Square  to get
to get 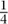 . Add
. Add 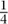 to
to 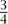 , the constant term, to get 1. This is the square of 1. Subtract from this the
, the constant term, to get 1. This is the square of 1. Subtract from this the  which you multiplied by to get
which you multiplied by to get  , the side of the square. The modern reader can easily see that this algorithm is equivalent to what is now called the quadratic formula, but the Babylonian tablet presents it in the context of a particular problem and repeats it in the contexts of other particular problems. There are no equations in the modern sense; the Babylonian writer is literally effecting a construction of plane figures. Similar problems and similar algorithmic solutions can also be found in ancient Egyptian texts such as the Rhind papyrus, believed to have been copied in 1650 B.C.E. from a text that was about a century and a half older.
, the side of the square. The modern reader can easily see that this algorithm is equivalent to what is now called the quadratic formula, but the Babylonian tablet presents it in the context of a particular problem and repeats it in the contexts of other particular problems. There are no equations in the modern sense; the Babylonian writer is literally effecting a construction of plane figures. Similar problems and similar algorithmic solutions can also be found in ancient Egyptian texts such as the Rhind papyrus, believed to have been copied in 1650 B.C.E. from a text that was about a century and a half older.
There is a sharp contrast between the problem-oriented, untheoretical approach characteristic of texts from this early period and the axiomatic and deductive approach that EUCLID [VI.2] introduced into mathematics in around 300 B.C.E. in his magisterial, geometrical treatise, the Elements. (See GEOMETRY [II.2] for a further discussion of this work.) There, building on explicit definitions and a small number of axioms or self-evident truths, Euclid proceeded to deduce known—and almost certainly some hitherto unknown—results within a strictly geometrical context. Geometry done in this axiomatic context defined Euclid’s standard of rigor. But what does this quintessentially geometrical text have to do with algebra? Consider the sixth proposition in Euclid’s Book II, ostensibly a book on plane figures, and in particular quadrilaterals:
While clearly a geometrical construction, it equally clearly describes two constructions—one a rectangle and one a square—that have equal areas. It therefore describes something that we should be able to write as an equation. Figure 1 gives the picture corresponding to Euclid’s construction: he proves that the area of rectangle ADMK equals the sum of rectangles CDML and HMFG. To do this, he adds the square on CB—namely, square LHGE—to CDML and HMFG. This gives square CDFE. It is not hard to see that this is equivalent to the high school procedure of “completing the square” and to the algebraic equation (2a + b)b + a2 = (a + b)2, which we obtain by setting CB = a and BD = b. Equivalent, yes, but for Euclid this is a specific geometrical construction and a particular geometrical equivalence. For this reason, he could not deal with anything but positive real quantities, since the sides of a geometrical figure could only be measured in those terms. Negative quantities did not and could not enter into Euclid’s fundamentally geometrical mathematical world. Nevertheless, in the historical literature, Euclid’s Book II has often been described as dealing with “geometrical algebra,” and, because of our easy translation of the book’s propositions into the language of algebra, it has been argued, albeit ahistorically, that Euclid had algebra but simply presented it geometrically.
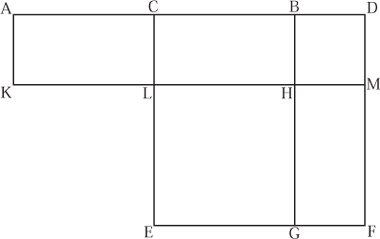
Figure 1 The sixth proposition from Euclid’s Book II.
Although Euclid’s geometrical standard of rigor came to be regarded as a pinnacle of mathematical achievement, it was in many ways not typical of the mathematics of classical Greek antiquity, a mathematics that focused less on systematization and more on the clever and individualistic solution of particular problems. There is perhaps no better exemplar of this than ARCHIMEDES [VI.3], held by many to have been one of the three or four greatest mathematicians of all time. Still, Archimedes, like Euclid, posed and solved particular problems geometrically. As long as geometry defined the standard of rigor, not only negative numbers but also what we would recognize as polynomial equations of degree higher than three effectively fell outside the sphere of possible mathematical discussion. (As in the example from Euclid above, quadratic polynomials result from the geometrical process of completing the square; cubics could conceivably result from the geometrical process of completing the cube; but quartics and higher-degree polynomials could not be constructed in this way in familiar, three-dimensional space.) However, there was another mathematician of great importance to the present story, Diophantus of Alexandria (who was active in the middle of the third century C.E.). Like Archimedes, he posed particular problems, but he solved them in an algorithmic style much more reminiscent of the Old Babylonian texts than of Archimedes’ geometrical constructions, and as a result he was able to begin to exceed the bounds of geometry.
In his text Arithmetica, Diophantus put forward general, indeterminate problems, which he then restricted by specifying that the solutions should have particular forms, before providing specific solutions. He expressed these problems in a very different way from the purely rhetorical style that held sway for centuries after him. His notation was more algebraic and was ultimately to prove suggestive to sixteenth-century mathematicians (see below). In particular, he used special abbreviations that allowed him to deal with the first six positive and negative powers of the unknown as well as with the unknown to the zeroth power. Thus, whatever his mathematics was, it was not the “geometrical algebra” of Euclid and Archimedes.
Consider, for example, this problem from Book II of the Arithmetica: “To find three numbers such that the square of any one of them minus the next following gives a square.” In terms of modern notation, he began by restricting his attention to solutions of the form (x + 1, 2x + 1, 4x + 1). It is easy to see that (x+1)2 - (2x+1) = x2 and (2x+1)2-(4x+1) = 4x2, so two of the conditions of the problem are immediately satisfied, but he needed (4x+1)2-(x+1) = 16x2 + 7x to be a square as well. Arbitrarily setting 16x2 + 7x 25x2, Diophantus then determined that x = 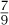 gave him what he needed, so a solution was
gave him what he needed, so a solution was 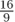 ,
, 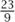 ,
, 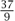 , and he was done. He provided no geometrical justification because in his view none was needed; a single numerical solution was all he required. He did not set up what we would recognize as a more general set of equations and try to find all possible solutions.
, and he was done. He provided no geometrical justification because in his view none was needed; a single numerical solution was all he required. He did not set up what we would recognize as a more general set of equations and try to find all possible solutions.
Diophantus, who lived more than four centuries after Archimedes’ death, was doing neither geometry nor algebra in our modern sense, yet the kinds of problems and the sorts of solutions he obtained for them were very different from those found in the works of either Euclid or Archimedes. The extent to which Diophantus created a wholly new approach, rather than drawing on an Alexandrian tradition of what might be called “algorithmic algebraic,” as opposed to “geometric algebraic,” scholarship is unknown. It is clear that by the time Diophantus’s ideas were introduced into the Latin West in the sixteenth century, they suggested new possibilities to mathematicians long conditioned to the authority of geometry.
3 Algebra before There Was Algebra: The Medieval Islamic World
The transmission of mathematical ideas was, however, a complex process. After the fall of the Roman Empire and the subsequent decline of learning in the West, both the Euclidean and the Diophantine traditions ultimately made their way into the medieval Islamic world. There they were not only preserved—thanks to the active translation initiatives of Islamic scholars—but also studied and extended.
AL-KHW RIZM
RIZM [VI.5] was a scholar at the royally funded House of Wisdom in Baghdad. He linked the kinds of geometrical arguments Euclid had presented in Book II of his Elements with the indigenous problemsolving algorithms that dated back to Old Babylonian times. In particular, he wrote a book on practical mathematics, entitled al-Kit
[VI.5] was a scholar at the royally funded House of Wisdom in Baghdad. He linked the kinds of geometrical arguments Euclid had presented in Book II of his Elements with the indigenous problemsolving algorithms that dated back to Old Babylonian times. In particular, he wrote a book on practical mathematics, entitled al-Kit b al-mukhtasar f
b al-mukhtasar f his
his b al-jabr wa’1-muq
b al-jabr wa’1-muq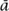 bala (“The compendious book on calculation by completion and balancing”), beginning it with a theoretical discussion of what we would now recognize as polynomial equations of the first and second degrees. (The latinization of the word “al-jabr” or “completion” in his title gave us our modern term “algebra.”) Because he employed neither negative numbers nor zero coefficients, al-Khwārizmī provided a systematization in terms of six separate kinds of examples where we would need just one, namely ax2 + bx + c = 0. He considered, for example, the case when “a square and 10 roots are equal to 39 units,” and his algorithmic solution in terms of multiplications, additions, and subtractions was in precisely the same form as the above solution from tablet BM 13901. This, however, was not enough for al-Khwārizmī. “It is necessary,” he said, “that we should demonstrate geometrically the truth of the same problems which we have explained in numbers,” and he proceeded to do this by “completing the square” in geometrical terms reminiscent of, but not as formal as, those Euclid used in Book II. (Ab
bala (“The compendious book on calculation by completion and balancing”), beginning it with a theoretical discussion of what we would now recognize as polynomial equations of the first and second degrees. (The latinization of the word “al-jabr” or “completion” in his title gave us our modern term “algebra.”) Because he employed neither negative numbers nor zero coefficients, al-Khwārizmī provided a systematization in terms of six separate kinds of examples where we would need just one, namely ax2 + bx + c = 0. He considered, for example, the case when “a square and 10 roots are equal to 39 units,” and his algorithmic solution in terms of multiplications, additions, and subtractions was in precisely the same form as the above solution from tablet BM 13901. This, however, was not enough for al-Khwārizmī. “It is necessary,” he said, “that we should demonstrate geometrically the truth of the same problems which we have explained in numbers,” and he proceeded to do this by “completing the square” in geometrical terms reminiscent of, but not as formal as, those Euclid used in Book II. (Ab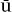 K
K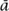 mil (ca. 850-930), an Egyptian Islamic mathematician of the generation after al-Khwārizmī, introduced a higher level of Euclidean formality into the geometric-algorithmic setting.) This juxtaposition made explicit how the relationships between geometrical areas and lines could be interpreted in terms of numerical multiplications, additions, and subtractions, a key step that would ultimately suggest a move away from the geometrical solution of particular problems and toward an algebraic solution of general types of equations.
mil (ca. 850-930), an Egyptian Islamic mathematician of the generation after al-Khwārizmī, introduced a higher level of Euclidean formality into the geometric-algorithmic setting.) This juxtaposition made explicit how the relationships between geometrical areas and lines could be interpreted in terms of numerical multiplications, additions, and subtractions, a key step that would ultimately suggest a move away from the geometrical solution of particular problems and toward an algebraic solution of general types of equations.
Another step along this path was taken by the mathematician and poet Omar Khayyam (ca. 1050–1130) in a book he entitled Al-jabr after al-Khwārizmī’s work. Here he proceeded to systematize and solve what we would recognize, in the absence of both negative numbers and zero coefficients, as the cases of the cubic equation. Following al-Khwārizmī, Khayyam provided geometrical justifications, yet his work, even more than that of his predecessor, may be seen as closer to a general problem-solving technique for specific cases of equations, that is, closer to the notion of algebra.
The Persian mathematician al-Karaj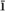 (who flourished in the early eleventh century) also knew well and appreciated the geometrical tradition stemming from Euclid’s Elements. However, like Ab
(who flourished in the early eleventh century) also knew well and appreciated the geometrical tradition stemming from Euclid’s Elements. However, like Ab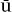 -Kamil, he was aware of the Diophantine tradition too, and synthesized in more general terms some of the procedures Diophantus had laid out in the context of specific examples in the Arithmetica. Although Diophantus’s ideas and style were known to these and other medieval Islamic mathematicians, they would remain unknown in the Latin West until their rediscovery and translation in the sixteenth century. Equally unknown in the Latin West were the accomplishments of Indian mathematicians, who had succeeded in solving some quadratic equations algorithmically by the beginning of the eighth century and who, like Bragmagupta four hundred years later, had techniques for finding integer solutions to particular examples of what are today called Pell’s equations, namely, equations of the form ax2 + b = y2, where a and b are integers and a is not a square.
-Kamil, he was aware of the Diophantine tradition too, and synthesized in more general terms some of the procedures Diophantus had laid out in the context of specific examples in the Arithmetica. Although Diophantus’s ideas and style were known to these and other medieval Islamic mathematicians, they would remain unknown in the Latin West until their rediscovery and translation in the sixteenth century. Equally unknown in the Latin West were the accomplishments of Indian mathematicians, who had succeeded in solving some quadratic equations algorithmically by the beginning of the eighth century and who, like Bragmagupta four hundred years later, had techniques for finding integer solutions to particular examples of what are today called Pell’s equations, namely, equations of the form ax2 + b = y2, where a and b are integers and a is not a square.
4 Algebra before There Was Algebra: The Latin West
Concurrent with the rise of Islam in the East, the Latin West underwent a gradual cultural and political stabilization in the centuries following the fall of the Roman Empire. By the thirteenth century, this relative stability had resulted in the firm entrenchment of the Catholic Church as well as the establishment both of universities and of an active economy. Moreover, the Islamic conquest of most of the Iberian peninsula in the eighth century and the subsequent establishment there of an Islamic court, library, and research facility similar to the House of Wisdom in Baghdad brought the fruits of medieval Islamic scholarship to western Europe’s doorstep. However, as Islam found its position on the Iberian peninsula increasingly compromised in the twelfth and thirteenth centuries, this Islamic learning, as well as some of the ancient Greek scholarship that the medieval Islamic scholars had preserved in Latin translation, began to filter into medieval Europe. In particular, FIBONACCI [VI.6], son of an influential administrator within the Pisan city state, encountered al-Khwārizmī’s text and recognized not only the impact that the Arabic number system detailed there could have on accounting and commerce (Roman numerals and their cumbersome rules for manipulation were still widely in use) but also the importance of al-Khwārizmī’s theoretical discussion, with its wedding of geometrical proof and the algorithmic solution of what we can interpret as first- and second-degree equations. In his 1202 book Liber Abbaci, Fibonacci presented al-Khwārizmī’s work almost verbatim, and extolled all of these virtues, thus effectively introducing this knowledge and approach into the Latin West.
Fibonacci’s presentation, especially of the practical aspects of al-Khwārizmī’s text, soon became well-known in Europe. So-called abacus schools (named after Fibonacci’s text and not after the Chinese calculating instrument) sprang up all over the Italian peninsula, particularly in the fourteenth and fifteenth centuries, for the training of accountants and bookkeepers in an increasingly mercantilistic Western world. The teachers in these schools, the “maestri d’abaco,” built on and extended the algorithms they found in Fibonacci’s text. Another tradition, the Cossist tradition—after the German word “Coss” connoting algebra, that is, “Kunstrechnung” or “artful calculation”—developed simultaneously in the Germanic regions of Europe and aimed to introduce algebra into the mainstream there.
In 1494 the Italian Luca Pacioli published (by now this is the operative word: Pacioli’s text is one of the earliest printed mathematical texts) a compendium of all known mathematics. By this time, the geometrical justifications that al-Khwārizmī and Fibonacci had presented had long since fallen from the mathematical vernacular. By reintroducing them in his book, the Summa, Pacioli brought them back to the mathematical fore. Not knowing of Khayyam’s work, he asserted that solutions had been discovered only in the six cases treated by both al-Khwārizmī and Fibonacci, even though there had been abortive attempts to solve the cubic and even though he held out the hope that it could ultimately be solved.
Pacioli’s book had highlighted a key unsolved problem: could algorithmic solutions be determined for the various cases of the cubic? And, if so, could these be justified geometrically with proofs similar in spirit to those found in the texts of al-Khwārizmī and Fibonacci?
Among several sixteenth-century Italian mathematicians who eventually managed to answer the first question in the affirmative was CARDANO [VI.7]. In his Ars Magna, or The Great Art, of 1545, he presented algorithms with geometric justifications for the various cases of the cubic, effectively completing the cube where al-Khwārizmī and Fíbonaccí had completed the square. He also presented algorithms that had been discovered by his student Ludovico Ferrari (1522–65) for solving the cases of the quartic. These intrigued him, because, unlike the algorithms for the cubic, they were not justified geometrically. As he put it in his book, “all those matters up to and including the cubic are fully demonstrated, but the others which we will add, either by necessity or out of curiosity, we do not go beyond barely setting out.” An algebra was breaking out of the geometrical shell in which it had been encased.
5 Algebra Is Born
This process was accelerated by the rediscovery and translation into Latin of Diophantus’s Arithmetica in the 1560s, with its abbreviated presentational style and ungeometrical approach. Algebra, as a general problem-solving technique, applicable to questions in geometry, number theory, and other mathematical settings, was established in RAPHAEL BOMBELLI’S [VI.8] Algebra of 1572 and, more importantly, in VIÉTE’S [VI.9] In Artem Analyticem Isagoge, or Introduction to the Analytic Art, of 1591. The aim of the latter was, in Viète’s “words, “to leave no problem unsolved,” and to this end he developed a true notation—using vowels to denote variables and consonants to denote coefficients—as well as methods for solving equations in one unknown. He called his techniques “specious logistics.”
Dimensionality—in the form of his so-called law of homogeneity—was, however, still an issue for Viète. As he put it, “[o]nly homogeneous magnitudes are to be compared to one another.” The problem was that he distinguished two types of magnitudes: “ladder magnitudes”—that is, variables (A side) (or x in our modern notation), (A square) (or x2), (A cube) (or x3), etc.; and “compared magnitudes”—that is, coefficients (B length) of dimension one, (B plane) of dimension two, (B solid) of dimension three, etc. In the light of his law of homogeneity, then, Viète could legitimately perform the operation (A cube) + (B plane)(A side) (or x3+ bx in our notation), since the dimension of (A cube) is three, as is that of the product of the two-dimensional coefficient (B plane) and the one-dimensional variable (A side), but he could not legally add the three-dimensional variable (A cube) to the two-dimensional product of the one-dimensional coefficient (B length) and the one-dimensional variable (A side) (or, again, x3 + bx in our notation). Be this as it may, his “analytic art” still allowed him to add, subtract, multiply, and divide letters as opposed to specific numbers, and those letters, as long as they satisfied the law of homogeneity, could be raised to the second, third, fourth, or, indeed, any power. He had a rudimentary algebra, although he failed to apply it to curves.
The first mathematicians to do that were FERMAT [VI.12] and DESCARTES [VI.11] in their independent development of the analytic geometry so familiar to the high school algebra student of today. Fermat, and others like Thomas Harriot (ca. 1560–1621) in England, were influenced in their approaches by Viète, while Descartes not only introduced our present-day notational convention of representing variables by x’s and y’s and constants by a’s, b’s, and c’s but also began the arithmetization of algebra. He introduced a unit that allowed him to interpret all geometrical magnitudes as line segments, whether they were x’s, x2’s, x3’s, x4’s, or any higher power of x, thereby removing concerns about homogeneity. Fermat’s main work in this direction was a 1636 manuscript written in Latin, entitled “Introduction to plane and solid loci” and circulated among the early seventeenth-century mathematical cognoscenti; Descartes’s was La Géométrie, written in French as one of three appendices to his philosophical tract, Discours de la Méthode, published in 1637. Both were regarded as establishing the identification of geometrical curves with equations in two unknowns, or in other words as establishing analytic geometry and thereby introducing algebraic techniques into the solution of what had previously been considered geometrical problems. In Fermat’s case, the curves were lines or conic sections—quadratic expressions in x and y; Descartes did this too, but he also considered equations more generally, tackling questions about the roots of polynomial equations that were connected with transforming and reducing the polynomials.
In particular, although he gave no proof or even general statement of it, Descartes had a rudimentary version of what we would now call THE FUNDAMENTAL THEOREM OF ALGEBRA [V.13], the result that a polynomial equation xn + an-1xn-1 + · · · + a1x + a0 of degree n has precisely n roots over the field ℂ of complex numbers. For example, while he held that a given polynomial of degree n could be decomposed into n linear factors, he also recognized that the cubic x3 - 6x2 + 13x - 10 = 0 has three roots: the real root 2 and two complex roots. In his further exploration of these issues, moreover, he developed algebraic techniques, involving suitable transformations, for analyzing polynomial equations of the fifth and sixth degrees. Liberated from homogeneity concerns, Descartes was thus able to use his algebraic techniques freely to explore territory where the geometrically bound Cardano had clearly been reluctant to venture. NEWTON [VI.14] took the liberation of algebra from geometrical concerns a step further in his Arithmetica Universalis (or Universal Arithmetic) of 1707, arguing for the complete arithmetization of algebra, that is, for modeling algebra and algebraic operations on the real numbers and the usual operations of arithmetic.
Descartes’s La Géométrie highlighted at least two problems for further algebraic exploration: the fundamental theorem of algebra and the solution of polynomial equations of degree greater than four. Although eighteenth-century mathematicians like D’ALEMBERT [VI.20] and EULER [VI.19] attempted proofs of the fundamental theorem of algebra, the first person to prove it rigorously was GAUSS [VI.26], who gave four distinct proofs over the course of his career. His first, an algebraic geometrical proof, appeared in his doctoral dissertation of 1799, while a second, fundamentally different proof was published in 1816, which in modern terminology essentially involved constructing the polynomial’s splitting field. While the fundamental theorem of algebra established how many roots a given polynomial equation has, it did not provide insight into exactly what those roots were or how precisely to find them. That problem and its many mathematical repercussions exercised a number of mathematicians in the late eighteenth and nineteenth centuries and formed one of the strands of the mathematical thread that became modern algebra in the early twentieth century. Another emerged from attempts to understand the general behavior of systems of (one or more) polynomials in n unknowns, and yet another grew from efforts to approach number-theoretic questions algebraically.
6 The Search for the Roots of Algebraic Equations
The problem of finding roots of polynomials provides a direct link from the algebra of the high school classroom to that of the modern research mathematician. Today’s high school student dutifully employs the quadratic formula to calculate the roots of second-degree polynomials. To derive this formula, one transforms the given polynomial into one that can be solved more easily. By more complicated manipulations of cubics and quartics, Cardano and Ferrari obtained formulas for the roots of those as well. It is natural to ask whether the same can be done for higher-degree polynomials. More precisely, are there formulas that involve just the usual operations of arithmetic—addition, subtraction, multiplication, and division—together with the extraction of roots? When there is such a formula, one says that the equation is solvable by radicals.
Although many eighteenth-century mathematicians (including Euler, Alexandre-Théophile Vandermonde (1735–96), WARING [VI.21], and Étienne Bézout (1730–83)) contributed to the effort to decide whether higher-order polynomial equations are solvable by radicals, it was not until the years from roughly 1770 to 1830 that there were significant breakthroughs, particularly in the work of LAGRANGE [VI.22], ABEL [VI.33], and Gauss.
In a lengthy set of “Réflections sur la résolution algébrique des équations” (Reflections on the algebraic resolution of equations) published in 1771, Lagrange tried to determine principles underlying the resolution of algebraic equations in general by analyzing in detail the specific cases of the cubic and the quartic. Building on the work of Cardano, Lagrange showed that a cubic of the form x3 + ax2 + bx + c = 0 could always be transformed into a cubic with no quadratic term x3 + px + q = 0 and that the roots of this could be written as x = u + v, where u3 and v3 are the roots of a certain quadratic polynomial equation. Lagrange was then able to show that if x1, x2, x3 are the three roots of the cubic, the intermediate functions u and v could actually be written as u = 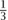 (x1 + αx2 + α2x3) and v =
(x1 + αx2 + α2x3) and v = 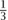 (x1 + α2x2 + αx3), for α a primitive cube root of unity. That is, u and v could be written as rational expressions or resolvents in xl, x2, x3. Conversely, starting with a linear expression y = Ax1 + Bx2 + Cx3 in the roots xl, x2, x3 and then permuting the roots in all possible ways yielded six expressions each of which was a root of a particular sixth-degree polynomial equation. An analysis of the latter equation (which involved the exploitation of properties of symmetric polynomials) yielded the same expressions for u and v in terms of x1, x2, x3 and the cube root of unity α. As Lagrange showed, this kind of two-pronged analysis—involving intermediate expressions rational in the roots that are solutions of a solvable equation as well as the behavior of certain rational expressions under permutation of the roots—yielded the complete solution in the cases both of the cubic and the quartic. It was one approach that encompassed the solution of both types of equation. But could this technique be extended to the case of the quintic and higher-degree polynomials? Lagrange was unable to push it through in the case of the quintic, but by building on his ideas, first his student Paolo Ruffini (1765–1822) at the turn of the nineteenth century and then, definitively, the young Norwegian mathematician Abel in the 1820s showed that, in fact, the quintic is not solvable by radicals. (See THE INSOLUBILITY OF THE QUINTIC [V.21].) This negative result, however, still left open the questions of which algebraic equations were solvable by radicals and why.
(x1 + α2x2 + αx3), for α a primitive cube root of unity. That is, u and v could be written as rational expressions or resolvents in xl, x2, x3. Conversely, starting with a linear expression y = Ax1 + Bx2 + Cx3 in the roots xl, x2, x3 and then permuting the roots in all possible ways yielded six expressions each of which was a root of a particular sixth-degree polynomial equation. An analysis of the latter equation (which involved the exploitation of properties of symmetric polynomials) yielded the same expressions for u and v in terms of x1, x2, x3 and the cube root of unity α. As Lagrange showed, this kind of two-pronged analysis—involving intermediate expressions rational in the roots that are solutions of a solvable equation as well as the behavior of certain rational expressions under permutation of the roots—yielded the complete solution in the cases both of the cubic and the quartic. It was one approach that encompassed the solution of both types of equation. But could this technique be extended to the case of the quintic and higher-degree polynomials? Lagrange was unable to push it through in the case of the quintic, but by building on his ideas, first his student Paolo Ruffini (1765–1822) at the turn of the nineteenth century and then, definitively, the young Norwegian mathematician Abel in the 1820s showed that, in fact, the quintic is not solvable by radicals. (See THE INSOLUBILITY OF THE QUINTIC [V.21].) This negative result, however, still left open the questions of which algebraic equations were solvable by radicals and why.
As Lagrange’s analysis seemed to underscore, the answer to this question in the cases of the cubic and the quartic involved in a critical way the cube and fourth roots of unity, respectively. By definition, these satisfy the particularly simple polynomial equations x3 - 1 = 0 and x4 - 1 = 0, respectively. It was thus natural to examine the general case of the so-called cyclotomic equation xn - 1 = 0 and ask for what values n the nth roots of unity are actually constructible. To put this question in equivalent algebraic terms: for which n is it possible to find a formula for the nth roots of unity that expresses them in terms of integers using the usual arithmetical operations and extraction of square (but not higher) roots? This was one of the many questions explored by Gauss in his wide-ranging, magisterial, and groundbreaking 1801 treatise Disquisitiones Arithmeticae. One of his most famous results was that the regular 17-gon (or, equivalently, a 17th root of unity) was constructible. In the course of his analysis, he not only employed techniques similar to those developed by Lagrange but also developed key concepts such as MODULAR ARITHMETIC [III.58] and the properties of the modular “worlds” ℤp, for p a prime, and, more generally, ℤn, for n  ℤ+, as well as the notion of a primitive element (a generator) of what would later be termed a cyclic group.
ℤ+, as well as the notion of a primitive element (a generator) of what would later be termed a cyclic group.
Although it is not clear how well he knew Gauss’s work, in the years around 1830 GALOIS [VI.41] drew from the ideas both of Lagrange on the analysis of resolvents and of CAUCHY [VI.29] on permutations and substitutions to obtain a solution to the general problem of solvability of polynomial equations by radicals. Although his approach borrowed from earlier ideas, it was in one important respect fundamentally new. Whereas prior efforts had aimed at deriving an explicit algorithm for calculating the roots of a polynomial of a given degree, Galois formulated a theoretical process based on constructs more general than but derived from the given equation that allowed him to assess whether or not that equation was solvable.
To be more precise, Galois recast the problem into one in terms of two new concepts: fields (which he called “domains of rationality”) and groups (or, more precisely, groups of substitutions). A polynomial equation f(x) = 0 of degree n was reducible over its domain of rationality—the ground field from which its coefficients were taken—if all n of its roots were in that ground field; otherwise, it was irreducible over that field. It could, however, be reducible over some larger field. Consider, for example, the polynomial x2 + 1 as a polynomial over ℝ, the field of real numbers. While we know from high school algebra that this polynomial does not factor into a product of two real, linear factors (that is, there are no real numbers rl and r2 such that x2 + 1 = (x - r1)(x - r2)), it does factor over ℂ, the field of complex numbers, and, specifically, x2 + 1 = (x +  )(x -
)(x -  ). Thus, if we take all numbers of the form a + b
). Thus, if we take all numbers of the form a + b , where a and b belong to ℝ, then we enlarge ℝ to a new field ℂ in which the polynomial x2 + 1 is reducible. If
, where a and b belong to ℝ, then we enlarge ℝ to a new field ℂ in which the polynomial x2 + 1 is reducible. If  is a field and x is an element of
is a field and x is an element of  that does not have an nth root in
that does not have an nth root in  , then by a similar process we can adjoin an element y to
, then by a similar process we can adjoin an element y to  and stipulate that yn = x. We call y a radical. The set of all polynomial expressions in y, with coefficients in
and stipulate that yn = x. We call y a radical. The set of all polynomial expressions in y, with coefficients in  , can be shown to form a larger field. Galois showed that if it was possible to enlarge
, can be shown to form a larger field. Galois showed that if it was possible to enlarge  by successively adjoining radicals to obtain a field K in which f(x) factored into n linear factors, then f(x) = 0 was solvable by radicals. He developed a process that hinged both on the notion of adjoining an element—in particular, a so-called primitive element—to a given ground field and on the idea of analyzing the internal structure of this new, enlarged field via an analysis of the (finite) group of substitutions (automorphisms of K) that leave invariant all rational relations of the n roots of f(x) = 0. The group-theoretic aspects of Galois’s analysis were particularly potent; he introduced the notions, although not the modern terminology, of a normal subgroup of a group, a factor group, and a solvable group. Galois thus resolved the concrete problem of determining when a polynomial equation was solvable by radicals by examining it from the abstract perspective of groups and their internal structure.
by successively adjoining radicals to obtain a field K in which f(x) factored into n linear factors, then f(x) = 0 was solvable by radicals. He developed a process that hinged both on the notion of adjoining an element—in particular, a so-called primitive element—to a given ground field and on the idea of analyzing the internal structure of this new, enlarged field via an analysis of the (finite) group of substitutions (automorphisms of K) that leave invariant all rational relations of the n roots of f(x) = 0. The group-theoretic aspects of Galois’s analysis were particularly potent; he introduced the notions, although not the modern terminology, of a normal subgroup of a group, a factor group, and a solvable group. Galois thus resolved the concrete problem of determining when a polynomial equation was solvable by radicals by examining it from the abstract perspective of groups and their internal structure.
Galois’s ideas, although sketched in the early 1830s, did not begin to enter into the broader mathematical consciousness until their publication in 1846 in LIOUVILLE’S [VI.39] Journal des Mathématiques Pures et Appliquées, and they were not fully appreciated until two decades later when first Joseph Serret (1819–85) and then JORDAN [VI.52] fleshed them out more fully. In particular, Jordan’s Traité des Substitutions et des Équations Algébriques (“Treatise on substitutions and on algebraic equations”) of 1870 not only highlighted Galois’s work on the solution of algebraic equations but also developed the general structure theory of permutation groups as it had evolved at the hands of Lagrange, Gauss, Cauchy, Galois, and others. By the end of the nineteenth century, this line of development of group theory, stemming from efforts to solve algebraic equations by radicals, had intertwined with three others: the abstract notion of a group defined in terms of a group multiplication table, which was formulated by CAYLEY [VI.46], the structural work of mathematicians like Ludwig Sylow (1832–1918) and Otto Hölder (1859–1937), and the geometrical work of LIE [VI.53] and KLEIN [VI.57]. By 1893, when Heinrich Weber (1842–1914) codified much of this earlier work by giving the first actual abstract definitions of the notions both of group and field, thereby recasting them in a form much more familiar to the modern mathematician, groups and fields had been shown to be of central importance in a wide variety of areas, both mathematical and physical.
7 Exploring the Behavior of Polynomials in n Unknowns
The problem of solving algebraic equations involved finding the roots of polynomials in one unknown. At least as early as the late seventeenth century, however, mathematicians like LEIBNIZ [VI.15] had been interested in techniques for solving simultaneously systems of linear equations in more than two variables. Although his work remained unknown at the time, Leibniz considered three linear equations in three unknowns and determined their simultaneous solvability based on the value of a particular expression in the coefficients of the system. This expression, equivalent to what Cauchy would later call the DETERMINANT [III.15] and which would ultimately be associated with an n × n square array or MATRIX [I.3 §4.2] of coefficients, was also developed and analyzed independently by Gabriel Cramer (1704–52) in the mid eighteenth century in the general context of the simultaneous solution of a system of n linear equations in n unknowns. From these beginnings, a theory of determinants, independent of the context of solving systems of linear equations, quickly became a topic of algebraic study in its own right, attracting the attention of Vandermonde, LAPLACE [VI.23], and Cauchy, among others. Determinants were thus an example of a new algebraic construct, the properties of which were then systematically explored.
Although determinants came to be viewed in terms of what SYLVESTER [VI.42] would dub matrices, a theory of matrices proper grew initially from the context not of solving simultaneous linear equations but rather of linearly transforming the variables of homogeneous polynomials in two, three, or more generally n variables. In the Disquisitiones Arithmeticae, for example, Gauss considered how binary and ternary quadratic forms with integer coefficients—expressions of the form a1x2 + 2a2xy + a3y2 and a1x2 + a2y2 + a3z2 + 2a4xy + 2a5xz + 2a6yz, respectively—are affected by a linear transformation of their variables. In the ternary case, he applied the linear transformation x = αx′ + βy′ + γz′, y = α′x′ + β′y′ + γ′z′, and z = α″x′ + β″y′ + γ″z′ to derive a new ternary form. He denoted the linear transformation of the variables by the square array
α, β, γ
α′, β′, γ′
α″, β″, γ″
and, in the process of showing what the composition of two such transformations was, gave an explicit example of matrix multiplication. By the middle of the nineteenth century, Cayley had begun to explore matrices per se and had established many of the properties that the theory of matrices as a mathematical system in its own right enjoys. This line of algebraic thought was eventually reinterpreted in terms of the theory of algebras (see below) and developed into the independent area of linear algebra and the theory of VECTOR SPACES [I.3 §2.3].
Another theory that arose out of the analysis of linear transformations of homogeneous polynomials was the theory of invariants, and this too has its origins in some sense in Gauss’s Disquisitiones. As in his study of ternary quadratic forms, Gauss began his study of binary forms by applying a linear transformation, specifically, x = αx′ + βy′, y = γx′ + δy′. The result was the new binary form 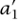 (x′)2 + 2
(x′)2 + 2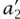 x′y′ +
x′y′ + 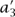 (y′)2, where, explicitly,
(y′)2, where, explicitly, 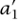 = a1α2 + 2a2αγ + a3γ2,
= a1α2 + 2a2αγ + a3γ2, 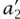 = a1αβ + a2(αδ + βγ) + a3γδ, and
= a1αβ + a2(αδ + βγ) + a3γδ, and 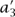 = a1β2 + 2a2βδ + a3δ2. As Gauss noted, if you multiply the second of these equations by itself and subtract from this the product of the first and the third equations, you obtain the relation
= a1β2 + 2a2βδ + a3δ2. As Gauss noted, if you multiply the second of these equations by itself and subtract from this the product of the first and the third equations, you obtain the relation 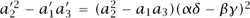 . To use language that Sylvester would develop in the early 1850s, Gauss realized that the expression
. To use language that Sylvester would develop in the early 1850s, Gauss realized that the expression 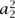 - a1a3 in the coefficients of the original binary quadratic form is an invariant in the sense that it remains unchanged up to a power of the determinant of the linear transformation. By the time Sylvester coined the term, the invariant phenomenon had also appeared in the work of the English mathematician BOOLE [VI.43], and had attracted Cayley’s attention. It was not until after Cayley and Sylvester met in the late 1840s, however, that the two of them began to pursue a theory of invariants proper, which aimed to determine all invariants for homogeneous polynomials of degree m in n unknowns as well as simultaneous invariants for systems of such polynomials.
- a1a3 in the coefficients of the original binary quadratic form is an invariant in the sense that it remains unchanged up to a power of the determinant of the linear transformation. By the time Sylvester coined the term, the invariant phenomenon had also appeared in the work of the English mathematician BOOLE [VI.43], and had attracted Cayley’s attention. It was not until after Cayley and Sylvester met in the late 1840s, however, that the two of them began to pursue a theory of invariants proper, which aimed to determine all invariants for homogeneous polynomials of degree m in n unknowns as well as simultaneous invariants for systems of such polynomials.
Although Cayley and (especially) Sylvester pursued this line of research from a purely algebraic point of view, invariant theory also had number-theoretic and geometric implications, the former explored by Gotthold Eisenstein (1823–52) and HERMITE [VI.47], the latter by Otto Hesse (1811–74), Paul Gordan (1837–1912), and Alfred Clebsch (1833–72), among others. It was of particular interest to understand how many “genuinely distinct” invariants were associated with a specific form, or system of forms. In 1868, Gordan achieved a fundamental breakthrough by showing that the invariants associated with any binary form in n variables can always be expressed in terms of a finite number of them. By the late 1880s and early 1890s, however, HILBERT [VI.63] brought new, abstract concepts associated with the theory of algebras (see below) to bear on invariant theory and, in so doing, not only reproved Gordan’s result but also showed that the result was true for forms of degree m in n unknowns. With Hilbert’s work, the emphasis shifted from the concrete calculations of his English and German predecessors to the kind of structurally oriented existence theorems that would soon be associated with abstract, modern algebra.
8 The Quest to Understand the Properties of “Numbers”
As early as the sixth century B.C.E., the Pythagoreans had studied the properties of numbers formally. For example, they defined the concept of a perfect number, which is a positive integer, such as 6 = 1 + 2 + 3 and 28 = 1 + 2 + 4 + 7 + 14, which is the sum of its divisors (excluding the integer itself). In the sixteenth century, Cardano and Bombelli had willingly worked with new expressions, complex numbers, of the form a + 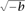 for real numbers a and b, and had explored their computational properties. In the seventeenth century, Fermat famously claimed that he could prove that the equation xn + yn = zn, for n an integer greater than 2, had no solutions in the integers, except for the trivial cases when z = x or z = y and the remaining variable is zero. The latter result, known as FERMAT’S LAST THEOREM [V.10], generated many new ideas, especially in the eighteenth and nineteenth centuries, as mathematicians worked to find an actual proof of Fermat’s claim. Central to their efforts were the creation and algebraic analysis of new types of number systems that extended the integers in much the same way that Galois had extended fields. This flexibility to create and analyze new number systems was to become one of the hallmarks of modern algebra as it would develop into the twentieth century.
for real numbers a and b, and had explored their computational properties. In the seventeenth century, Fermat famously claimed that he could prove that the equation xn + yn = zn, for n an integer greater than 2, had no solutions in the integers, except for the trivial cases when z = x or z = y and the remaining variable is zero. The latter result, known as FERMAT’S LAST THEOREM [V.10], generated many new ideas, especially in the eighteenth and nineteenth centuries, as mathematicians worked to find an actual proof of Fermat’s claim. Central to their efforts were the creation and algebraic analysis of new types of number systems that extended the integers in much the same way that Galois had extended fields. This flexibility to create and analyze new number systems was to become one of the hallmarks of modern algebra as it would develop into the twentieth century.
One of the first to venture down this path was Euler. In the proof of Fermat’s last theorem for the n = 3 case that he gave in his Elements of Algebra of 1770, Euler introduced the system of numbers of the form a + b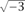 , where a and b are integers. He then blithely proceeded to factorize them into primes, without further justification, just as he would have factorized ordinary integers. By the 1820s and 1830s, Gauss had launched a more systematic study of numbers that are now called the Gaussian integers. These are all numbers of the form a + b
, where a and b are integers. He then blithely proceeded to factorize them into primes, without further justification, just as he would have factorized ordinary integers. By the 1820s and 1830s, Gauss had launched a more systematic study of numbers that are now called the Gaussian integers. These are all numbers of the form a + b , for integers a and b. He showed that, like the integers, the Gaussian integers are closed under addition, subtraction, and multiplication; he defined the notions of unit, prime, and norm in order to prove an analogue of THE FUNDAMENTAL THEOREM OF ARITHMETIC [V.14] for them. He thereby demonstrated that there were whole new algebraic worlds to create and explore. (See ALGEBRAIC NUMBERS [IV.1] for more on these topics.)
, for integers a and b. He showed that, like the integers, the Gaussian integers are closed under addition, subtraction, and multiplication; he defined the notions of unit, prime, and norm in order to prove an analogue of THE FUNDAMENTAL THEOREM OF ARITHMETIC [V.14] for them. He thereby demonstrated that there were whole new algebraic worlds to create and explore. (See ALGEBRAIC NUMBERS [IV.1] for more on these topics.)
Whereas Euler had been motivated in his work by Fermat’s last theorem, Gauss was trying to generalize the LAW OF QUADRATIC RECIPROCITY [V.28] to a law of biquadratic reciprocity. In the quadratic case, the problem was the following. If a and m are integers with m ≥ 2, then we say that a is a quadratic residue mod m if the equation x2 = a has a solution mod m; that is, if there is an integer x such that x2 is congruent to a mod m. Now suppose that p and q are distinct odd primes. If you know whether p is a quadratic residue mod q, is there a simple way of telling whether q is a quadratic residue mod p? In 1785, Legendre had posed and answered this question—the status of q mod p will be the same as that of p mod q if at least one of p and q is congruent to 1 mod 4, and different if they are both congruent to 3 mod 4—but he had given a faulty proof. By 1796, Gauss had come up with the first rigorous proof of the theorem (he would ultimately give eight different proofs of it), and by the 1820s he was asking the analogous question for the case of two biquadratic equivalences x4 ≡ p (mod q) and y4 ≡ q (mod p). It was in his attempts to answer this new question that he introduced the Gaussian integers and signaled at the same time that the theory of residues of higher degrees would make it necessary to create and analyze still other new sorts of “integers.” Although Eisenstein, DIRICHLET [VI.36], Hermite, KUMMER [VI.40], and KRONECKER [VI.48], among others, pushed these ideas forward in this Gaussian spirit, it was DEDEKIND [VI.50] in his tenth supplement to Dirichlet’s Vorlesungen über Zahlentheorie (Lectures on Number Theory) of 1871 who fundamentally reconceptualized the problem by treating it not number theoretically but rather set theoretically and axiomatically. Dedekind introduced, for example, the general notions—if not what would become the precise axiomatic definitions—of fields, rings, IDEALS [III.81 §2], and MODULES [III.81 §3] and analyzed his number-theoretic setting in terms of these new, abstract constructs. His strategy was, from a philosophical point of view, not unlike that of Galois: translate the “concrete” problem at hand into new, more abstract terms in order to solve it more cleanly at a “higher” level. In the early twentieth century, NOETHER [VI.76] and her students, among them Bartel van der Waerden (1903–96), would develop Dedekind’s ideas further to help create the structural approach to algebra so characteristic of the twentieth century.
Parallel to this nineteenth-century, number-theoretic evolution of the notion of “number” on the continent of Europe, a very different set of developments was taking place, initially in the British Isles. From the late eighteenth century, British mathematicians had debated not only the nature of number—questions such as, “Do negative and imaginary numbers make sense?”—but also the meaning of algebra—questions like, “In an expression like ax + by, what values may a, b, x, and y legitimately take on and what precisely may ‘+’ connote?” By the 1830s, the Irish mathematician HAMILTON [VI.37] had come up with a “unified” interpretation of the complex numbers that circumvented, in his view, the logical problem of adding a real number and an imaginary one, an apple and an orange. Given real numbers a and b, Hamilton conceived of the complex number a + b as the ordered pair (he called it a “couple”) (a, b). He then defined addition, subtraction, multiplication, and division of such couples. As he realized, this also provided a way of representing numbers in the complex plane, and so he naturally asked whether he could construct algebraic, ordered triples so as to represent points in 3-space. After a decade of contemplating this question off and on, Hamilton finally answered it not for triples but for quadruples, the so-called QUATERNIONS [III.76], “numbers” of the form (a, b, c, d) = a+bi+cj+dk, where a, b, c, and d are real and where i, j, k satisfy the relations ij = -ji = k, jk = -kj = i, ki = -ik = j, i2 = j2 = k2 = -1. As in the two-dimensional case, addition is defined component-wise, but multiplication, while definable in such a way that every nonzero element has a multiplicative inverse, is not commutative. Thus, this new number system did not obey all of the “usual” laws of arithmetic.
as the ordered pair (he called it a “couple”) (a, b). He then defined addition, subtraction, multiplication, and division of such couples. As he realized, this also provided a way of representing numbers in the complex plane, and so he naturally asked whether he could construct algebraic, ordered triples so as to represent points in 3-space. After a decade of contemplating this question off and on, Hamilton finally answered it not for triples but for quadruples, the so-called QUATERNIONS [III.76], “numbers” of the form (a, b, c, d) = a+bi+cj+dk, where a, b, c, and d are real and where i, j, k satisfy the relations ij = -ji = k, jk = -kj = i, ki = -ik = j, i2 = j2 = k2 = -1. As in the two-dimensional case, addition is defined component-wise, but multiplication, while definable in such a way that every nonzero element has a multiplicative inverse, is not commutative. Thus, this new number system did not obey all of the “usual” laws of arithmetic.
Although some of Hamilton’s British contemporaries questioned the extent to which mathematicians were free to create such new mathematical worlds, others, like Cayley, immediately took the idea further and created a system of ordered 8-tuples, the octonions, the multiplication of which was neither commutative nor even, as was later discovered, associative. Several questions naturally arise about such systems, but one that Hamilton asked was what happens if the field of coefficients, the base field, is not the reals but rather the complexes? In that case, it is easy to see that the product of the two nonzero complex quaternions (- ,0,1,0) = -
,0,1,0) = - +j and (
+j and ( ,0,1,0) =
,0,1,0) =  +j is 1 + j2 = 1 + (-1) = 0. In other words, the complex quaternions contain zero divisors—nonzero elements the product of which is zero—another phenomenon that distinguishes their behavior fundamentally from that of the integers. As it flourished in the hands of mathematicians like Benjamin Peirce (1809–80), FROBENIUS [VI.58], Georg Scheffers (1866–1945), Theodor Molien (1861–1941), CARTAN [VI.69], and Joseph H. M. Wedderburn (1882–1948), among others, this line of thought resulted in a freestanding theory of algebras. This naturally intertwined with developments in the theory of matrices (the n × n matrices form an algebra of dimension n2 over their base field) as it had evolved through the work of Gauss, Cayley, and Sylvester. It also merged with the not unrelated theory of n-dimensional vector spaces (n-dimensional algebras are n-dimensional vector spaces with a vector multiplication as well as a vector addition and scalar multiplication) that issued from ideas like those of Hermann Grassmann (1809–77).
+j is 1 + j2 = 1 + (-1) = 0. In other words, the complex quaternions contain zero divisors—nonzero elements the product of which is zero—another phenomenon that distinguishes their behavior fundamentally from that of the integers. As it flourished in the hands of mathematicians like Benjamin Peirce (1809–80), FROBENIUS [VI.58], Georg Scheffers (1866–1945), Theodor Molien (1861–1941), CARTAN [VI.69], and Joseph H. M. Wedderburn (1882–1948), among others, this line of thought resulted in a freestanding theory of algebras. This naturally intertwined with developments in the theory of matrices (the n × n matrices form an algebra of dimension n2 over their base field) as it had evolved through the work of Gauss, Cayley, and Sylvester. It also merged with the not unrelated theory of n-dimensional vector spaces (n-dimensional algebras are n-dimensional vector spaces with a vector multiplication as well as a vector addition and scalar multiplication) that issued from ideas like those of Hermann Grassmann (1809–77).
9 Modern Algebra
By 1900, many new algebraic structures had been identified and their properties explored. Structures that were first isolated in one context were then found to appear, sometimes unexpectedly, in others: thus, these new structures were mathematically more general than the problems that had led to their discovery. In the opening decades of the twentieth century, algebraists (the term is not ahistorical by 1900) increasingly recognized these commonalities—these shared structures such as groups, fields and rings—and asked questions at a more abstract level. For example, what are all of the finite simple groups? Can they be classified? (See THE CLASSIFICATION OF FINITE SIMPLE GROUPS [V.7].) Moreover, inspired by the set-theoretic and axiomatic work of CANTOR [VI.54], Hilbert, and others, they came to appreciate the common standard of analysis and comparison that axiomatization could provide. Coming from this axiomatic point of view, Ernst Steinitz (1871–1928), for example, laid the groundwork for an abstract theory of fields in 1910, while Abraham Fraenkel (1891–1965) did the same for an abstract theory of rings four years later. As van der Waerden came to realize in the late 1920s, these developments could be interpreted as dovetailing philosophically with results like Hilbert’s in invariant theory and Dedekind’s and Noether’s in the algebraic theory of numbers. That interpretation, laid out in 1930 in van der Waerden’s classic textbook Moderne Algebra, codified the structurally oriented “modern algebra” that subsumed the algebra of polynomials of the high school classroom and that continues to characterize algebraic thought today.
Further Reading
Bashmakova, I., and G. Smirnova. 2000. The Beginnings and Evolution of Algebra, translated by A. Shenitzer. Washington, DC: The Mathematical Association of America.
Corry, L. 1996. Modern Algebra and the Rise of Mathematical Structures. Science Networks, volume 17. Basel: Birkhäuser.
Edwards, H. M. 1984. Galois Theory. New York: Springer.
Heath, T. L. 1956. The Thirteen Books of Euclid’s Elements, 2nd edn. (3 vols.). New York: Dover.
Høyrup, J. 2002. Lengths, Widths, Surfaces: A Portrait of Old Babylonian Algebra and Its Kin. New York: Springer.
Klein, J. 1968. Greek Mathematical Thought and the Origin of Algebra, translated by E. Brann. Cambridge, MA: The MIT Press.
Netz, R. 2004. The Transformation of Mathematics in the Early Mediterranean World: From Problems to Equations. Cambridge: Cambridge University Press.
Parshall, K. H. 1988. The art of algebra from al-Khw rizm
rizm to Viète: A study in the natural selection of ideas. History of Science 26:129–64.
to Viète: A study in the natural selection of ideas. History of Science 26:129–64.
—. 1989. Toward a history of nineteenth-century invariant theory. In The History of Modern Mathematics, edited by D. E. Rowe and J. McCleary, volume 1, pp. 157–206. Amsterdam: Academic Press.
Sesiano, J. 1999. Une Introduction à l’histoire de l’algèbre: Résolution des équations des Mésopotamiens à la Renaissance. Lausanne: Presses Polytechniques et Universitaires Romandes.
Van der Waerden, B. 1985. A History of Algebra from al-Khw rizm
rizm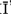 to Emmy Noether. New York: Springer.
to Emmy Noether. New York: Springer.
Wussing, H. 1984. The Genesis of the Abstract Group Concept:A Contribution to the History of the Origin of Abstract Group Theory, translated by A. Shenitzer. Cambridge, MA: The MIT Press.
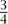 , where it is important to notice that the Babylonian number system is base 60, so 45' denotes
, where it is important to notice that the Babylonian number system is base 60, so 45' denotes 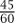 =
= 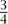 . The text then lays out the following algorithm for solving the problem: take 1, the coefficient of the linear term, and halve it to get
. The text then lays out the following algorithm for solving the problem: take 1, the coefficient of the linear term, and halve it to get  . Square
. Square  to get
to get 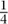 . Add
. Add 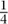 to
to 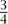 , the constant term, to get 1. This is the square of 1. Subtract from this the
, the constant term, to get 1. This is the square of 1. Subtract from this the  which you multiplied by to get
which you multiplied by to get  , the side of the square. The modern reader can easily see that this algorithm is equivalent to what is now called the quadratic formula, but the Babylonian tablet presents it in the context of a particular problem and repeats it in the contexts of other particular problems. There are no equations in the modern sense; the Babylonian writer is literally effecting a construction of plane figures. Similar problems and similar algorithmic solutions can also be found in ancient Egyptian texts such as the Rhind papyrus, believed to have been copied in 1650 B.C.E. from a text that was about a century and a half older.
, the side of the square. The modern reader can easily see that this algorithm is equivalent to what is now called the quadratic formula, but the Babylonian tablet presents it in the context of a particular problem and repeats it in the contexts of other particular problems. There are no equations in the modern sense; the Babylonian writer is literally effecting a construction of plane figures. Similar problems and similar algorithmic solutions can also be found in ancient Egyptian texts such as the Rhind papyrus, believed to have been copied in 1650 B.C.E. from a text that was about a century and a half older.
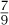 gave him what he needed, so a solution was
gave him what he needed, so a solution was 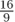 ,
, 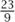 ,
, 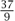 , and he was done. He provided no geometrical justification because in his view none was needed; a single numerical solution was all he required. He did not set up what we would recognize as a more general set of equations and try to find all possible solutions.
, and he was done. He provided no geometrical justification because in his view none was needed; a single numerical solution was all he required. He did not set up what we would recognize as a more general set of equations and try to find all possible solutions. RIZM
RIZM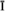 [VI.5] was a scholar at the royally funded House of Wisdom in Baghdad. He linked the kinds of geometrical arguments Euclid had presented in Book II of his Elements with the indigenous problemsolving algorithms that dated back to Old Babylonian times. In particular, he wrote a book on practical mathematics, entitled al-Kit
[VI.5] was a scholar at the royally funded House of Wisdom in Baghdad. He linked the kinds of geometrical arguments Euclid had presented in Book II of his Elements with the indigenous problemsolving algorithms that dated back to Old Babylonian times. In particular, he wrote a book on practical mathematics, entitled al-Kit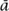 b al-mukhtasar f
b al-mukhtasar f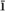 his
his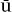 K
K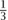 (x1 + αx2 + α2x3) and v =
(x1 + αx2 + α2x3) and v =  ℤ+, as well as the notion of a primitive element (a generator) of what would later be termed a cyclic group.
ℤ+, as well as the notion of a primitive element (a generator) of what would later be termed a cyclic group. )(x -
)(x -  is a field and x is an element of
is a field and x is an element of 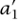 (x′)2 + 2
(x′)2 + 2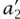 x′y′ +
x′y′ + 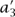 (y′)2, where, explicitly,
(y′)2, where, explicitly, 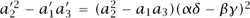 . To use language that Sylvester would develop in the early 1850s, Gauss realized that the expression
. To use language that Sylvester would develop in the early 1850s, Gauss realized that the expression 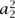 - a1a3 in the coefficients of the original binary quadratic form is an invariant in the sense that it remains unchanged up to a power of the determinant of the linear transformation. By the time Sylvester coined the term, the invariant phenomenon had also appeared in the work of the English mathematician BOOLE [VI.43], and had attracted Cayley’s attention. It was not until after Cayley and Sylvester met in the late 1840s, however, that the two of them began to pursue a theory of invariants proper, which aimed to determine all invariants for homogeneous polynomials of degree m in n unknowns as well as simultaneous invariants for systems of such polynomials.
- a1a3 in the coefficients of the original binary quadratic form is an invariant in the sense that it remains unchanged up to a power of the determinant of the linear transformation. By the time Sylvester coined the term, the invariant phenomenon had also appeared in the work of the English mathematician BOOLE [VI.43], and had attracted Cayley’s attention. It was not until after Cayley and Sylvester met in the late 1840s, however, that the two of them began to pursue a theory of invariants proper, which aimed to determine all invariants for homogeneous polynomials of degree m in n unknowns as well as simultaneous invariants for systems of such polynomials.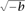 for real numbers a and b, and had explored their computational properties. In the seventeenth century, Fermat famously claimed that he could prove that the equation xn + yn = zn, for n an integer greater than 2, had no solutions in the integers, except for the trivial cases when z = x or z = y and the remaining variable is zero. The latter result, known as FERMAT’S LAST THEOREM [V.10], generated many new ideas, especially in the eighteenth and nineteenth centuries, as mathematicians worked to find an actual proof of Fermat’s claim. Central to their efforts were the creation and algebraic analysis of new types of number systems that extended the integers in much the same way that Galois had extended fields. This flexibility to create and analyze new number systems was to become one of the hallmarks of modern algebra as it would develop into the twentieth century.
for real numbers a and b, and had explored their computational properties. In the seventeenth century, Fermat famously claimed that he could prove that the equation xn + yn = zn, for n an integer greater than 2, had no solutions in the integers, except for the trivial cases when z = x or z = y and the remaining variable is zero. The latter result, known as FERMAT’S LAST THEOREM [V.10], generated many new ideas, especially in the eighteenth and nineteenth centuries, as mathematicians worked to find an actual proof of Fermat’s claim. Central to their efforts were the creation and algebraic analysis of new types of number systems that extended the integers in much the same way that Galois had extended fields. This flexibility to create and analyze new number systems was to become one of the hallmarks of modern algebra as it would develop into the twentieth century.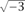 , where a and b are integers. He then blithely proceeded to factorize them into primes, without further justification, just as he would have factorized ordinary integers. By the 1820s and 1830s, Gauss had launched a more systematic study of numbers that are now called the Gaussian integers. These are all numbers of the form a + b
, where a and b are integers. He then blithely proceeded to factorize them into primes, without further justification, just as he would have factorized ordinary integers. By the 1820s and 1830s, Gauss had launched a more systematic study of numbers that are now called the Gaussian integers. These are all numbers of the form a + b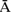 rizm
rizm to Viète: A study in the natural selection of ideas. History of Science 26:129–64.
to Viète: A study in the natural selection of ideas. History of Science 26:129–64.