In many respects the development of the idea of proof is coextensive with the development of mathematics as a whole. Looking back into the past, one might at first consider mathematics to be a body of scientific knowledge that deals with the properties of numbers, magnitudes, and figures, obtaining its justifications from proofs rather than, say, from experiments or inductive inferences. Such a characterization, however, is not without problems. For one thing, it immediately leaves out important chapters in the history of civilization that are more naturally associated with mathematics than with any other intellectual activity. For example, the Mesopotamian and Egyptian cultures developed elaborate bodies of knowledge that would most naturally be described as belonging to arithmetic or geometry, even though nothing is found in them that comes close to the idea of proof as it was later practiced in mathematics at large. To the extent that any justification is given, say, in the thousands of mathematical procedures found on clay tablets written in cuneiform script, it is inductive or based on experience. The tablets repetitively show—without additional explanation or attempts at general justifications—a given procedure to be followed whenever one is pursuing a certain type of result. Later on, in the context of Chinese, Japanese, Mayan, or Hindu cultures, one again finds important developments in fields naturally associated with mathematics. The extent to which these cultures pursued the idea of mathematical proof—a question that is debated among historians to this day—was undoubtedly not as great as it was in Greek tradition, and it certainly did not take the specific forms we typically associate with the latter. Should one nevertheless say that these are instances of mathematical knowledge, even though they are not justified on the basis of some kind of general, deductive proof? If so, then we cannot characterize mathematics as a body of knowledge that is backed up by proofs, as suggested above. However, this litmus test certainly provides a useful criterion—one that we do not want to give up too easily—for distinguishing mathematics from other intellectual endeavors.
Without totally ignoring these important questions, the present account focuses on a story that started, at some point in the past, usually taken to be before or around the fifth century B.C.E. in Greece, with the realization that there was a distinctive body of claims, mainly associated with numbers and with diagrams, whose truth could be and needed to be vindicated in a very special way—namely, by means of a general, deductive argument, or “proof.” Exactly when and how this story began is unclear. Equally unclear are the direct historical sources of such a unique idea. Since the emphasis on the use of logic and reason in constructing an argument was well-entrenched in other spheres of public life in ancient Greece—such as politics, rhetoric, and law—much earlier than the fifth century B.C.E., it is possible that it is in those domains that the origins of mathematical proof are to be found.
The early stages of this story raise additional questions, both historical and methodological. For instance, Thales of Miletus, the first mathematician known by name (though he was also a philosopher and scientist), is reported to have proved several geometric theorems, such as, for instance, that the opposite angles between two intersecting straight lines are equal, or that if two vertices of a triangle are the endpoints of the diameter of a circle and the third is any other point on the circle then the triangle must be right angled. Even if we were to accept such reports at face value, several questions would immediately arise: in what sense can it be asserted that Thales “proved” these results? More specifically, what were Thales’s initial assumptions and what inference methods did he take to be valid? We know very little about this. However, we do know that, as a result of a complex historical process, a certain corpus of knowledge eventually developed that comprised known results, techniques employed, and problems (both solved and yet requiring solution). This corpus gradually also incorporated the regulatory idea of proof: that is, the idea that some kind of general argument, rather than an example (or even many examples), was the necessary justification to be sought in all cases. As part of this development, the idea of proof came to be associated with strictly deductive arguments, as opposed to, say, dialogic (meaning “negotiated”) or “probabilistically inferred” truth. It is an interesting and difficult historical question to establish why this was the case, and one that we will not address here.
EUCLID’S [VI.2] Elements was compiled some time around the year 300 B.C.E. It stands out as the most successful and comprehensive attempt of its kind to organize the basic concepts, results, proofs, and techniques required by anyone wanting to master this increasingly complex body of knowledge. Still, it is important to stress that it was not the only such attempt within the Hellenic world. This endeavor was not just a matter of compilation, codification, and canonization, such as one can find in any other evolving field of learning at any point in time. Instead, the assertions it contained were of two different kinds, and the distinction was vitally important. On the one hand there were basic assumptions, or axioms, and on the other there were theorems, which were typically more elaborate statements, together with accounts of how they followed from the axioms—that is, proofs. The way that proof was conceived and realized in the Elements became the paradigm for centuries to come.
This article outlines the evolution of the idea of deductive proof as initially shaped in the framework of Euclidean-style mathematics and as subsequently practiced in the mainstream mathematical culture of ancient Greece, the Islamic world, Renaissance Europe, early modern European science, and then in the nineteenth century and at the turn of the twentieth. The main focus will be on geometry: other fields like arithmetic and algebra will be treated mainly in relation to it. This choice is amply justified by the subject matter itself. Indeed, much as mathematics stands out among the sciences for the unique way in which it relies on proof, so Euclidean-style geometry stood out—at least until well into the seventeenth century—among closely related disciplines such as arithmetic, algebra, and trigonometry.
Results in these other disciplines, or indeed the disciplines as a whole, were often regarded as fully legitimate only when they had been provided with a geometric (or geometric-like) foundation. However, important developments in nineteenth-century mathematics, mainly in connection with the rise of NON-EUCLIDEAN GEOMETRIES [II.2 §§6–10] and with problems in the FOUNDATIONS OF ANALYSIS [II.5], eventually led to a fundamental change of orientation, where arithmetic (and eventually SET THEORY [IV.22]) became the bastion of certainty and clarity from which other mathematical disciplines, geometry included, drew their legitimacy and their clarity. (See THE CRISIS IN THE FOUNDATIONS OF MATHEMATICS [II.7] for a detailed account of this development.) And yet, even before this fundamental change, Euclidean-style proof was not the only way in which mathematical proof was conceived, explored, and practiced. By focusing mainly on geometry, the present account will necessarily leave out important developments that eventually became the mainstream of legitimate mathematical knowledge. To mention just one important example in this regard, a fundamental question that will not be pursued here is how the principle of mathematical induction originated and developed, became accepted as a legitimate inference rule of universal validity, and was finally codified as one of the basic axioms of arithmetic in the late nineteenth century. Moreover, the evolution of the notion of proof involves many other dimensions that will not be treated here, such as the development of the internal organization of mathematics into subdisciplines, as well as the changing interrelations between mathematics and its neighboring disciplines. At a different level, it is related to how mathematics itself evolved as a socially institutionalized enterprise: we shall not discuss interesting questions about how proofs are produced, made public, disseminated, criticized, and often rewritten and improved.
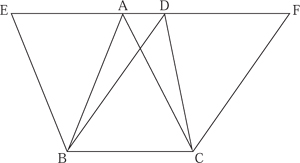
Euclid’s Elements is the paradigmatic work of Greek mathematics, partly for what it has to say about the basic concepts, tools, results, and problems of synthetic geometry and arithmetic, but also for how it regards the role of a mathematical proof and the form that such a proof takes. All proofs appearing in the Elements have six parts and are accompanied by a diagram. I illustrate this with the example of proposition I.37. Euclid’s text is quoted here in the classical translation of Sir Thomas Heath, and the meaning of some terms differs from current usage. Thus, two triangles are said to be “in the same parallels” if they have the same height and both their bases are contained in a single line, and any two figures are said to be “equal” if their areas are equal. For the sake of explanation, names of the parts of the proof have been added: these do not appear in the original. The proof is illustrated in figure 1.
Protasis (enunciation). Triangles which are on the same base and in the same parallels are equal to one another.
Ekthesis (setting out). Let ABC, DBC be triangles on the same base BC and in the same parallels AD, BC.
Diorismos (definition of goal). I say that the triangle ABC is equal to the triangle DBC.
Kataskeue (construction). Let AD be produced in both directions to E, F; through B let BE be drawn parallel to CA, and through C let CF be drawn parallel to BD.
Apodeixis (proof). Then each of the figures EBCA, DBCF is a parallelogram; and they are equal, for they are on the same base BC and in the same parallels BC, EF. Moreover the triangle ABC is half of the parallelogram EBCA, for the diameter AB bisects it; and the triangle DBC is half of the parallelogram DBCF, for the diameter DC bisects it. Therefore the triangle ABC is equal to the triangle DBC.
Sumperasma (conclusion). Therefore triangles which are on the same base and in the same parallels are equal to one another.
This is an example of a proposition that states a property of geometric figures. The Elements also includes propositions that express a task to be carried out. An example is proposition I.1: “On a given finite straight line to construct an equilateral triangle.” The same six parts of the proof and the diagram invariably appear in propositions of this kind as well. This formal structure is also followed in all propositions appearing in the three arithmetic books of the Elements and, most importantly, all of them are always accompanied by a diagram. Thus, for instance, consider proposition IX.35, which in its original version reads as follows:
Figure 1 Proposition I.37 of Euclid’s Elements.
Figure 2 Proposition IX.35 of Euclid’s Elements.
If as many numbers as we please be in continued proportion, and there be subtracted from the second and the last numbers equal to the first, then, as the excess of the second is to the first, so will the excess of the last be to all those before it.
This cumbersome formulation may prove incomprehensible on first reading. In more modern terms, an equivalent to this theorem would state that, given a geometric progression a1, a2, . . . ,an+1, we have
(an+1 - a1) : (a1 + a2 + ... + an) = (a2 - a1) : a1.
This translation, however, fails to convey the spirit of the original, in which no formal symbolic manipulation is, or can be, made. More importantly, a modern algebraic proof fails to convey the ubiquity of diagrams in Greek mathematical proofs, even where they are not needed for a truly geometric construction. Indeed, the accompanying diagram for proposition IX.35 is shown as figure 2 and the first few lines of the proof are as follows:
Let there be as many numbers as we please in continued proportion A, BC, D, EF, beginning from A as least and let there be subtracted from BC and EF the numbers BG, FH, each equal to A; I say that, as GC is to A, so is EH to A, BC, D. For let FK be made equal to BC and FL equal to D. . . .
This proposition and its proof provide good examples of the capabilities, as well as the limitations, of ancient Greek practices of notation, and especially of how they managed without a truly symbolic language. In particular, they demonstrate that proofs were never conceived by the Greeks, even ideally, as purely logical constructs, but rather as specific kinds of arguments that one applied to a diagram. The diagram was not just a visual aid to the argumentation. Rather, through the ekthesis part of the proof, it embodied the idea referred to by the general character and formulation of the proposition.
Together with the centrality of diagrams, the six-part structure is also typical of most of Greek mathematics. The constructions and diagrams that typically appeared in Greek mathematical proofs were not of an arbitrary kind, but what we identify today as straightedge-and-compass constructions. The reasoning in the apodeixis part could be either a direct deduction or an argument by contradiction, but the result was always known in advance and the proof was a means to justify it. In addition, Greek geometric thinking, and in particular Euclid-style geometric proofs, strictly adhered to a principle of homogeneity. That is, magnitudes were only compared with, added to, or subtracted from magnitudes of like kind—numbers, lengths, areas, or volumes. (See NUMBERS [II.1 §2] for more about this.)
Of particular interest are those Greek proofs concerned with lengths of curves, as well as with areas or volumes enclosed by curvilinear shapes. Greek mathematicians lacked a flexible notation capable of expressing the gradual approximation of curves by polygons and an eventual passage to the infinite. Instead, they devised a special kind of proof that involved what can retrospectively be seen as an implicit passage to the limit, but which did so in the framework of a purely geometric proof and thus unmistakably followed the six-part proof-scheme described above. This implicit passage to the infinite was based on the application of a continuity principle, later associated with ARCHIMEDES [VI.3]. In Euclid’s formulation, for instance, the principle states that, given two unequal magnitudes of the same kind, A, B (be they two lengths, two areas, or two volumes), with A greater than B, and if we subtract from A a magnitude which is greater than A/2, and from the remainder we subtract a magnitude that is greater than its half, and if this process is iterated a sufficient number of times, then we will eventually remain with a magnitude that is smaller than B. Euclid used this principle to prove, for instance, that the ratio of the areas of two circles equals the ratio of the squares of their diameters (XII.2). The method used, later known as the exhaustion method, was based on a double contradiction that became standard for many centuries to come. This double contradiction is illustrated in figure 3, the accompanying diagram to the proposition.
Figure 3 Proposition XII.2 of Euclid’s Elements.
If the ratio of the square on BD to the square on FH is not the same as the ratio of circle ABCD to circle EFGH, then it must be the same as the ratio of circle ABCD to an area S either larger or smaller than circle EFGH. The curvilinear figures are approximated by polygons, since the continuity principle allows the difference between the inscribed polygon and the circle to be as close as desired (e.g., closer than the difference between S and EFGH). The “double contradiction” is reached if one assumes that S is either smaller or larger than EFGH.
Forms of proof and constructions other than those mentioned so far are occasionally found in Greek mathematical texts. These include diagrams based on what is assumed to be the synchronized motion of two lines (e.g., the trisectrix, or Archimedes’ spiral), mechanical devices of many sorts, or reasoning based on idealized mechanical considerations. However, the Euclidean type of proof described above remained a model to be followed wherever possible. There is a famous Archimedes palimpsest that provides evidence of how less canonical methods, drawing on mechanical considerations (albeit of a highly idealized kind), were used to deduce results about areas and volumes. However, even this bears testimony to the primacy of the ideal model: there is a letter from Archimedes to Eratosthenes in which he displays the ingenuity of his mechanical methods but at the same time is at pains to stress their heuristic character.
Just as Euclid is now considered to represent an entire mainstream tradition of Greek mathematics, so ALKHW RIZM
RIZM [VI.5] is regarded as a representative of Islamic mathematics. There are two main traits of his work that are relevant to the present account and that became increasingly central to the development of mathematics, starting with his works in the late eighth century and continuing until the works of CARDANO [VI.7] in sixteenth-century Italy. These traits are a pervasive “algebraization” of mathematical thinking, and a continued reliance on Euclidean-style geometric proof as the main way of legitimizing the validity of mathematical knowledge in general and of algebraic reasoning in mathematics in particular.
[VI.5] is regarded as a representative of Islamic mathematics. There are two main traits of his work that are relevant to the present account and that became increasingly central to the development of mathematics, starting with his works in the late eighth century and continuing until the works of CARDANO [VI.7] in sixteenth-century Italy. These traits are a pervasive “algebraization” of mathematical thinking, and a continued reliance on Euclidean-style geometric proof as the main way of legitimizing the validity of mathematical knowledge in general and of algebraic reasoning in mathematics in particular.
The prime example of this combination is found in al-Khw rizm
rizm ’s seminal text al-Kit
’s seminal text al-Kit b al-mukhta
b al-mukhta ar f
ar f
 is
is b al-jabr wa’l-muq
b al-jabr wa’l-muq bala (“The compendious book on calculation by completion and balancing”), where he discusses the solutions of problems in which the unknown length appears in combination with numbers and squares (the side of which is an unknown). Since he only envisages the possibility of positive “coefficients” and positive rational solutions, al-Khw
bala (“The compendious book on calculation by completion and balancing”), where he discusses the solutions of problems in which the unknown length appears in combination with numbers and squares (the side of which is an unknown). Since he only envisages the possibility of positive “coefficients” and positive rational solutions, al-Khw rizm
rizm needs to consider six different situations each of which requires a different recipe for finding the unknown: the full-grown idea of a general quadratic equation and an algorithm to solve it in all cases does not appear in Islamic mathematical texts. For instance, the problem “squares and roots equal to numbers” (e.g., x2 + 10x = 39, in modern notation) and the problem “roots and numbers equal to squares” (e.g., 3x + 4 = x2) are considered to be completely different ones, as are their solutions, and accordingly al-Khw
needs to consider six different situations each of which requires a different recipe for finding the unknown: the full-grown idea of a general quadratic equation and an algorithm to solve it in all cases does not appear in Islamic mathematical texts. For instance, the problem “squares and roots equal to numbers” (e.g., x2 + 10x = 39, in modern notation) and the problem “roots and numbers equal to squares” (e.g., 3x + 4 = x2) are considered to be completely different ones, as are their solutions, and accordingly al-Khw rizm
rizm treats them separately. In all cases, however, al-Khw
treats them separately. In all cases, however, al-Khw rizm
rizm proves the validity of the method described by translating it into geometric terms and then relying on Euclid-like geometric theorems built around a specific diagram. It is noteworthy, however, that the problems refer to specific numerical quantities associated with the magnitudes involved, and these measured magnitudes refer to the accompanying diagrams as well. In this way, al-Khw
proves the validity of the method described by translating it into geometric terms and then relying on Euclid-like geometric theorems built around a specific diagram. It is noteworthy, however, that the problems refer to specific numerical quantities associated with the magnitudes involved, and these measured magnitudes refer to the accompanying diagrams as well. In this way, al-Khw rizm
rizm interestingly departs from the Euclidean style of proof. Still, the Greek principle of homogeneity is essentially preserved, as the three quantities usually involved in the problem are all of the same kind, namely, areas.
interestingly departs from the Euclidean style of proof. Still, the Greek principle of homogeneity is essentially preserved, as the three quantities usually involved in the problem are all of the same kind, namely, areas.
Figure 4 Al-Khw rizm
rizm ’s geometric justification of the formula for a quadratic equation.
’s geometric justification of the formula for a quadratic equation.
Consider, for instance, the equation x2 + 10x = 39, which corresponds to the following problem of al-Khw rizm
rizm .
.
What is the square which combined with ten of its roots will give a sum total of 39?
The recipe prescribes the following steps.
Take one-half of the roots [5] and multiply them by itself [25]. Add this amount to 39 and obtain 64. Take the square root of this, which is eight, subtract from it half the roots, leaving three. The number three therefore represents one root of this square, which itself, of course, is nine.
The justification is provided by figure 4.
Here ab represents the said square, which for us is x2, and the rectangles c, d, e, f represent an area of 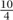 x each, so that all of them together equal 10x, as in the problem. Thus, the small squares in the corners represent an area of 6.25 each, and we can “complete” the large square, being equal to 64, and whose side is therefore 8, thus yielding the solution 3 for the unknown.
x each, so that all of them together equal 10x, as in the problem. Thus, the small squares in the corners represent an area of 6.25 each, and we can “complete” the large square, being equal to 64, and whose side is therefore 8, thus yielding the solution 3 for the unknown.
Abu Kamil Shuja, just one generation after al-Khw rizm
rizm , added force to this approach when he solved additional problems while specifically relying on theorems taken from the Elements, including the accompanying diagrams, in order to justify his method of solution. The primacy of the Euclidean-type proof, which was already accepted in geometry and arithmetic, thus also became associated with the algebraic methods that eventually turned into the main topic of interest in Renaissance mathematics. Cardano’s 1545 Ars Magna, the foremost example of this new trend, presented a complete treatment of the equations of third and fourth degree. Although the algebraic line of reasoning that he adopted and developed became increasingly abstract and formal, Cardano continued to justify his arguments and methods of solution by reference to Euclid-like geometric arguments based on diagrams.
, added force to this approach when he solved additional problems while specifically relying on theorems taken from the Elements, including the accompanying diagrams, in order to justify his method of solution. The primacy of the Euclidean-type proof, which was already accepted in geometry and arithmetic, thus also became associated with the algebraic methods that eventually turned into the main topic of interest in Renaissance mathematics. Cardano’s 1545 Ars Magna, the foremost example of this new trend, presented a complete treatment of the equations of third and fourth degree. Although the algebraic line of reasoning that he adopted and developed became increasingly abstract and formal, Cardano continued to justify his arguments and methods of solution by reference to Euclid-like geometric arguments based on diagrams.
The next significant change in the conception of proof appears in the seventeenth century. The most influential development of mathematics in this period was the creation of the infinitesimal calculus simultaneously by NEWTON [VI.14] and LEIBNIZ [VI.15]. This momentous development was the culmination of a process that spanned most of the century, involving the introduction and gradual improvement of important techniques for determining areas and volumes, gradients of tangents, and maxima and minima. These developments included the elaboration of traditional points of view that went back to the Greek classics, as well as the introduction of completely new ideas such as the “indivisibles,” whose status as a legitimate tool for mathematical proof was hotly debated. At the same time, the algebraic techniques and approaches that Renaissance mathematicians continued to expand upon, following on from their Islamic predecessors, now gained additional impetus and were gradually incorporated—starting with the work of FERMAT [VI.12] and DESCARTES [VI.11]—into the arsenal of tools available for proving geometric results. Underlying these various trends were different conceptions and practices of mathematical proof, which are briefly described and illustrated now.
Examples of how the classical Greek conception of geometric proof was essentially followed but at the same time fruitfully modified and expanded are found in the work of Fermat, as can be seen in his calculation of the area enclosed by a generalized hyperbola (in modern notation (y/a)m = (x/b)n (m, n ≠ 1)) and its asymptotes.
The quadratic hyperbola (i.e., a figure represented by y = 1/x2), for instance, is defined here in terms of a purely geometric relationship on any two of its points, namely, that the ratio between the squares built on the abscissas equals the inverse ratio between the lengths of the ordinates. In its original version it is expressed as follows: AG2 : AH2 :: IH : EG (see figure 5). It should be noticed that this is not an equation in the present sense of the word, on which the standard symbolic manipulations can be directly performed. Rather, this is a four-term proportion to which the rules of Greek classical mathematics apply. Also, the proof was entirely geometric and indeed it essentially followed the Euclidean style. Thus, if the segments AG, AH, AO, etc., are chosen in continued proportion, then one can prove that the rectangles EH, IO, NM, etc., are also in continued proportion, and indeed that EH : IO :: IO : NM :: … :: AH : AG.
Figure 5 Diagram for Fermat’s proof of the area under a hyperbola.
Fermat made use of proposition IX.35 of the Elements (mentioned above), which comprises an expression for the sum of any number of quantities in a geometric progression, namely (in more modern notation):
(an+1 - a1) : (a1 + a2 + ... + an) = (a2 - a1) : a1.
But at this point his proof takes an interesting turn. He introduces the somewhat obscure concept of “adequare,” which he found in the works of Diophantus, and which allows a kind of “approximate equality.” Specifically, this idea allows him to bypass the cumbersome procedure of double contradiction typically used in Greek geometry as an implicit passage to the infinite. A figure bounded by GE, by the horizontal asymptote, and by the hyperbola will equal the infinite sum of rectangles obtained when the rectangle EH “will vanish and will be reduced to nothing.” Further, proposition IX.35 implies that this sum equals the area of the rectangle BG. Significantly, Fermat still chose to rely on the authority of the ancients, hinting at the method of double contradiction when he declared that this result “would be easy to confirm by a more lengthy proof carried out in the manner of Archimedes.”
Attempts to expand the accepted canon of geometric proof eventually led to the more progressive approaches associated with the idea of indivisibles, as practiced by Cavalieri, Roberval, and Torricelli. This is well illustrated by Torricelli’s 1643 calculation of the volume of the infinite body created by rotating the hyperbola xy = k2 around the y-axis, with values of x between 0 and a (as we would describe it in modern terms).
The essential idea of indivisibles is that areas are considered to be sums, or collections, of infinitely many line segments, and volumes are considered to be sums, or collections, of infinitely many areas. In this example, Torricelli calculated the volume of revolution by considering it to be a sum of the curved surfaces of an infinite collection of cylinders successively inscribed within each other and having radii ranging from 0 to a. In modern algebraic terms, the height of the inscribed cylinder with radius x is k2/x, so the area of its curved surface is 2πx(k2/x) = π(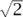 k)2, a constant value that is independent of x and equal to the area of a circle of radius
k)2, a constant value that is independent of x and equal to the area of a circle of radius 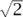 k. Thus, in Torricelli’s approach based on the geometry of indivisibles, the collection of all surfaces that, when taken together, comprise the infinite body can be equated to a collection of circles with area 2πk2, one for each x between 0 and a, or equivalently to a cylinder of volume 2πk2a.
k. Thus, in Torricelli’s approach based on the geometry of indivisibles, the collection of all surfaces that, when taken together, comprise the infinite body can be equated to a collection of circles with area 2πk2, one for each x between 0 and a, or equivalently to a cylinder of volume 2πk2a.
The rules of Euclid-like geometric proof were completely contravened in proofs of this kind and this made them unacceptable in the eyes of many. On the other hand, their fruitfulness was highly appealing, especially in cases like this one in which an infinite body was shown to have a finite volume, a result which Torricelli himself found extremely surprising. Both supporters and detractors alike, however, realized that techniques of this kind might lead to contradictions and inaccurate results. By the eighteenth century, with the accelerated development of the infinitesimal calculus and its associated techniques and concepts, techniques based on indivisibles had essentially disappeared.
The limits set by the classical paradigm of Euclidean geometric proof were then transgressed in a different direction by the all-embracing algebraization of geometry at the hands of Descartes. The fundamental step undertaken by Descartes was to introduce unit lengths as a key element in the diagrams used in geometric proofs. The radical innovation implied by this step, allowing the hitherto nonexistent possibility of defining operations with line segments, was explicitly stressed by Descartes in La Géométrie in 1637:
Just as arithmetic consists of only four or five operations, namely addition, subtraction, multiplication, division, and the extraction of roots, which may be considered a kind of division, so in geometry, to find required lines it is merely necessary to add or subtract other lines; or else, taking one line, which I shall call the unit in order to relate it as closely as possible to numbers, and which can in general be chosen arbitrarily, and having given two other lines, to find a fourth line which shall be to one of the given lines as the other is to the unit (which is the same as multiplication); or again, to find a fourth line which is to one of the given lines as the unit is to the other (which is equivalent to division); or, finally, to find one, two, or several mean proportionals between the unit and some other line (which is the same as extracting the square root, cube root, etc., of the given line).
Thus, for instance, given two segments BD, BE, the division of their lengths is represented by BC in figure 6, in which AB represents the unit length.
Although the proof was Euclid-like in appearance (because of the diagram and the use of the theory of similar triangles), the introduction of the unit length and its use for defining the operations with segments set it radically apart and opened completely new horizons for geometric proofs. Not only had measurements of length been absent from Euclidean-style proofs thus far, but also, as a consequence of the very existence of these operations, the essential dimensionality traditionally associated with geometric theorems lost its significance. Descartes used expressions such as a - b, a/b, a2, b3, and their roots, but he stressed that they should all be understood as “only simple lines, which, however, I name squares, cubes, etc., so that I make use of the terms employed in algebra.” With the removal of dimensionality, the requirement of homogeneity also became unnecessary. Unlike his predecessors, who handled magnitudes only when they had a direct geometric significance, Descartes could not see any problem in forming an expression such as a2b2 - b and then extracting its cube root. In order to do so, he said “we must consider the quantity a2b2 divided once by the unit, and the quantity b multiplied twice by the unit.” Sentences of this kind would be simply incomprehensible to Greek geometers, as well as to their Islamic and Renaissance followers.
This algebraization of geometry, and particularly the newly created possibility of proving geometric facts via algebraic procedures, was strongly related to the recent consolidation of the idea of an algebraic equation, seen as an autonomous mathematical entity, for which formal rules of manipulation were well-known and could be systematically applied. This idea reached full maturity in the hands of VIÈTE [VI.9] only around 1591. But not all mathematicians in the seventeenth century saw the important developments associated with algebraic thinking either as a direction to be naturally adopted or as a clear sign of progress in the latter discipline. A prominent opponent of any attempt to deviate from the classical Euclidean-style approach in geometry was none other than NEWTON [VI.14], who, in the Arithmetica Universalis (1707), was emphatic in expressing his views:
Figure 6 Descartes’s geometric calculation of the division of two given segments.
Equations are expressions of arithmetic computation and properly have no place in geometry, except in so far as truly geometrical quantities (lines, surfaces, solids and proportions) are thereby shown equal, some to others. Multiplications, divisions, and computations of that kind have recently been introduced into geometry, unadvisedly and against the first principle of this science. . . . Therefore these two sciences ought not to be confounded, and recent generations by confounding them have lost that simplicity in which all geometrical elegance consists.
Newton’s Principia bears witness to the fact that statements like this one were far from mere lip service, as Newton consistently preferred Euclidean-style proofs, considering them to be the correct language for presenting his new physics and for bestowing it with the highest degree of certainty. He used his own calculus only where strictly necessary, and barred algebra from his treatise entirely.
Mathematical analysis became the primary focus of mathematicians in the eighteenth century. Questions relating to the foundations of analysis arose immediately after the calculus began to be developed and were not settled until the late nineteenth century. To a considerable extent these questions were about the nature of legitimate mathematical proof, and debates about them played an important role in undermining the long-undisputed status of geometry as the basis for mathematical certainty and bestowing this status on arithmetic instead. The first important stage in this process was EULER’s [VI.19] reformulation of the calculus. Once separated from its purely geometric roots, the calculus came to be centered on the algebraically oriented concept of function. This trend for favoring algebra over geometry was given further impetus by Euler’s successors. D’ALEMBERT [VI.20], for instance, associated mathematical certainty above all with algebra—because of its higher degree of generality and abstraction—and only subsequently with geometry and mechanics. This was a clear departure from the typical views of Newton and of his contemporaries. The trend reached a peak and was transformed into a well-conceived program in the hands of LAGRANGE [VI.22], who in the preface to his 1788 Méchanique Analitique famously expressed a radical view about how one could achieve certainty in the mathematical sciences while distancing oneself from geometry. He wrote as follows:
One will not find figures in this work. The methods that I expound require neither constructions, nor geometrical or mechanical arguments, but only algebraic operations, subject to a regular and uniform course.
The details of these developments are beyond the scope of this article. What is important to stress, however, is that in spite of their very considerable impact, the basic conceptions of proof in the more mainstream realm of geometry did not change very much during the eighteenth century. An illuminating perspective on these conceptions is offered by the views of contemporary philosophers, especially Immanuel Kant.
Kant had a very profound knowledge of contemporary science, and particularly of mathematics. A philosophical discussion of his views on mathematical knowledge and proof need not concern us here. However, given his acquaintance with contemporary conceptions, they do provide an insightful historical perspective on proof as it was understood at the time. Of particular interest is the contrast he draws between a philosophical argument, on the one hand, and a geometric proof, on the other. Whereas the former deals with general concepts, the latter deals with concrete, yet nonempirical, concepts, by reference to “visualizable intuitions” (Anschauung). This difference is epitomized in the following, famous passage from his Critique of Pure Reason.
Suppose a philosopher be given the concept of a triangle and he is left to find out, in his own way, what relation the sum of its angles bears to a right angle. He has nothing but the concept of a figure enclosed by three straight lines, and possessing three angles. However long he meditates on this concept, he will never produce anything new. He can analyze and clarify the concept of a straight line or of an angle or of the number three, but he can never arrive at any properties not already contained in these concepts. Now let the geometrician take up these questions. He at once begins by constructing a triangle. Since he knows that the sum of two right angles is exactly equal to the sum of all the adjacent angles which can be constructed from a single point on a straight line, he prolongs one side of his triangle and obtains two adjacent angles, which together are equal to two right angles. He then divides the external angle by drawing a line parallel to the opposite side of the triangle, and observes that he has thus obtained an external adjacent angle which is equal to an internal angle—and so on. In this fashion, through a chain of inferences guided throughout by intuition, he arrives at a fully evident and universally valid solution of the problem.
In a nutshell, then, for Kant the nature of mathematical proof that sets it apart from other kinds of deductive argumentation (like philosophy) lies in the centrality of the diagrams and the role that they play. As in the Elements, this diagram is not just a heuristic guide for what is no more than abstract reasoning, but rather an “intuition,” a singular embodiment of the mathematical idea that is clearly located not only in space, but rather in space and time. In fact,
I cannot represent to myself a line, however small, without drawing it in thought, that is gradually generating all its parts from a point. Only in this way can the intuition be obtained.
This role played by diagrams as “visualizable intuitions” is what provides, for Kant, the explanation of why geometry is not just an empirical science, but also not just a huge tautology devoid of any synthetic content. According to him, geometric proof is constrained by logic but it is much more than just a purely logical analysis of the terms involved. This view was at the heart of a novel philosophical analysis whose starting point was the then-entrenched conception of what a mathematical proof is.
The nineteenth century was full of important developments in geometry and other parts of mathematics, not just of the methods but also of the aims of the various subdisciplines. Logic, as a field of knowledge, also underwent significant changes and a gradual mathematization that entirely transformed its scope and methods. Consequently, by the end of the century the conception of proof and its role in mathematics had also been deeply transformed.
In Göttingen in 1854 RIEMANN [VI.49] gave his seminal talk “On the hypotheses which lie at the foundations of geometry.” At around the same time, the works of BOLYAI [VI.34] and LOBACHEVSKII [VI.31] on non-Euclidean geometry, as well as the related ideas of GAUSS [VI.26], all dating from the 1830s, began to be more generally known. The existence of coherent, alternative geometries brought about a pressing need for the most basic, longstanding beliefs about the essence of geometric knowledge, including the role of proof and mathematical rigor, to be revised. Of even greater significance in this regard was the renewed interest in PROJECTIVE GEOMETRY [I.3 §6.7], which became a very active field of research with its own open research questions and foundational issues after the publication of Jean Poncelet’s 1822 treatise. The addition of projective geometry to the many other possible geometric perspectives prompted a variety of attempts at unification and classification, the most significant of which were those based on group-theoretic ideas. Particularly notable were those of KLEIN [VI.57] and LIE [VI.53] in the 1870s. In 1882, Moritz Pasch published an influential treatise on projective geometry devoted to a systematic exploration of its axiomatic foundations and the interrelationships among its fundamental theorems. Pasch’s book also attempted to close the many logical gaps that had been found in Euclidean geometry over the years. More systematically than any of his fellow nineteenth-century mathematicians, Pasch emphasized that all geometric results should be obtained from axioms by strict logical deduction, without relying on analytical means, and above all without appeal to diagrams or to properties of the figures involved. Thus, although in some ways he was consciously reverting to the canons of Euclid-like proof (which by then were somewhat loosened), his attitude toward diagrams was fundamentally different. Aware of the potential limitations of visualizing diagrams (and perhaps their misleading influence) he put a much greater emphasis on the pure logical structure of the proof than his predecessors had. Nevertheless, he was not led to an outright formalist view of geometry and geometric proof. Rather, he consistently adopted an empirical approach to the origins and meaning of geometry and fell short of claiming that diagrams were for heuristic use only:
The basic propositions [of geometry] cannot be understood without corresponding drawings; they express what has been observed from certain, very simple facts. The theorems are not founded on observations, but rather, they are proved. Every inference performed during a deduction must find confirmation in a drawing, yet it is not justified by a drawing but from a certain preceding statement (or a definition).
Pasch’s work definitely contributed to diagrams losing their central status in geometric proofs in favor of purely deductive relations, but it did not directly lead to a thorough revision of the status of the axioms of geometry, or to a change in the conception that geometry deals essentially with the study of our spatial, visualizable intuition (in the sense of Anschauung). The all-important nineteenth-century developments in geometry produced significant changes in the conception of proof only under the combined influence of additional factors.
Mathematical analysis continued to be a primary field of research, and the study of its foundations became increasingly identified with arithmetic, rather than geometric, rigor. This shift was provoked by the works of mathematicians like CAUCHY [VI.29], WEIERSTRASS [VI.44], CANTOR [VI.54], and DEDEKIND [VI.50], which aimed at eliminating intuitive arguments and concepts in favor of ever more elementary statements and definitions. (In fact, it was not until the work of Dedekind on the foundations of arithmetic, in the last third of the century, that the rigorous formulation pursued in these works was given any kind of axiomatic underpinning.) The idea of investigating the axiomatic basis of mathematical theories, whether geometry, algebra, or arithmetic, and of exploring alternative possible systems of postulates was indeed pursued during the nineteenth century by mathematicians such as George Peacock, Charles Babbage, John Herschel, and, in a different geographical and mathematical context, Hermann Grassmann. But such investigations were the exception rather than the rule, and they had only a fairly limited role in shaping a new conception of proof in analysis and geometry.
One major turning point, where the above trends combined to produce a new kind of approach to proof, is to be found in the works of GIUSEPPE PEANO [VI.62] and his Italian followers. Peano’s mainstream activities were as a competent analyst, but he was also interested in artificial languages, and particularly in developing an artificial language that would allow a completely formal treatment of mathematical proofs. In 1889 his successful application of such a conceptual language to arithmetic yielded his famous POSTULATES FOR THE NATURAL NUMBERS [III.67]. Pasch’s systems of axioms for projective geometry posed a challenge to Peano’s artificial language, and he set out to investigate the relationship between the logical and the geometric terms involved in the deductive structure of geometry. In this context he introduced the idea of an independent set of axioms, and applied this concept to his own system of axioms for projective geometry, which were a slight modification of Pasch’s. This view did not lead Peano to a formalistic conception of proof, and he still conceived geometry in terms very similar to his predecessors:
Anyone is allowed to take a hypothesis and develop its logical consequences. However, if one wants to give this work the name of geometry it is necessary that such hypotheses or postulates express the result of simple and elementary observations of physical figures.
Under the influence of Peano, Mario Pieri developed a symbolism with which to handle abstract–formal theories. Unlike Peano and Pasch, Pieri consistently promoted the idea of geometry as a purely logical system, where theorems are deduced from hypothetical premises and where the basic terms are completely detached from any empirical or intuitive significance.
A new chapter in the history of geometry and of proof was opened at the end of the nineteenth century with the publication of HILBERT’s [VI.63] Grundlagen der Geometrie, a work that synthesized and brought to completion the various trends of geometric research described above. Hilbert was able to achieve a comprehensive analysis of the logical interrelations among the fundamental results of projective geometry, such as the theorems of Desargues and Pappus, while paying particular attention to the role of continuity considerations within their proofs. His analysis was based on the introduction of a generalized analytic geometry, in which the coordinates may be taken from a variety of different NUMBER FIELDS [III.63], rather than from the real numbers alone. This approach created a purely synthetic arithmetization of any given type of geometry, and thus helped to clarify the logical structure of Euclidean geometry as a deductive system. It also clarified the relationship between Euclidean geometry and the various other kinds of known geometries—non-Euclidean, projective, or non-Archimedean. This focus on logic implied, among other things, that diagrams should be relegated to a merely heuristic role. In fact, although diagrams still appear in many proofs in the Grundlagen, the entire purpose of the logical analysis is to avoid being misled by diagrams. Proofs, and particularly geometric proofs, have thus become purely logical arguments, rather than arguments about diagrams. And at the same time, the essence and the role of the axioms from which the derivations in question start also underwent a dramatic change.
Following Pasch’s lead, Hilbert introduced a new system of axioms for geometry that attempted to close the logical gaps inherent in earlier systems. These axioms were of five kinds—axioms of incidence, of order, of congruence, of parallels, and of continuity—each of which expressed a particular way in which spatial intuition manifests itself in our understanding. They were formulated for three fundamental kinds of object: points, lines, and planes. These remained undefined, and the system of axioms was meant to provide an implicit definition of them. In other words, rather than defining points or lines at the outset and then postulating axioms that are assumed to be valid for them, a point and a line were not directly defined, except as entities that satisfy the axioms postulated by the system. Further, Hilbert demanded that the axioms in a system of this kind should be mutually independent, and introduced a method for checking that this demand is fulfilled; in order to do so, he constructed models of geometries that fail to satisfy a given axiom of the system but satisfy all the others. Hilbert also required that the system be consistent, and that the consistency of geometry could be made to depend, in his system, on that of arithmetic. He initially assumed that proving the consistency of arithmetic would not present a major obstacle and it was a long time before he realized that this was not the case. Two additional requirements that Hilbert initially introduced for axiomatic systems were simplicity and completeness. Simplicity meant, in essence, that an axiom should not contain more than “a single idea.” The demand that every axiom in a system be “simple,” however, was never clearly defined or systematically pursued in subsequent works of Hilbert or any of his successors. The last requirement, completeness, meant for Hilbert in 1900 that any adequate axiomatization of a mathematical domain should allow for a derivation of all the known theorems of the discipline in question. Hilbert claimed that his axioms would indeed yield all the known results of Euclidean geometry, but of course this was not a property that he could formally prove. In fact, since this property of “completeness” cannot be formally checked for any given axiomatic system, it did not become one of the standard requirements of an axiomatic system. It is important to note that the concept of completeness used by Hilbert in 1900 is completely different from the currently accepted, model-theoretical one that appeared much later. The latter amounts to the requirement that in a given axiomatic system every true statement, be it known or unknown, should be provable.
The use of undefined concepts and the concomitant conception of axioms as implicit definitions gave enormous impetus to the view of geometry as a purely logical system, such as Pieri had devised it, and eventually transformed the very idea of truth and proof in mathematics. Hilbert claimed on various occasions—echoing an idea of Dedekind—that, in his system, “points, lines, and planes” could be substituted by “chairs, tables, and beer mugs,” without thereby affecting in any sense the logical structure of the theory. Moreover, in the light of discussions about set-theoretical paradoxes, Hilbert strongly emphasized the view that the logical consistency of a concept implicitly defined by axioms was the essence of mathematical existence. Under the influence of these views, of the new methodological tools introduced by Hilbert, and of the successful overview of the foundations of geometry thus achieved, many mathematicians went on to promote new views of mathematics and new mathematical activities that in many senses went beyond the views embodied in Hilbert’s approach. On the one hand, a trend that thrived in the United States at the beginning of the twentieth century, led by Eliakim H. Moore, turned the study of systems of postulates into a mathematical field in its own right, independent of direct interest in the field of research defined by the systems in question. For instance, these mathematicians defined the minimal set of independent postulates for groups, fields, projective geometry, etc., without then proceeding to investigate of any of these individual disciplines. On the other hand, prominent mathematicians started to adopt and develop increasingly formalistic views of proof and of mathematical truth, and began applying them in a growing number of mathematical fields. The work of the radically modernist mathematician FELIX HAUSDORFF [VI.68] provides important examples of this trend, as he was among the first to consistently associate Hilbert’s achievement with a new, formalistic view of geometry. In 1904, for instance, he wrote:
In all philosophical debates since Kant, mathematics, or at least geometry, has always been treated as heteronomous, as dependent on some external instance of what we could call, for want of a better term, intuition, be it pure or empirical, subjective or scientifically amended, innate or acquired. The most important and fundamental task of modern mathematics has been to set itself free from this dependency, to fight its way through from heteronomy to autonomy.
Hilbert himself would pursue such a point of view around 1918, when he engaged in the debates about the consistency of arithmetic and formulated his “finitist” program. This program did indeed adopt a strongly formalistic view, but it did so with the restricted aim of solving this particular problem. It is therefore important to stress that Hilbert’s conceptions of geometry were, and remained, essentially empiricist and that he never regarded his axiomatic analysis of geometry as part of an overall formalistic conception of mathematics. He considered the axiomatic approach as a tool for the conceptual clarification of existing, well-elaborated theories, of which geometry provided only the most prominent example.
The implication of Hilbert’s axiomatic approach for the concept of proof and of truth in mathematics provoked strong reactions from some mathematicians, and prominently so from FREGE [VI.56]. Frege’s views are closely related to the changing status of logic at the turn of the twentieth century and its gradual process of mathematization and formalization. This process was an outcome of the successive efforts through the nineteenth century of BOOLE [VI.43], DE MORGAN [VI.38], Grassmann, Charles S. Peirce, and Ernst Schröder at formulating an algebra of logic. The most significant step toward a new, formal conception of logic, however, came with the increased understanding of the role of the logical QUANTIFIERS [I.2 §3.2] (universal, ∀, and existential, ∃) in the process of formulating a modern mathematical proof. This understanding emerged in an informal, but increasingly clear, fashion as part of the process of the rigorization of analysis and the distancing from visual intuition, especially at the hands of Cauchy, BOLZANO [VI.28], and Weierstrass. It was formally defined and systematically codified for the first time by Frege in his 1879 Begriffsschrift. Frege’s system, as well as similar ones proposed later by Peano and by RUSSELL [VI.71], brought to the fore a clear distinction between propositional connectives and quantifiers, as well as between logical symbols and algebraic or arithmetic ones.
Frege formulated the idea of a formal system , in which one defines in advance all the allowable symbols, all the rules that produce well-formed formulas, all axioms (i.e., certain preselected, well-formed formulas), and all the rules of inference. In such systems any deduction can be checked syntactically —in other words, by purely symbolic means. On the basis of such systems Frege aimed to produce theories with no logical gaps in their proofs. This would apply not only to analysis and to its arithmetic foundation—the mathematical fields that provided the original motivation for his work—but also to the new systems of geometry that were evolving at the time. On the other hand, in Frege’s view the axioms of mathematical theories—even if they appear in the formal system merely as well-formed formulas—embody truths about the world. This is precisely the source of his criticism of Hilbert. It is the truth of the axioms, asserted Frege, that certifies their consistency, rather than the other way around, as Hilbert suggested.
We thus see how foundational research in two separate fields—geometry and analysis—was inspired by different methodologies and philosophical outlooks, but converged at the turn of the twentieth century to create an entirely new conception of mathematical proof. In this conception a mathematical proof is seen as a purely logical construct validated in purely syntactic terms, independently of any visualization through diagrams. This conception has dominated mathematics ever since.
The new notion of proof that stabilized at the beginning of the twentieth century provided an idealized model—broadly accepted to this day—of what should constitute a valid mathematical argument. To be sure, actual proofs devised and published by mathematicians since that time are seldom presented as fully formalized texts. They typically present a clearly articulated argument in a language that is precise enough to convince the reader that it could—in principle, and perhaps with straightforward (if sustained) effort—be turned into one. Throughout the decades, however, some limitations of this dominant idea have gradually emerged and alternative conceptions of what should count as a valid mathematical argument have become increasingly accepted as part of current mathematical practice.
The attempt to pursue this idea systematically to its full extent led, early on and very unexpectedly, to a serious difficulty with the notion of a proof as a completely formalized and purely syntactic deductive argument. In the early 1920s, Hilbert and his collaborators developed a fully fledged mathematical theory whose subject matter was “proof,” considered as an object of study in itself. This theory, which presupposed the formal conception of proof, arose as part of an ambitious program for providing a direct, finitistic consistency proof of arithmetic represented as a formalized system. Hilbert asserted that, just as the physicist examines the physical apparatus with which he carries out his experiments and the philosopher engages in a critique of reason, so the mathematician should be able to analyze mathematical proofs and do so strictly by mathematical means. About a decade after the program was launched, GÖDEL [VI.92] came up with his astonishing INCOMPLETENESS THEOREM [V.15], which famously showed that “mathematical truth” and “provability” were not one and the same thing. Indeed, in any consistent, sufficiently rich axiomatic system (including the systems typically used by mathematicians) there are true mathematical statements that cannot be proved. Gödel’s work implied that Hilbert’s finitistic program was too optimistic, but at the same time it also made clear the deep mathematical insights that could be obtained from Hilbert’s proof theory.
A closely related development was the emergence of proofs that certain important mathematical statements were undecidable. Interestingly, these seemingly negative results have given rise to new ideas about the legitimate grounds for establishing the truth of such statements. For instance, in 1963 Paul Cohen established that the CONTINUUM HYPOTHESIS [IV.22 §5] can be neither proved nor disproved in the usual systems of axioms for set theory. Most mathematicians simply accept this idea and regard the problem as solved (even if not in the way that was originally expected), but some contemporary set theorists, notably Hugh Woodin, maintain that there are good reasons to believe that the hypothesis is false. The strategy they follow in order to justify this assertion is fundamentally different from the formal notion of proof: they devise new axioms, demonstrate that these axioms have very desirable properties, argue that they should therefore be accepted, and then show that they imply the negation of the continuum hypothesis. (See SET THEORY [IV.22 §10] for further discussion.)
A second important challenge came from the ever-increasing length of significant proofs appearing in various mathematical domains. A prominent example was the CLASSIFICATION THEOREM FOR FINITE SIMPLE GROUPS [V.7], whose proof was worked out in many separate parts by a large numbers of mathematicians. The resulting arguments, if put together, would reach about ten thousand pages, and errors have been found since the announcement in the early 1980s that the proof was complete. It has always been relatively straightforward to fix the errors and the theorem is indeed accepted and used by group theorists. Nevertheless, the notion of a proof that is too long for a single human being to check is a challenge to our conception of when a proof should be accepted as such. The more recent, very conspicuous cases of FERMAT’S LAST THEOREM [V.10] and THE POINCARÉ CONJECTURE [V.25] were hard to survey for different reasons: not only were they long (though nowhere near as long as the classification of finite simple groups), but they were also very difficult. In both cases there was a significant interval between the first announcement of the proofs and their complete acceptance by the mathematical community because checking them required enormous efforts by the very few people qualified to do so. There is no controversy about either of these two breakthroughs, but they do raise an interesting sociological problem: if somebody claims to have proved a theorem and nobody else is prepared to check it carefully (perhaps because, unlike the two theorems just mentioned, this one is not important enough for another mathematician to be prepared to spend the time that it would take), then what is the status of the theorem?
Proofs based on probabilistic considerations have also appeared in various mathematical domains, including number theory, group theory, and combinatorics. It is sometimes possible to prove mathematical statements (see, for example, the discussion of random primality testing in COMPUTATIONAL NUMBER THEORY [IV.3 §2]), not with complete certainty, but in such a way that the probability of error is tiny—at most one in a trillion, say. In such cases, we may not have a formal proof, but the chances that we are mistaken in considering the given statement to be true are probably lower than, say, the chance that there is a significant mistake in one of the lengthy proofs mentioned above.
Another challenge has come from the introduction of computer-assisted methods of proof. For instance, in 1976 Kenneth Appel and Wolfgang Haken settled a famous old problem by proving the FOUR-COLOR THEOREM [V.12]. Their proof involved the checking of a huge number of different map configurations, which they did with the help of a computer. Initially, this raised debates about the legitimacy of their proof but it quickly became accepted and there are now several proofs of this kind. Some mathematicians even believe that computer-assisted and, more importantly, computer-generated proofs are the future of the entire discipline. Under this (currently minority) view, our present views about what counts as an acceptable mathematical proof will soon become obsolete.
A last point to stress is that many branches of mathematics now contain conjectures that seem to be both fundamentally important and out of reach for the foreseeable future. Mathematicians persuaded of the truth of such conjectures increasingly undertake the systematic study of their consequences, assuming that an acceptable proof will one day appear (or at least that the conjecture is true). Such conditional results are published in leading mathematical journals and doctoral degrees are routinely awarded for them.
These trends all raise interesting questions about existing conceptions of legitimate mathematical proofs, the status of truth in mathematics, and the relationship between “pure” and “applied” fields. The formal notion of a proof as a string of symbols that obeys certain syntactical rules continues to provide an ideal model for the principles that underlie what most mathematicians see as the essence of their discipline. It allows far-reaching mathematical analysis of the power of certain axiomatic systems, but at the same time it falls short of explaining the changing ways in which mathematicians decide what kinds of arguments they are willing to accept as legitimate in their actual professional practice.
Acknowledgments. I thank José Ferreirós and Reviel Netz for useful comments on previous versions of this text.
Bos, H. 2001.Redefining Geometrical Exactness. Descartes’ Transformation of the Early Modern Concept of Construction. New York: Springer.
Ferreirós, J. 2000. Labyrinth of Thought. A History of Set Theory and Its Role in Modern Mathematics. Boston, MA: Birkhäuser.
Grattan-Guinness, I. 2000. The Search for Mathematical Roots, 1870–1940: Logics, Set Theories and the Foundations of Mathematics from Cantor through Russell to Gödel. Princeton, NJ: Princeton University Press.
Netz, R. 1999. The Shaping of Deduction in Greek Mathematics: A Study in Cognitive History. Cambridge: Cambridge University Press.
Rashed, R. 1994. The Development of Arabic Mathematics: Between Arithmetic and Algebra, translated by A. F. W. Armstrong. Dordrecht: Kluwer.