III.3 Bayesian Analysis
Suppose you throw a pair of standard dice. The probability that the total is 10 is 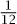 because there are thirty-six ways the dice can come up, of which three (4 and 6, 5 and 5, and 6 and 4) give 10. If, however, you look at the first die and see that it came up as a 6, then the conditional probability that the total is 10, given this information, is
because there are thirty-six ways the dice can come up, of which three (4 and 6, 5 and 5, and 6 and 4) give 10. If, however, you look at the first die and see that it came up as a 6, then the conditional probability that the total is 10, given this information, is 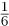 (since that is the probability that the other die comes up as a 4).
(since that is the probability that the other die comes up as a 4).
In general, the probability of A given B is defined to be the probability of A and B divided by the probability of B. In symbols, one writes
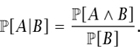
From this it follows that  [A ∧ B] =
[A ∧ B] =  [A|B]
[A|B]  [B]. Now
[B]. Now  [A ∧ B] is the same as
[A ∧ B] is the same as  [B ∧ B]. Therefore,
[B ∧ B]. Therefore,
 [A|B]
[A|B]  [B] =
[B] =  [B|A]
[B|A]  [A],
[A],
since the left-hand side is  [A ∧ B] and the right-hand side is
[A ∧ B] and the right-hand side is  [B ∧ A]. Dividing through by
[B ∧ A]. Dividing through by  [B] we obtain Bayes’s theorem:
[B] we obtain Bayes’s theorem:
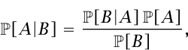
which expresses the conditional probability of A given B in terms of the conditional probability of B given A.
A fundamental problem in statistics is to analyze random data given by an unknown PROBABILITY DISTRIBUTION [III.71]. Here, Bayes’s theorem can make a significant contribution. For example, suppose you are told that some unbiased coins have been tossed and that three of them have come up heads. Suppose that you are told that the number of coins tossed is between 1 and 10, and that you wish to guess this number. Let H3 stand for the event that three coins came up heads and let C be the number of coins. Then for each n between 1 and 10 it is not hard to calculate the conditional probability  [H3| C = n], but we would like to know the reverse, namely
[H3| C = n], but we would like to know the reverse, namely  [C = n|H3]. Bayes’s theorem tells us that it is
[C = n|H3]. Bayes’s theorem tells us that it is
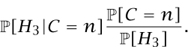
This would tell us the ratios between the various conditional probabilities  [C = n| H3] if we knew what the probabilities
[C = n| H3] if we knew what the probabilities  [C = n] were. Typically, one does not know this, but one makes some kind of guess, called a prior distribution. For example, one might guess, before knowing that three coins had come up heads, that for each n between 1 and 10 the probability that n coins had been chosen was
[C = n] were. Typically, one does not know this, but one makes some kind of guess, called a prior distribution. For example, one might guess, before knowing that three coins had come up heads, that for each n between 1 and 10 the probability that n coins had been chosen was 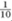 . After this information, one would use the calculation above to revise one’s assessment and obtain a posterior distribution, in which the probability that C = n would be proportional to
. After this information, one would use the calculation above to revise one’s assessment and obtain a posterior distribution, in which the probability that C = n would be proportional to 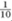
 [H3|C = n].
[H3|C = n].
There is more to Bayesian analysis than simply applying Bayes’s theorem to replace prior distributions by posterior distributions. In particular, as in the example just given, there is not always an obvious prior distribution to take, and it is a subtle and interesting mathematical problem to devise methods for choosing prior distributions that are “optimal” in different ways. For further discussion, see MATHEMATICS AND MEDICAL STATISTICS [VII.11] and MATHEMATICAL STATISTICS [VII.10].
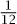 because there are thirty-six ways the dice can come up, of which three (4 and 6, 5 and 5, and 6 and 4) give 10. If, however, you look at the first die and see that it came up as a 6, then the conditional probability that the total is 10, given this information, is
because there are thirty-six ways the dice can come up, of which three (4 and 6, 5 and 5, and 6 and 4) give 10. If, however, you look at the first die and see that it came up as a 6, then the conditional probability that the total is 10, given this information, is 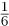 (since that is the probability that the other die comes up as a 4).
(since that is the probability that the other die comes up as a 4).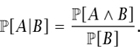
 [A ∧ B] =
[A ∧ B] = 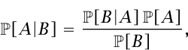
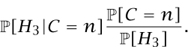
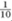 . After this information, one would use the calculation above to revise one’s assessment and obtain a posterior distribution, in which the probability that C = n would be proportional to
. After this information, one would use the calculation above to revise one’s assessment and obtain a posterior distribution, in which the probability that C = n would be proportional to