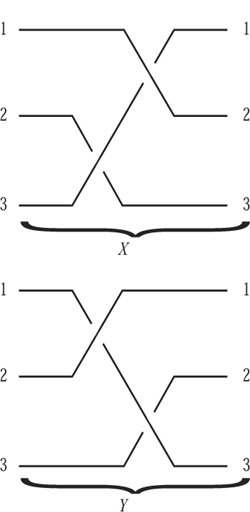
Take two parallel planes, each punctured at n points. Label the holes 1 to n in each plane, and run a string from each hole in the first plane to one in the second, in such a way that no two strings go to the same hole. The result is an n-braid. Two different 3-braids, shown in two-dimensional projection in a similar manner to KNOT DIAGRAMS [III.44], are given in figure 1.
As the diagrams suggest, we insist that the strings go from left to right without “doubling back”; so, for example, a knotted string is not allowed.
A certain freedom is allowed when we describe a braid: provided that the string ends remain fixed and the strings do not break or pass through each other, one can stretch, contract, bend, and otherwise move the strings about in three dimensions and end up with the “same” braid. This notion of “sameness” is an EQUIVALENCE RELATION [I.2 §2.3] called braid isotopy.
Braids may be composed as follows: arrange a pair of braids end to end to abut in a common (middle) plane, join up the strings, and remove the middle plane. For the braids X and Y in figure 1, the composition XY is given in figure 2.

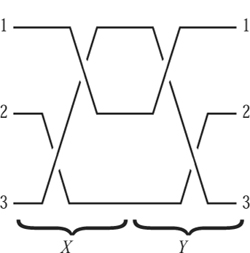
With this notion of composition, n-braids form a group Bn. In our example, Y = X-1, since “pulling all the strings tight” shows that XY is isotopic to the trivial braid (figure 3), which acts as the identity.

As a group, Bn is generated by elements (σi)1 ≤ i≤ n-1, where σi is formed from the trivial braid by crossing the ith string over the (i + 1)st as in figure 4. The reader may perceive a similarity between the σi and the adjacent transpositions that generate the group Sn of PERMUTATIONS [III.68] of {1, . . . , n}. Indeed, any braid determines a permutation by the rule
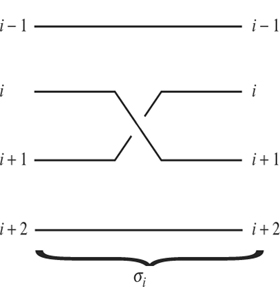
i ↦ right-hand label of i th string.
Ignoring everything except the behavior at the ends gives a surjective homomorphism Bn → Sn, which maps σi to the transposition (i, i + 1). This is not an isomorphism, however, as Bn is infinite In fact, σi has infinite order, whereas the transposition (i, i + 1) squares to the identity. In his celebrated 1925 paper “Theorie der Zöpfe,” ARTIN [VI.86] showed that multiplication in Bn is completely described by the relations
σiσj = σjσi (|i-j| ≥ 2),
σi σi+1 σi = σi+1σiσi+1.
These relations have subsequently acquired importance in statistical physics, where they are known as the Yang–Baxter equations.
In groups defined by generators and relations it is usually difficult (there being no method that works uniformly in all cases) to decide whether an arbitrary word in the generators represents the identity element (see GEOMETRIC AND COMBINATORIAL GROUP THEORY [IV.10]). For Bn, Artin solved this problem geometrically, by “combing the braid.” An alternative algebraic method, due to Garside (1967), also decides when two elements in Bn are conjugate.
In relation to the decidability of such questions, and in many other respects, braid groups display close affinities with linear groups: that is, groups in which all elements behave as if they were invertible N × N matrices. Although such similarities suggested that it should be possible to prove that braid groups genuinely are linear, the problem of doing so remained unsolved for many years, until in 2001 a proof was eventually found by Bigelow and independently by Krammer.
The groups described here are, strictly speaking, braid groups of the plane, the plane being the object punctured. Other braid groups also occur, often in surprising contexts. The connection with statistical physics has already been mentioned. They also arise in algebraic geometry, when algebraic curves become punctured by discarding exceptional points. Thus, though originating in topology, braids may intervene significantly in areas such as “constructive Galois theory” that seem at first sight to be purely algebraic.