 should not also appear as
should not also appear as 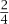 or
or 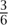 ). This leads to an ordering such as 0, 1, -1,2, -2,
). This leads to an ordering such as 0, 1, -1,2, -2,  , -
, -  , 3, -3,
, 3, -3, 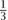 , -
, -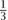 ,
, 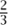 , -
, - 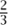 ,
, 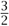 , -
, - 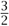 , 4, -4, . . . .
, 4, -4, . . . .Infinite sets arise all the time in mathematics: the natural numbers, the squares, the primes, the integers, the rationals, the reals, and so on. It is often natural to try to compare the sizes of these sets: intuitively, one feels that the set of natural numbers is “smaller” than the set of integers (as it contains just the positive ones), and much larger than the set of squares (since a typical large integer is unlikely to be a square). But can we make comparisons of size in a precise way?
An obvious method of attack is to build on our intuition about finite sets. If A and B are finite sets, there are two ways we might go about comparing their sizes. One is to count their elements: we obtain two nonnegative integers m and n and just look at whether m < n, m = n, or m > n. But there is another important method, which does not require us to know the sizes of either A or B. This is to pair off elements from A with elements of B until one or other of the sets runs out of elements: the first one to run out is the smaller set, and if there is a dead heat, then the sets have the same size.
A suitable modification of this second method works for infinite sets as well: we can declare two sets to be of equal size if there is a one-to-one correspondence between them. This turns out to be an important and useful definition, though it does have some consequences that seem a little odd at first. For example, there is an obvious one-to-one correspondence between natural numbers and perfect squares: for each n we let n correspond to n2. Thus, according to this definition there are “as many” squares as there are natural numbers. Similarly, we could show that there are as many primes as natural numbers by associating n with the nth prime number.1
What about ℤ? It seems that it should be “twice as large” as ℕ, but again we can find a one-to-one correspondence between them. We just list the integers in the order 0, 1, -1, 2, -2, 3, -3, . . and then match the natural numbers with them in the obvious way: 1 with 0, then 2 with 1, then 3 with -1, then 4 with 2, then 5 with -2, and so on.
An infinite set is called countable if it has the same size as the natural numbers. As the above example shows, this is exactly the same as saying that we can list the elements of the set. Indeed, if we have listed a set as a1, a2, a3, . . . , then our correspondence is just to send n to an. It is worth noting that there are of course many attempted listings that fail: for example, for ℤ we might have tried -3, -2, -1, 0, 1, 2, 3, 4, . . . . So it is important to recognize that when we say that a set is countable we are not saying that every attempt to list it works, or even that the obvious attempt does: we are merely saying that there is some way of listing the elements. This is in complete contrast to finite sets, where if we attempt to match up two sets and find some elements of one set left over, then we know that the two sets cannot be in one-to-one correspondence. It is this difference that is mainly responsible for the “odd consequences” mentioned above.
Now that we have established that some sets that seem smaller or larger than ℕ, such as the squares or the integers, are actually countable, let us turn to a set that seems “much larger,” namely ℚ. How could we hope to list all the rationals? After all, between any two of them you can find infinitely many others, so it seems hard not to leave some of them out when you try to list them. However, remarkable as it may seem, it is possible to list the rationals. The key idea is that listing the rationals whose numerator and denominator are both smaller (in modulus) than some fixed number k is easy, as there are only finitely many of them. So we go through in order: first when both numerator and denominator are at most 1, then when they are at most 2, and so on (being careful not to relist any number, so that for example  should not also appear as
should not also appear as 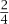 or
or 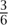 ). This leads to an ordering such as 0, 1, -1,2, -2,
). This leads to an ordering such as 0, 1, -1,2, -2,  , -
, -  , 3, -3,
, 3, -3, 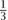 , -
, -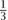 ,
, 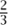 , -
, - 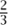 ,
, 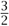 , -
, - 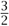 , 4, -4, . . . .
, 4, -4, . . . .
We could use the same idea to list sets that look even larger, such as, for example, the algebraic numbers (all real numbers, such as 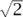 , that satisfy a polynomial equation with integer coefficients). Indeed, we note that each polynomial has only finitely many roots (which are therefore listable), so all we need to do is list the polynomials (as then we can go through them, in order, listing their roots). And we can do that by applying the same technique again: for each d we list those polynomials of degree at most d that we have not already listed, with coefficients that are at most d in modulus.
, that satisfy a polynomial equation with integer coefficients). Indeed, we note that each polynomial has only finitely many roots (which are therefore listable), so all we need to do is list the polynomials (as then we can go through them, in order, listing their roots). And we can do that by applying the same technique again: for each d we list those polynomials of degree at most d that we have not already listed, with coefficients that are at most d in modulus.
Based on the above examples, one might well guess that every infinite set is countable. But a beautiful argument of CANTOR [VI.54], called his “diagonal” argument, shows that the real numbers are not countable. We imagine that we have a list of all real numbers, say rl, r2, r3, . . . . Our aim is to show that this list cannot possibly contain all the reals, so we wish to construct a real that is not on this list. How do we accomplish this? We have each ri written as an infinite decimal, say, and now we define a new number s as follows. For the first digit of s (after the decimal point), we choose a digit that is not the first digit of r1. Note that this already guarantees that s cannot equal r1. (To avoid coincidences with recurring 9s and the like, it is best to choose this first digit of s not to be 0 or 9 either.) Then, for the second digit of s, we choose a digit that is not the second digit of r2; this guarantees that s cannot be equal to r2. Continuing in this way, we end up with a real number s that is not on our list: whatever n is, the number s cannot be rn, as s and rn differ in the nth decimal place!
One can use similar arguments any time that we have “an infinite number of independent choices” to make in specifying an object (like the various digits of s). For example, let us use the same ideas to show that the set of all subsets of ℕ is uncountable. Suppose we have listed all the subsets as A1, A2, A3, . . . . We will define a new set B that is not equal to any of the An. So we include the point 1 in B if and only if 1 does not belong to A1 (this guarantees that B is not equal to A1), and we include 2 in B if and only if 2 does not belong to A2, and so on. It is amusing to note that one can write this set B down as {n ∈ ℕ: n ∉ An}, which shows a striking resemblance to the set in Russell’s paradox.
Countable sets are the “smallest” infinite sets. However, the set of real numbers is by no means the “largest” infinite set. Indeed, the above argument shows that no set X can be put into one-to-one correspondence with the set of all its subsets. So the set of all subsets of the real numbers is “strictly larger” than the set of real numbers, and so on.
The notion of countability is often a very fruitful one to bear in mind. For example, suppose we want to know whether or not all real numbers are algebraic. It is a genuinely hard exercise to write down a particular real that is TRANSCENDENTAL [III.41] (meaning not algebraic; see LIOUVILLE’S THEOREM AND ROTH’S THEOREM [V.22] for an idea of how it can be done), but the above notions make it utterly trivial that transcendental numbers exist. Indeed, the set of all real numbers is uncountable but the set of algebraic numbers is countable! Furthermore, this shows that “most” real numbers are transcendental: the algebraic numbers form only a tiny proportion of the reals.
1. For sufficiently nice sets of integers there is a definition of “density” that can be useful too. According to this definition, the even numbers have density  , while the squares and the primes have density 0, as one might expect. However, this is not the notion of size under discussion here.
, while the squares and the primes have density 0, as one might expect. However, this is not the notion of size under discussion here.