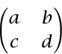
The determinant of a 2 × 2 matrix
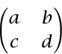
is defined to be ad - bc. The determinant of a 3 × 3 matrix
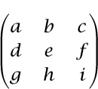
is defined to be aei+bfg+cdh -afh -bdi -ceg. What do these expressions have in common, how do they generalize, and why is the generalization significant?
To begin with the first question, let us make a few simple observations. Both expressions are sums and differences of products of entries from the matrix. Each one of these products contains exactly one element from each row of the matrix and also exactly one element from each column. In both cases, a minus sign seems to attach itself to the products for which the entries selected from the matrix “slope upward” rather than “downward.”
Up to a point it is easy to see how to extend this definition to n × n matrices with n ≥ 4. We simply take sums and differences of all possible products of n entries, where one entry from each row is used and one from each column. The difficulty comes in deciding which of these products to add and which to subtract. To do this we take one of the products and use it to define a permutation σ of the set { 1, 2, . . . , n} as follows. For each i ≤ n, the product contains exactly one entry in the ith row. If it belongs to the jth column then σ (i) = j. The product is added if this permutation is even and subtracted if it is odd (see PERMUTATION GROUPS [III.68]). So, for example, the permutation corresponding to the entry afh in the 3 × 3 determinant above sends 1 to 1, 2 to 3, and 3 to 2. This is an odd permutation, which is why afh receives a minus sign.
We still need to explain why the particular choice of products and minus signs that we have just defined is important. The reason is that it tells us something about the effect of a matrix when it is considered as a linear map. Let A be an n × n matrix. Then, as explained in [I.3 §3.2], A specifies a linear map α from ℝn to ℝn. The determinant of A tells us what this linear map does to volumes. More precisely, if X is a subset of ℝn with n-dimensional volume V, then αX, the result of transforming X using the linear map α, will have volume V times the determinant of A. We could write this symbolically as follows:
vol((αX) = detA . vol(X).
For example, consider the 2 × 2 matrix
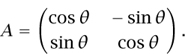
The corresponding linear map is a rotation of ℝ2 through an angle of θ. Since rotating a shape does not affect its volume, we should expect the determinant of A to be 1, and sure enough it is cos2 θ + sin2 θ, which is 1 by Pythagoras’s theorem.
The above explanation is a slight oversimplification in one respect: determinants can be negative, but clearly volumes cannot. If the determinant of a matrix is -2, to give an example, it means that the linear map multiplies volumes by 2 but also “turns shapes inside out” by reflecting them.
Determinants have many useful properties, which become obvious once one knows the above interpretation in terms of volumes. (However, it is much less obvious that this interpretation is correct: in setting up the theory of determinants one must do some work somewhere.) Let us give three of these properties.
(i) Let V be a VECTOR SPACE [I.3 §2.3] and let α: V → V be a linear map. Let v1, . . . , vn be a basis of V and let A be the matrix of α with respect to this basis. Now let w1, . . . , wn be another basis of V and let B be the matrix of α with respect to this different basis. Then A and B are different matrices, but since they both represent the linear map α, they must have the same effect on volumes. It follows that det(A) = det(B). To put this another way: the determinant is better thought of as a property of linear maps rather than of matrices.
Two matrices that represent the same linear map in the above sense are called similar. It turns out that A and B are similar if and only if there is an invertible matrix P such that P-1AP = B. (An n × n matrix P is invertible if there is a matrix Q such that PQ equals the n × n identity matrix, In, which turns out to imply that QP equals In as well. If this is true, then Q is called the inverse of P and is denoted P-1.) What we have just shown is that similar matrices have the same determinant.
(ii) If A and B are any two n × n matrices, then they represent linear maps α and β of ℝn. The product AB represents the linear map αβ: that is, the linear map that results from doing β followed by α Since β multiplies volumes by det B and α multiplies them by det A, αβ multiplies them by det A det B. It follows that det(AB) = detA detB. (The determinant of a product equals the product of the determinants.)
(iii) If A is a matrix with determinant 0 and B is any other matrix, then AB will have determinant 0 as well, by the multiplicative property just discussed. It follows that AB cannot equal In, since In has determinant 1. Therefore a matrix with determinant 0 is not invertible. The converse of this turns out to be true as well: a matrix with nonzero determinant is invertible. Thus, the determinant gives us a way of finding out whether a matrix can be inverted.