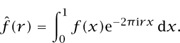
If f : ℝ → ℝ is a periodic function with period 1, then one can obtain a great deal of useful information about f by calculating its Fourier coefficients (see THE FOURIER TRANSFORM [III.27] for a discussion Of why). This is true for both theoretical and practical reasons, and because of the latter it is highly desirable to have a good way of computing Fourier coefficients quickly. A method for doing this was discovered by Cooley and Tukey in 1965 (though it turned out that Gauss had anticipated them over 150 years earlier).
The rth Fourier coefficient of f is given by the formula
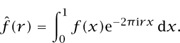
If we do not have an explicit formula for the integral (as would be the case, for instance, if f were derived from some physical signal rather than a mathematical formula), then we will want to approximate this integral numerically, and a natural way to do that is to discretize it: that is, turn it into a sum of the form 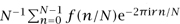 . If f is not too wildly oscillating and r is not too big, then this should be a good approximation.
. If f is not too wildly oscillating and r is not too big, then this should be a good approximation.
The sum above will be unchanged if we add a multiple of N to r, so we now care only about the values of f at points of the form n/N. Moreover, the periodicity of f tells us that adding a multiple of N to n also makes no difference. So we can regard both n and r as belonging to the group ℤN of integers mod N (see MODULAR ARITHMETIC [III.58]). Let us change our notation to one that reflects this. Given a function g defined on ℤN we define the discrete Fourier transform of g to be the function ĝ, also defined on ℤN, which is given by the formula

where we are writing ω for e2πi/N, so that ω- rn = e- 2πirn/N. Note that the sum over n could be regarded as a sum from 0 to N - 1 just as above; the other notational change is that we have written g(n) instead of f (n/N).
The discrete Fourier transform can be thought of as multiplying a column vector (corresponding to the function g) by an N × N matrix (with entries N-1 ω-rn for each r and n). Therefore it can be calculated using about N2 arithmetical operations. The fast Fourier transform arises from the observation that the sum in (1) has symmetry properties that allow it to be calculated much more efficiently. This is most easily seen when N is a power of 2, and to make it even easier we shall look at the case N = 8. The sums to be evaluated are then
g(0) + ω-r g(1) + ω-2r g(2) + · · · + ω-7r g(7)
for each r between 0 and 7. Now a sum like this can be rewritten as
g(0) + ω-2r g(2) + ω-4r g(4) + ω-6r g(6)
+ ω-r(g(1)+ ω-2r g(3) + ω-4r g(5) + ω-6r g(7)),
which is interesting because
g(0) + ω-2r g(2) + ω- 4r g(4) + ω- 6r g(6)
and
g(1) + ω-2r g(3) + ω-4r g(5) + ω-6r g(7)
are themselves values of discrete Fourier transforms. For instance, if we set h(n) = g(2n) for 0 ≥ n ≥ 3, and write ψ for ω2 = e2πi/4, then the first expression equals h(0) + ψ-r h(1) + ψ-2r h(2) + ψ-3r h(3). If we think of h as being defined on ℤ4, then this is precisely the formula for 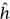 (r).
(r).
A similar remark applies to the second expression, so if we can calculate the discrete Fourier transforms of the “even part” of g and the “odd part” of g, then it will be very straightforward to obtain each value of the Fourier transform of g itself: it will be a linear combination of values of the transforms of the two parts of g. Thus, if N is even and we write F(N) for the number of operations needed to calculate the discrete Fourier transform of a function defined on ℤN, we obtain a recurrence of the form
F(N) = 2F(N/2) + CN.
The interpretation of this is that in order to work out the N values of the transform of a function on ℤN, it is enough to work out two such transforms for functions on ℤN/2 and work out N linear combinations, each of which takes a constant number of steps.
If N is a power of 2, then we can iterate this: F(N/2) will be at most 2F(N/4) + CN/2, and so on. It is not hard to show as a result that F(N) is at most CN log N for some constant C, a considerable improvement on CN2. If N is not a power of 2, then the above argument does not work, but there are modifications of the method that do, and that lead to similar efficiency gains. (Indeed, this is true for the Fourier transform on an arbitrary finite Abelian group.)
Once we can calculate Fourier transforms efficiently, there are other calculations that immediately become easy as well. A simple example is the inverse Fourier transform, which has a formula very similar to that of the Fourier transform and can therefore be calculated in a similar way. Another calculation that becomes easy is the convolution of two sequences, which is defined as follows. If a = (a0, a1, a2,. . . , am) and b = (b0, b1, b2, . . . , bn) are two sequences, then their convolution is the sequence c = (c0, cl, c2, . . . , cm+n), where each cr is defined to be a0br + a1br-1 + · · · + arb0. This sequence is denoted by a * b. One of the most important properties of Fourier transforms is that they “convert convolutions into multiplication.” That is, if we find a suitable way of regarding a and b as functions on ℤN, then the Fourier transform of a * b is the function r ↦ â (r) 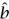 (r). Therefore, to work out a* b we can work out â and
(r). Therefore, to work out a* b we can work out â and 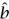 , multiply them together for each r, and take the inverse Fourier transform of the result. All stages of this calculation are quick, so calculating convolutions is quick.
, multiply them together for each r, and take the inverse Fourier transform of the result. All stages of this calculation are quick, so calculating convolutions is quick.
This immediately leads to a quick way of multiplying the two polynomials a0 + al x + · · · + am xm and b0+bix+ · · · + bnxn together, since the coefficients of the product are given by the sequence c = a * b. If all the ai are between 0 and 9, it is a quick process to evaluate the product polynomial at x = 10 (since none of the coefficients cr will have many digits), so we also have a method of multiplying two n-digit integers together that is far faster than long multiplication. These are two of the huge number of applications of the fast Fourier transform. A more direct source of applications occurs in engineering, where one frequently wishes to analyze a signal by looking at its Fourier transform. A very surprising application is to QUANTUM COMPUTATION [III.74]: a famous result of Peter Shor is that one can use a quantum computer to factorize large integers very quickly; this algorithm depends in an essential way on the fast Fourier transform, but uses the power of quantum computing in an almost miraculous way to divide the N log N steps into N lots of log N steps that can be carried out “in parallel.”