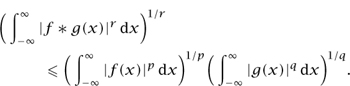III.29 Function Spaces
Terence Tao
1 What Is a Function Space?
When one works with real or complex numbers, there is a natural notion of the magnitude of a number x, namely its modulus |x|. One can also use this notion of magnitude to define a distance |x - y| between two numbers x and y and thereby say in a quantitative way which pairs of numbers are close and which ones are far apart.
The situation becomes more complicated, however, when one deals with objects with more degrees of freedom. Consider for instance the problem of determining the “magnitude” of a three-dimensional rectangular box. There are several candidates for such a magnitude: length, width, height, volume, surface area, diameter (the length of a long diagonal), eccentricity, and so forth. Unfortunately, these magnitudes do not give equivalent comparisons: for example, box A may be longer and have a greater volume than box B, but box B may be wider and have a greater surface area. Because of this, one abandons the idea that there should be only one notion of “magnitude” for boxes, and instead accepts that there is a multiplicity of such notions and that they can all be useful: for some applications one may wish to distinguish the large-volume boxes from the small-volume boxes, while in others one may wish to distinguish the eccentric boxes from the round boxes. Of course, there are several relationships between the different notions of magnitude (e.g., the ISOPERIMETRIC INEQUALITY [IV.26] allows One to place an upper limit on the possible volume if one knows the surface area), so the situation is not as disorganized as it may at first appear.
Now let us turn to functions with a fixed domain and range. (A good case to have in mind is functions f : [-1, 1] →  from the interval [-1,1] to the real line
from the interval [-1,1] to the real line  .) These objects have infinitely many degrees of freedom, so it should not be surprising that there are now infinitely many distinct notions of “magnitude,” which all provide different answers to the question “how large is a given function f?”(or to the closely related question “how close together are two functions f and g?”). In some cases, certain functions may have infinite magnitude by one measure and finite magnitude by another (similarly, a pair of functions may be very close by one measure and very far apart by another). Again, this situation may seem chaotic, but it simply reflects the fact that functions have many distinct characteristics—some are tall, some are broad, some are smooth, some are oscillatory, and so forth—and that, depending on the application at hand, one may need to give more weight to one of these characteristics than to others. In analysis, these characteristics are embodied in a variety of standard function spaces and their associated norms, which are available to describe functions both qualitatively and quantitatively.
.) These objects have infinitely many degrees of freedom, so it should not be surprising that there are now infinitely many distinct notions of “magnitude,” which all provide different answers to the question “how large is a given function f?”(or to the closely related question “how close together are two functions f and g?”). In some cases, certain functions may have infinite magnitude by one measure and finite magnitude by another (similarly, a pair of functions may be very close by one measure and very far apart by another). Again, this situation may seem chaotic, but it simply reflects the fact that functions have many distinct characteristics—some are tall, some are broad, some are smooth, some are oscillatory, and so forth—and that, depending on the application at hand, one may need to give more weight to one of these characteristics than to others. In analysis, these characteristics are embodied in a variety of standard function spaces and their associated norms, which are available to describe functions both qualitatively and quantitatively.
Formally, a function space is a NORMED SPACE [III.62] X, the elements of which are functions (with some fixed domain and range). A majority (but certainly not all) of the standard function spaces considered in analysis are not just normed spaces but also BANACH SPACES [III.62]. The norm || f ||X of a function f in X is the function space’s way of measuring how large f is. It is common, though not universal, for the norm to be defined by a simple formula and for the space X to consist precisely of those functions f for which the resulting definition || f ||X makes sense and is finite. Thus, the mere fact that a function f belongs to a function space X can already convey some qualitative information about that function. For example, it may imply some regularity,1 decay, boundedness, or integrability on the function f. The actual value of the norm || f ||X makes this information quantitative. It may tell us how regular f is, how much decay it has, by which constant it is bounded, or how large its integral is.
2 Examples of Function Spaces
We now present a sample of commonly used function spaces. For simplicity we shall consider only spaces of functions from [-1, 1] to  .
.
2.1 C0[-1, 1]
This space consists of all CONTINUOUS FUNCTIONS [I.3 §5.2] from [-1, 1] to  , and is sometimes denoted C[-1, 1]. Continuous functions are regular enough to allow one to avoid many of the technical subtleties associated with very rough functions. Continuous functions on a COMPACT [III.9] interval such as [-1, 1] are bounded, so the most natural norm to place on this space is the supremum norm, denoted || f ||∞, which is the largest possible value of |f(x)|. (Formally, it is defined to be sup{| f(x)| : x
, and is sometimes denoted C[-1, 1]. Continuous functions are regular enough to allow one to avoid many of the technical subtleties associated with very rough functions. Continuous functions on a COMPACT [III.9] interval such as [-1, 1] are bounded, so the most natural norm to place on this space is the supremum norm, denoted || f ||∞, which is the largest possible value of |f(x)|. (Formally, it is defined to be sup{| f(x)| : x  [-1,1]}, but for continuous functions on [-1, 1] the two definitions are equivalent.)
[-1,1]}, but for continuous functions on [-1, 1] the two definitions are equivalent.)
The supremum norm is the norm associated with uniform convergence: a sequence f1, f2,. . . converges uniformly to f if and only if || fn - f ||∞ tends to 0 as n tends to ∞. The space C0[-1, 1] has the useful property that one can multiply functions together as well as adding them. This makes it a basic example of a Banach algebra.
2.2 C1[-1, 1]
This is a space that has a more restricted membership than C0[-1, 1]: not only must a function f in C1 [-1, 1] be continuous but it must also have a derivative that is continuous. The supremum norm here is no longer a natural one, because a sequence of continuously differentiable functions can converge in this norm to a nondifferentiable function. Instead, the right norm here is the C1-norm || f ||Cl[-1,1], which is defined to be || f ||∞ + || f′ ||∞.
Notice that the C1-norm measures both the size of a function and the size of its derivative. (Merely controlling the latter would be unsatisfactory, since it would give constant functions a norm of zero.) Thus it is a norm that forces a greater degree of regularity than the supremum norm. One can similarly define the space C2[-1, 1] of twice continuously differentiable functions, and so forth, all the way up to the space C∞ [-1, 1] of infinitely differentiable functions. (There are also “fractional” versions of these spaces, such as C0,α[-1, 1], the space of α-Hölder continuous functions. We will not discuss these variants here.)
2.3 The Lebesgue Spaces Lp[-1, 1]
The supremum norm || f ||∞ mentioned earlier gives simultaneous control on the size of | f(x) | for all x  [-1,1]. However, this means that if there is a tiny set of x for which | f(x) | is very large, then || f || ∞ is very large, even if a typical value of | f(x) | is much smaller. It is sometimes more advantageous to work with norms that are less influenced by the values of a function on small sets. The Lp-norm of a function f is
[-1,1]. However, this means that if there is a tiny set of x for which | f(x) | is very large, then || f || ∞ is very large, even if a typical value of | f(x) | is much smaller. It is sometimes more advantageous to work with norms that are less influenced by the values of a function on small sets. The Lp-norm of a function f is
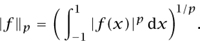
This is defined for 1 ≤ p < ∞ and for any measurable f. The function space Lp [-1, 1] is the class of measurable functions for which the above norm is finite. The norm || f||∞ of a measurable function f is its essential supremum: roughly speaking this means the largest value of | f(x) | if you ignore sets of measure zero. It turns out to be the limit of the norms || f ||p as p tends to infinity. The space L∞[-1, 1] consists of those measurable functions f for which || f ||∞ is finite. While the L∞ norm is concerned solely with the “height” of a function, the Lp norms are instead concerned with a combination of the “height’ and “width” of a function.
Particularly important among these norms is the L2-norm, since L2[-1, 1] is a HILBBRT SPACE [III.37]. This space is exceptionally rich in symmetries: there is a wide variety of unitary transformations, that is, invertible linear maps T defined on L2[-1, 1] such that || Tf ||2 = || f ||2 for every function f  L2[-1, 1].
L2[-1, 1].
2.4 The Sobolev Spaces Wk,p[-1, 1]
The Lebesgue norms control, to some extent, the height and width of a function, but say nothing about regularity; there is no reason why a function in Lp should be differentiable or even continuous. To incorporate such information one often turns to the Sobolev norms || f ||wkp[-1,1], defined for 1 ≤ p ≤ ∞ and k ≥ 0 by
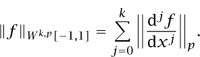
The Sobolev space Wk,p[-1,1 ] is the space of functions for which this norm is finite. Thus, a function lies in Wk,p[-1, 1] if it and its first k derivatives all belong to Lp[-1,1]. There is one subtlety: we do not require f to be k times differentiable in the usual sense, but in the weaker sense of DISTRIBUTIONS [III.18]. For instance, the function f(x) = |x| is not differentiable at zero, but it does have a natural weak derivative: the function f′(x) which is -1 when x < 0 and +1 when x > 0. This function lies in L∞[-1,1] (since the set {0} has measure zero, we do not need to specify f′(0)), and therefore f lies in W1,∞[-1,1] (which turns out to be the space of Lipschitz-continuous functions). We need to consider these generalized differentiable functions because without them the space Wk,p[-1, 1] would not be complete.
Sobolev norms are particularly natural and useful in the analytical study of partial differential equations and mathematical physics. For instance, the W1,2 norm can be interpreted as (the square root of) an “energy” associated with a function.
3 Properties of Function Spaces
There are many ways in which knowledge of the structure of function spaces can assist in the study of functions. For instance, if one has a good basis for the function space, so that every function in the space is a (possibly infinite) linear combination of basis elements, and one has some quantitative estimates on how this linear combination converges to the original function, then this allows one to represent that function efficiently in terms of a number of coefficients, and also allows one to approximate that function by smoother functions. For instance, one basic result about L2[-1,1] is the Plancherel theorem, which asserts, among other things, that there are numbers (an) = - ∞ such that
= - ∞ such that
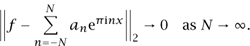
This shows that any function in L2[-1, 1] can be approximated to any desired accuracy in L2 by a trigonometric polynomial: that is, an expression of the form 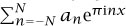 The number an is the n th Fourier coefficient
The number an is the n th Fourier coefficient 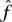 (n) of f. It is given by the formula
(n) of f. It is given by the formula
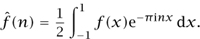
One can regard this result as saying that the functions eπinx form a very good basis for L2 [-1,1]. (They are in fact an orthonormal basis: they have norm 1 and the inner product of two different ones is always zero.)
Another very basic fact about function spaces is that certain function spaces embed into others, so that a function from one space automatically also belongs to other spaces. Furthermore, there is often some inequality that gives an upper bound for one norm in terms of another. For instance, a function in a high-regularity space such as C1[-1, 1] automatically belongs to a low-regularity space such as C0[-1,1], and a function in a high-integrability space such as L∞[-1, 1] automatically belongs to a low-integrability space such as L1[-1, 1]. (This statement is no longer true if one replaces the interval [-1, 1] by a set of infinite measure, such as the real line  .) These inclusions cannot be reversed; however, one does have the Sobolev embedding theorem, which allows one to “trade” regularity for integrability. This result tells us that spaces with lots of regularity but low integrability can be embedded into spaces with low regularity but high integrability. A sample estimate of this type is
.) These inclusions cannot be reversed; however, one does have the Sobolev embedding theorem, which allows one to “trade” regularity for integrability. This result tells us that spaces with lots of regularity but low integrability can be embedded into spaces with low regularity but high integrability. A sample estimate of this type is
|| f ||∞ ≤ || f ||W1,1[-1,1],
which tells us that if the integrals of |f(x)| and | f′(x) | are both finite, then f must be bounded (which is a far stronger integrability condition than the finiteness of || f ||1).
Another very useful concept is that of DUALITY [III.19]. Given a function space X, one can define the dual space X*, which is formally defined as the class of all continuous 1inear functionals on X, or more precisely all maps ω : X →  (or ω : X →
(or ω : X →  , if the function space is complex valued) that are linear and continuous with respect to the norm of X. For example, it turns out that every linear functional ω on the space Lp[-1, 1] is of the form
, if the function space is complex valued) that are linear and continuous with respect to the norm of X. For example, it turns out that every linear functional ω on the space Lp[-1, 1] is of the form
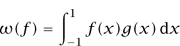
for some function g in Lq [-1, 1], where q is the dual or conjugate exponent of p, defined by the equation 1/p+ 1/q = 1.
One can sometimes analyze functions in a function space by looking instead at how the linear functionals in the dual space act on those functions. Similarly, one can often analyze a continuous linear operator T : X → Y from one function space to another by first considering the adjoint operator T* : Y* →. X*, defined for all linear functionals ω : Y →  by letting T* ω be the functional on X defined by the formula T*ω(x) = ω(Tx).
by letting T* ω be the functional on X defined by the formula T*ω(x) = ω(Tx).
We mention one more important fact about function spaces, which is that certain function spaces X “interpolate” between two other function spaces X0 and X1. For example, there is a natural sense in which the spaces Lp[-1, 1] with 1 < p < ∞ “lie between” the spaces L1[-1, 1] and L∞ [-1, 1]. The precise definition of interpolation is too technical for this article, but its usefulness lies in the fact that the “extreme” spaces X0 and X1 are often easier to deal with than the “intermediate” spaces X. For this reason, it is sometimes possible to prove difficult results about X by proving much easier results about X0 and X1 and “interpolating” between them. For instance, it can be used to give a short proof of Young’s inequality, which is the following statement. Let 1 ≤ p, q, r ≤ ∞ satisfy the equation 1/p+ 1/q = 1/r + 1, let f and g belong to Lp ( ) and Lq(
) and Lq( ), respectively, and let f *g be the convolution of f and g: that is, f * g(x) =
), respectively, and let f *g be the convolution of f and g: that is, f * g(x) = 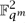 f (y)g(x - y)dy. Then
f (y)g(x - y)dy. Then
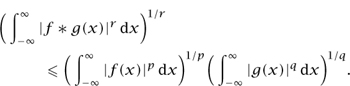
Interpolation is useful here because the inequality is easy to prove in the extreme cases when p = 1, when q = 1, or when r = ∞. It is much harder to prove this result without the help of interpolation theory.
 from the interval [-1,1] to the real line
from the interval [-1,1] to the real line  .) These objects have infinitely many degrees of freedom, so it should not be surprising that there are now infinitely many distinct notions of “magnitude,” which all provide different answers to the question “how large is a given function f?”(or to the closely related question “how close together are two functions f and g?”). In some cases, certain functions may have infinite magnitude by one measure and finite magnitude by another (similarly, a pair of functions may be very close by one measure and very far apart by another). Again, this situation may seem chaotic, but it simply reflects the fact that functions have many distinct characteristics—some are tall, some are broad, some are smooth, some are oscillatory, and so forth—and that, depending on the application at hand, one may need to give more weight to one of these characteristics than to others. In analysis, these characteristics are embodied in a variety of standard function spaces and their associated norms, which are available to describe functions both qualitatively and quantitatively.
.) These objects have infinitely many degrees of freedom, so it should not be surprising that there are now infinitely many distinct notions of “magnitude,” which all provide different answers to the question “how large is a given function f?”(or to the closely related question “how close together are two functions f and g?”). In some cases, certain functions may have infinite magnitude by one measure and finite magnitude by another (similarly, a pair of functions may be very close by one measure and very far apart by another). Again, this situation may seem chaotic, but it simply reflects the fact that functions have many distinct characteristics—some are tall, some are broad, some are smooth, some are oscillatory, and so forth—and that, depending on the application at hand, one may need to give more weight to one of these characteristics than to others. In analysis, these characteristics are embodied in a variety of standard function spaces and their associated norms, which are available to describe functions both qualitatively and quantitatively. [-1,1]}, but for continuous functions on [-1, 1] the two definitions are equivalent.)
[-1,1]}, but for continuous functions on [-1, 1] the two definitions are equivalent.)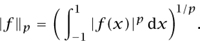
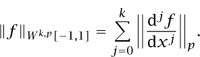
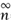 = - ∞ such that
= - ∞ such that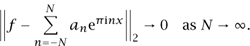
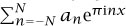 The number an is the n th Fourier coefficient
The number an is the n th Fourier coefficient 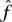 (n) of f. It is given by the formula
(n) of f. It is given by the formula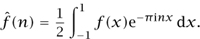
 , if the function space is complex valued) that are linear and continuous with respect to the norm of X. For example, it turns out that every linear functional ω on the space Lp[-1, 1] is of the form
, if the function space is complex valued) that are linear and continuous with respect to the norm of X. For example, it turns out that every linear functional ω on the space Lp[-1, 1] is of the form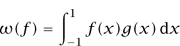
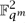 f (y)g(x - y)dy. Then
f (y)g(x - y)dy. Then