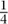n2 is possible, at least if n is even, since one can then divide up the n vertices into two equal classes and join all vertices in one class to all vertices in the other. But can there be more edges than that?A graph is one of the simplest of all mathematical structures: it consists of some elements called vertices (of which there are usually just finitely many), some pairs of which are deemed to be “joined” or “adjacent.” It is customary to represent the vertices by points in a plane and to join adjacent points by a line. The line is referred to as an edge (though how the line is drawn or visualized is irrelevant: all that is important is whether or not two points are joined).
For example, the rail network of a country can be represented by a graph: we can use vertices to represent the stations, and we can join two vertices if they represent consecutive stations along some railroad. Another example is provided by the Internet: the vertices are all the world’s computers, and two are adjacent if there is a direct link between them.
Many questions in graph theory take the form of asking what some structural property of a graph can tell you about its other properties. For example, suppose that we are trying to find a graph with n vertices that does not contain a triangle (defined to be a set of three vertices that are mutually joined). How many edges can the graph have? Clearly 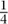n2 is possible, at least if n is even, since one can then divide up the n vertices into two equal classes and join all vertices in one class to all vertices in the other. But can there be more edges than that?
Here is another example of a typical question about graphs. Let k be a positive integer. Must there exist an n such that every graph with n vertices always contains either k vertices that are all joined to each other or k vertices no two of which are joined to each other? This question is quite easy for k = 3 (where n = 6 suffices), but already for k = 4 it is not obvious that such an n exists.
For more on these problems (the first is the founding problem of “extremal graph theory,” while the second is the founding problem of “Ramsey theory”) and on the study of graphs in general, see EXTREMAL AND PROBABILISTIC COMBINATORICS [IV.19].