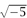 with a and b integers, one can factorize 6 either as 2 × 3 or as (1 +
with a and b integers, one can factorize 6 either as 2 × 3 or as (1 + 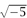 )(1 -
)(1 -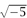 ).
).THE FUNDAMENTAL THEOREM OF ARITHMETIC [V.14] asserts that every positive integer can be written in exactly one way (apart from reordering) as a product of primes. Analogous theorems are true in other contexts as well: for example, there is a unique factorization theorem for polynomials, and another one for Gaussian integers, that is, numbers of the form a + ib where a and b are integers.
However, for most NUMBER FIELDS [III.63], the associated “ring of integers” does not have the unique-factorization property. For example, in the RING [III.81 §1] of numbers of the form a + b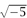 with a and b integers, one can factorize 6 either as 2 × 3 or as (1 +
with a and b integers, one can factorize 6 either as 2 × 3 or as (1 + 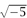 )(1 -
)(1 -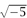 ).
).
The ideal class group is a way of measuring how badly unique factorization fails. Given any ring of integers of a number field, one can define a multiplicative structure on its set of IDEALS [III.81 §2], for which unique factorization holds. The elements of the ring itself correspond to so-called “principal ideals,” so if every ideal is principal, then unique factorization holds for the ring. If there are nonprincipa1 ideals, then one can define a natural EQUIVALENCE RELATION [I.2 §2.3] on them in such a way that the equivalence classes, which are called ideal classes, form a GROUP [I.3 §2.1]. This group is the ideal class group. All principal ideals belong to the class that forms the identity of this group, so the larger and more complex the ideal group is, the further the ring is from having the unique-factorization property. For more details, see ALGEBRAIC NUMBERS [IV.1], and in particular section 7.