III.45 K-Theory
K-theory concerns one of the most important invariants of a TOPOLOGICAL SPACE [III.90] X, a pair of groups called the K-groups of X. To form the group K0(X) one takes all (equivalence classes of) vector bundles on X, and uses the direct sum as the group operation. This leads not to a group but to a semigroup. However, from the semigroup one can easily construct a group in the same way that one constructs  out of
out of 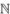 : by taking equivalence classes of expressions of the form a - b. If i is a positive integer, then there is a natural way of defining a group K-i(X): it is closely related to the group K0(Si × X). The very important Bott periodicity theorem says that Ki(X) depends only on the parity of i, so there are in fact just two distinct K-groups, K0(X) and K1(X). See ALGEBRAIC TOPOLOGY [IV.6 §6] for more details.
: by taking equivalence classes of expressions of the form a - b. If i is a positive integer, then there is a natural way of defining a group K-i(X): it is closely related to the group K0(Si × X). The very important Bott periodicity theorem says that Ki(X) depends only on the parity of i, so there are in fact just two distinct K-groups, K0(X) and K1(X). See ALGEBRAIC TOPOLOGY [IV.6 §6] for more details.
If X is a topological space such as a compact manifold, then one can associate with it the C*-algebra C(X) of all continuous functions from X to ℂ. It turns out to be possible to define the K-groups in terms of this algebra in such a way that it applies to algebras that are not of the form C(X). In particular, it applies to algebras where multiplication is not commutative. For instance, K-theory provides important invariants of C*-algebras. See OPERATOR ALGEBRAS [IV.15 §4.4].
Lagrange Multipliers
See OPTIMIZATION AND LAGRANGE MULTIPLIERS [III.64]
 out of
out of 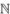 : by taking equivalence classes of expressions of the form a - b. If i is a positive integer, then there is a natural way of defining a group K-i(X): it is closely related to the group K0(Si × X). The very important Bott periodicity theorem says that Ki(X) depends only on the parity of i, so there are in fact just two distinct K-groups, K0(X) and K1(X). See ALGEBRAIC TOPOLOGY [IV.6 §6] for more details.
: by taking equivalence classes of expressions of the form a - b. If i is a positive integer, then there is a natural way of defining a group K-i(X): it is closely related to the group K0(Si × X). The very important Bott periodicity theorem says that Ki(X) depends only on the parity of i, so there are in fact just two distinct K-groups, K0(X) and K1(X). See ALGEBRAIC TOPOLOGY [IV.6 §6] for more details.