III.46 The Leech Lattice
To define a lattice in 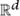 one chooses d linearly independent vectors υ1, . . . , υd and takes all combinations of the form a1υ1 + · · · + adυd, where a1, . . . , ad are integers. For example, to define the hexagonal lattice in
one chooses d linearly independent vectors υ1, . . . , υd and takes all combinations of the form a1υ1 + · · · + adυd, where a1, . . . , ad are integers. For example, to define the hexagonal lattice in 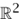 one can take υ1 and υ2 to be (1, 0) and
one can take υ1 and υ2 to be (1, 0) and 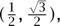 respectively. Notice that υ2 is υ1 rotated by π/3, and also that υ2 - υ1 is υ2 rotated by π/3. Continuing this process, one can generate all the points in a regular hexagon about the origin.
respectively. Notice that υ2 is υ1 rotated by π/3, and also that υ2 - υ1 is υ2 rotated by π/3. Continuing this process, one can generate all the points in a regular hexagon about the origin.
The hexagonal lattice is unusual, among lattices in 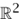 , in that it has a rotational symmetry of order 6. This makes it the “best” lattice in many ways. (For example, bees arrange their hives in hexagonal lattices, soap bubbles of similar sizes naturally organize themselves into hexagonal lattices, and so on.) The Leech lattice plays a similar role in twenty-four dimensions: it is the “most symmetrical” of all twenty-four-dimensional lattices, with a degree of symmetry that is quite extraordinary. It is discussed in more detail in THE GENERAL GOALS OF MATHEMATICAL RESEARCH [I.4 §4].
, in that it has a rotational symmetry of order 6. This makes it the “best” lattice in many ways. (For example, bees arrange their hives in hexagonal lattices, soap bubbles of similar sizes naturally organize themselves into hexagonal lattices, and so on.) The Leech lattice plays a similar role in twenty-four dimensions: it is the “most symmetrical” of all twenty-four-dimensional lattices, with a degree of symmetry that is quite extraordinary. It is discussed in more detail in THE GENERAL GOALS OF MATHEMATICAL RESEARCH [I.4 §4].
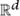 one chooses d linearly independent vectors υ1, . . . , υd and takes all combinations of the form a1υ1 + · · · + adυd, where a1, . . . , ad are integers. For example, to define the hexagonal lattice in
one chooses d linearly independent vectors υ1, . . . , υd and takes all combinations of the form a1υ1 + · · · + adυd, where a1, . . . , ad are integers. For example, to define the hexagonal lattice in 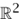 one can take υ1 and υ2 to be (1, 0) and
one can take υ1 and υ2 to be (1, 0) and 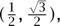 respectively. Notice that υ2 is υ1 rotated by π/3, and also that υ2 - υ1 is υ2 rotated by π/3. Continuing this process, one can generate all the points in a regular hexagon about the origin.
respectively. Notice that υ2 is υ1 rotated by π/3, and also that υ2 - υ1 is υ2 rotated by π/3. Continuing this process, one can generate all the points in a regular hexagon about the origin.