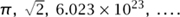
Suppose we are given a sequence of numbers such as
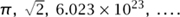
How can we package up this sequence into one object that remembers everything about the sequence, and that might even give us new insights into the sequence? One standard technique is to use a GENERATING FUNCTION [III.32], but here is another way, which has proved very fruitful in number theory and elsewhere. Given a sequence a1, a2, a3, . . . , we define the Dirichlet series
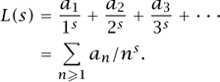
Here, s could be a positive integer, or a real number, for example. As long as our sequence a1, a2, . . . does not grow too quickly (which we shall henceforth assume), the series L(s) will converge for all sufficiently large values of s. Moreover, it may be a very “rich” object, even if the initial sequence is simple. For example, if an = 1 for all n, then the resulting function L(s) is the famous RIEMANN ZETA FUNCTION [IV.2 §3] ζ(s) = 1-s + 2-s + 3-s + · · · , which converges when s > 1 and was shown by Euler to satisfy the following identities, among others (there is one for each even number):
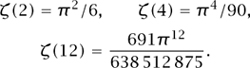
Thus, even a sequence as simple as 1, 1, 1, . . . leads us to some natural questions that cry out to be answered.
The zeta function is the prototypical example of an L-function. However, not every Dirichlet series deserves to be called an L-function. We will mention below some “good” properties that the zeta function has: roughly speaking, a Dirichlet series is considered to be an L-function if it has these good properties. This is not a formal definition of course, but in fact there is no formal definition of “an L-function.” (People have tried to give one, but there is no real consensus about what the right definition should be.) What happens in practice is that a mathematician finds a way of associating a sequence a1, a2, . . . of numbers with a mathematical object X, and if evidence then emerges to suggest that the associated Dirichlet series L(s) shares the good properties of the zeta function, then L(s) will be called the L-function of X.
One can check that the zeta function can also be expressed as an infinite product over primes ζ(s) = Πp(1 - p-s)-1. The product is usually referred to as an Euler product, and if a Dirichlet series is to deserve the title of L-function, then it should have some kind of analogous product expansion. The existence of such an expansion is closely related to, but a little stronger than, the property that the sequence a1, a2, . . . should be multiplicative, which means that amn = aman whenever m and n are coprime.
To go further we must expand our horizons. It is not hard to show that our definition of L(s) makes sense even when s is a complex number, as long as it has a sufficiently large real part. Moreover, it defines a HOLOMORPHIC FUNCTION [I.3 §5.6] in the region of the complex plane where the sum converges. For example, the Dirichlet series defining the zeta function converges for every s such that Re(s) > 1. A standard fact about the zeta function is that it has a unique extension to a holomorphic function of s for any complex number s ≠ 1. This phenomenon is known as meromorphic continuation of the zeta function. It is similar to the fact that the infinite sum 1 + x + x2 + x3 + · · · converges only when |x| < 1 but, when rewritten as 1/(1 - x), has a natural interpretation for any complex number x other than 1. A meromorphic continuation is another of the properties that one would expect of a general L-function. It is important to stress, however, that extending a Dirichlet series to a function on the whole complex plane is not a “purely formal” technique: for a random sequence a1, a2, . . . there is no reason at all for the associated Dirichlet series L(s) to have a natural extension beyond the region where the series converges. The existence of a meromorphic continuation is somehow a rigorous way of asserting the existence of subtle symmetries in the series.
While on the subject of meromorphic continuation, we should briefly mention the RIEMANN HYPOTHESIS [V.26], a conjecture which states that, once one has extended ζ(s) to a function on the whole complex plane, the complex numbers s such that 0 < Re(s) < 1 and ζ(s) = 0 all have real part equal to  . There are analogous Riemann hypotheses for many L-functions, almost all of which are open problems.
. There are analogous Riemann hypotheses for many L-functions, almost all of which are open problems.
The final property we shall emphasize is that there is a relatively simple formula relating ζ(s) and ζ(1 - s). This relation is called the functional equation of the zeta function, and any Dirichlet series worthy of the name L-function should also have an analogous property. (In general one looks for a relation between L(s) and  (k - s), where k is some real number and
(k - s), where k is some real number and  (s) is the Dirichlet series associated with the series of complex conjugates
(s) is the Dirichlet series associated with the series of complex conjugates 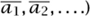
There are many examples of Dirichlet series arising in number theory that do have, or are at least conjectured to have, these three key properties: an Euler product, meromorphic continuation, and a functional equation. These are the Dirichlet series that have come to be known as L-functions. For example, if A and B are integers such that the three roots of the cubic polynomial x3 + Ax + B are distinct, then the equation
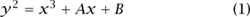
defines an ELLIPTIC CURVE [III.21], and associated with it there is a natural sequence a1, a2, . . . (where an is related to the number of solutions of (1) modulo n, at least when n is prime—see ARITHMETIC GEOMETRY [IV.5 §5.1] for more details). However, it was an open problem for years to establish the existence of a meromorphic continuation of the associated Dirichlet series L(s) to the complex plane: it is now known to exist (and indeed to have no poles) as a consequence of the work of Wiles, Taylor, and others that grew out of the proof of FERMAT’S LAST THEOREM [V.10].
One of the first uses of L-functions was by DIRICHLET [VI.36] himself, who used them to prove that there are infinitely many primes in a general arithmetic progression (see ANALYTIC NUMBER THEORY [IV.2 §4]). In fact, although the Riemann hypothesis is still an open problem, even partial results about the locations of the zeros of the Riemann zeta function have deep consequences in the theory of a distribution of prime numbers.
However, over the last hundred years mathematicians have realized a second use for them: if X is a mathematical object and L(s) is its associated L-function, then there are deep conjectures relating the arithmetic of X to the values that L(s) assumes, typically at points where the Dirichlet series defining L(s) does not converge! Hence, one can investigate X by investigating its L-function. One basic example of this phenomenon is THE BIRCH-SWINNERTON-DYER CONJECTURE [V.4], a weak form of which states that the L-function associated with equation (1) should vanish at s = 1 if and only if (1) has infinitely many solutions such that both x and y are rational numbers. Much is known about this conjecture, and it has been vastly generalized by work of Deligne, Belinson, Bloch, and Kato. However, at the time of writing it remains open.