III.50 Linear Operators and
Their Properties
1 Some Examples of Linear Operators
A LINEAR MAP [I.3 §4.2] between two VECTOR SPACES [I.3 §2.3] V and W is a function T: V → W that satisfies the condition T(λ1υ1 + λ2υ2) = λ1Tυ1 + λ2Tυ2. Two phrases that are used almost interchangeably with “linear map” are “linear transformation” and “linear operator.” The former is often used when one wishes to draw attention to the effect of a linear map on some other object; for example, one might well choose to use the word “transformation” to describe geometrical operations such as reflections or rotations. As for “operator,” it tends to be the word of choice when the linear map is between infinite-dimensional spaces, especially when it is just one of an ensemble of linear maps that form an algebra. It is these maps that we shall discuss here.
Let us begin with some examples of linear operators.
(i) If X is a BANACH SPACE [III.62] whose elements are infinite sequences, then we can define a “shift” S from X to X, which takes the sequence (a1, a2, a3, . . .) to the sequence (0, a1, a2, a3, . . .). (In other words, it puts a 0 at the beginning and shifts the other values of the sequence one place to the right.) The map S is linear, and if the norm on X is not too pathological, then S will be a continuous function from X to X.
(ii) If X is a SPACE OF FUNCTIONS [III.29] defined on the closed interval [0, 1] and w is some fixed function, then the map M that takes the function f to the product f w (which is shorthand for the function x  f (x)w(x)) is linear, and, provided w is small enough in some appropriate sense, M is a continuous linear map from X to X. Such maps are called multipliers. (Note that the property of “being a multiplier” depends not just on the space X and the map M but also on the way we choose to represent X as a space of functions, so it is not an intrinsic property of the map itself.)
f (x)w(x)) is linear, and, provided w is small enough in some appropriate sense, M is a continuous linear map from X to X. Such maps are called multipliers. (Note that the property of “being a multiplier” depends not just on the space X and the map M but also on the way we choose to represent X as a space of functions, so it is not an intrinsic property of the map itself.)
(iii) Another important way of defining linear operators on function spaces is to use a kernel. This is a function K of two variables, which can be used to define a linear map in a way that is similar to the way a matrix can be used to define a map between finite-dimensional vector spaces. The following formula uses K to define a linear map T:
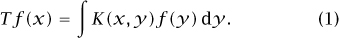
Note the formal similarity between this and the formula
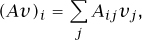
which defines the product of a matrix with a column vector. Once again, K will have to satisfy appropriate conditions in order for (1) to define a continuous linear map.
A good example of a linear operator defined by a kernel is THE FOURIER TRANSFORM [III.2 7] 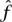 , which takes a function in L2 (
, which takes a function in L2 ( ) to another such function. It is defined by the formula
) to another such function. It is defined by the formula
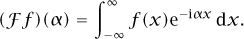
The kernel in this case is the function K(α, x) = e-iαx.
(iv) If f is a differentiable function defined on ℝ, say, and we write Df for its derivative, then we can think of D as a linear map, since D(λf + Δg) = λDf + Δ Dg. In order to regard D as an operator, we need to require f to belong to a suitable function space. The best way of doing this varies from context to context: choosing a good function space can be very important and can raise subtle questions. One way is not to insist that D is defined for every function in the space and not to require D to be continuous: sometimes it is enough if D is discontinuous but defined on a dense set of functions.
Similarly, many partial differential operators, such as the GRADIENT [I.3 § 5.3] and the LAPLACIAN [I.3 § 5.4], are linear operators when viewed appropriately.
2 Algebras of Operators
Although individual operators can be important, linear operators would not be as interesting as they are if it were not for the fact that they can be formed into families. If X is a Banach space, then the set B(X) of all continuous linear operators from X to itself forms a structure known as a Banach algebra. Roughly speaking, this means that it is a Banach space (the norm of an operator T is defined to be the supremum of ||Tx|| over all x such that ||x|| ≥ 1) in which the elements can be multiplied as well as added. The product of T1 and T2 is defined to be the composition T1 T2, and it is easily seen to satisfy the inequality ||T1 T2|| ≤ ||T1|| ||T2||. This algebra is particularly important when X is a WLBERT SPACE [III.37] H: subalgebrss of B(H) have a very rich structure, which is discussed in OPERATOR ALGEBRAS [IV. 15].
3 Properties of Operators Defined on a Hilbert Space
Unlike a general Banach space, a Hilbert space H has an inner product. It is therefore natural to ask that a continuous linear operator from H to H should relate to the inner product somehow. This basic idea leads to several different definitions, each of which picks out an important class of operators.
3.1 Unitary and Orthogonal Maps
Perhaps the most obvious condition one might require of an operator T is that it should preserve the inner product, in the sense that 〈Tx, Ty〉 should equal 〈x,y〉 for any two vectors x and y. In particular, this implies that ||Tx|| = ||x|| for every x, and therefore that T is an isometry (that is, a map that preserves distances). If in addition, T is invertible, which it will be if its image is the whole of H, then T is a unitary map. The unitary maps form a group. If H is n dimensional, then this group is an important LIE GROUP [III.48 §1] called U(n). If H is a real Hilbert space (as opposed to a complex one), then the word “orthogonal” is used instead of “unitary” and the corresponding Lie group is called O(n). When n = 3, orthogonal maps are rotations and reflections, so O(n) is the generalization of the group of rotations and reflections to n dimensions.
3.2 Hermitian and Self-Adjoint Maps
Given any operator T from H to H, there is an operator T* from H to H with the property that 〈Tx,y〉 〈x, T*y〉 for every x and y. This operator is unique, and it is called the adjoint of T. A second property that T can have is that of equaling its own adjoint, which is the case if and only if 〈Tx,y〉 = 〈x, Ty〉 for every x and y. Such operators are called Hermitian or, when the scalars are real, self-adjoint. A simple source of examples of Hermitian maps is multipliers on the space L2 [0, 1], where the function one multiplies by is bounded and real-valued. As we shall see in a moment, there is a sense in which these are the only examples.
3.3 Properties of Matrices
If H is a finite-dimensional space with an orthonormal basis, then we can form the matrix A of T with respect to that basis. The various properties of T discussed above then turn out to be equivalent to properties of the matrix A. The transpose of A is the matrix AT defined by (AT)ij = Aji, and the conjugate transpose is the matrix A* defined by (A*)ij = 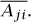 An n × n matrix A is unitary if AA* is the identity, orthogonal if A is real and AAT is the identity, Hermitian if A = A*, and self-adjoint if A = AT (in which case we say that A is symmetric). The operator T has one of these four properties if and only if its matrix A has the corresponding property.
An n × n matrix A is unitary if AA* is the identity, orthogonal if A is real and AAT is the identity, Hermitian if A = A*, and self-adjoint if A = AT (in which case we say that A is symmetric). The operator T has one of these four properties if and only if its matrix A has the corresponding property.
3.4 The Spectral Theorem
Notice that the adjoint of a unitary operator is the inverse of that operator. In particular, both unitary and Hermitian operators commute with their adjoints. An operator with this property is called normal. Normal operators are important because of the famous spectral theorem. If T is a normal operator on a finite- dimensional space H, then the spectral theorem asserts that H has an ORTHONORMAL BASIS [III.37] of eigenvectors of T. In other words, there is a basis of H consisting of orthogonal unit vectors, with the property that the matrix of T with respect to this basis is diagonal. This is an extremely useful theorem in linear algebra. In general, if T is a normal operator on a Hilbert space H, then the spectral theorem tells us that there is something like a “basis” for H, with respect to which T is a multiplier. To put this slightly differently, there is an isometric isomorphism  from H to a Hilbert space H´ of functions that are square-integrable with respect to some MEASURE [III.55], and the map
from H to a Hilbert space H´ of functions that are square-integrable with respect to some MEASURE [III.55], and the map  T
T -1 is a multiplier on H´.
-1 is a multiplier on H´.
3.5 Projections
Another important class of maps on a Hilbert space is the set of orthogonal projections. In general, an element T of an algebra is an idempotent if it has the property that T2 = T. If the algebra is an algebra of operators on a space X, then T is called a projection. To see why this name is appropriate, note that every x is mapped to the subspace TX of X, and all points in that subspace are left fixed by T (since T(Tx) = T2x = Tx). A projection is orthogonal if Tx is always orthogonal to x-Tx. This tells us that T is a projection on to some subspace Y of H, and that it takes each vector to the nearest point in Y, so that the vector x-Tx is orthogonal to the whole of the subspace Y.
 f (x)w(x)) is linear, and, provided w is small enough in some appropriate sense, M is a continuous linear map from X to X. Such maps are called multipliers. (Note that the property of “being a multiplier” depends not just on the space X and the map M but also on the way we choose to represent X as a space of functions, so it is not an intrinsic property of the map itself.)
f (x)w(x)) is linear, and, provided w is small enough in some appropriate sense, M is a continuous linear map from X to X. Such maps are called multipliers. (Note that the property of “being a multiplier” depends not just on the space X and the map M but also on the way we choose to represent X as a space of functions, so it is not an intrinsic property of the map itself.)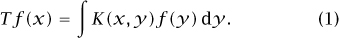
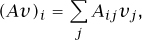
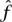 , which takes a function in L2 (
, which takes a function in L2 ( ) to another such function. It is defined by the formula
) to another such function. It is defined by the formula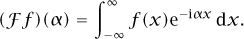
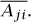 An n × n matrix A is unitary if AA* is the identity, orthogonal if A is real and AAT is the identity, Hermitian if A = A*, and self-adjoint if A = AT (in which case we say that A is symmetric). The operator T has one of these four properties if and only if its matrix A has the corresponding property.
An n × n matrix A is unitary if AA* is the identity, orthogonal if A is real and AAT is the identity, Hermitian if A = A*, and self-adjoint if A = AT (in which case we say that A is symmetric). The operator T has one of these four properties if and only if its matrix A has the corresponding property. from H to a Hilbert space H´ of functions that are square-integrable with respect to some MEASURE [III.55], and the map
from H to a Hilbert space H´ of functions that are square-integrable with respect to some MEASURE [III.55], and the map