 , with the 3 being a double root.
, with the 3 being a double root.Analogy is a powerful tool. When one can see parallels between two different theories, this often allows one to transport insights from one to the other. The idea of studying something “locally” comes from the theory of functions. Imported into number theory by way of an analogy between functions and numbers, it leads us to a whole new kind of number, the p-adic numbers, and to the local-global principle, which has become one of the guiding ideas of modern number theory.
Suppose that we have a polynomial such as
f(x) = -18 + 21x - 26x2 + 22x3 - 8x4 + x5.
From the very way the polynomial is written down, we can see certain things about it. For example, we can see at once that if we plug in x = 0, we get f(0) -18. Other things are less apparent. For example, to determine the values of f(2) or f(3), we would have to do some arithmetic. But if we were to rewrite the polynomial as
f(x) = 5(x - 2) - 6(x - 2)2 - 2(x - 2)3
+ 2(x - 2)4 + (x - 2)5,
we could see at once that f(2) = 0. (Of course, one needs to check that those two expressions really are equal!) Similarly, we can check that
f (x) = 10(x - 3)2 + 16(x - 3)3 + 7(x - 3)4 + (x - 3)5
and see at once that f(3) is also zero, and in fact that the polynomial has a double root at x = 3.
One way to think about this is to describe the first expression as “local at x = 0,” because it privileges the value 0 over all others. Then the other two expressions are local at 2 and local at 3, respectively. On the other hand, a formula like
f (x) = (x - 2)(x - 3)2(x2 + 1)
(which is also correct) is clearly more “global.” It tells us where all the roots are: at 2, 3, and ± , with the 3 being a double root.
, with the 3 being a double root.
The same ideas extend to functions that are not polynomials, as long as we allow the expressions to be infinite So, for example, let us take
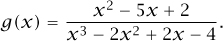
Locally at 0, we can write this as
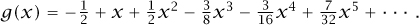
Or we can write it locally at 2:
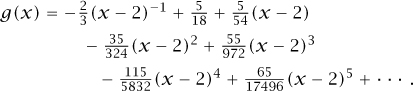
Notice that this time we had to use a negative power of (x -2), because plugging in x = 2 makes the denominator zero. Nevertheless, the expansion tells us that the “badness” at 2 is not too bad. Specifically, we can see that while g(2) is undefined, (x -2)g(2) makes sense and is equal to-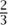
It is easy to keep going. To handle general functions locally at a, we may sometimes need to use fractional powers of (x - a), but it does not get much worse than that. Such expansions are a very powerful tool in the theory of functions. One of the motivations for the discovery of the p-adic numbers was to find a similarly powerful tool for the study of numbers.
It was DEDEKIND [VI.50] and Heinrich Weber who first realized that an analogy could be drawn between numbers and functions. In their scheme, positive whole numbers were compared to polynomials, while fractions were analogous to quotients of polynomials such as the function g(x) above. More complicated functions were like more complicated kinds of number. ELLIPTIC FUNCTIONS [V.31], for example, were similar to certain kinds of algebraic number. On the other hand, functions like sin(x) were more like TRANSCENDENTAL NUMBERS [III.41] such as e or π.
Dedekind and Weber pushed the idea that “functions are like numbers” in order to understand functions better. In particular, they showed that the techniques developed to study algebraic numbers could be used to study a whole class of functions, which came to be known as algebraic functions. It was Kurt Hensel, however, who saw that if functions are like numbers, then numbers must be like functions. In particular, he set out to find an analogue, for numbers, of the local expansions that were so useful in the theory of functions.
To get to Hensel’s idea, let us start by noticing that the way we usually represent numbers already points in the right direction. After all, an expression like 34 291 really means
34 291 = 1 + 9 · 10 + 2 · 102 + 4 · 103 + 3 · 104.
If we allow ourselves to think of 10 as being something like the variable x, this looks exactly like a polynomial. What is more, just as we can expand a polynomial in terms of different expressions (x - a), we can write numbers in other bases. For example,
34 291 = 4 + 4 · 11 + 8 · 112 + 3 · 113 + 2 · 114.
It is easy to see how to find this expansion. First, divide 34 291 by 11, and look at the remainder. It is 4. That is our first term. Next, subtract 4 from the original number to get something divisible by 11:
34 291 - 4 = 34 287 = 3117 · 11.
Now divide 3117 by 11 to find the next remainder, which will give the second term. Keep repeating this process, and you will find the base-11 expansion.
That sounds very promising, but there is one little insight missing. The fact is that 10 is not really like (x– 2), because 10 can be factored, while (x - 2) cannot. So expanding a number in base 10 is a little like trying to express a polynomial in powers of (x2 - 3x + 2), which factors as (x-1) (x-2). Such an expansion is not really local, since it is looking at two possible values of x at once. Similarly, the base-10 expansion mixes information about 2 and information about 5. The upshot is that we should always use a prime number as our base.
Just to fix ideas, let us choose p = 11. We already know that we can write positive numbers in base 11, i.e., as “polynomials in powers of 11.” What happens if we try it with a fraction? Let us take  . The first step is to find the remainder, that is, to find a number r (between 0 and 10) such that
. The first step is to find the remainder, that is, to find a number r (between 0 and 10) such that  - r is divisible by 11. Well,
- r is divisible by 11. Well,  - 6 = -
- 6 = -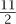 = -
= - · 11. So the first term is 6. (To see what is meant by divisibility here, consider what would have happened if we had taken r = 4. Then
· 11. So the first term is 6. (To see what is meant by divisibility here, consider what would have happened if we had taken r = 4. Then  - r would have been -
- r would have been - 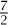 , and if we divide that by 11 we get -
, and if we divide that by 11 we get -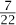 , which has a factor of 11 in the denominator. It is this that is not allowed and that does not happen when r = 6.)
, which has a factor of 11 in the denominator. It is this that is not allowed and that does not happen when r = 6.)
Now we repeat with the quotient, which was - . We see that -
. We see that - -5 = -
-5 = -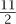 = -
= - . 11. So the second term will be 5 · 11. But now we find ourselves having to do -
. 11. So the second term will be 5 · 11. But now we find ourselves having to do - again! So we will do this again and again, and all of the remaining terms will have coefficient 5. In other words,
again! So we will do this again and again, and all of the remaining terms will have coefficient 5. In other words,
 = 6+5·11+5·112 +5·113 +5·114 +5·115 +·· · .
= 6+5·11+5·112 +5·113 +5·114 +5·115 +·· · .
It is not clear quite what the equals sign means here, but in any case we have obtained an infinite expansion in powers of 11. It is called the 11-adic expansion of  . Furthermore, the expansion “works” when we do arithmetic with it. For example, if we multiply it by 2 and do all the rearranging (2 × 6 = 12 = 1 + 11, so carry a 1, etc.) we do end up with 1.
. Furthermore, the expansion “works” when we do arithmetic with it. For example, if we multiply it by 2 and do all the rearranging (2 × 6 = 12 = 1 + 11, so carry a 1, etc.) we do end up with 1.
Hensel showed that one can do this with all algebraic numbers as long as one allows infinite expansions, a finite number of negative powers of 11 (so that one can handle 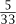 and similar things), and, in certain cases, fractional powers of 11. He argued that we should view such expansions as giving information “locally at 11.” The same happens with all of the prime numbers. So if we have a prime number p we can consider our numbers “locally at p” by taking their expansions in powers of p. These we call their p-adic expansions. Just as in the case of functions, such expansions immediately tell us how divisible by p a number is, while hiding all the information about other primes; in that sense, they are truly “local.”
and similar things), and, in certain cases, fractional powers of 11. He argued that we should view such expansions as giving information “locally at 11.” The same happens with all of the prime numbers. So if we have a prime number p we can consider our numbers “locally at p” by taking their expansions in powers of p. These we call their p-adic expansions. Just as in the case of functions, such expansions immediately tell us how divisible by p a number is, while hiding all the information about other primes; in that sense, they are truly “local.”
The best answers always raise new questions. Having discovered that any rational number has a p-adic expansion, and that one can “do arithmetic” directly with the expansions, it is inevitable to ask whether we have therefore enlarged the world of numbers under consideration. Once we have chosen the prime p, any rational number gives us a p-adic expansion. But does every such expansion come from a rational number?
Not a chance. It is easy to see that the set of all expansions is much bigger than the set of all rational numbers. Hensel’s next move, then, was to point out that the set ℚp of all possible p-adic expansions is a new realm of numbers, which he called the p-adic numbers. It includes not only all the rational numbers, but also a lot more.
The best way to think of ℚp is by analogy with the set ℝ of all real numbers. Real numbers are usually given by their decimal expansions. When we write e = 2.718 . . . , what we mean is that
e = 2 + 7 · 10-1 + 1 · 10-2 + 8 · 10-3 + ··· .
The set of all such expansions is the set of all real numbers. It contains all the rational numbers, but is much bigger.
Of course, except for the fact that both contain the rationals, these two realms are almost completely different. For example, in both ℚp and ℝ there is a natural notion of “distance between two numbers.” But these distances are completely different, even when the numbers in question are rational. So, in the reals, 2 is very close to 2001/1000. In the 5-adics, however, the distance between these two numbers is quite large!
It turns out that we can do calculus with p-adic numbers, just as we do it with reals. Many other mathematical ideas also extend. So Hensel’s ideas led to a system of “parallel (numerical) universes”—one for each prime, plus the real numbers—in which we can do mathematics.
At first, most mathematicians seem to have found Hensel’s new numbers interesting in a formal way, but also to have wondered what the point of them was. One does not adopt a new number system just for fun; it needs to be useful for something. Hensel was fascinated by his numbers and kept writing about them, but to begin with he had trouble demonstrating their usefulness. He showed, for example, that they could be used to develop the basics of algebraic number theory in a new way—but most folks seemed happy with the old way.
One can demonstrate the power of a new idea by giving a beautiful and easy proof of a difficult result. Hensel wrote a paper purporting to do just that: he gave an easy and elegant p-adic proof that the number e is transcendental. This did get people’s attention. Unfortunately, when they looked hard at the proof they realized that it contained a subtle error. As a result, mathematicians’ attitude of suspicion about Hensel’s strange new numbers was reinforced.
The tide was turned by Helmut Hasse. He had been studying in Göttingen. At one point, he walked into a used bookstore and found a copy of Hensel (1913), a book written a few years earlier. Hasse was fascinated, and moved to Marburg to study with Hensel. A couple of years later, in 1920, he found the idea that was to make the p-adic numbers a crucial tool for number theorists.
What Hasse showed was that it was possible to answer some questions in number theory by answering them “locally.” Here is a (not very important, but fairly easy to follow) example. Suppose x is a rational number that is a square of some other rational number y, so x = y2. Since all rational numbers are also p-adic, it is true that for every prime number p the number x, thought of as a p-adic number, is a square. And similarly, the real number x is a square. In other words, the rational number y is a kind of “global” square root, in that it serves as a square root in each local setting.
So far, so boring. But now reverse the thing. Suppose that we know that or every prime number p the number x, thought of as a p-adic number, is the square of some p-adic number (which may depend on p), and also that x, thought of as a real number, is the square of some real number. A priori, these local square roots of x could all be different! But it turns out that under these assumptions x must be the square of some rational number, so that in fact all the local roots must come from a “global” root.
This leads us to think of the rational numbers as “global” and of the various ℚp and of ℝ as “local.” Then the previous paragraph claims that the property of “being a square” is true globally if and only if it is true “everywhere locally.” This turns out to be a powerful and illuminating idea, and it has become known as the Hasse principle or the local-global principle.
Our example, of course, demonstrates the principle in its strongest case: solve a problem locally in all cases, and you have solved it globally. That is often too much to hope for. Nevertheless, attacking a problem locally and then putting the local pieces together has become a fundamental technique in modern number theory. It has been used to simplify older proofs, as in CLASS FIELD THEORY [V.28], and also to obtain new results, as in Wiles’s proof of FERMAT’S LAST THEOREM [V.10]. So Hensel was right after all: his new numbers have earned their place along with the real numbers in every number theorist’s heart.
Gοuvêa, F. Q. 2003. p-adic Numbers: An Introduction, revised 3rd printing of the 2nd edn. New York: Springer.
Hasse, H. 1962. Kurt Hensels entscheidener Anstoss zur Entdeckung des Lokal-Global-Prinzips Journal für die reine und angewandte Mathematik 209:3-4.
Hensel, K. 1913. Zahlentheorie. Leipzig: G. J. Göschenische.
Roquette, P. 2002. History of valuation theory. I. In Valuation Theory and Its Applications, volume I, pp. 291-355. Providence, RI: American Mathematical Society.
Ullrich, P. 1995. On the origins of p-adic analysis. Proceedings of the 2nd Gauss Symposium. Conference A: Mathematics and Theoretical Physics, Munich, 1993, pp. 459-73. Symposia Gaussiana. Berlin: Walter de Gruyter.
Ullrich, P. 1998. The genesis of Hensel’s  -adic numbers. In Charlemagne and His Heritage. 1200 Years of Civilization and Science in Europe, volume 2, pp. 163-78. Turnhout: Brepols.
-adic numbers. In Charlemagne and His Heritage. 1200 Years of Civilization and Science in Europe, volume 2, pp. 163-78. Turnhout: Brepols.