
There are many contexts in mathematics, especially in analysis, where one would like to say that two mathematical objects are close, and understand precisely what that means. If the two objects are the points (x1, x2) and (y1, y2) in a plane, then the task is straightforward: the distance between them is

by the Pythagorean theorem, and it makes sense to say that the points are close if this distance is small.
Now suppose that we have two points in n-dimensional space, (x1, . . . ,xn) and (y1, . . . ,yn). It is a simple matter to generalize the formula just given when n = 2 and define the distance between them to be
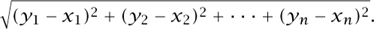
Of course, the fact that the formula can be easily generalized is not in itself a guarantee that the resulting notion is a sensible definition of distance. And this raises the question of what properties we would like a definition to have for it to count as sensible. A metric space is an abstract notion that results from thinking about this question.
Let X be a set of “points.” Suppose that, given any two of these points, x and y say, we have a way of assigning a real number d(x,y) that we wish to regard as the distance between them. The following three properties are ones that it would be highly desirable for this idea of distance to have.
(P1) d(x,y) ≥ 0 with equality if and only if x = y.
(P2) d(x,y) = d(y, x) for any two points x and y.
(P3) d(x,y) + d(y, z) ≥ d(x, z) for any three points x, y, and z.
The first of these properties says that the distance between two points is always positive, except when the two points are the same, when it is zero. The second says that distance is a symmetric notion: the distance from x to y is the same as the distance from y to x. The third is called the triangle inequality if you imagine x, y, and z as the vertices of a triangle, it says that the length of any side never exceeds the sum of the lengths of the other two sides.
A function d defined on pairs of points (x,y) from a set X is called a metric if it has properties (P1)-(P3) above. In that case, X and d together form a metric space. This abstraction of the usual notion of distance is very useful, and there are many important examples of metrics that are not necessarily derived from the Pythagorean theorem. Here are a few examples.
(i) Let X be n-dimensional space, that is, the set ℝn of all sequences (x1, . . . , xn) of n real numbers. It can be shown that the formula derived above from the Pythagorean theorem gives a notion of distance that does indeed satisfy properties (P1)-(P3). This metric is called the Euclidean distance and the resulting metric space is called Euclidean space. Euclidean spaces are perhaps the single most basic and important class of metric spaces in mathematics.
(ii) Nowadays, information is often transmitted digitally in the form of a string of 0s and 1s, such as 000111010010. The Hamming distance between two such strings is defined to be the number of places where the strings are different. For example, the Hamming distance between the strings 00110100 and 00100101 is 2, since the strings differ in the fourth and eighth places only. This idea of distance also satisfies properties (P1)-(P3).
(iii) If you are driving from one town to another, then the distance you care about is not the distance as the crow flies but the length of the shortest route along the network of available roads. Similarly, if you wish to travel from London to Sydney, then what matters is the length of the shortest path (known as a geodesic) along the Earth’s surface, rather than the “actual” distance through the Earth itself. Many useful metrics come from this general idea of a shortest route, which guarantees that property (P3) will hold.
(iv) An important feature of Euclidean distance is its rotational symmetry: in other words, rotating the plane, or space, does not alter the Euclidean distances between points. There are other metrics that also have a great deal of symmetry, and these have great geometrical significance. In particular, the discovery of the HYPERBOLIC METRIC [I.3 §§6.6, 6.10] in the early nineteenth century demonstrated that the parallel postulate could not be proved using Euclid’s other axioms. This resolved a question that had been open for thousands of years. See RIEMANNIAN METRICS [I.3 §6.10].