 we have the very useful cancelation law: if ac ≡ bc mod
we have the very useful cancelation law: if ac ≡ bc mod  and c
and c 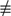 mod
mod  , then a ≡ b mod
, then a ≡ b mod  .
.Is there a square number whose decimal expansion ends . . . 7? Is 438 345 divisible by 9? For which positive integers n is n2 - 5 a power of two? Is n7 - 77 ever a Fibonacci number?
These questions, and more, can be answered using modular arithmetic. Let us look at the first question. Listing the first few squares, 1, 4, 9, 16, . . . , one does not find any whose final digit is 7. In fact, writing down just the final digits, one gets the sequence
1, 4, 9, 6, 5, 6, 9, 4, 1, 0, 1, 4, 9, 6, 5, 6, . . . ,
which seems to repeat (and thus never contain the number 7).
An explanation of this phenomenon is as follows. Let n be a number to be squared. We can always write n as a multiple of 10 plus a remainder; that is, n = 10q + r, where r ∈ {0, 1, . . . , 9}. Now, if we square n we get
n2 = (10q + r)2
= 100q2 + 20qr + r2
= 10(10q2 + 2qr) + r2.
The only part of this expression that affects the final digit is the r2, which immediately explains why the sequence of last digits of squares repeats with period 10, and hence contains no 7s.
Modular arithmetic is essentially just a notation for writing down arguments of this sort. If two numbers (like n and r) leave the same remainder on division by 10, then we say that they are congruent modulo 10 and write n ≡ r mod 10. What we proved above is the statement that, if n ≡ r mod 10, then n2 ≡ r2 mod 10.
Everything we have just said applies equally well if we replace 10 by an arbitrary modulus m: if n and r leave the same remainder on division by m, then we say that n and r are congruent modulo m and we write n ≡ r mod m. Equivalently, n and r are congruent modulo m if m divides n - r. (An integer a is said to divide another integer b if b is an integer multiple of a.) The above argument is just one instance of the following general fact, which is not hard to prove: if a ≡ a' mod m and b ≡ b' mod m, then ab ≡ a'b' mod m and a + b ≡ a' + b' mod m.
Now observe that 10 = 1 mod 9. It follows that 10 × 10 = 1 × 1 = 1 mod 9, and in fact that 10d = 1 mod 9 for any d ∈ ℕ. Suppose that we have a number N whose decimal expansion is adad-1 ··· a2a1a0. This means that
N = adl0d + ad-110d-1 + ··· + a1l0 + a0.
Applying the rules of modular arithmetic, we get
N ≡ ad + ad-1 + ··· + a1 + a0 mod 9.
This gives the well-known test for divisibility by 9: simply add up the digits of the number in base 10, and see if the result is divisible by 9. For the example N = 438 345 the sum of the digits is 27, which is divisible by 9. So N is a multiple of 9 (in fact N = 9 × 48 705).
If m is a modulus and n is an integer, then there is precisely one value of r between 0 and m - 1 such that n ≡ r mod m. This number r is often called the least residue or simply the residue of n to the modulus m.
Now let us consider the third question posed at the beginning of this article, namely the matter of when n2 - 5 is a power of two. When n = 3, 32 - 5 = 4 is a power of two, but a little experimentation does not reveal any further examples. What aspect of the problem changes as n becomes larger than 3? The key observation is that n2 - 5 is now greater than 4, and so if it were a power of 2, then it would have to be divisible by 8. That would mean that n2 ≡ 5 mod 8, but this is never the case. Indeed, the residues of the first eight squares are 1, 4, 1, 0, 1, 4, 1, 0, and we know that the sequence will repeat with period 8 (actually, it repeats with period 4). Thus, it never contains a 5.
Modular arithmetic should be used with care. Although the rules for addition and subtraction are simple, division is somewhat more subtle. For example, if we are given that ac ≡ bc mod m, it is not, in general, permissible to divide by c and conclude that a ≡ b mod m: consider, for instance, the case a = 2, b = 4, c = 3, m = 6.
Let us examine what has just gone wrong. To say that ac ≡ bc mod m means that m divides ac - bc = (a-b)×c. But this clearly does not mean that m divides a - b, since m could divide c (or at least have a common factor with it). However, if m has no factor in common with c, then it must divide a - b, so in this case we do indeed have a ≡ b mod m. In particular, for any prime number  we have the very useful cancelation law: if ac ≡ bc mod
we have the very useful cancelation law: if ac ≡ bc mod  and c
and c 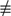 mod
mod  , then a ≡ b mod
, then a ≡ b mod  .
.
The examples so far may have suggested that the principal uses of modular arithmetic are to do with specific moduli such as 10 and 8. However, this is far from true, and the subject really comes into its own when one looks at more general m. For example, one of the basic results in number theory is Fermut’s little theorem, which states that if  is a prime and a
is a prime and a 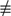 0 mod
0 mod  , then a
, then a -1 ≡ 1 mod
-1 ≡ 1 mod  . Let us quickly prove this. Consider the numbers a, 2a, 3a, . . . , (
. Let us quickly prove this. Consider the numbers a, 2a, 3a, . . . , ( - 1) a mod
- 1) a mod  . If ra ≡ sa mod
. If ra ≡ sa mod  , then from the cancelation law we can deduce that r ≡ s mod
, then from the cancelation law we can deduce that r ≡ s mod  , from which it follows that a, 2a, . . . , (
, from which it follows that a, 2a, . . . , ( - 1)a are all different modulo
- 1)a are all different modulo  . Furthermore, none of these numbers is 0 mod
. Furthermore, none of these numbers is 0 mod  . We are thus forced to conclude that the numbers a, 2a, 3a, . . . , (
. We are thus forced to conclude that the numbers a, 2a, 3a, . . . , ( - 1)a mod
- 1)a mod  are simply a rearrangement of the numbers 1, 2, 3, . . . ,
are simply a rearrangement of the numbers 1, 2, 3, . . . ,  - 1 mod
- 1 mod  . In particular, the products of the numbers in these two sets are the same, which implies that
. In particular, the products of the numbers in these two sets are the same, which implies that
a -1(
-1( - 1)! ≡ (
- 1)! ≡ ( - 1)! mod
- 1)! mod  .
.
Since ( - 1)! is not a multiple of
- 1)! is not a multiple of  , we can apply the cancelation law again and divide both sides by (
, we can apply the cancelation law again and divide both sides by ( - 1)!. This implies the result.
- 1)!. This implies the result.
Euler’s theorem is a generalization of Fermat’s little theorem to composite moduli. It states that if m is a positive integer and a is another positive integer that is coprime to m (this means that a and m have no common factor), then aϕ(m) ≡ 1 mod m. Here ϕ is Euler’s totient function: ϕ(m) is the number of integers less than m that are coprime to m. For instance, if m = 9, then the integers less than m and coprime to m are 1, 2, 4, 5, 7, and 8, so ϕ(9) = 6 and we can deduce from Euler’s theorem that 56 ≡ 1 mod 9. Let us check this directly: 56 = 15 625, so the sum of its digits is 19, which is indeed congruent to 1 mod 9. For further discussion of the Fermat-Euler theorem, see MATHEMATICS AND CRYPTOGRAPHY [V11.7], COMPUTATIONAL NUMBER THEORY [IV.3], and THE WEIL CONJECTURES [V.35].
The final question from above—whether n7 - 77 is ever a Fibonacci number—is left as an exercise to the reader.