When one first learns about the complex numbers, one is taught to think of them as a two-dimensional space, with one real and one imaginary dimension: a complex number z = x + iy has real part x and imaginary part y, where i is a square root of - 1.
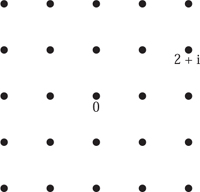
Now let us consider what the complex numbers that have integers for their real and imaginary parts look like. These complex numbers, such as 3 + 4i or -23i, form a “lattice” in the complex plane (see figure 1).
By definition, every element of this lattice is of the form m + ni for some pair of integers m and n. We say that the lattice is generated by 1 and i, and use the notation ℤ + ℤi for it. Note that this lattice can be generated in plenty of other ways. For example, it is also generated by the pair (1, -i), the pair (1, 100+i) or even the pair (101 + i, 100 + i). In fact, one can easily check that this lattice is generated by the pair (a + bi, c + di) (meaning that every element of the lattice is an integer combination of a + bi and c + di) if and only if a, b, c, and d are integers and ad - bc = ±1.
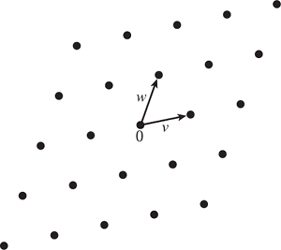
Now let v and w be any two complex numbers and consider the set of complex numbers of the form av + bw, again with a and b integers (see figure 2).
A lattice is exactly such a thing: a grid ℤv + ℤw in the complex plane generated by two complex numbers v and w, with the provisos that neither v nor w is zero and that v/w is not real (this is just to ensure that v and w do not both lie on one line).
If τ = x + iy is a complex number with y ≠ 0, then there is a standard lattice associated with τ, namely ℤτ+ℤ. We call this lattice Λτ and note that Λτ = Λ-τ. In general, however, distinct complex numbers τ give rise to distinct lattices—and furthermore there are plenty of lattices that are not equal to Λτ for any τ, for the simple reason that 1 belongs to Λτ for every τ.
If Λ is a lattice generated by v and w, and α is a nonzero complex number, then one can multiply the entire situation by α and deduce that αΛ is the lattice generated by αΛ and αw. Geometrically, this says that one can rotate and rescale lattices.
If Λ is a lattice generated by v and w, and we scale it by dividing everything by w, then we get a new lattice (1/w)Λ, which is generated by v/w and w/w = 1. In particular, this new lattice is equal to Λτ for the complex number τ = v/w.
It may seem like an odd thing to do, but one can apply this scaling trick to Λτ itself. The lattice Λτ is generated by (τ, 1) but also by any pair (v, w) = (aτ + b, cτ + d), if a, b, c, and d are integers such that ad - bc = ±1. If we divide by cτ + d and set σ = (aτ + b)/(cτ + d), then we see that

The formal definition of a modular form is rather unenlightening: it is a function that obeys certain boundedness conditions and transformation properties. One way of seeing where the transformation properties come from is to think about lattices. If k is an integer, then a modular form of weight k is a function f that associates a complex number f(Λ) with any lattice Λ, and has the property that
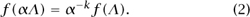
The function also has to satisfy some other properties (a differentiability condition and a boundedness condition), but the crucial property is the one above. If k is even and at least 4, then an example of a modular form of weight k is the Eisenstein series Gk defined by the formula
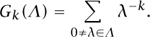
The assumption that k is at least 4 guarantees that the sum converges, and the evenness of k ensures that the function is nonzero.
We have seen that any lattice can be scaled so that it takes the form Λτ for some τ, so (2) implies that a modular form will be determined by its values on such lattices. If 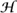 denotes the complex numbers with positive imaginary part, then, because Λτ = Λ-τ, a modular form is in fact determined by its values on Λτ for τ ∈
denotes the complex numbers with positive imaginary part, then, because Λτ = Λ-τ, a modular form is in fact determined by its values on Λτ for τ ∈ 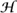 .
.
However, an arbitrary function on 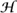 does not give us a modular form: equation (1) tells us that if f is a modular form and F is the function on
does not give us a modular form: equation (1) tells us that if f is a modular form and F is the function on 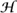 defined by F(τ) = f(Λτ), then F must satisfy the equation
defined by F(τ) = f(Λτ), then F must satisfy the equation
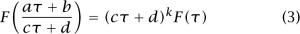
for every a, b, c, d ∈ ℤ such that ad - bc = 1. (The reason we exclude the case ad - bc = -1 is that (aτ + b)/(cτ + d) would not be in the upper half-plane in this case.) This is the equation at the heart of the definition of a modular form.
Over the years, mathematicians have isolated other desirable properties that F should have in order to give a useful theory. Nowadays, modular forms are required to obey the additional properties that F is HOLOMORPHIC [I.3 §5.6] and that F(x + iy) does not grow too quickly as y goes to + ∞; these assumptions imply that the vector space of weight k modular forms is finite dimensional. The Eisenstein series above do have these additional properties, and are the first basic examples of modular forms.
Modular forms have connections with arithmetic, geometry, representation theory, and even physics. Modular forms also played a key role in the Taylor–Wiles proof of FERMAT’S LAST THEOREM [V.10]. Why is this? One general reason is that there are links between modular forms and other mathematical objects: here we briefly explain one of the links.
Lattices in the complex plane are related to ELLIPTIC CURVES [III.21]: the quotient of the complex numbers by a lattice is an elliptic curve, and every elliptic curve arises in this way. Hence to study elliptic curves, or families of elliptic curves, one can instead study families of lattices. One way of studying an object is by studying the functions on that object, and a modular form is precisely that: a function on the collection of all lattices. And indeed, automorphic forms, which are generalizations of modular forms, have been used to great effect in studying a wide variety of families of algebraic objects in this way.