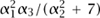 .) Then it turns out that K is a number field (the one thing that is not completely obvious is that it has finite degree over ℚ), which we denote by ℚ(α1, . . . , αk). Conversely, every number field is of this form.
.) Then it turns out that K is a number field (the one thing that is not completely obvious is that it has finite degree over ℚ), which we denote by ℚ(α1, . . . , αk). Conversely, every number field is of this form.A number field K is a “finite-degree field extension” of ℚ, the field of rational numbers. This means that K is a FIELD [I.3 §2.2] that is finite dimensional when one regards it as a VECTOR SPACE [I.3 §2.3] over ℚ. The following alternative description is somewhat more concrete. Take finitely many algebraic numbers αl, . . . , αk (that is, roots of polynomials with integer coefficients) and consider the field K of all rational functions in the αi. (In other words, K consists of numbers like 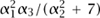 .) Then it turns out that K is a number field (the one thing that is not completely obvious is that it has finite degree over ℚ), which we denote by ℚ(α1, . . . , αk). Conversely, every number field is of this form.
.) Then it turns out that K is a number field (the one thing that is not completely obvious is that it has finite degree over ℚ), which we denote by ℚ(α1, . . . , αk). Conversely, every number field is of this form.
The simplest number fields are perhaps the quadratic fields. These are fields of the form ℚ(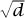 ) = {a + b
) = {a + b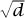 : a, b ∈ ℚ}, where d is an integer (which, it is important to stress, may be negative) that is squarefree. This last condition tells us that d has no nontrivial square factors. It is there for convenience so that all the ℚ(
: a, b ∈ ℚ}, where d is an integer (which, it is important to stress, may be negative) that is squarefree. This last condition tells us that d has no nontrivial square factors. It is there for convenience so that all the ℚ(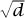 ) will be distinct. (For example, ℚ(
) will be distinct. (For example, ℚ(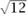 ), if we were to allow it, would equal ℚ(
), if we were to allow it, would equal ℚ(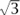 ), since
), since 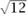 = 2
= 2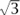 .) Among the other important number fields are the cyclotomic fields. Here we take a primitive mth root of unity ζm (which, for concreteness, one could take to be e2πi/m) and “adjoin” it to ℚ, obtaining the field ℚ(ζm).
.) Among the other important number fields are the cyclotomic fields. Here we take a primitive mth root of unity ζm (which, for concreteness, one could take to be e2πi/m) and “adjoin” it to ℚ, obtaining the field ℚ(ζm).
Why consider number fields? Historically, an important reason is that they allow us to factorize certain Diophantine equations. For example, the Ramanujan–Nagell equation x2 = 2n - 7 may be factorized as
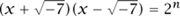
if we allow coefficients in the field 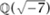 , while the Fermat equation xn + yn = zn is equivalent to
, while the Fermat equation xn + yn = zn is equivalent to
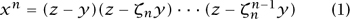
if we allow coefficients in the field ℚ(ζn).
Before one can start thinking about whether such factorizations are useful, it is necessary to understand the notion of an integer in a number field K. A number α ∈ K is an (algebraic) integer if it is a root of a monic polynomial with coefficients in ℤ: that is, a polynomial with leading coefficient 1. For simple fields like ℚ(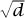 ) with d squarefree, the integers can be described quite explicitly. They are all the numbers of the form a + b
) with d squarefree, the integers can be described quite explicitly. They are all the numbers of the form a + b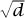 for integers a and b, unless d ≡ 1 (mod 4), in which case we must include more numbers: we get all numbers of the form a + b(
for integers a and b, unless d ≡ 1 (mod 4), in which case we must include more numbers: we get all numbers of the form a + b( (1 +
(1 + 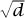 )), again for integers a and b. The set of integers in K is often denoted by (
)), again for integers a and b. The set of integers in K is often denoted by ( K, and it forms a RING [III.81 §1].
K, and it forms a RING [III.81 §1].
Unfortunately, factorizations such as (1) are not as helpful as they seem at first sight: 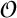 K turns out not to be OK, at least if one expects familiar properties of the ring ℤ to carry over unchanged. In particular, unique factorization into primes fails to hold: for example, 2 · 3 = (1 +
K turns out not to be OK, at least if one expects familiar properties of the ring ℤ to carry over unchanged. In particular, unique factorization into primes fails to hold: for example, 2 · 3 = (1 + 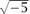 ) (1 -
) (1 - 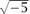 ) in the field ℚ(
) in the field ℚ(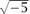 ). The numbers on both sides are integers in this field, and it is not possible to decompose any of them any further.
). The numbers on both sides are integers in this field, and it is not possible to decompose any of them any further.
Amazingly, unique factorization may be restored by embedding  K into a larger set, which consists of objects called IDEALS [III.81 §2]. There is a natural EQUIVALENCE RELATION [I.2 §2.3] that one can place on these ideals, and the number of equivalence classes, called the class number and written h(K), is one of the most important invariants in number theory: in a certain sense, it measures “the extent to which unique factorization fails” in the number field K. (See ALGEBRAIC NUMBERS [IV.1 §7] for more details.) The fact that it is finite is one of the two basic finiteness theorems in algebraic number theory.
K into a larger set, which consists of objects called IDEALS [III.81 §2]. There is a natural EQUIVALENCE RELATION [I.2 §2.3] that one can place on these ideals, and the number of equivalence classes, called the class number and written h(K), is one of the most important invariants in number theory: in a certain sense, it measures “the extent to which unique factorization fails” in the number field K. (See ALGEBRAIC NUMBERS [IV.1 §7] for more details.) The fact that it is finite is one of the two basic finiteness theorems in algebraic number theory.
When h(K) = 1, the integers  K themselves enjoy unique factorization, without the need for extra ideals. This does not happen particularly often; among the fields ℚ(
K themselves enjoy unique factorization, without the need for extra ideals. This does not happen particularly often; among the fields ℚ(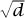 ) with d positive and squarefree, only nine have this property, namely d = 1, 2, 3, 7, 11, 19, 43, 67, and 163. The problem of determining these numbers was posed by GAUSS [VI.26] and finally solved by Heegner in 1952.
) with d positive and squarefree, only nine have this property, namely d = 1, 2, 3, 7, 11, 19, 43, 67, and 163. The problem of determining these numbers was posed by GAUSS [VI.26] and finally solved by Heegner in 1952.
The fact that 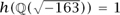 is closely related to some remarkable facts. For example, the polynomial x2 + x + 41 takes prime values when x = 0, 1, . . . , 39 (observe that 4 × 41 = 163 + 1), and the number
is closely related to some remarkable facts. For example, the polynomial x2 + x + 41 takes prime values when x = 0, 1, . . . , 39 (observe that 4 × 41 = 163 + 1), and the number 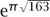 is within 10-12 of an integer.
is within 10-12 of an integer.
It is a well-known open problem to decide whether or not there are infinitely many fields ℚ(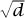 ), d > 0, with class number 1. Gauss and many subsequent authors have conjectured that there are.
), d > 0, with class number 1. Gauss and many subsequent authors have conjectured that there are.
The second basic finiteness result in algebraic number theory is Dirichlet’s unit theorem. A unit is simply some x ∈  K such that there exists y ∈
K such that there exists y ∈  K with xy = 1. The numbers 1 and -1 are always units, but there can certainly be others: for example, 17 - 12
K with xy = 1. The numbers 1 and -1 are always units, but there can certainly be others: for example, 17 - 12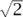 is a unit in ℚ(
is a unit in ℚ(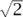 ) (since its reciprocal is 17 + 12
) (since its reciprocal is 17 + 12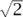 ). The units form an Abelian group
). The units form an Abelian group 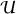 K under multiplication. Dirichlet’s theorem states that this group has finite rank, which means that it is generated by finitely many of its elements.
K under multiplication. Dirichlet’s theorem states that this group has finite rank, which means that it is generated by finitely many of its elements.
If d > 0 is squarefree and if K = ℚ(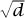 ), then
), then 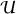 K has rank 1. When d
K has rank 1. When d 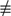 1 (mod 4), the fact that it has rank at least 1 is equivalent to the statement that the Pell equation x2 - dy2 = 1 always has a nontrivial solution. This is because the Pell equation factors as (x - y
1 (mod 4), the fact that it has rank at least 1 is equivalent to the statement that the Pell equation x2 - dy2 = 1 always has a nontrivial solution. This is because the Pell equation factors as (x - y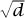 ) (x + y
) (x + y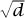 ) = 1. The unit 17 - 12
) = 1. The unit 17 - 12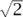 in ℚ(
in ℚ(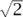 ) corresponds to the solution x = 17, y = 12 of the equation x2 - 2y2 = 1.
) corresponds to the solution x = 17, y = 12 of the equation x2 - 2y2 = 1.
For more about some of the topics discussed in this article, see FERMAT’S LAST THEOREM [V.10].