 in the reals is well-ordered, while the set
in the reals is well-ordered, while the set 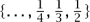 is not. The first set is order isomorphic to the ordinals less than ω + ω, meaning that there is a bijection that preserves the order. So one says that that set has order type ω + ω.
is not. The first set is order isomorphic to the ordinals less than ω + ω, meaning that there is a bijection that preserves the order. So one says that that set has order type ω + ω.Loosely speaking, the ordinals are what we get if, starting with 0, we use the following two procedures. We can add 1 to whatever we have, and we can “collect together” (or “take the limit of”) whatever we have so far. So from 0 we would get 1, then 2, then 3, and so on. After all of those, we could take their “limit” (i.e., the limit of 0, 1, 2, 3, . . .), which is called ω. Then we can add 1, obtaining ω + 1, then ω + 2, and so on. And then we can take the limit of all of those, to obtain an ordinal we could write as ω + ω. And so on. Note that this final “and so on” carries quite a lot inside it. For example, the ordinals do not just consist of finite sums of ws and natural numbers, since we can take the limit of ω, ω + ω, ω + ω + ω, . . . , which we might call ω2.
Ordinals arise in two ways (which turn out to be closely related). First, they give a measure of the “size” of a well-ordering. A well-ordering on a set is an ordering in which every (nonempty) subset has a least element. For example, the set  in the reals is well-ordered, while the set
in the reals is well-ordered, while the set 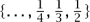 is not. The first set is order isomorphic to the ordinals less than ω + ω, meaning that there is a bijection that preserves the order. So one says that that set has order type ω + ω.
is not. The first set is order isomorphic to the ordinals less than ω + ω, meaning that there is a bijection that preserves the order. So one says that that set has order type ω + ω.
Ordinals also commonly arise when one wishes to index transfinite processes. Here “transfinite” means “going beyond finite.” As an example, suppose that we wish to “count, in increasing order” the elements of the well-ordered set above. How would we do it? We would start with  , then
, then 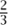 , then
, then 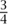 , and so on. But, at the end of all time, we would still not have reached elements like or
, and so on. But, at the end of all time, we would still not have reached elements like or 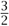 or
or 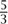 . So we would start again: “at time ω” we would count
. So we would start again: “at time ω” we would count 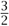 , then at time ω + 1 we would count
, then at time ω + 1 we would count 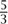 , and so on. Thus our counting is complete by time ω + ω.
, and so on. Thus our counting is complete by time ω + ω.
For a more detailed explanation of ordinals, including more examples and more on how they arise in mathematics, see SET THEORY [IV.22 §2].