III.70 π
What makes one number more fundamental and important, mathematically speaking, than another? Why, for instance, would almost everybody agree that 2 is more important than 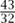 ? One possible answer is that what really matters about a number is its properties, and in particular any interesting properties it might have that distinguish it from all other numbers. Of course, we now have to decide what counts as an interesting property: for example, why do we not regard it as interesting that
? One possible answer is that what really matters about a number is its properties, and in particular any interesting properties it might have that distinguish it from all other numbers. Of course, we now have to decide what counts as an interesting property: for example, why do we not regard it as interesting that 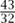 is the only number that gives you
is the only number that gives you 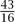 when you double it? An obvious reason is that there is an analogous property for every number x you might care to choose: x is the only number that gives you 2x when you double it. By contrast, the property “is the smallest prime number” does not mention any specific number and is easily stated in terms of a concept, that of “prime number,” whose importance is itself easy to explain. This property must apply to exactly one number, so it is likely that that number will have an important part to play in mathematics, and indeed it does. (As it happens,
when you double it? An obvious reason is that there is an analogous property for every number x you might care to choose: x is the only number that gives you 2x when you double it. By contrast, the property “is the smallest prime number” does not mention any specific number and is easily stated in terms of a concept, that of “prime number,” whose importance is itself easy to explain. This property must apply to exactly one number, so it is likely that that number will have an important part to play in mathematics, and indeed it does. (As it happens, 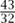 conjectured to be an important critical exponent in statistical physics, which means that it can be singled out as an interesting number, though still nothing like as fundamental as 2.)
conjectured to be an important critical exponent in statistical physics, which means that it can be singled out as an interesting number, though still nothing like as fundamental as 2.)
Everybody agrees that π is one of the most important numbers in mathematics, and it is easy to justify this assessment by the criterion of the previous paragraph, because π has an abundance of properties—so many that when π appears unexpectedly in a calculation, one is not unduly surprised. For example, the following is a famous theorem of EULER [VI.19]:
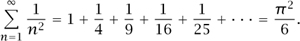
What on earth, one might wonder, has π to do with adding up reciprocals of squares? This is a perfectly legitimate question, but the idea that there could in principle be a connection is not, to an experienced mathematician, a surprise. A very common way to prove mathematical identities is to show that the two sides of the identity are different ways of evaluating the same quantity. In this case, one can use a basic fact from FOURIER ANALYSIS [III.27], known as Plancherel′s identity, which states the following. If f : ℝ → ℂ is a periodic function with period 2π, and for every integer n (positive or negative) we define its nth Fourier coefficient en by the formula
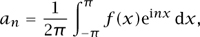
then
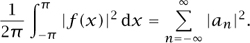
If you now take as f the function that is 1 whenever x is between (2n -  )π and (2n +
)π and (2n +  )π for some integer n, and 0 otherwise, then you find that the left-hand side works out as
)π for some integer n, and 0 otherwise, then you find that the left-hand side works out as  . You also find, after a small calculation, that |an|2 = 1/(πn)2 when n is odd, that |a0|2 =
. You also find, after a small calculation, that |an|2 = 1/(πn)2 when n is odd, that |a0|2 = 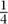 , and that |an|2 = 0 whenever n is even and nonzero. Therefore,
, and that |an|2 = 0 whenever n is even and nonzero. Therefore,
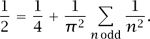
Bearing in mind that n2 = (-n)2, we can deduce easily that
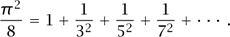
This closely resembles the identity we were trying to prove, which we can get by noticing that the right-hand side is equal to Σn 1/n2 - Σn 1/(2n)2, which is three quarters of Σn 1/n2. Therefore, Σn 1/n2 = π2/6.
Now we have a reason for the appearance of π: it comes up in the formula for the Fourier coefficients. What is more, its appearance there can be explained as well. A periodic function on ℝ is more naturally thought of as a function defined on the unit circle. The Fourier coefficient an is a certain average defined on the unit circle, so we have to divide by the length of the circle, which is 2π
What, then, is π? Well, we have just seen what is perhaps the most elementary definition: it is the ratio of the circumference of a circle to its diameter. But what makes π so interesting is that it has many different defining properties. Here are a few more of them.
(i) Define a function sin x to be equal to the sum of the power series
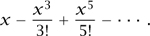
Then π is the smallest positive number x such that sin x = 0. (For more on sin x, see TRIGONOMETRIC FUNCTIONS [III.92].)
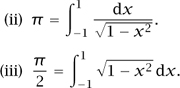
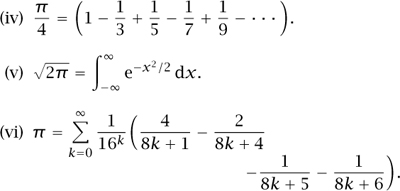
The integrals on the right-hand sides of the second and third properties above are expressions for half the circumference of the unit circle and half its area, respectively. So those definitions are analytical expressions of the geometrical facts that a unit circle has circumference 2π and area π, respectively.
The fifth property tells us what constant to put in front of 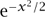 to make it into the famous NORMAL DISTRIBUTION [III.71 §5]. (Why should π come into it? One can give several reasons. One is that the function
to make it into the famous NORMAL DISTRIBUTION [III.71 §5]. (Why should π come into it? One can give several reasons. One is that the function 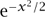 has a special role in Fourier analysis, and so does π. Another fundamental property of
has a special role in Fourier analysis, and so does π. Another fundamental property of 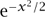 is that the function
is that the function 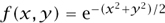 is rotationally invariant, and rotations involve circles, which involve π.)
is rotationally invariant, and rotations involve circles, which involve π.)
The last formula above is a remarkable recent discovery of David Bailey, Peter Borwein, and Simon Plouffe. The presence of the factor 1/16k leads to a way of calculating hexadecimal digits of π (that is, digits to base 16), without needing to work out all the earlier digits first. It has been used to work out digits that are astonishingly far along the hexadecimal expansion: for example, it is known that the trillionth hexadecimal digit is 8. (See MATHEMATICS: AN EXPERIMENTAL SCIENCE [VIII.5 §7] for a further discussion of this formula.)
A fact that seems paradoxical to many nonmathematicians is that a number as natural as π turns out to be IRRATIONAL, and also TRANSCENDENTAL [III.41]. However, this is not surprising at all: the defining properties of π are simple, but they do not lead to solutions of polynomial equations, so it would be extraordinary if π were not transcendental. Similarly, it would be a major surprise if one could find any pattern in the decimal digits of π. Indeed, π is conjectured to be normal to base 10, meaning that every sequence of digits occurs with about the frequency you would expect: for example, if you look at pairs of consecutive digits, then you expect 35 to occur about a hundredth of the time. However, this conjecture seems to be very hard, and it has not even been proved that the decimal expansion of π contains all the digits from 0 to 9 infinitely often.
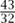 ? One possible answer is that what really matters about a number is its properties, and in particular any interesting properties it might have that distinguish it from all other numbers. Of course, we now have to decide what counts as an interesting property: for example, why do we not regard it as interesting that
? One possible answer is that what really matters about a number is its properties, and in particular any interesting properties it might have that distinguish it from all other numbers. Of course, we now have to decide what counts as an interesting property: for example, why do we not regard it as interesting that 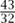 is the only number that gives you
is the only number that gives you 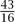 when you double it? An obvious reason is that there is an analogous property for every number x you might care to choose: x is the only number that gives you 2x when you double it. By contrast, the property “is the smallest prime number” does not mention any specific number and is easily stated in terms of a concept, that of “prime number,” whose importance is itself easy to explain. This property must apply to exactly one number, so it is likely that that number will have an important part to play in mathematics, and indeed it does. (As it happens,
when you double it? An obvious reason is that there is an analogous property for every number x you might care to choose: x is the only number that gives you 2x when you double it. By contrast, the property “is the smallest prime number” does not mention any specific number and is easily stated in terms of a concept, that of “prime number,” whose importance is itself easy to explain. This property must apply to exactly one number, so it is likely that that number will have an important part to play in mathematics, and indeed it does. (As it happens, 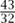 conjectured to be an important critical exponent in statistical physics, which means that it can be singled out as an interesting number, though still nothing like as fundamental as 2.)
conjectured to be an important critical exponent in statistical physics, which means that it can be singled out as an interesting number, though still nothing like as fundamental as 2.)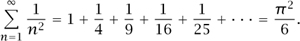
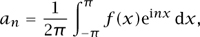
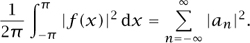
 )π and (2n +
)π and (2n + 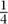 , and that |an|2 = 0 whenever n is even and nonzero. Therefore,
, and that |an|2 = 0 whenever n is even and nonzero. Therefore,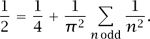
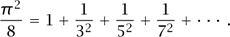
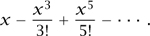
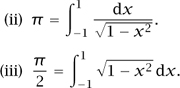
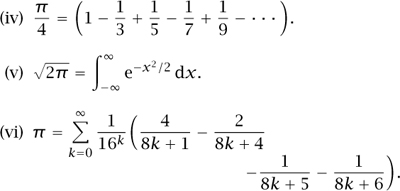
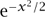 to make it into the famous NORMAL DISTRIBUTION [III.71 §5]. (Why should π come into it? One can give several reasons. One is that the function
to make it into the famous NORMAL DISTRIBUTION [III.71 §5]. (Why should π come into it? One can give several reasons. One is that the function 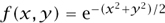 is rotationally invariant, and rotations involve circles, which involve π.)
is rotationally invariant, and rotations involve circles, which involve π.)