III.74 Quantum Computation
A quantum computer is a theoretical device that makes use of the phenomenon of “superposition” in quantum mechanics to carry out certain computations in a way that is fundamentally different from any known classical methods, and in a few important cases remarkably efficient. In classical physics, if there is some property that a particle could have, then either it has it or it does not. But according to quantum mechanics, it can exist in a sort of indeterminate state that is a linear combination of several states, in some of which it might have the property in question and in others not. The coefficients in this linear combination are called probability amplitudes: the modulus squared of the coefficient associated with a state tells you the probability of finding that the particle is in that state if you do a measurement.
Exactly what happens when you take a measurement is puzzling, and the subject of much debate among physicists and philosophers. Fortunately, however, one can understand quantum computation without solving the measurement problem, as it is called: indeed, one can get away with not understanding quantum mechanics at all. (Similarly, and for similar reasons, one could in principle do significant work in theoretical computer science without having the slightest idea what a transistor is or how it works.)
To understand quantum computation it is helpful to look at two other models of computation. The notion of a classical computation is a mathematical distillation of what actually goes on inside your computer. The “state” of a computer at any one time is modeled by an n-bit string: that is, a sequence of 0s and 1s of length n. Let us write σ for a typical string and σl, σ2, . . . , σn for the bits that make it up. A “computation” is a sequence of very simple operations performed on the initial string. For example, one operation might be to choose three numbers i, j, and k, all less than n, and change the kth bit σk of the current state σ to 1 if σi = σj = 1 and to 0 otherwise. What makes an operation such as this “simple” is that it is local in character: what it does to σ depends on, and affects, just a bounded number of bits of σ (in this case it depends on two bits and affects one). The “state space” of a classical computer, in this model, is the set {0, 1}n of all possible n-bit strings, which we shall denote by Qn.
After a certain number of stages, we declare the computation to have finished. At this point we perform a simple sequence of “measurements” on the final state, which consist in looking at the bits of the string we have ended up with. If our problem is a “decision problem,” then we will typically organize the computation so that all we need to look at is a single bit: if it is 0 then the answer is no and if it is 1 then the answer is yes.
If the ideas of the last two paragraphs are unfamiliar to you, then you are strongly advised to read the first few sections Of COMPUTATIONAL COMPLEXITY [IV.20] before continuing with this article.
The next model we shall consider is probabilistic computation. This is just like classical computation except that at each stage we are allowed to toss a (possibly biased) coin and let the simple operation we perform depend on the outcome of the toss. For instance, we might again choose three numbers i, j, and k, but this time proceed as follows: with probability 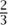 we perform the operation described earlier, and with probability
we perform the operation described earlier, and with probability 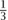 we change σk to 1 - σk. Remarkably, introducing randomness into algorithms can be extremely helpful. (Equally remarkably, there are strong theoretical reasons for believing that all algorithms that use randomness can in fact be “derandomized.” See [IV.20 §7.1] for details.)
we change σk to 1 - σk. Remarkably, introducing randomness into algorithms can be extremely helpful. (Equally remarkably, there are strong theoretical reasons for believing that all algorithms that use randomness can in fact be “derandomized.” See [IV.20 §7.1] for details.)
Suppose that we allow our randomized probabilistic computation to run for k steps and that we do not examine the result. How should we model the current state of the computer? We could use exactly the same definition as in the classical case—a state is an n-bit string—and simply say that the computation is in a state that we cannot know until we do a measurement. But the state of the computer is not a complete mystery: for each n-bit string σ there will be some probability pσ that the state is σ. In other words, it is better to think of the state of the computer as a PROBABILITY DISTRIBUTION [III.71] on Qn. This probability distribution will depend on the initial string, and therefore it can in principle give us useful information about that string.
Here is how to use a randomized computation to solve a decision problem. Let us write P(σ) for the probability that a certain bit (without loss of generality the first) is 1 at the end of the computation, when the initial string is σ. Suppose we can arrange for P(σ) to be at least a for all strings σ for which the answer is yes, and at most some smaller number b for all strings σ for which the answer is no. Let c be the average of a and b. Now run the computation m times for some large m. With very high probability, if the answer is yes then when we have finished the first bit will have been 1 more than cm times, and if the answer is no then it will have been 1 fewer than cm times. So we can solve the decision problem, not with certainty, but at least with a negligibly small chance of error.
The “state space” of a probabilistic computer consists of all possible probability distributions on Qn, or equivalently all possible functions p : Qn → [0, 1] such that Σσ∈Qn = 1. The state space of a quantum computer also consists of functions defined on Qn, but there are two differences. First, they can take complex as well as real values. Second, if 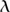 : Qn → ℂ is a state, then the requirement on the size of
: Qn → ℂ is a state, then the requirement on the size of 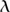 is that Σσ∈Qn |
is that Σσ∈Qn |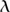 |2 = 1. In other words,
|2 = 1. In other words, 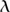 is a unit vector in the HILBERT SPACE [III.37]
is a unit vector in the HILBERT SPACE [III.37] 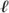 2(Qn, ℂ) rather than a nonnegative unit vector in the SANACB SPACE [III.62]
2(Qn, ℂ) rather than a nonnegative unit vector in the SANACB SPACE [III.62] 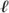 1 (Qn, ℝ). The scalars
1 (Qn, ℝ). The scalars 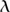 σ are the probability amplitudes mentioned earlier. We shall explain what this means later.
σ are the probability amplitudes mentioned earlier. We shall explain what this means later.
Among the possible states of a quantum computer are the “basis states,” which are the functions that take the value 1 at one string and 0 everywhere else. It is customary to use Dirac’s “bra” and “ket” notation for these, writing |σ〉 if the string in question is σ. Other “pure states” are then linear combinations of these, and Dirac’s notation is again used. For instance, if n = 5, then one fairly simple state that the computer could be in is |ψ〉 = (1/ )|01101〉 + (i/
)|01101〉 + (i/ )|11001〉.
)|11001〉.
To get from one state to another, we again apply “local” operations, but adapted to the new, Hilbert space context. Suppose first that we have a basis state |σ〉. Again we look at a very small number of bits. If, for instance, we look at three bits, at i, j, and k, then there are eight possibilities for the triple τ = (σ1, σ2, σ3), which we could think of as the basis states in a much smaller state space: the space of all functions μ : Q3 → ℂ such that Στ∈Q3 |μτ2 = 1. The obvious operations that take unit vectors to unit vectors in a complex Hilbert space are the UNITARY MAPS [III.50 §3.1], and these are indeed what are used.
Let us illustrate this with an example. Suppose that n = 5, and that i, j, and k are 1, 2, and 4. One possible operation on these three bits would send |000〉 to (|000〉 + i|111〉)/ and |111〉 to (i|000〉 + |111〉)/
and |111〉 to (i|000〉 + |111〉)/ , leaving all other three-bit sequences as they are. If our initial basis state is |01000〉, then the first, second, and fourth bits are in the state |000〉, so the resulting state at the end of the operation would be (|01000〉 + i|11110〉)/
, leaving all other three-bit sequences as they are. If our initial basis state is |01000〉, then the first, second, and fourth bits are in the state |000〉, so the resulting state at the end of the operation would be (|01000〉 + i|11110〉)/ .
.
Now that we have explained what a basic operation does to a basis state, we have in fact explained what it does in general, since the basis states form a basis of the state space. In other words, if you start with a linear combination (or superposition) of basis states, you apply the operation described above to each basis state and take the corresponding linear combination of the results.
Thus, an elementary operation of quantum computation consists in acting on the state space by means of a very special sort of unitary map. If the operation is on k bits (where k is typically very small indeed), then the matrix of this map will be a diagonal sum of 2n-k copies of the 2k × 2k unitary matrix used to manipulate those k bits (if the basis elements are appropriately ordered). A quantum computation is a sequence of these elementary operations.
Measuring the result of a quantum computation is more mysterious. The basic idea is simple: we do a certain number of elementary operations and then look at one of the bits of the resulting state. But what does this mean, when the state is not a basis state but rather a superposition of such states? The answer is that when we “measure” the rth bit of the output, we are doing a probabilistic process that is somewhat different from the measurement of a probabilistic computation: if the output state is Σσ∈Qn 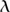 σ |σ〉, then the probability that we observe 1 is the sum of all |
σ |σ〉, then the probability that we observe 1 is the sum of all |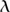 σ|2 such that the kth bit of σ is 1, and the probability that we observe 0 is the same sum but over those σ for which the kth bit is 0. This is why the numbers
σ|2 such that the kth bit of σ is 1, and the probability that we observe 0 is the same sum but over those σ for which the kth bit is 0. This is why the numbers 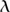 σ are called probability amplitudes. In order to get a useful answer from a quantum computation, one runs it several times, just as with a probabilistic computation.
σ are called probability amplitudes. In order to get a useful answer from a quantum computation, one runs it several times, just as with a probabilistic computation.
Note the following two important differences between a quantum computation and a probabilistic computation. We described the state of a probabilistic computation as a probability distribution on Qn, which one could also call a convex combination of basis states. But this probability distribution is not telling us what is in the computer: that is a basis state. Rather, it is describing our knowledge about what is in the computer. By contrast, the state of a quantum computer really is a unit vector in a 2n-dimensional Hilbert space. So in a certain sense a huge amount of computation can go on in parallel: this is what gives quantum computation its power. Although we cannot know much about the computation, since a single measurement causes it to “collapse,” we can hope to organize it so that different parts of it “interfere” with each other. This “interference” is related to the second main difference, which is the fact that we deal with probability amplitudes rather than probabilities. Roughly speaking, a quantum computation can “split up” and “reassemble itself,” whereas once a probabilistic computation splits up it stays split up. Crucial to the reassembly process in a quantum computation is cancelation of probability amplitudes: to give an extreme example, if you multiply a typical unitary matrix by its inverse, then there is a huge amount of cancelation to get all the off-diagonal entries of the resulting matrix to be zero.
All this raises two obvious questions: what are quantum computers good for, and can they actually be built? It turns out that a quantum computer can carry out classical and probabilistic computations, so the first question is asking whether they can do anything further.1 One might think so, since the state space is so much bigger than it is for a classical computation (it is 2n dimensional rather than merely n dimensional), and the reassembly process means that we can potentially afford to visit remote parts of the state space, where all coefficients might be of very similar (and small) magnitudes, and come back again to a state where a useful measurement can be made. However, the very vastness of this space means that most states are completely inaccessible unless one is prepared to use a vast number of basic operations. Additionally, it is important that at the end of the computation the output should not be a “typical” state, since only very special states give rise to useful measurements.
These arguments show that if a quantum computation is to be useful, then it will have to be very carefully (and cleverly) organized. However, there is a spectacular example of just such a computation: Peter Shor’s use of a quantum computer to calculate FAST FOURIER TRANSFORMS [III.26] extremely rapidly. The fast Fourier transform has a symmetry that allows the calculation to be split up and carried out “in parallel” (it might be better to say “in superposition”) in a way that is ideally suited to a quantum computer. A super-fast Fourier transform can then be used to solve (by classical methods) some famous computational problems, such as the discrete logarithm problem and the factorization of large integers. The latter can then be used to break a public-key cryptosystem, the encryption method that lies at the heart of modern computer security. (See MATHEMATICS AND CRYPTOGRAPHY [VII. 7 §5] and COMPUTATIONAL NUMBER THEORY [IV.3 §3] for further discussion of these problems.)
Can a machine be built that would actually be able to do this? There are formidable problems to overcome, arising from a phenomenon in quantum mechanics known as “decoherence,” which makes it very hard to stop a complicated state from “collapsing” to a simpler one that is no longer of use. Some progress has been made, but it is too early to say whether, or when, a quantum computer will be built that can factorize large numbers quickly.
Nevertheless, the theoretical challenges raised by the notion of a quantum computer are fascinating. Perhaps the most interesting one is very simple: find an application of quantum computers that is significantly different from the few that have already been found. The fact that quantum computers can factorize large numbers is strong evidence that they are more powerful, but it would be good to have a better understanding of why. (It is known that quantum computers are better for some other uses, such as COMMUNICATION COMPLEXITY [IV.20§5.1.4].) Is there a much simpler task that is easy for quantum computers and difficult for classical computers, at least if some well-known plausible hypothesis is true about what classical computers cannot do? Can quantum computers solve NP-COMPLETE [IV.20 §4] problems? The majority opinion is that they cannot, and indeed the statement that they cannot is becoming another of the many “plausible hypotheses” of complexity theory, but it would be good to have stronger reasons for believing in this statement, such as a proof subject to already-known plausible hypotheses in classical computation.
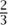 we perform the operation described earlier, and with probability
we perform the operation described earlier, and with probability 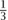 we change σk to 1 - σk. Remarkably, introducing randomness into algorithms can be extremely helpful. (Equally remarkably, there are strong theoretical reasons for believing that all algorithms that use randomness can in fact be “derandomized.” See [IV.20 §7.1] for details.)
we change σk to 1 - σk. Remarkably, introducing randomness into algorithms can be extremely helpful. (Equally remarkably, there are strong theoretical reasons for believing that all algorithms that use randomness can in fact be “derandomized.” See [IV.20 §7.1] for details.)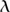 : Qn → ℂ is a state, then the requirement on the size of
: Qn → ℂ is a state, then the requirement on the size of 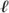 2(Qn, ℂ) rather than a nonnegative unit vector in the SANACB SPACE [III.62]
2(Qn, ℂ) rather than a nonnegative unit vector in the SANACB SPACE [III.62]  )|01101〉 + (i/
)|01101〉 + (i/