III.76 Quaternions, Octonions, and Normed Division Algebras
Mathematics took a leap forward in sophistication with the introduction of the COMPLEX NUMBERS [I.3 §1.5]. To define these, one suspends one’s disbelief, introduces a new number i, and declares that i2 = -1. A typical complex number is of the form a + ib, and the arithmetic of complex numbers is easy to deduce from the normal rules of arithmetic for real numbers. For example, to calculate the product of 1 + 2i and 2 + i one simply expands some brackets:
(1 + 2i)(2 + i) 2 + 5i + 2i2 = 5i,
the last equality following from the fact that i2 = -1. One of the great advantages of the complex numbers is that, if complex roots are allowed, every polynomial can be factorized into linear factors: this is the famous FUNDAMENTAL THEOREM OF ALGEBRA [V.13].
Another way to define a complex number is to say that it is a pair of real numbers. That is, instead of writing a + ib one writes simply (a, b). To add two complex numbers is simple, and exactly what one does when adding two vectors: (a, b) + (c, d) = (a + c, b + d). However, it is less obvious how to multiply: the product of (a, b) and (c, d) is (ac - bd, ad + bc), which seems an odd definition unless one goes back to thinking of (a, b) and (c, d) as a + ib and c + id.
Nevertheless, the second definition draws our attention to the fact that the complex numbers are formed out of the two-dimensional VECTOR SPACE [I.3 §2.3] ℝ2 with a carefully chosen definition of multiplication. This immediately raises a question: could we do the same for higher-dimensional spaces?
As it stands, this question is not wholly precise, since we have not been clear about what “the same” means. To make it precise, we must ask what properties this multiplication should have. So let us return to ℝ2 and think about why it would be a bad idea to define the product of (a, b) and (c, d) in a simple-minded way as (ac, bd). Of course, part of the reason is that the product of a + ib and c + id is not ac + ibd, but why should we not also be interested in other ways of multiplying vectors in ℝ2?
The trouble with this alternative definition is that it allows zero divisors, that is, pairs of nonzero numbers that multiply together to give zero. For example, it gives us (1, 0)(0, 1) = (0, 0). If we have zero divisors, then we cannot have multiplicative inverses, since if every nonzero number in a number system has a multiplicative inverse, and if xy = 0, then either x = 0 or y = x-1 xy = x-1 0 = 0. And if we do not have multiplicative inverses, then we cannot define a useful notion of division.
Let us return then to the usual definition of the complex numbers and try to think how we can go beyond it. One way we might try to “do the same” as we did before is to do to the complex numbers what we did to the real numbers. That is, why not define a “super-complex” number to be an ordered pair (z, w) of complex numbers? Since we still want to have a vector space, we will continue to define the sum of (z, w) and (u, v) to be (z + u, w + v), but we need to think about the best way of defining their product. An obvious guess is to use precisely the expression that worked before, namely (zu - wv, zv + wu). But if we do that, then the product of (l, i) and (1, -i) works out to be (1 + i2, i - i) = (0, 0), so we have zero divisors.
This example came from the following thought. The modulus of a complex number z = a + ib, which measures the length of the vector (a, b), is the real number |z| = 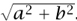 . This can also be written as
. This can also be written as 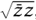 , where
, where 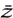 is the complex conjugate a - ib of z. Now if a and b are allowed to take complex values, then there is no reason for a2 + b2 to be nonnegative, so we may not be able to take its square root. Moreover, if a2 + b2 = 0 it does not follow that a = b = 0. The example above came from taking a = 1 and b = i and multiplying the number (1, i) by its “conjugate” (1, -i).
is the complex conjugate a - ib of z. Now if a and b are allowed to take complex values, then there is no reason for a2 + b2 to be nonnegative, so we may not be able to take its square root. Moreover, if a2 + b2 = 0 it does not follow that a = b = 0. The example above came from taking a = 1 and b = i and multiplying the number (1, i) by its “conjugate” (1, -i).
There is, nevertheless, a natural way to define the modulus of a pair (z, w) that works even when z and w are complex numbers. The number |z|2 + |w|2 is guaranteed to be nonnegative, so we can take its square root. Moreover, if z = a + ib and w = c + id, then we will obtain the number (a2 + b2 + c2 + d2)1/2, which is the length of the vector (a, b, c, d).
This observation leads to another: the complex conjugate of a real number is the number itself, so, if we want to “use the same formula” for the complex numbers as we used for the reals, we are free to introduce complex conjugates into that formula. Before we try to do that, let us think about what we might mean by the “conjugate” of a pair (z, w). We expect (z, 0) to behave like the complex number z, so its conjugate should be (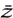 , 0). Similarly, if z and w are real, then the conjugate of (z, w) should be (z, -w). This leaves us with two reasonable possibilities for a general pair (z, w): either (
, 0). Similarly, if z and w are real, then the conjugate of (z, w) should be (z, -w). This leaves us with two reasonable possibilities for a general pair (z, w): either (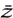 , -
, -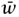 ) or (
) or (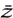 , -w). Let us consider the second of these.
, -w). Let us consider the second of these.
We would like the product of (z,w) and its conjugate, which we are defining as (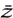 , -w), to be (|z|2 + |w|2, 0). We want to achieve this by introducing complex conjugates into the formula
, -w), to be (|z|2 + |w|2, 0). We want to achieve this by introducing complex conjugates into the formula
(z, w) (u, v) = (zu - wv, zv + wu).
An obvious way of getting the result we want is to take
(z, w)(u, v) = (zu - 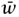 v,
v, 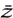 v + wu),
v + wu),
and this modified formula, it turns out, defines an ASSOCIATIVE BINARY OPERATION [I.2 §2.4] On the set Of pairs (z, w). If you try the other definition of conjugate, you will find that you end up with zero divisors. (A first indication of trouble is that, under the other definition, the pair (0, i) is its own conjugate.)
We have just defined the quaternions, a set  of “numbers” that form a four-dimensional real vector space, or alternatively a two-dimensional complex vector space. (The letter “H” is in honor of William Rowan Hamilton, their discoverer. See HAMILTON [VI.37] for the story of how the discovery was made.) But why should we have wished to do that? This question becomes particularly pressing when we notice that the notion of multiplication that we have defined is not commutative. For example, (0, 1)(i, 0) = (0, i), while (i, 0)(0, 1) = (0, -i).
of “numbers” that form a four-dimensional real vector space, or alternatively a two-dimensional complex vector space. (The letter “H” is in honor of William Rowan Hamilton, their discoverer. See HAMILTON [VI.37] for the story of how the discovery was made.) But why should we have wished to do that? This question becomes particularly pressing when we notice that the notion of multiplication that we have defined is not commutative. For example, (0, 1)(i, 0) = (0, i), while (i, 0)(0, 1) = (0, -i).
To answer it, let us take a step back and think about the complex numbers again. The most obvious justification for introducing those is that one can use them to solve all polynomial equations, but that is by no means the only justification. In particular, complex numbers have an important geometrical interpretation, as rotations and enlargements. This connection becomes particularly clear if we choose yet another way of writing the complex number a + ib, as the matrix 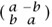 . Multiplication by the complex number a + ib can be thought of as a LINEAR MAP [I.3 §4.2] on the plane ℝ2, and this is the matrix of that linear map. For example, the complex number i corresponds to the matrix
. Multiplication by the complex number a + ib can be thought of as a LINEAR MAP [I.3 §4.2] on the plane ℝ2, and this is the matrix of that linear map. For example, the complex number i corresponds to the matrix 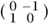 , which is the matrix of a counterclockwise rotation through
, which is the matrix of a counterclockwise rotation through  π about the origin, and this rotation is exactly what multiplying by i does to the complex plane.
π about the origin, and this rotation is exactly what multiplying by i does to the complex plane.
If complex numbers can be thought of as linear maps from ℝ2 to ℝ2, then quaternions should have an interpretation as linear maps from ℂ2 to ℂ2. And indeed they do. Let us associate with the pair (z, w) the matrix 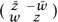 . Now let us consider the product of two such matrices:
. Now let us consider the product of two such matrices:
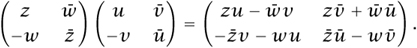
This product is precisely the matrix associated with the pair (zu - w , zv + w
, zv + w ), which is the quaternionic product of (z, w) and (u, v)! As an immediate corollary, we have a proof of a fact mentioned earlier: that quaternionic multiplication is associative. Why? Because matrix multiplication is associative. (And that is true because the composition of functions is associative: see [I.3 §3.2].)
), which is the quaternionic product of (z, w) and (u, v)! As an immediate corollary, we have a proof of a fact mentioned earlier: that quaternionic multiplication is associative. Why? Because matrix multiplication is associative. (And that is true because the composition of functions is associative: see [I.3 §3.2].)
Notice that the DETERMINANT [III.15] of the matrix 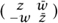 |z|2 + |w|2, so the modulus of the pair (z, w) (which is defined to be
|z|2 + |w|2, so the modulus of the pair (z, w) (which is defined to be 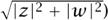 is just the determinant of the associated matrix. This proves that the modulus of the product of two quaternions is the product of their moduli (since the determinant of a product is the product of determinants). Notice also that the adjoint of the matrix (that is, the complex conjugate of the transpose matrix) is
is just the determinant of the associated matrix. This proves that the modulus of the product of two quaternions is the product of their moduli (since the determinant of a product is the product of determinants). Notice also that the adjoint of the matrix (that is, the complex conjugate of the transpose matrix) is 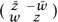 , which is the matrix associated with the conjugate pair (
, which is the matrix associated with the conjugate pair (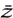 , - w). Finally, notice that if |z|2 + |w|2 = 1, then
, - w). Finally, notice that if |z|2 + |w|2 = 1, then
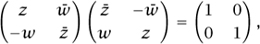
which tells us that the matrix is UNITARY [III.50 §3.1]. Conversely, any unitary 2 × 2 matrix with determinant 1 can easily be shown to have the form 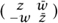 . Therefore, the unit quaternions (that is, the quaternions of modulus 1) have a geometrical interpretation: they correspond to the “rotations” of ℂ2 (that is, the unitary maps of determinant 1), just as the unit complex numbers correspond to the rotations of ℝ2.
. Therefore, the unit quaternions (that is, the quaternions of modulus 1) have a geometrical interpretation: they correspond to the “rotations” of ℂ2 (that is, the unitary maps of determinant 1), just as the unit complex numbers correspond to the rotations of ℝ2.
The group of unitary transformations of ℂ2 of determinant 1 is an important LIE GROUP [III.48 §1] called the special unitary group SU(2). Another important Lie group is the group SO(3), of rotations of ℝ3. Surprisingly, the unit quaternions can be used to describe this group as well. To see this, it is convenient to present the quaternions in another, more conventional, way.
Quaternions, as they are usually introduced, are a system of numbers where we introduce not just one square root of -1 but three, called i, j, and k (together with their negatives). Once one knows that i2 = j2 = k2 = -1, and also that ij = k, jk = i, and ki = j, one has all the information one needs to multiply two quaternions. For example, ji = jjk = -k. A typical quaternion takes the form a+ib+jc+kd, which corresponds to the pair of complex numbers (a + ic, b + id) in our previous way of thinking about quaternions. Now if we want, we can think of this quaternion as a pair (a, v), where a is a real number and v is the vector (b, c, d) in ℝ3. The product of (a, v) and (b, w) then works out to be (ab - v ·w, aw + bv + v ∧ w), where v · w and v ∧ w are the scalar and vector products of v and w.
If q = (a, u) is a quaternion of modulus 1, then a2 + ||u||2 = 1, so we can write q in the form (cos θ, v sin θ) with v a unit vector. This quaternion corresponds to a counterclockwise rotation R about an axis in direction v through an angle of 2θ. This angle is not what one might at first expect, and neither is the way the correspondence works. If w is another vector, we can represent it as the quaternion (0, w). We would now like a neat expression for the quaternion (0, Rw); it turns out that (0, Rw) = q(0, w)q*, where q* is the conjugate (cos θ, -v sin θ) of q, which is also its multiplicative inverse, as q has modulus 1. So to do the rotation R, you do not multiply by q but rather you conjugate by q. (This is a different meaning of the word “conjugate,” referring to multiplying on one side by q and on the other side by q-1.) Now if q1 and q2 are quaternions corresponding to rotations R1 and R2, respectively, then
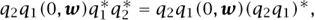
from which it follows that q2q1 corresponds to the rotation R2R1. This tells us that quaternionic multiplication corresponds to composition of rotations.
The unit quaternions form a group, as we have already seen—it is SU(2). It might appear that we have shown that SU(2) is the same as the group SO(3) of rotations of ℝ3. However, we have not quite done this, because for each rotation of ℝ3 there are two unit quaternions that give rise to it. The reason is simple: a counterclockwise rotation through θ about a vector v is the same as a counterclockwise rotation through -θ about -v. In other words, if q is a unit quaternion, then q and -q give rise to the same rotation of ℝ3. So SU(2) is not isomorphic to SO(3); rather, it is a double cover of SO(3). This fact has important ramifications in mathematics and physics. In particular, it lies behind the notion of the “spin” of an elementary particle.
Let us return to the question we were considering earlier: for which n is there a good way of multiplying vectors in ℝn? We now know that we can do it for n = 1, 2, or 4. When n = 4 we had to sacrifice commutativity, but we were amply rewarded for this, since quaternion multiplication gives a very concise way of representing the important groups SU(2) and SO(3). These groups are not commutative, so it was essential to our success that quaternion multiplication should also not be commutative.
One obvious thing we can do is continue the process that led to the quaternions. That is, we can consider pairs (q, r) of quaternions, and multiply these pairs together using the formula
(q, r)(s, t) = (qs - r* t, q* t + rs).
Since the conjugate q* of a quaternion q is the analogue of the complex conjugate 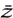 of a complex number z, this is basically the same formula that we used for multiplication of pairs of complex numbers—that is, for quaternions.
of a complex number z, this is basically the same formula that we used for multiplication of pairs of complex numbers—that is, for quaternions.
However, we need to be careful: multiplication of quaternions is not commutative, so there are in fact many formulas we could write down that would be “basically the same” as the earlier one. Why choose the above one, rather than, say, replacing q* t by tq*?
It turns out that the formula suggested above leads to zero divisors. For example, (j, i)(l, k) works out to be (0, 0). However, the modified formula
(q, r)(s, t) = (qs - tr*, q* t + sr),
which one can discover fairly quickly if one bears in mind that one would like (q, r)(q*, - r) to work out as (|q|2 + |r|2, 0), does produce a useful number system. It is denoted 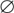 and its elements are called the octonions (or sometimes the Cayley numbers). Unfortunately, multiplication of octonions is not even associative, but it does have two very good properties: every nonzero octonion has a multiplicative inverse, and two nonzero octonions never multiply together to give zero. (Because octonion multiplication is not associative, these two properties are no longer obviously equivalent. However, any subalgebra of the octonions generated by two elements is associative, and this is enough to prove the equivalence.)
and its elements are called the octonions (or sometimes the Cayley numbers). Unfortunately, multiplication of octonions is not even associative, but it does have two very good properties: every nonzero octonion has a multiplicative inverse, and two nonzero octonions never multiply together to give zero. (Because octonion multiplication is not associative, these two properties are no longer obviously equivalent. However, any subalgebra of the octonions generated by two elements is associative, and this is enough to prove the equivalence.)
So now we have number systems when n = 1, 2, 4, or 8. It turns out that these are the only dimensions with good notions of multiplication. Of course, “good” has a technical meaning here: matrix multiplication, which is associative but gives zero divisors, is for many purposes “better” than octonion multiplication, which has no zero divisors but is not associative. So let us finish by seeing more precisely what it is that is special about dimensions 1, 2, 4, and 8.
All the number systems constructed above have a notion of size given by a NORM [III.62]. For real and complex numbers z, the norm of z is just its modulus. For a quaternion or octonion x, it is defined to be 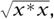 where x* is the conjugate of x (a definition that works for real and complex numbers as well). If we write ||x|| for the norm of x, then the norms constructed have the property that ||xy|| = ||x|| ||y|| for every x and y. This property is extremely useful: for example, it tells us that the elements of norm 1 are closed under multiplication, a fact that we used many times when discussing the geometric importance of complex numbers and quaternions.
where x* is the conjugate of x (a definition that works for real and complex numbers as well). If we write ||x|| for the norm of x, then the norms constructed have the property that ||xy|| = ||x|| ||y|| for every x and y. This property is extremely useful: for example, it tells us that the elements of norm 1 are closed under multiplication, a fact that we used many times when discussing the geometric importance of complex numbers and quaternions.
The feature that distinguishes dimensions 1, 2, 4, and 8 from all other dimensions is that these are the only dimensions for which one can define a norm ||·|| and a notion of multiplication with the following properties.
(i) There is a multiplicative identity: that is, a number 1 such that 1x = x1 = x for every x.
(ii) Multiplication is bilinear, meaning that x(y + z) = xy + xz for every x, y, and z, and x(ay) = a(xy) whenever a is a real number, and similarly for multiplication on the right.
(iii) For any x and y, ||xy|| = ||x|| ||y|| (and therefore there are no zero divisors).
A formed division algebra is a vector space ℝn together with a norm and a method of multiplying vectors that satisfy the above properties. So normed division algebras exist only in dimensions 1, 2, 4, and 8. Furthermore, even in these dimensions, ℝ, ℂ,  , and
, and 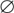 are the only examples.
are the only examples.
There are various ways to prove this fact, which is known as Hurwitz’s theorem. Here is a very brief sketch of one of them. The idea is to prove that if a normed division algebra A contains one of the above examples, then either it is that example, or it contains the next one in the sequence. So either A is one of ℝ, ℂ,  , and
, and 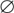 or A contains the algebra produced by doing to
or A contains the algebra produced by doing to 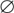 the process we used to construct
the process we used to construct  from ℂ and
from ℂ and 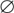 from
from  , a process known as the Cayley–Dickson construction. However, if one applies the Cayley–Dickson construction to
, a process known as the Cayley–Dickson construction. However, if one applies the Cayley–Dickson construction to 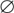 , one obtains an algebra with zero divisors.
, one obtains an algebra with zero divisors.
To see how such an argument might work, let us imagine, for the sake of example, that A contains 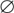 as a proper subalgebra. It turns out that the norm on A must be a EUCLIDEAN NORM [III.37]—that is, a norm derived from an inner product. (Roughly speaking, this is because multiplication by an element of norm 1 does not change the norm, which gives A so many symmetries that the norm on A has to be the most symmetric of all, namely Euclidean.) Let us call an element of A imaginary if it is orthogonal to the element 1. Then we can define a conjugation operation on A by taking 1* to be 1 and x* to be -x when x is imaginary, and extending linearly. This operation can be shown to have all the properties one would like. In particular, aa* = a*a = ||a||2 for every element a of A. Let us choose a norm-1 element of A that is orthogonal to all of
as a proper subalgebra. It turns out that the norm on A must be a EUCLIDEAN NORM [III.37]—that is, a norm derived from an inner product. (Roughly speaking, this is because multiplication by an element of norm 1 does not change the norm, which gives A so many symmetries that the norm on A has to be the most symmetric of all, namely Euclidean.) Let us call an element of A imaginary if it is orthogonal to the element 1. Then we can define a conjugation operation on A by taking 1* to be 1 and x* to be -x when x is imaginary, and extending linearly. This operation can be shown to have all the properties one would like. In particular, aa* = a*a = ||a||2 for every element a of A. Let us choose a norm-1 element of A that is orthogonal to all of 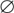 and call it i. Then i* = -i, so 1 = i*i = -i2, so i2 = -1. Now take the algebra generated by i and the copy of
and call it i. Then i* = -i, so 1 = i*i = -i2, so i2 = -1. Now take the algebra generated by i and the copy of 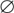 that lies in A. With some algebraic manipulation, one can demonstrate that this consists of elements of the form x + iy, with x and y belonging to
that lies in A. With some algebraic manipulation, one can demonstrate that this consists of elements of the form x + iy, with x and y belonging to 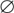 . Moreover, the product of x + iy and z + iw turns out to be xz - wy* + i(x*w + zy), which is exactly what the Cayley–Dickson construction gives.
. Moreover, the product of x + iy and z + iw turns out to be xz - wy* + i(x*w + zy), which is exactly what the Cayley–Dickson construction gives.
For further details about quaternions and octonions, two excellent sources are a discussion by John Baez at http://math.ucr.edu/home/baez/octonions and a book, On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, by J. H. Conway and D. A. Smith (2003; Wellesley, MA: AK Peters).
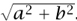 . This can also be written as
. This can also be written as 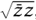 , where
, where 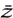 is the complex conjugate a - ib of z. Now if a and b are allowed to take complex values, then there is no reason for a2 + b2 to be nonnegative, so we may not be able to take its square root. Moreover, if a2 + b2 = 0 it does not follow that a = b = 0. The example above came from taking a = 1 and b = i and multiplying the number (1, i) by its “conjugate” (1, -i).
is the complex conjugate a - ib of z. Now if a and b are allowed to take complex values, then there is no reason for a2 + b2 to be nonnegative, so we may not be able to take its square root. Moreover, if a2 + b2 = 0 it does not follow that a = b = 0. The example above came from taking a = 1 and b = i and multiplying the number (1, i) by its “conjugate” (1, -i).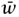 ) or (
) or ( of “numbers” that form a four-dimensional real vector space, or alternatively a two-dimensional complex vector space. (The letter “H” is in honor of William Rowan Hamilton, their discoverer. See HAMILTON [VI.37] for the story of how the discovery was made.) But why should we have wished to do that? This question becomes particularly pressing when we notice that the notion of multiplication that we have defined is not commutative. For example, (0, 1)(i, 0) = (0, i), while (i, 0)(0, 1) = (0, -i).
of “numbers” that form a four-dimensional real vector space, or alternatively a two-dimensional complex vector space. (The letter “H” is in honor of William Rowan Hamilton, their discoverer. See HAMILTON [VI.37] for the story of how the discovery was made.) But why should we have wished to do that? This question becomes particularly pressing when we notice that the notion of multiplication that we have defined is not commutative. For example, (0, 1)(i, 0) = (0, i), while (i, 0)(0, 1) = (0, -i).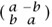 . Multiplication by the complex number a + ib can be thought of as a LINEAR MAP [I.3 §4.2] on the plane ℝ2, and this is the matrix of that linear map. For example, the complex number i corresponds to the matrix
. Multiplication by the complex number a + ib can be thought of as a LINEAR MAP [I.3 §4.2] on the plane ℝ2, and this is the matrix of that linear map. For example, the complex number i corresponds to the matrix 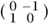 , which is the matrix of a counterclockwise rotation through
, which is the matrix of a counterclockwise rotation through  π about the origin, and this rotation is exactly what multiplying by i does to the complex plane.
π about the origin, and this rotation is exactly what multiplying by i does to the complex plane.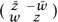 . Now let us consider the product of two such matrices:
. Now let us consider the product of two such matrices: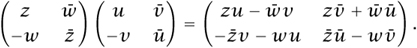
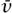 , zv + w
, zv + w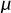 ), which is the quaternionic product of (z, w) and (u, v)! As an immediate corollary, we have a proof of a fact mentioned earlier: that quaternionic multiplication is associative. Why? Because matrix multiplication is associative. (And that is true because the composition of functions is associative: see [I.3 §3.2].)
), which is the quaternionic product of (z, w) and (u, v)! As an immediate corollary, we have a proof of a fact mentioned earlier: that quaternionic multiplication is associative. Why? Because matrix multiplication is associative. (And that is true because the composition of functions is associative: see [I.3 §3.2].)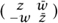 |z|2 + |w|2, so the modulus of the pair (z, w) (which is defined to be
|z|2 + |w|2, so the modulus of the pair (z, w) (which is defined to be 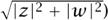 is just the determinant of the associated matrix. This proves that the modulus of the product of two quaternions is the product of their moduli (since the determinant of a product is the product of determinants). Notice also that the adjoint of the matrix (that is, the complex conjugate of the transpose matrix) is
is just the determinant of the associated matrix. This proves that the modulus of the product of two quaternions is the product of their moduli (since the determinant of a product is the product of determinants). Notice also that the adjoint of the matrix (that is, the complex conjugate of the transpose matrix) is 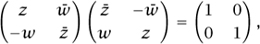
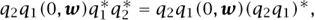
 and its elements are called the octonions (or sometimes the Cayley numbers). Unfortunately, multiplication of octonions is not even associative, but it does have two very good properties: every nonzero octonion has a multiplicative inverse, and two nonzero octonions never multiply together to give zero. (Because octonion multiplication is not associative, these two properties are no longer obviously equivalent. However, any subalgebra of the octonions generated by two elements is associative, and this is enough to prove the equivalence.)
and its elements are called the octonions (or sometimes the Cayley numbers). Unfortunately, multiplication of octonions is not even associative, but it does have two very good properties: every nonzero octonion has a multiplicative inverse, and two nonzero octonions never multiply together to give zero. (Because octonion multiplication is not associative, these two properties are no longer obviously equivalent. However, any subalgebra of the octonions generated by two elements is associative, and this is enough to prove the equivalence.)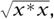 where x* is the conjugate of x (a definition that works for real and complex numbers as well). If we write ||x|| for the norm of x, then the norms constructed have the property that ||xy|| = ||x|| ||y|| for every x and y. This property is extremely useful: for example, it tells us that the elements of norm 1 are closed under multiplication, a fact that we used many times when discussing the geometric importance of complex numbers and quaternions.
where x* is the conjugate of x (a definition that works for real and complex numbers as well). If we write ||x|| for the norm of x, then the norms constructed have the property that ||xy|| = ||x|| ||y|| for every x and y. This property is extremely useful: for example, it tells us that the elements of norm 1 are closed under multiplication, a fact that we used many times when discussing the geometric importance of complex numbers and quaternions.