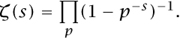III.80 The Riemann Zeta Function
The Riemann zeta function ζ is a function defined on the complex numbers that encapsulates in a remarkable way many of the most important properties about the distribution of prime numbers. If s is a complex number with real part greater than 1, then ζ(s) is defined to be 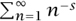 . The condition that Re(s) > 1 is needed to ensure that this series converges. However, because the resulting function is HOLOMORPHIC [I.3 §5.6], it is possible to extend the definition by means of analytic continuation. The result is a function that is defined everywhere on the complex plane (though it takes the value ∞ at 1).
. The condition that Re(s) > 1 is needed to ensure that this series converges. However, because the resulting function is HOLOMORPHIC [I.3 §5.6], it is possible to extend the definition by means of analytic continuation. The result is a function that is defined everywhere on the complex plane (though it takes the value ∞ at 1).
A first clue to why this function is related to the distribution of primes is Euler’s product formula:
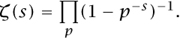
Here, the product on the right-hand side is over all primes. The formula can be proved by writing (1 - p-s)-1 as 1 + p-s + p-2s + · · · , expanding out the product, and using THE FUNDAMENTAL THEOREM OF ARITHMETIC [V.14]. Deeper connections were discovered by RIEMANN [VI.49], who formulated the famous RIEMANN HYPOTHESIS [IV.2 §3].
The Riemann zeta function is just one of a family of functions that encode important number-theoretic information. For example, the Dirichlet L-functions are closely related to the distribution of primes in arithmetic progressions. For more details about these and about the Riemann zeta function itself, see ANALYTIC NUMBER THEORY [IV.2]. Some more sophisticated zeta functions are described in THE WEIL CONJECTURES [V.35]. See also L-FUNCTIONS [III.47].
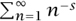 . The condition that Re(s) > 1 is needed to ensure that this series converges. However, because the resulting function is HOLOMORPHIC [I.3 §5.6], it is possible to extend the definition by means of analytic continuation. The result is a function that is defined everywhere on the complex plane (though it takes the value ∞ at 1).
. The condition that Re(s) > 1 is needed to ensure that this series converges. However, because the resulting function is HOLOMORPHIC [I.3 §5.6], it is possible to extend the definition by means of analytic continuation. The result is a function that is defined everywhere on the complex plane (though it takes the value ∞ at 1).