III.81 Rings, Ideals, and Modules
1 Rings
A ring, like a GROUP [I.3 §2.1] or a FIELD [I.3 §2.2], is an algebraic structure that satisfies certain axioms. To remember the axioms for both rings and fields at the same time, it is helpful to think of two simple examples: with the two operations of addition and multiplication, the set 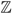 of all integers forms a ring and the set ℚ of all rational numbers forms a field. In general, a ring is a set R with two BINARY OPERATIONS [I.2 §2.4], denoted by “+” and “×”, which satisfies all the field axioms apart from the one that says that nonzero elements have multiplicative inverses.
of all integers forms a ring and the set ℚ of all rational numbers forms a field. In general, a ring is a set R with two BINARY OPERATIONS [I.2 §2.4], denoted by “+” and “×”, which satisfies all the field axioms apart from the one that says that nonzero elements have multiplicative inverses.
Although the integers are the prototypical example of a ring, the notion arose historically as an abstraction from several sources, one of which was polynomials. Like integers, polynomials (with real coefficients, say) can be added and multiplied, and these operations have all the properties one might expect, such as the fact that multiplication is distributive over addition, so the space of such polynomials forms a ring. Other examples include the integers modulo n (for any positive integer n), the rationals (or indeed any other field), and the set 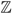 [i] of all complex numbers a + bi such that a and b are integers.
[i] of all complex numbers a + bi such that a and b are integers.
Sometimes the assumptions that multiplication is commutative and has an identity element are dropped. This leads to a more complicated theory, but it does encompass important examples such as the set of all n × n matrices (with elements in a given field, or even just a ring).
As with other algebraic structures, there are several ways of forming new rings from old ones: for instance, we can take subrings and direct products of two rings. Slightly less obviously, we can start with a ring R and form the ring of all polynomials with coefficients in R. We can also take QUOTIENTS [I.3 §3.3], but in order to discuss these we must introduce the notion of an ideal.
2 Ideals
A typical quotient construction for an algebraic structure A will identify some substructure B and regard two elements of A as “equivalent if they “differ by an element of B.” If A is a group or a VECTOR SPACE [I.3 §2.3], then B will be a subgroup or a subspace. However, the situation for rings is slightly different.
We can see why if we think about quotients in another way: as images of HOMOMORPHISMS [I.3 §4.1]. The substructures that we like to quotient by are the kernels of these homomorphisms, so we should ask ourselves what the kernel of a ring homomorphism (that is, the set of elements that map to 0) will be like.
If  : R → R′ is a homomorphism between two rings, and
: R → R′ is a homomorphism between two rings, and  (a) =
(a) =  (b) = 0, then
(b) = 0, then  (a + b) = 0. Also, if r is any element of R, then
(a + b) = 0. Also, if r is any element of R, then  (ra) =
(ra) =  (r)
(r) (a) = 0. Thus, the kernel of a homomorphism is closed under addition, and also under multiplication by any element of the ring. These two properties define the notion of an ideal. For example, the set of all even integers is an ideal in
(a) = 0. Thus, the kernel of a homomorphism is closed under addition, and also under multiplication by any element of the ring. These two properties define the notion of an ideal. For example, the set of all even integers is an ideal in 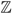 . In interesting cases, ideals are not subrings, since if an ideal contains 1 then it must contain r for every r in the ring. (An example that makes the difference very clear is the subset of the ring of all polynomials that consists of all constant polynomials. The constants form a subring, but they certainly do not form an ideal.)
. In interesting cases, ideals are not subrings, since if an ideal contains 1 then it must contain r for every r in the ring. (An example that makes the difference very clear is the subset of the ring of all polynomials that consists of all constant polynomials. The constants form a subring, but they certainly do not form an ideal.)
It is not hard to show that for any ideal I in a ring R there is a homomorphism that has I as its kernel, namely the quotient map from R to the quotient R/I. Here R/I is a construction that as usual we think of as “R, but with two elements considered the same if they differ by an element of I.”
Quotients of rings are extremely useful in ALGEBRAIC NUMBER THEORY [IV.1] because they allow us to rephrase questions about algebraic numbers as questions about polynomials. To get an idea of how this is done, consider the ring 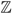 [X] of all polynomials with integer coefficients, and the ideal that consists of all multiples (by integer polynomials) of the polynomial X2 + 1. In the quotient of
[X] of all polynomials with integer coefficients, and the ideal that consists of all multiples (by integer polynomials) of the polynomial X2 + 1. In the quotient of 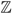 [X] by this ideal, we regard two polynomials as the same if they differ by a multiple of X2 + 1. In particular, X2 is the same as -1. In other words, in this quotient ring we have a square root of -1, and in fact the quotient ring is isomorphic to the ring
[X] by this ideal, we regard two polynomials as the same if they differ by a multiple of X2 + 1. In particular, X2 is the same as -1. In other words, in this quotient ring we have a square root of -1, and in fact the quotient ring is isomorphic to the ring 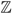 [i] that we met earlier.
[i] that we met earlier.
One of the things we like to do to integers is factorize them, and we can try to do the same in rings as well. However, it turns out that, while it is usually possible to factorize an element of a ring into “irreducible” ones that cannot be factorized further (like the primes in 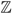 ), in many cases the factorization is not unique. At first, this might be rather unexpected, and indeed it was a stumbling block for many early workers (in the eighteenth and nineteenth centuries). Here is an example: in the ring
), in many cases the factorization is not unique. At first, this might be rather unexpected, and indeed it was a stumbling block for many early workers (in the eighteenth and nineteenth centuries). Here is an example: in the ring 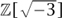 , which consists of all complex numbers a + b
, which consists of all complex numbers a + b , where a and b are integers, the number 4 may be factorized as 2 × 2 and also as
, where a and b are integers, the number 4 may be factorized as 2 × 2 and also as  .
.
3 Modules
Modules are to rings as vector spaces are to fields. In other words, they are algebraic structures where the basic operations are addition and scalar multiplication, but now the scalars are allowed to come from a ring rather than a field. For an example of a module over a ring that is not a field, take any Abelian group G. This can be turned into a module over 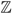 , with addition given by the group operation and scalar multiplication defined in the obvious way: for instance, 3g means g + g + g, and -2g means the inverse of g + g.
, with addition given by the group operation and scalar multiplication defined in the obvious way: for instance, 3g means g + g + g, and -2g means the inverse of g + g.
The simplicity of this definition masks the fact that the structure of modules is in general far more subtle than that of vector spaces. For example, we can define a basis of a module to be a linearly independent set of elements that spans the module. However, many useful facts about bases in vector spaces do not hold for modules. For instance, in 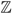 , which we may consider as a module over itself, the set {2, 3} spans the module but does not contain a basis, and similarly the set {2} is linearly independent but cannot be extended to a basis. In fact, modules may be very far from having a basis: for example, if we consider the integers modulo n as a module over
, which we may consider as a module over itself, the set {2, 3} spans the module but does not contain a basis, and similarly the set {2} is linearly independent but cannot be extended to a basis. In fact, modules may be very far from having a basis: for example, if we consider the integers modulo n as a module over 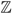 , then even a single element x fails to be linearly independent, since nx = 0.
, then even a single element x fails to be linearly independent, since nx = 0.
The following example of a module is an important one. Let V be a complex vector space and let α be a linear map from V to V. This can be made into a module over the ring  [X]: if υ ∈ V and P is a complex polynomial, then Pυ is defined to be P(α)υ. (For instance, if P is the polynomial x2 + 1, then Pυ = α2υ + υ.) Applying general structural results about modules to this example, one obtains a proof of the JORDAN NORMAL FORM THEOREM [III.43].
[X]: if υ ∈ V and P is a complex polynomial, then Pυ is defined to be P(α)υ. (For instance, if P is the polynomial x2 + 1, then Pυ = α2υ + υ.) Applying general structural results about modules to this example, one obtains a proof of the JORDAN NORMAL FORM THEOREM [III.43].
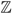 of all integers forms a ring and the set ℚ of all rational numbers forms a field. In general, a ring is a set R with two BINARY OPERATIONS [I.2 §2.4], denoted by “+” and “×”, which satisfies all the field axioms apart from the one that says that nonzero elements have multiplicative inverses.
of all integers forms a ring and the set ℚ of all rational numbers forms a field. In general, a ring is a set R with two BINARY OPERATIONS [I.2 §2.4], denoted by “+” and “×”, which satisfies all the field axioms apart from the one that says that nonzero elements have multiplicative inverses. : R → R′ is a homomorphism between two rings, and
: R → R′ is a homomorphism between two rings, and 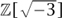 , which consists of all complex numbers a + b
, which consists of all complex numbers a + b , where a and b are integers, the number 4 may be factorized as 2 × 2 and also as
, where a and b are integers, the number 4 may be factorized as 2 × 2 and also as  .
. [X]: if υ ∈ V and P is a complex polynomial, then Pυ is defined to be P(α)υ. (For instance, if P is the polynomial x2 + 1, then Pυ = α2υ + υ.) Applying general structural results about modules to this example, one obtains a proof of the JORDAN NORMAL FORM THEOREM [III.43].
[X]: if υ ∈ V and P is a complex polynomial, then Pυ is defined to be P(α)υ. (For instance, if P is the polynomial x2 + 1, then Pυ = α2υ + υ.) Applying general structural results about modules to this example, one obtains a proof of the JORDAN NORMAL FORM THEOREM [III.43].