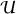of subsets of X (called the “open sets”) satisfying the following axioms.A topological space is the most basic context in which one can understand the notion of a CONTINUOUS FUNCTION [I.3 §5.2].
Let us recall a standard definition of what it means for a function f : ℝ → ℝ to be continuous. Suppose that f (x) = y. Then f is continuous at x provided that f (x′) is close to y whenever x′ is close to x. Of course, to make this a mathematically rigorous notion we have to be precise about the meaning of “close.” We could say that f (x′) is close to y if | f (x′) – f (x)| < ε, where ε > 0 is some small positive constant. And we could deem x to be close to x′ whenever |x – x′| < δ, where δ is another positive constant.
We say that f is continuous at x if an appropriate δ can be found, regardless of how small ε was chosen to be (δ is allowed, of course, to depend on ε). And f is said to be continuous if it is continuous at every point x on the real line.
How might we generalize this notion, replacing ℝ by an arbitrary set X? Our existing definition makes sense only if we can decide when two points x, x′ ∈ X are close. For a general set, which might not be nicely embedded in Euclidean space, this is impossible without the addition of further structure. (When such structure is added one has the notion of a METRIC SPACE [III.56]: metric spaces are less general than topological spaces.)
If the notion of closeness is unavailable, how should one define continuity? The answer may be found in the notion of an open set. A set U ⊂ ℝ is said to be open if for any point x in U there is an interval (a, b) that contains x (that is, a < x < b) and is contained in U.
It is an amusing exercise to check that if f : ℝ → ℝ is continuous, and if U is open, then f-1 (U) is open. Conversely, if f-1 (U) is open for every open set U, then f is continuous. Thus, at least for functions from ℝ to ℝ, one may characterize continuity purely in terms of open sets. The notion of closeness is used only when it comes to defining what an open set is.
We now turn to the formal definition. A topological space is a set X together with a collection 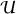of subsets of X (called the “open sets”) satisfying the following axioms.
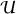is closed under taking arbitrary unions (so if (Ui) i ∈ I is a collection of open sets, then so is Ui∈I Ui). 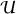is closed under taking finite intersections (so if Ul, . . . , Uk are open sets, then so is U1 ∩ · · · ∩ Uk).The collection 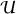is called a topology on X. It is easy to verify that the usual open subsets of ℝ satisfy the above axioms: thus, ℝ forms a topological space with these sets.
A subset of a topological space is called closed if and only if its complement is open. Note that “closed” does not mean “not open”: for example, in the space ℝ, the half-open interval [0, 1) is neither open nor closed, and the empty set is both open and closed.
Note that we do not demand many properties from our open sets: this makes the notion of topological space a rather general one. Indeed, under many circumstances the concept is a little too general: then it can be convenient to assume that a topological space has further properties. For instance, a topological space X is called Hausdorff if, for any two distinct points x1 and x2 in X, there are disjoint open sets U1 and U2 that contain x1 and x2, respectively. Hausdorff topological spaces (of which ℝ is an obvious example) have many useful properties that general topological spaces do not necessarily have.
We saw earlier that for functions from ℝ to ℝ the notion of continuity could be formulated entirely in terms of open sets. This means that we can define continuity for functions between topological spaces: if X and Y are two topological spaces and if f : X → Y is a function between them, then we simply define f to be continuous if f-1 (U) is open for every open set U ⊂ Y. Remarkably, we have found a useful definition of continuity that does not rely on a notion of distance.
A continuous map that has a continuous inverse is known as a homeomorphism. If there is a homeomorphism between two spaces X and Y, then they are regarded as equivalent from the point of view of topology. In topology texts one will often see it said that a topologist is unable to distinguish between a doughnut and a teacup because each can be continuously deformed into the other (imagine that they are both made of modeling clay).
If X is a topological space, then a very useful way of describing the topology on X is by giving a basis for it. This is a subcollection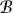 
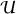⊆ with the property that every open set (that is, every element of 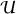) is a union of open sets in 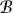. A basis for ℝ with the usual topology is the collection of open intervals {(a, b) : a < b}, and a basis for ℝ2 is the collection of open balls: that is, sets of the form {Bδ(x) = {y: |x - y| <δ}}.
Let us give some examples.
The discrete topology. Let X be any set whatsoever, and take 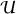to be the collection of all subsets of X. It is a simple matter to check that the axioms for a topological space are satisfied.
Euclidean spaces. Let X = ℝd, and let 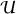contain all sets that are open in the Euclidean metric. That is, U ⊆ X is open if, for every u ∈ U, there is δ > 0 such that Bδ(u) is contained in U. It is only slightly more taxing to check that the axioms are satisfied in this case. More generally, for any metric space the open sets can be defined in a similar way and they form a topological space.
Subspace topology. If X is a topological space and if S ⊆ X, then we may make S a topological space. We declare the open sets in S to be all sets of the form S ∩ U, where U ∈ 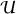is an open set in X.
The Zariski topology. This is used in ALGEBRAIC GEOMETRY [IV.4]. It is specified by giving its closed sets (and hence, by complementation, its open sets)—these are the zero loci of systems of polynomial equations. On ℂ2, for example, these closed sets are precisely the sets of the form
{(z1,z2) : f1 (z1,z2) = f2(z1,z2) = ··· = fk(z1,z2) = 0},
where f1, . . . , fk are polynomials. To show that this defines a topology is somewhat nontrivial, the difficulty being to show that an arbitrary intersection of closed sets is closed (which is equivalent to the assertion that an arbitrary union of open sets is open). This is a consequence of Hilbert’s basis theorem.
The notion of topological space is a very good example of the power of abstraction in mathematics. The definition is simple and covers a wide variety of natural situations, yet it has enough content that one can make interesting definitions and prove theorems purely within the world of topological spaces. It is often fun to take a familiar concept, that applies to ℝ or ℝ2, say, and try to find an analogue of it in the world of general topological spaces. We give two examples.
Connectedness. The rough idea of connectedness is that a connected set is one that does not break up into pieces in an obvious way. Most people would imagine that they could discern, from a list of pictures of reasonably sensible subsets of ℝ2, which were connected and which were not. But can one give a precise mathematical definition that applies to all sets, including potentially very wild ones, and says whether they are connected or not? For example, is the space
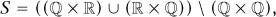
which consists of all points with exactly one rational coordinate, connected or not (with the subspace topology)? It turns out that a definition can indeed be given, and moreover that it applies not just to ℝ2 but to general topological spaces. We say that a space X is connected if there is no decomposition X = U1∪ U2 of X into two disjoint, nonempty, open sets. We leave it to the reader to decide whether S is connected or not.
Compactness. This is one of the most important concepts in all of mathematics, but it can appear strange at first sight. It comes from attempting to abstract the notion of a closed and bounded set (in ℝ2, say) to a general topological space. We say that X is compact if, given any collection C of open sets U that cover X (i.e., whose union is X), we may find a finite subcollection {U1, . . . , Uk} ⊆ C that still covers X. Specializing this definition to ℝ2 with the usual topology, it can indeed be proved that a set S ⊆ ℝ 2 is compact (in the subspace topology) if and only if it is closed and bounded. See COMPACTNESS AND COMPACTIFICATION [III.9] for more information.