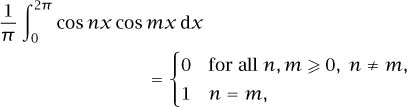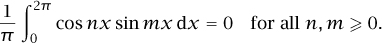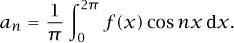III.92 Trigonometric Functions
Ben Green
The basic trigonometric functions “sin” and “cos,” as well as the four related functions “tan,” “cot,” “sec,” and “cosec,” will probably be familiar to most readers in some form. One way to define the sine function sin : ℝ → [-1, 1] is as follows.
In almost all branches of mathematics one measures angles using radians, which are defined in terms of arc-length: to say that the angle  AOB in figure 1 is θ radians is to say that the arc AB of the circle has length θ. This definition makes sense when 0 ≤ θ < 2π. One then defines sin θ to be the length PB, where P is the foot of the perpendicular from B to OA. It is very important that this length be taken with the correct sign. If 0 < θ θ < π then we take the positive sign, whereas if π < θ < 2π we take the negative sign. In other words, sin θ is the y-coordinate of the point B.
AOB in figure 1 is θ radians is to say that the arc AB of the circle has length θ. This definition makes sense when 0 ≤ θ < 2π. One then defines sin θ to be the length PB, where P is the foot of the perpendicular from B to OA. It is very important that this length be taken with the correct sign. If 0 < θ θ < π then we take the positive sign, whereas if π < θ < 2π we take the negative sign. In other words, sin θ is the y-coordinate of the point B.
The sine function is, at the moment, defined on the interval [0, 2π). To define it on all of ℝ one simply insists that it be periodic with period 2π (that is, that it satisfies the relation sin θ = sin(2πn + θ) for any integer n).
There is one problem with our definition of sine. What do we mean by the length of the arc AB? The only really satisfactory way of understanding this is to use calculus. The equation of the unit circle is 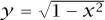 at least if (x,y) lies in the upper-right quadrant. (Otherwise one must be careful about sign.) The formula for the arc-length of a curve y = f (x) between y = a and y = b is
at least if (x,y) lies in the upper-right quadrant. (Otherwise one must be careful about sign.) The formula for the arc-length of a curve y = f (x) between y = a and y = b is

(This may be thought of as a definition, though the motivation for the definition comes from pictures.) For the circle,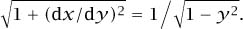 Since the arc-length of the circle between the points P = (x, sin θ)
Since the arc-length of the circle between the points P = (x, sin θ)

Figure 1 Interpreting trigonometric functions geometrically.
and A = (1,0) is θ, this gives the formula
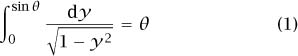
for 0 ≤ θ ≤ π/2 (we do not care about what x is). This can be regarded as giving a precise, even if implicit, definition of sin θ for 0 ≤ θ ≤ π/2.
As with many of the most natural concepts in mathematics, sin may be defined in a multitude of equivalent ways. Another definition (whose equivalence to the first one is not obvious) is
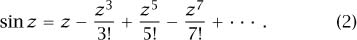
This infinite series converges for all real z. The resulting definition has a distinct advantage over (1), in that it also makes sense when z is an arbitrary complex number (that is why we replaced the letter θ by z). It therefore allows us to extend sin to a HOLOMORPHIC FUNCTION [I.3 § 5.6] On ℂ.
If the sine function is analytic, then what is its derivative? The answer is the cosine function cos z, which may be defined in much the same way as sin: either geometrically or using a power series. The power series is

which may be obtained by differentiating the series for sin term by term (naturally, this is an operation that must be properly justified, but it can be).
If one differentiates again, one gets the formula (d2/dz2) sin z = – sin z. In fact, it is possible to define sin : ℝ → [–1, 1] as the unique solution y to the differential equation y” = -y that also satisfies the initial value conditions y (0) = 0, y′ (0) = 1. This is a very sensible way of proving that the two definitions (1) and(2) are equivalent (it is a good calculus exercise to prove that sin” = –sin using (1)).
Ultimately, the power series expansions (2) and (3) display the most important side of sin and cos, which is their relation with the EXPONENTIAL FUNCTION [III.25]:
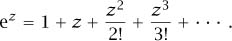
Comparing this with (2) and (3), one gets the famous formula
eiθ = cos θ + i sin θ.
The exponential functions θ 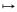 einθ are characters, that is, HOMOMORPHISMS [I.3 §4.1] from ℝ/2πℤ to the unit circle S1 (which form groups under addition mod 2π and multiplication, respectively). This makes them the natural objects with which to do a FOURIER ANALYSIS [III.27] of 2π-periodic functions on ℝ. Because sin and cos are real-valued, it is convenient to try to decompose such a function f (x) not into exponentials, but as a series
einθ are characters, that is, HOMOMORPHISMS [I.3 §4.1] from ℝ/2πℤ to the unit circle S1 (which form groups under addition mod 2π and multiplication, respectively). This makes them the natural objects with which to do a FOURIER ANALYSIS [III.27] of 2π-periodic functions on ℝ. Because sin and cos are real-valued, it is convenient to try to decompose such a function f (x) not into exponentials, but as a series
a0 + a1 cos x + b1 sin x + a2 cos 2x + b2 sin 2x + ··· .
Under favorable circumstances (if the function f is sufficiently smooth, say) one can recover the coefficients ai, bi by using orthogonality relations such as
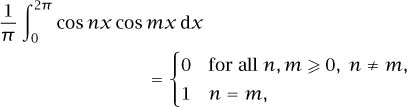
and
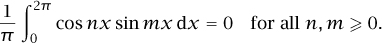
Thus, for example, we have
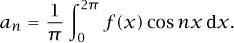
Such decompositions into trigonometric functions ultimately underlie devices like compact disk players and mobile phones.
Let us conclude by remarking that there is a whole zoo of formulas concerning sin, cos, and the other four trigonometric functions (which we have not discussed here), as well as integrals involving these functions. It is these formulas that make the trigonometric functions an indispensable tool in classical Euclidean geometry. There are many further formulas in that setting. To mention just one beautiful example, the area of a triangle inscribed in a unit circle with angles A, B, and C is exactly 2 sinA sinB sinC.
Uncountable Sets
See COUNTABLE AND UNCOUNTABLE SETS [III.11]
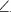 AOB in figure 1 is θ radians is to say that the arc AB of the circle has length θ. This definition makes sense when 0 ≤ θ < 2π. One then defines sin θ to be the length PB, where P is the foot of the perpendicular from B to OA. It is very important that this length be taken with the correct sign. If 0 < θ θ < π then we take the positive sign, whereas if π < θ < 2π we take the negative sign. In other words, sin θ is the y-coordinate of the point B.
AOB in figure 1 is θ radians is to say that the arc AB of the circle has length θ. This definition makes sense when 0 ≤ θ < 2π. One then defines sin θ to be the length PB, where P is the foot of the perpendicular from B to OA. It is very important that this length be taken with the correct sign. If 0 < θ θ < π then we take the positive sign, whereas if π < θ < 2π we take the negative sign. In other words, sin θ is the y-coordinate of the point B.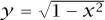 at least if (x,y) lies in the upper-right quadrant. (Otherwise one must be careful about sign.) The formula for the arc-length of a curve y = f (x) between y = a and y = b is
at least if (x,y) lies in the upper-right quadrant. (Otherwise one must be careful about sign.) The formula for the arc-length of a curve y = f (x) between y = a and y = b is
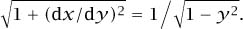 Since the arc-length of the circle between the points P = (x, sin θ)
Since the arc-length of the circle between the points P = (x, sin θ)
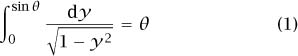
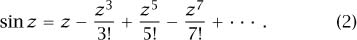

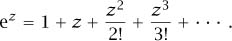
 einθ are characters, that is, HOMOMORPHISMS [I.3 §4.1] from ℝ/2πℤ to the unit circle S1 (which form groups under addition mod 2π and multiplication, respectively). This makes them the natural objects with which to do a FOURIER ANALYSIS [III.27] of 2π-periodic functions on ℝ. Because sin and cos are real-valued, it is convenient to try to decompose such a function f (x) not into exponentials, but as a series
einθ are characters, that is, HOMOMORPHISMS [I.3 §4.1] from ℝ/2πℤ to the unit circle S1 (which form groups under addition mod 2π and multiplication, respectively). This makes them the natural objects with which to do a FOURIER ANALYSIS [III.27] of 2π-periodic functions on ℝ. Because sin and cos are real-valued, it is convenient to try to decompose such a function f (x) not into exponentials, but as a series