Our goal is to sketch some of the essential ideas of arithmetic geometry; we begin with a problem which, on the face of it, involves no geometry and only a bit of arithmetic.
Problem. Show that the equation
has no solution in nonzero rational numbers x, y, z.
(Note that it is only in the coefficient 7 that (1) differs from the Pythagorean equation x2 + y2 = z2, which we know has infinitely many solutions. It is a feature of arithmetic geometry that modest changes of this kind can have drastic effects!)
Solution. Suppose x, y, z are rational numbers satisfying (1); we will derive from this a contradiction.
If n is the least common denominator of x, y, z, we can write
x = a/n, y = b/n, z = c/n
such that a, b, c, and n are integers. Our original equation (1) now becomes
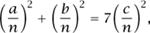
and multiplying through by n2 one has
If a, b, and c have a common factor m, then we can replace them by a/m, b/m, and c/m, and (2) still holds for these new numbers. We may therefore suppose that a, b, and c are integers with no common factor.
We now reduce the above equation modulo 7 (see MODULAR ARITHMETIC [III.58]). Denote by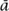 
and 
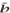the reductions of a and b modulo 7. The right-hand side of (2) is a multiple of 7, so it reduces to 0. We are left with
Now there are only seven possibilities for 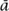, and seven possibilities for 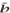. So the analysis of the solutions of (3) amounts to checking the forty-nine choices of 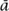, 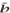and seeing which ones satisfy the equation. A few minutes of calculation are enough to convince us that (3) is satisfied only if 
.
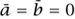But saying that 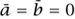is the same as saying that a and b are both multiples of 7. This being the case, a2 and b2 are both multiples of 49. It follows that their sum, 7c2, is a multiple of 49 as well. Therefore, c2 is a multiple of 7, and this implies that c itself is a multiple of 7. In particular, a, b, and c share a common factor of 7. We have now arrived at the desired contradiction, since we chose a, b, and c to have no common factor. Thus, the hypothesized solution leads us to a contradiction, so we are forced to conclude that there is not, in fact, any solution to (1) consisting of nonzero rational numbers.1
In general, the determination of rational solutions to a polynomial equation like (2) is called a Diophantine problem. We were able to dispose of (2) in a paragraph, but that turns out to be the exception: in general, Diophantine problems can be extraordinarily difficult. For instance, we might modify the exponents in (2) and consider the equation
I do not know whether (4) has any solutions in nonzero rational numbers or not; one can be sure, though, that determining the answer would be a substantial piece of work, and it is quite possible that the most powerful techniques available to us are insufficient to answer this simple question.
More generally, one can take an arbitrary commutative RING [III.81] R, and ask whether a certain polynomial equation has solutions in R. For instance, does (2) have a solution with x, y, z in the polynomial ring ℂ[t]? (The answer is yes. We leave it as an exercise to find some solutions.) We call the problem of solving a polynomial equation over R a Diophcrntine problem over R. The subject of arithmetic geometry has no precise boundary, but to a first approximation one may say that it concerns the solution of Diophantine problems Over subrings Of NUMBER FIELDS [III.63]. (TO be honest, a problem is usually called Diophantine only when R is a subring of a number field. However, the more general definition suits our current purposes.)
With any particular equation like (2), one can associate infinitely many Diophantine problems, one for each commutative ring R. A central insight—in some sense the basic insight—of modern algebraic geometry is that this whole gigantic ensemble of problems can be treated as a single entity. This widening of scope reveals structure that is invisible if we consider each problem on its own. The aggregate we make of all these Diophantine problems is called a scheme. We will return to schemes later, and will try, without giving precise definitions, to convey some sense of what is meant by this not very suggestive term.
A word of apology: I will give only the barest sketch of the immense progress that has taken place in arithmetic geometry in recent decades—there is simply too much to cover in an article of the present scope. I have chosen instead to discuss at some length the idea of a scheme, assuming, I hope, minimal technical knowledge on the part of the reader. In the final section, I shall discuss some outstanding problems in arithmetic geometry with the help of the ideas developed in the body of the article. It must be conceded that the theory of schemes, developed by Grothendieck and his collaborators in the 1960s, belongs to algebraic geometry as a whole, and not to arithmetic geometry alone. I think, though, that in the arithmetic setting, the use of schemes, and the concomitant extension of geometric ideas to contexts that seem “nongeometric” at first glance, is particularly central.
Before we dive into the abstract theory of schemes, let us splash around a little longer among the polynomial equations of degree 2. Though it is not obvious from our discussion so far, the solution of Diophantine problems is properly classified as part of geometry. Our goal here will be to explain why this is so.
Suppose we consider the equation
One can ask: which values of x, y ∈ ℚ satisfy (5)? This problem has a flavor very different from that of the previous section. There we looked at an equation with no rational solutions. We shall see in a moment that (5), by contrast, has infinitely many rational solutions. The solutions x = 0, y = 1 and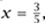 
are representative examples. (The four solutions (±1, 0) and (0, ±1) are the ones that would be said, in the usual mathematical parlance, to be “staring you in the face.”)
Equation (5) is, of course, immediately recognizable as “the equation of a circle.” What, precisely, do we mean by that assertion? We mean that the set of pairs of real numbers (x, y) satisfying (5) forms a circle when plotted in the Cartesian plane.
So geometry, as usually construed, makes its entrance in the figure of the circle. Now suppose that we want to find more solutions to (5). One way to proceed is as follows. Let P be the point (1, 0), and let L be a line through P of slope m. Then we have the following geometric fact.
(G) The intersection of a line with a circle consists of either zero, one, or two points; the case of a single point occurs only when the line is tangent to the circle.
From (G) we conclude that, unless L is the tangent line to the circle at P, there is exactly one point other than P where the line intersects the circle. In order to find solutions (x, y) to (5), we must determine coordinates for this point. So suppose L is the line through (1, 0) with slope m, which is to say it is the line Lm whose equation is y = m(x - 1). Then in order to find the x-coordinates of the points of intersection between Lm and the circle, we need to solve the simultaneous equations y = m(x - 1) and x2 + y2 = 1; that is, we need to solve x2 + m2 (x - 1)2 = 1 or, equivalently,
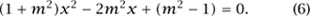
Of course, (6) has the solution x = 1. How many other solutions are there? The geometric argument above leads us to believe that there is at most one solution to (6). Alternatively, we can use the following algebraic fact, which is analogous2 to the geometric fact (G).
(A) The equation (1 + m2) x2 - 2m2x + (m2 - 1) = 0 has either zero, one, or two solutions in x.
Of course, the conclusion of statement (A) holds for any nontrivial quadratic equation in x, not just (6); it is a consequence of the factor theorem.
In this case, it is not really necessary to appeal to any theorem; one can find by direct computation that the solutions of (6) are x = 1 and x = (m2 - 1)/(m2 + 1). We conclude that the intersection between the unit circle and Lm consists of (1, 0) and the point Pm with coordinates
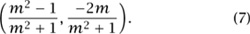
Equation (7) establishes a correspondence m 
Pm, which associates with each slope m a solution Pm to (5). What is more, since every point on the circle, other than (1, 0) itself, is joined to (1, 0) by a unique line, we find that we have established a one-to-one correspondence between slopes m and solutions, other than (1, 0), to equation (5).
A very nice feature of this construction is that it allows us to construct solutions to (5) not only over 
but over smaller fields, like 
: it is evident that, when m is rational, so are the coordinates of the solution yielded by (7). For example, taking m = 2 yields the solution 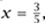. In fact, not only does (7) show us that (5) admits infinitely many solutions over , it also gives us an explicit way to parametrize the solutions in terms of a variable m. We leave it as an exercise to prove that the solutions of (5) over , apart from (1, 0), are in one-to-one correspondence with rational values of m. Alas, rare is the Diophantine problem whose solutions can be parametrized in this way! Still, polynomial equations like (5) with solutions that can be parametrized by one or more variables play a special role in arithmetic geometry; they are called rational varieties and constitute by any measure the best-understood class of examples in the subject.
I want to draw your attention to one essential feature of this discussion. We relied on geometric intuition (e.g., our knowledge of facts like (G)) to give us ideas about how to construct solutions to (5). On the other hand, now that we have erected an algebraic justification for our construction, we can kick away our geometric intuition as needless scaffolding. It was a geometric fact about lines and circles that suggested to us that (6) should have only one solution other than x = 1. However, once one has had that thought, one can prove that there is at most one such solution by means of the purely algebraic statement (A), which involves no geometry whatsoever.
The fact that our argument can stand without any reference to geometry means that it can be applied in situations that might not, at first glance, seem geometric. For instance, suppose we wished to study solutions to (5) over the finite field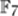 
. Now this solution set would not seem rightfully to be called “a circle” at all—it is just a finite set of points! Nonetheless, our geometrically inspired argument still works perfectly. The possible values of m in 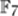are 0, 1, 2, 3, 4, 5, 6, and the corresponding solutions Pm are (-1, 0), (0, -1), (2, 2), (5, 5), (5, 2), (2, 5), (0, 1). These seven points, together with (1, 0), form the whole solution set of (5) over .
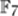We have now started to reap the benefits of considering a whole bundle of Diophantine problems at once; in order to find the solutions to (5) over 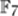, we used a method that was inspired by the problem of finding solutions to (5) over . Similarly, in general, methods suggested by geometry can help us solve Diophantine problems. And these methods, once translated into purely algebraic form, still apply in situations that do not appear to be geometric.
We must now open our minds to the possibility that the purely algebraic appearance of certain equations is deceptive. Perhaps there could be a sense of “geometry” that was general enough to include entities like the solution set of (5) over 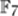, and in which this particular example had every right to be called a “circle.” And why not? It has properties a circle has: most importantly for us, it has either zero, one, or two intersection points with any line. Of course, there are features of “circleness” which this set of points lacks: infinitude, continuity, roundness, etc. But these latter qualities turn out to be inessential when we are doing arithmetic geometry. From our viewpoint the set of solutions of (5) over 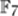has every right to be called the unit circle.
To sum up, you might think of the modern point of view as an upending of the traditional story of Cartesian space. There, we have geometric objects (curves, lines, points, surfaces) and we ask questions such as, “What is the equation of this curve?” or “What are the coordinates of that point?” The underlying object is the geometric one, and the algebra is there to tell us about its properties. For us, the situation is exactly reversed: the underlying object is the equation, and the various geometric properties of solution sets of the equation are merely tools that tell us about the equation’s algebraic properties. For an arithmetic geometer, “the unit circle” is the equation x2 + y2 = 1. And the round thing on the page? That is just a picture of the solutions to the equation over . It is a distinction that makes a remarkable difference.
In this section, we will attempt to give a clearer answer to the question, “What is a scheme?” Instead of trying to lay out a precise definition—which requires more algebraic apparatus than would fit comfortably here—we will approach the question by means of an analogy.
So let us think about adjectives. Any adjective, such as “yellow” for instance, picks out a set of nouns to which the adjective applies. For each adjective A, we might call this set of nouns Γ(A). For instance, Γ(“yellow”) is an infinite set that might look like {lemon, school bus, banana, sun, . . .}.3 And anyone would agree that Γ(A) is an important thing to know about A.
Now suppose that, moved by a desire for lexical parsimony, a theoretician among us suggested that adjectives could in fact be dispensed with entirely. If, instead of A, we spoke only of Γ(A), we could get by with a grammatical theory involving only nouns.
Is this a good idea? Well, there are certainly some obvious ways that things could go wrong. For instance, what if lots of different adjectives were sent to the same set of nouns? Then our new viewpoint would be less precise than the old one. But it certainly seems that if two adjectives apply to exactly the same set of nouns, then it is fair to say that the adjectives are the same, or at least synonymous.
What about relationships between adjectives? For instance, we can ask of two adjectives whether one is stronger than another, in the way that “gigantic” is stronger than “large.” Is this relationship between adjectives still visible on the level of sets of nouns? The answer is yes: it seems fair to say that A is “stronger than” B precisely when Γ (A) is a subset of Γ(B). In other words, what it means to say that “gigantic” is stronger than “large” is that all gigantic things are large, though some large things may not be gigantic.
So far, so good. We have paid a price in technical difficulty: it is much more cumbersome to speak of infinite sets of nouns than it was to use simple, familiar adjectives. But we have gained something, too: the opportunity for generalization. Our theoretician—whom we may now call a “set-theoretic grammarian”—observes that there is, perhaps, nothing special about the sets of nouns that happen to be of the form Γ(A) for some already known adjective A. Why not take a conceptual leap and redefine the word “adjective” to mean “a set of nouns”? To avoid confusion with the usual meaning of “adjective,” the theoretician might even use a new term, like “quality,” to refer to his new objects of study.
Now we have a whole new world of qualities to play with. For example, there is a quality {“school bus”, “sun”} which is stronger than “yellow,” and a quality {“sun”} (not the same thing as the noun “sun”!) which is stronger than the qualities “yellow,” “gigantic,” “large,” and {“school bus”, “sun”}.
I may not have convinced you that, on balance, this reconception of the notion of “adjective” is a good idea. In fact, it probably is not, which is why set-theoretic grammar is not a going concern. The corresponding story in algebraic geometry, however, is quite a different matter.
A warning: the next couple of sections will be difficult going for those not familiar with rings and ideals—such readers can either skip to section 4, or try to follow the discussion after reading RINGS, IDEALS, AND MODULES [III.81] (see also ALGEBRAIC NUMBERS [IV.1]).
Let us recall that a complex afffine variety (from now on, just “variety”) is the set of solutions over 
to some finite set of polynomial equations. For instance, one variety V we could define is the set of points (x,y) in 2 satisfying our favorite equation
Then V is what we called in the previous section “the unit circle,” though in fact the shape of the set of complex solutions of (8) is a sphere with two points removed. (This is not supposed to be obvious.) It is a question of general interest, given some variety X, to understand the ring of polynomial functions that take points on X to complex numbers. This ring is called the coordinate ring of X, and is denoted Γ (X).
Certainly, given any polynomial in x and y, we can regard it as a function defined on our particular variety V. So is the coordinate ring of V just the polynomial ring [x,y]? Not quite. Consider, for instance, the function f = 2x2 + 2y2 + 5. If we evaluate this function at various points on V,
we notice that f keeps taking the same value; indeed, since x2 + y2 = 1 for all (x,y) ∈ V, we see that f = 2(x2 + y2) + 5 takes the value 7 at every point on V. So 2x2 + 2y2 + 5 and 7 are just different names for the same function on V.
So Γ(V) is smaller than [x,y]; it is the ring obtained from [x,y] by declaring two polynomials f and g to be the same function whenever they take the same value at every point of V. (More formally, we are defining an EQUIVALENCE RELATION [I.2 § 2.3] On the set of complex polynomials in two variables.) It turns out that f and g have this property precisely when their difference is a multiple of x2 + y2 - 1. Thus, the ring of polynomial functions on V is the quotient of [x,y] by the ideal generated by x2 + y2 - 1. This ring is denoted by [x,y]/(x2 + y2 - 1).
We have shown how to attach a ring of functions to any variety. It is not hard to show that, if X and Y are two varieties, and if their coordinate rings Γ(X) and Γ(Y) are ISOMORPHIC [I.3 § 4.1], then X and Y are in a sense the “same” variety. It is a short step from this observation to the idea of abandoning the study of varieties entirely in favor of the study of rings. Of course, we are here in the position of the set-theoretic grammarian in the parable above, with “variety” playing the part of “adjective” and “coordinate ring” the part of “set of nouns.”
Happily, we can recover the geometric properties of a variety from the algebraic properties of its coordinate ring; if this were not the case, the coordinate ring would not be such a useful object! The relationship between geometry and algebra is a long story—and much of it belongs to algebraic geometry in general, not arithmetic geometry in particular—but to give the flavor, let us discuss some examples.
A straightforward geometric property of a variety is irreducibility. We say a variety X is reducible if X can be expressed as the union of two varieties X1 and X2, neither of which is the whole of X. For example, the variety
in 2 is the union of the lines x = y and x = -y. A variety is called irreducible if it is not reducible. All varieties are thus built up from irreducible varieties: the relationship between irreducible varieties and general varieties is rather like the relationship between prime numbers and general positive integers.
Moving from geometry to algebra, we recall that a ring R is called an integral domain if, whenever f, g are nonzero elements of R, their product f g is also nonzero; the ring [x,y] is a good example.
Fact. A variety X is irreducible if and only if Γ(X) is an integral domain.
Experts will note that we are glossing over issues of “reducedness” here.
We will not prove this fact, but the following example is illustrative: consider the two functions f = x - y and g = x + y on the variety X defined by (9). Neither of these functions is the zero function; note, for instance, that f (1, -1) is nonzero, as is g(1, 1). Their product, however, is x2 - y2, which is equal to zero on X; so Γ(X) is not an integral domain. Notice that the functions f and g that we chose are closely related to the decomposition of X as the union of two smaller varieties.
Another crucial geometric notion is that of functions from one variety to another. (It is common practice to call such functions “maps” or “morphisms”; we will use the three words interchangeably.) For instance, suppose that W is the variety in 3 determined by the equation xyz = 1. Then the map F: 3 →, 2 defined by
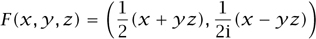
maps points of W to points of V.
It turns out that knowing the coordinate rings of varieties makes it very easy to see the maps between the varieties. We merely observe that if G : V1 → V2 is a map between varieties V1 and V2, and if f is a polynomial function on V2, then we have a polynomial function on V1 that sends every point v to f (G(v)). This function on V1 is denoted by G* (f). For example, if f is the function x + y on V, and F is the map above, F* (f) = 
(x + yz) +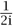 
(x - yz). It is easy to check that G* is a -algebra homomorphism (that is, a homomorphism of rings that sends each element of to itself) from Γ(V2) to Γ(V1). What is more, one has the following theorem.
Fact. For any pair of varieties V, W, the correspondence sending G to G* is a bijection between the polynomial functions sending W to V and the -algebra homomorphisms from Γ(V) to Γ(W).
You would not be far off in thinking of the statement “there is an injective map from V to W” as analogous to “quality A is stronger than quality B.”
The move to transform geometry into algebra is not something one undertakes out of sheer love of abstraction, or hatred of geometry. Instead, it is part of the universal mathematical instinct to unify seemingly disparate theories. I cannot put it any better than Dieudonné (1985) does in his History of Algebraic Geometry:
. . . from [the 1882 memoirs of] Kronecker and Dedekind-Weber dates the awareness of the profound analogies between algebraic geometry and the theory of algebraic numbers, which originated at the same time. Moreover, this conception of algebraic geometry is the most simple and most clear for us, trained as we are in the wielding of “abstract” algebraic notions: rings, ideals, modules, etc. But it is precisely this “abstract” character that repulsed most contemporaries, disconcerted as they were by not being able to recover the corresponding geometric notions easily. Thus the influence of the algebraic school remained very weak up until 1920 . . . . It certainly seems that Kronecker was the first to dream of one vast algebraico-geometric construction comprising these two theories at once; this dream has begun to be realized only recently, in our era, with the theory of schemes.
Let us therefore move on to schemes.
We have seen that each variety X gives rise to a ring Γ(X), and furthermore that the algebraic study of these rings can stand in for the geometric study of varieties. But just as not every set of nouns corresponds to an adjective, not every ring arises as the coordinate ring of a variety. For example, the ring 
of integers is not the coordinate ring of a variety, as we can see by the following argument: for every complex number a and every variety V, the constant function a is a function on V, and therefore ⊂ Γ(V) for every variety V. Since does not contain as a subring, it is not the coordinate ring of any variety.
Now we are ready to imitate the set-theoretic grammarian’s coup de grâce. We know that some, but not all, rings arise from geometric objects (varieties); and we know that the geometry of these varieties is described by algebraic properties of these special rings. Why not, then, just consider every ring R to be a “geometric object” whose geometry is determined by algebraic properties of R? The grammarian needed to invent a new word, “quality,” to describe his generalized adjectives; we are in the same position with our rings-thatare-not-coordinate-rings; we will call them schemes.
So, after all this work, the definition of scheme is rather prosaic—schemes are rings! (In fact, we are hiding some technicalities; it is correct to say that affine schemes are rings. Restricting our attention to affine schemes will not interfere with the phenomena that we are aiming to explain.) More interesting is to ask how we can carry out the task whose difficulty “disconcerted” the early algebraic geometers—how can we identify “geometric” features of arbitrary rings?
For instance, if R is supposed to be an arbitrary geometric object, it ought to have “points.” But what are the “points” of a ring? Clearly we cannot mean by this the elements of the ring; for in the case R = Γ(X), the elements of R are functions on X, not points on X. What we need, given a point p on X, is some entity attached to the ring R that corresponds to p.
The key observation is that we can think of p as a map from Γ(X) to : given a function f from Γ(X) we map it to the complex number f (p). This map is a homomorphism, called the evaluation homomorphism at p. Since points on X give us homomorphisms on Γ(X), a natural way to define the word “point” for the ring R = Γ(X), without using geometry, is to say that a “point” is a homomorphism from R to . It turns out that the kernel of such a homomorphism is a maximal ideal, i.e., a proper ideal in R which is contained in no larger ideal except R itself. Moreover, every maximal ideal of R arises from a point p of X. So a very concise way to describe the points of X might be to say that they are the maximal ideals of R. A modern algebraic geometer would say that all prime ideals correspond to points, not only the maximal ones. The “points” corresponding to the nonmaxímal ideals are not points in the usual sense of the term; for instance, the point corresponding to the zero ideal (when it is prime) is the “generic point,” which is in one sense everywhere on X at once, and in another sense nowhere in particular at all. This description sounds rather woolly, but on the algebraic side the zero ideal is something quite concrete—and in fact, having a precise notion of “generic point” turns out quite often to be useful in making a certain species of vague geometric argument into a rigorous proof.
The definition we have arrived at makes sense for all rings R, and not just those of the form R = Γ(X). So we might define the “points” of a ring R to be its prime ideals. The set of prime ideals of R is given the name Spec R, and it is Spec R that we call the scheme cissociated with R. (More precisely, Spec R is defined to be a “locally ringed topological space” whose points are the prime ideals of R, but we will not need the full power of this definition for our discussion here.)
We are now in a position to elucidate our claim, made in the first section, that a scheme incorporates into one package Diophsntine problems over many different rings. Suppose, for instance, that R is the ring [x,y]/(x2 + y2 - 1). We are going to catalog the homomorphisms f : R → . To specify f, I merely have to tell you the values of f (x) and f (y) in . But I cannot choose these values arbitrarily: since x2 + y2 - 1 = 0 in R, it must be the case that f (x)2 + f (y)2 - 1 = 0 in . In other words, the pair (f (x), f (y)) constitutes a solution over to the Diophantine equation x2 + y2 = 1. What is more, the same argument shows that, for any ring S, a homomorphism f : R → S yields a solution over S to x2 + y2 = 1, and vice versa. In summary,
for each S, there is a one-to-one correspondence between the set of ring homomorphisms from R to S, and solutions over S to x2 + y2 = 1.
This behavior is what we have in mind when we say that the ring R “packages” information about Diophantine equations over different rings.
It turns out, just as one might hope, that every interesting geometric property of varieties can be computed by means of the coordinate ring, which means it can be defined not only for varieties but also for general schemes. We have already seen, for instance, that a variety X is irreducible if and only if Γ(X) is an integral domain. Thus, we say in general that a scheme Spec R is irreducible if and only if R is an integral domain (or, more precisely, if the quotient of R by its nilradical is an integral domain). One can speak of the connectedness of a scheme, its dimension, whether it is smooth, and so forth. All these geometric properties turn out, like irreducibility, to have purely algebraic descriptions. In fact, to the arithmetic geometer’s way of thinking, all these are, at bottom, algebraic properties.
, the Number LineThe first ring we encounter in our mathematical education—and the ring that is the ultimate subject of number theory—is , the ring of integers. How does it fit into our picture? The scheme Spec has as its points the set of prime ideals of , which come in two flavors: there are the principal ideals (p), with p a prime number; and there is the zero ideal.
We are supposed to think of as the ring of “functions” on Spec . How can an integer be a function? Well, I merely need to tell you how to evaluate an integer n at a point of Spec . If the point is a nonzero prime ideal (p), then the evaluation homomorphism at (p) is precisely the homomorphism whose kernel is (p); so the value of n at (p) is just the reduction of n modulo p. At the point (0), the evaluation homomorphism is the identity map → ; so the value of n at (0) is just n.
We now return to the method of section 2, paying particular attention to the case where the equation x2 + y2 = 1 is considered over a finite field 
p.
Let us write V for the scheme of solutions of x2 + y2 = 1. For any ring R, we will denote by V(R) the set of solutions of x2 + y2 = 1.
If R is a finite field p, the set V(p) is a subset of 
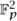. In particular, it is a finite set. So it is natural to wonder how large this set is: in other words, how many points does a circle have?
In section 2, guided by our geometric intuition, we observed that, for every m ∈ , the point
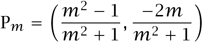
lies on V.
The algebraic computation showing that Pm satisfies the equation x2 + y2 = 1 is no different over a finite field. So we might be inclined to think that V(p) consists of p + 1 points: namely, the points Pm for each m ∈ p, together with (1, 0).
But this is not right: for instance, when p = 5 it is easy to check that the four points (0, 1), (0, -1), (1, 0), (-1, 0) make up all of V(5). Computing Pm for various m, we quickly discover the problem; when m is 2 or 3, the formula for Pm does not make sense, because the denominator m2 + 1 is zero! This is a wrinkle we did not see over , where m2 + 1 was always positive.
What is the geometric story here? Consider the intersection of the line L2, that is, the line y = 2(x - 1), with V. If (x,y) belongs to this intersection, then x2 + (2(x - 1))2 = 1, so 5x2 - 8x + 3 = 0. Since 5 = 0 and 8 = 3 in 5, this equation can be written as 3 - 3x = 0; in other words, x = 1, which in turn implies that y = 0. In other words, the line L2 intersects the circle V at only one point!
We are left with two possibilities, both disturbing to our geometric intuition. We might declare that L2 is tangent to V; but this means that V would have multiple tangents at (1, 0), since the vertical line x = 1 should surely still be considered a tangent. The alternative is to declare that L2 is not tangent to V; but then we are in the equally unsavory situation of having a line which, while not tangent to the circle V, intersects it at only one point. You are now beginning to see why I did not include an algebraic definition of “tangent” in statement (A) above!
This quandary illustrates the nature of arithmetic geometry nicely. When we move into novel contexts, like geometry over p, some features stay fixed (such as “a line intersects a circle in at most two points”), while others have to be discarded (such as “there exists exactly one line, which we may call the tangent line to the circle at (1, 0), that intersects the circle at (1, 0) and no other point”4).
Notwithstanding these subtleties, we are now ready to compute the number of points in V(p). First of all, when p = 2 one can check directly that (0, 1) and (1, 0) are the only two points in V(2). Having treated this case, we assume for the rest of this section that p is odd. It follows from basic number theory that the equation m2 + 1 = 0 has a solution in p if and only if p - 1 (mod 4), in which case there are exactly two such m. So, if p = 3 (mod 4), then every line Lm intersects the circle at a point other than (1, 0), and we have p + 1 points in all. If p = 1 (mod 4), there are two choices of m for which Lm intersects V only at (1, 0); eliminating these two choices of m yields a total of p - 1 points in V(p).
We conclude that |V(p)| is equal to 2 when p = 2, to p - 1 when p ≡ 1 (mod 4), and to p + 1 when p ≡ 3 (mod 4). The interested reader will find the following exercises useful: how many solutions are there to x2 + 3y2 = 1 over p? What about x2 + y2 = 0?
More generally, let X be the scheme of solutions of any system of equations
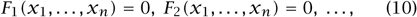
where the Fi are polynomials with integral coefficients. Then one can associate with F a list of integers N2 (X), N3 (X), N5 (X), . . . , where Np (X) is the number of solutions to (10) with x1, . . . , xn ∈ p. This list of integers turns out to contain a surprising amount of geometric information about the scheme X; even for the simplest schemes, the analysis of these lists is a deep problem of intense current interest, as we will see in the next section.
In this section I will try to give an impression of a few of arithmetic geometry’s great successes, and to gesture at some problems of current interest for researchers in the area.
A word of warning is in order. In what follows, I will be trying to give brief and nontechnical descriptions of some mathematics of extreme depth and complexity. Consequently, I will feel very free to oversimplify. I will try to avoid making assertions that are actually false, but I will often use definitions (like that of the L-function attached to an elliptic curve) that do not exactly agree with those in the literature.
The world is not lacking in expositions of the proof of FERMAT’S LAST THEOREM [V.10] and I will not attempt to give another one here, although it is without question the most notable contemporary achievement in arithmetic geometry. (Here I am using the mathematician’s sense of “contemporary,” which, as the old joke goes, means “theorems proved since I entered graduate school.” The shorthand for “theorems proved before I entered graduate school” is “classical.”) I will content myself with making some comments about the structure of the proof, emphasizing connections with the parts of arithmetic geometry we have discussed above.
Fermat’s last theorem (rightly called “Fermat’s conjecture,” since it is almost impossible to imagine that FERMAT [VI.12] proved it) asserts that the equation
where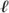 
is an odd prime, has no solutions in positive integers A, B, C.
The proof uses the crucial idea, introduced independently by Frey and Hellegeuarch, of associating with any solution (A, B, C) of (11) a certain variety XA,B, namely the curve described by the equation
y2 = x(x - A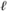
) (x + B).
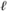What can we say about Np (XA,B)? We begin with a simple heuristic. There are p choices for x in p. For each choice of x, there are either zero, one, or two choices for y, depending on whether x(x - A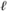)(x + B) is a quadratic nnnresidue, zero, or a quadratic residue in p. Since there are equally many quadratic residues and nonresidues in p, we might guess that those two cases arise equally often. If so, there would on average be one choice of y for each of the p choices of x, which inclines us to make the estimate Np(XA,B) ~ p. Define ap to be the error in this estimate: ap = p - Np(XA,B). It is worth remembering that when X was the scheme attached to x2 + y2 = 1, the behavior of p - Np(X) was very regular; in particular, this quantity took the value 1 at primes congruent to 1 mod 4 and -1 at primes congruent to 3 mod 4. (We note, in particular, that the heuristic estimate Np(X) ~ p is quite good in this case.) Might one hope that ap displays the same kind of regularity?
In fact, the behavior of the ap is very irregular, as a famous theorem of Mazur shows; not only do the ap fail to vary periodically, even their reductions modulo various primes are irregular!
Fact (Mazur). Suppose that 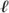is a prime greater than 3, and let b be a positive integer. It is not the case that ap takes the same value (mod 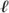) for all primes p congruent to 1 (mod b).5
On the other hand—if I may compress a 200-page paper into a slogan—Wiles proved that, when A, B, C is a solution to (11), the reductions mod 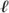of the ap necessarily behaved periodically, contradicting Mazur’s theorem when 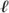> 3. The case 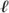= 3 is an old theorem of EULER [VI.19]. This completes the proof of Fermat’s conjecture, and, I hope, bolsters our assertion that the careful study of the values Np (X) is an interesting way to study a variety X!
But the story does not end with Fermat. In general, if f(x) is a cubic polynomial with coefficients in and no repeated roots, the curve E defined by the equation
is called an ELLIPTIC CURVE [III.21] (note well that an elliptic curve is not an ellipse). The study of rational points on elliptic curves (that is, pairs of rational numbers satisfying (12)) has been occupying arithmetic geometers since before our subject existed as such; a decent treatment of the story would fill a book, as indeed it does fill the book of Silverman and Tate (1992). We can define ap(E) to be p - Np(E) as above. First of all, if our heuristic Np(E) ~ p is a good estimate, we might expect that ap(E) is small compared with p; and, in fact, a theorem of Hasse from the 1930s shows that ap (E)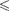 
2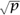 
for all but finitely many p.
It turns out that some elliptic curves have infinitely many rational points, and some only finitely many. One might expect that an elliptic curve with many points over would tend to have more points over finite fields as well, since the coordinates of a rational point can be reduced mod p to yield a point over the finite field p. Conversely, one might imagine that, by knowing the list of numbers ap, one could draw conclusions about the points of E over .
In order to draw such conclusions, one needs a nice way to package the information of the infinite list of integers ap. Such a package is given by the L-FUNCTION [III.47] of the elliptic curve, defined to be the following function of a variable s:
The notation Π′ means that this product is evaluated over all primes apart from a finite set, which is easy to determine from the polynomial f. (As is often the case, we are oversimplifying; what I have written here differs in some irrelevant-to-us respects from what is usually called L(E, s) in the literature.) It is not hard to check that (13) is a convergent product when s is a real number greater than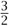 
. Not much deeper is the fact that the right-hand side of (13) is well-defined when s is a complex number whose real part exceeds 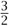. What is much deeper—following from the theorem of Wiles, together with later theorems of Breuil, Conrad, Diamond, and Taylor—is that we can extend L(E, s) to a HOLOMORPHIC FUNCTION [I.3 § 5.6] defined for every complex number s.
A heuristic argument might suggest the following relationship between the values of Np(E) and the value of L(E, 1). If the ap are typically negative (corresponding to the Np(E) typically being greater than p) the terms in the infinite product tend to be smaller than 1; when the ap are positive, the terms in the product tend to be larger than 1. In particular, one might expect the value of L(E, 1) to be closer to 0 when E has many rational points. Of course, this heuristic should be taken with a healthy pinch of salt, given that L(E, 1) is not in fact defined by the infinite product on the right-hand side of (13)! Nonetheless, THE BIRCH-SWINNERTON-DYER CONJECTURE [V.4], which makes precise the heuristic prediction above, is widely believed, and supported by many partial results and numerical experiments. We do not have the space here to state the conjecture in full generality. However, the following conjecture would follow from Birch-Swinnerton-Dyer.
Conjecture. The elliptic curve E has infinitely many points over if and only if L(E, 1) = 0.
Kolyvagin proved one direction of this conjecture in 1988: that E has finitely many rational points if L(E, 1) # 0. (To be precise, he proved a theorem that yields the assertion here once combined with the later theorems of Wiles and others.) It follows from a theorem of Gross and Zagier that E has infinitely many rational points if L(E, s) has a simple zero at s = 1. That more or less sums up our present knowledge about the relationship between L-functions and rational points on elliptic curves. This lack of knowledge has not, however, prevented us from constructing a complex of ever more rarefied conjectures in the same vein, of which the Birch-Swinnerton-Dyer conjecture is only a tiny and relatively down-to-earth sliver.
Before we leave the subject of counting points behind, we will pause and point out one more beautiful result: the theorem of ANDRÉ WEIL [VI.93] bounding the number of points on a curve over a finite field. (Because we have not introduced projective geometry, we will satisfy ourselves with a somewhat less beautiful formulation than the usual one.) Let F(x,y) be an irreducible polynomial in two variables, and let X be the scheme of solutions of F(x,y) = 0. Then the complex points of X define a certain subset of 2, which we call an algebraic curve. Since X is obtained by imposing one polynomial condition on the points of 2, we expect that X has complex dimension 1, which is to say it has real dimension 2. Topologically speaking, X() is, therefore, a surface. It turns out that, for almost all choices of F, the surface X() will have the topology of a “g-holed doughnut” with d points removed, for some nonnegative integers g and d. In this case we say that X is a curve of genus g.
In section 2 we saw that the behavior of schemes over finite fields seemed to “remember” facts arising from our geometric intuition over and : our example there was the fact that circles and lines intersect in at most two points.
The theorem of Weil reveals a similar, though much deeper, phenomenon.
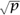Fact. Suppose the scheme X of solutions of F(x,y) is a curve of genus g. Then, for all but finitely many primes p, the number of points of X over p is at most p + 1 + 2g and at least p + 1 - 2g 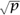- d.
Weil’s theorem illustrates the startlingly close bonds between geometry and arithmetic. The more complicated the topology of X(), the further the number of p-points can vary from the “expected” answer of p. What is more, it turns out that knowing the size of the set X(q) for every finite field q allows us to determine the genus of X. In other words, the finite sets of points X(q) somehow “remember” the topology of the space of complex points X()! In modern language, we say that there is a theory applying to general schemes, called étale cohomology, which mimics the theory of cohomology applying to the topology of varieties over .
Let us return for a moment to our favorite curve, by taking the polynomial F(x,y) = x2 + y2 - 1. In this case, it turns out that X() has g = 0 and d = 2: our previous result that X(p) contains either p + 1 or p - 1 points therefore conforms exactly with the Weil bounds. We also remark that elliptic curves always have genus 1; so the theorem of Hasse alluded to above is a special case of Weil’s theorem as well.
Recall from section 2 that the solutions to x2 + y2 = 1, over , over , or over various finite fields, could be parametrized by the variable m. It was this parametrization that enabled us to determine a simple formula for the size of X(p) in this case. We remarked earlier that most schemes could not be so parametrized; now we can make that statement a bit more precise, at least for algebraic curves.
Fact. If X is a genus-0 curve, then the points of X can be parametrized by a single variable.
The converse of this fact is more or less true as well (though stating it properly requires us to say more than we can here about “singular curves”). In other words, a thoroughly algebraic question—whether the solutions of a Diophantine equation can be parametrized—is hereby given a geometric answer.
As we said above, some elliptic curves (which are curves of genus 1) have finitely many rational points, and others have infinitely many. What is the situation for algebraic curves of other flavors?
We have already encountered a curve of genus 0 with infinitely many points: namely, the curve x2 + y2 = 1. On the other hand, the curve x2 + y2 = 7 also has genus 0, and a simple modification of the argument of the first section shows that this curve has no rational points. It turns out these are the only two possibilities.
Fact. If X is a curve of genus 0, then X() is either empty or infinite
Genus-1 curves are known to fall into a similar dichotomy, thanks to the theorem of Mazur we alluded to earlier.
Fact. If X is a genus-1 curve, then either X has at most sixteen rational points or it has infinitely many rational points.
What about curves of higher genus? In the early 1920s, Mordell made the following conjecture.
Conjecture. If X is a curve of genus greater than 2, then X has finitely many rational points.
This conjecture was proved by Faltings in 1983; in fact, he proved a more general theorem of which this conjecture is a special case. It is worth remarking that the work of Faltings involves a great deal of importation of geometric intuition to the study of the scheme Spec .
When you prove that a set is finite, it is natural to wonder whether you can bound its size. For example, if f (x) is a degree 6 polynomial with no repeated roots, the curve y2 = f (x) turns out to have genus 2; so by Faltings’s theorem there are only finitely many pairs of rational numbers (x,y) satisfying y2 = f (x).
Question. Is there a constant B such that, for all degree 6 polynomials with coefficients in and no repeated roots, the equation y2 = f (x) has at most B solutions?
This question remains open, and I do not think there is a strong consensus about whether the answer will be yes or no. The current world record is held by the curve y2 = 378 371081x2(x2 - 9)2 - 229 833 600(x2 - 1)2, which was constructed by Keller and Kulesz and has 588 rational points.
Interest in the above question comes from its relation to a conjecture of Lang, which involves points on higher-dimensional varieties. Caporaso, Harris, and Mazur showed that Lang’s conjecture implies a positive answer to the question above. This suggests a natural attack on the conjecture: if one can find a way to construct an infinite sequence of degree 6 polynomials f (x) so that the equations y = f(x) have ever more numerous rational solutions, then one has a disproof of Lang’s conjecture! No one has yet been successful at this task. If one could prove that the answer to the question above was affirmative, it would probably bolster our faith in the correctness of Lang’s conjecture, though of course it would bring us no nearer to turning the conjecture into a theorem.
In this article we have seen only a glimpse of the modern theory of arithmetic geometry, and perhaps I have overemphasized mathematicians successes at the expense of the much larger territory of questions, like Lang’s conjecture above, about which we remain wholly ignorant. At this stage in the history of mathematics, we can confidently say that the schemes attached to Diophantine problems have geometry. What remains is to say as much as we can about what this geometry is like, and in this respect, despite the progress described here, our understanding is still quite unsatisfactory when compared with our knowledge of more classical geometric situations.
Dieudonné, J. 1985. History of Algebraic Geometry. Monterey, CA: Wadsworth.
Silverman, J., and J. Tate. 1992. Rational Points on Elliptic Curves. New York: Springer.
1. Exercise: why does our argument not obtain a contradiction from the solution x = y = z = 0?
2. Note that (A), unlike (G), contains no mention of tangency; that is because the notion of tangency is more subtle in the algebraic setting, as we will see in section 4 below.
3. Of course, in real life, there are nouns whose relationship with “yellow” is not so clear-cut, but since our goal is to make this look like mathematics, let us pretend that every object in the world is either definitively yellow or definitively not yellow.
4. In this case, the right attitude to adopt is that L2 is not tangent to V. but that there are certain nontangent lines that intersect the circle at a single point.
5. The theorem proved by Mazur is stated by him in a very different and much more general way: he proves that certain modular curves do not possess any rational points. This implies that a version of the fact above is true, not only for XA,B, but for any equation of the form y2 = f (x), where f is a cubic polynomial without repeated roots. We will leave it to the other able treatments of Fermat to develop that point of view.