 2 that pass through the origin.
2 that pass through the origin.Many of the most important problems in mathematics concern CLASSIFICATION [I.4 §2]. One has a class of mathematical objects and a notion of when two objects should count as equivalent. It may well be that two equivalent objects look superficially very different, so one wishes to describe them in such a way that equivalent objects have the same description and inequivalent objects have different descriptions.
Moduli spaces can be thought of as geometric solutions to geometric classification problems. In this article we shall illustrate some of the key features of moduli spaces, with an emphasis on the moduli spaces of RIEMANN SURFACES [III.79]. In broad terms, a moduli problem consists of three ingredients.
Objects: which geometric objects would we like to describe, or parametrize?
Equivalences: when do we identify two of our objects as being isomorphic, or the “same”?
Families: how do we allow our objects to vary, or modulate?
In this article we will discuss what these ingredients signify, as well as what it means to solve a moduli problem, and we will give some indications as to why this might be a good thing to do.
Moduli spaces arise throughout ALGEBRAIC GEOMETRY [IV.4], differential geometry, and ALGEBRAIC TO POLOGV [IV.6]. (Moduli spaces in topology are often referred to as classifying spaces.) The basic idea is to give a geometric structure to the totality of the objects we are trying to classify. If we can understand this geometric structure, then we obtain powerful insights into the geometry of the objects themselves. Furthermore, moduli spaces are rich geometric objects in their own right. They are “meaningful” spaces, in that any statement about their geometry has a “modular” interpretation, in terms of the original classification problem. As a result, when one investigates them one can often reach much further than one can with other spaces. Moduli spaces such as the moduli Of ELLIPTIC CURVES [III.21] (which we discuss below) play a central role in a variety of areas that have no immediate link to the geometry being classified, in particular in ALGEBRAIC NUMBER THEORY [IV.1] and algebraic topology. Moreover, the study of moduli spaces has benefited tremendously in recent years from interactions with physics (in particular with STRING THEORY [IV.17 §2]). These interactions have led to a variety of new questions and new techniques.
Let us begin with a problem that looks rather simple, but that nevertheless illustrates many of the important ideas of moduli spaces.
Problem. Describe the collection of all lines in the real plane  2 that pass through the origin.
2 that pass through the origin.
To save writing, we are using the word “line” to mean “line that passes through the origin.” This classification problem is easily solved by assigning to each line L an essential parameter, or modulus, a quantity that we can calculate for each line and that will help us tell different lines apart. All we have to do is take standard Cartesian coordinates x,y on the plane and measure the angle θ(L) between the line L and the x-axis, taken in counterclockwise fashion. We find that the possible values of θ are those for which 0 ≤ θ < π, and that for every such θ there is exactly one line L that makes an angle of θ with the x-axis. So as a set, we have a complete solution to our classification problem: the set of lines L, known as the real projective line 
 1, is in one-to-one correspondence with the half-open interval [0, π).
1, is in one-to-one correspondence with the half-open interval [0, π).
However, we are seeking a geometric solution to the classification problem. What does this entail? We have a natural notion of when two lines are near each other, which our solution should capture—in other words, the collection of lines has a natural TOPOLOGY [III.90]. So far, our solution does not reflect the fact that lines L for which the angle θ(L) is close to π are almost horizontal: they are therefore close to the x-axis (for which θ = 0) and to the lines L with θ(L) close to zero. We need to find some way of “wrapping around” the interval [0, π) so that π becomes close to 0.
One way to do this is to take not the half-open interval [0, π) but the closed interval [0, π], and then to “identify” the points 0 and π. (This idea can easily be made formal by defining an appropriate EQUIVALENCE RELATION [I.2 §2.3].) If π and 0 are regarded as the same, then numbers close to π are close to numbers close to 0. This is a way of saying that if you attach the two ends of a line segment together, then, topologically speaking, you obtain a circle.
A more natural way of achieving the same end is suggested by the following geometric construction of 
 1. Consider the unit circle S1 ⊂
1. Consider the unit circle S1 ⊂  2. To each point s ∈ S1, there is an obvious way of assigning a line L(s): take the line that passes through s and the origin. Thus, we have a family of lines parametrized by S1, that is, a map (or function) s
2. To each point s ∈ S1, there is an obvious way of assigning a line L(s): take the line that passes through s and the origin. Thus, we have a family of lines parametrized by S1, that is, a map (or function) s  L(s) that takes points in S1 to lines in our set
L(s) that takes points in S1 to lines in our set 
 1. What is important about this is that we already know what it means for two points in S1 to be close to each other, and the map s
1. What is important about this is that we already know what it means for two points in S1 to be close to each other, and the map s  L(s) is continuous. However, this map is a two-to-one function rather than a bijection, since s and -s always give the same line. To remedy this, we can identify each s in the circle S1 with its antipodal point -s. We then have a one- to-one correspondence between
L(s) is continuous. However, this map is a two-to-one function rather than a bijection, since s and -s always give the same line. To remedy this, we can identify each s in the circle S1 with its antipodal point -s. We then have a one- to-one correspondence between 
 1 and the resulting QUOTIENT SPACE [I.3 §3.3] (which again is topologically a circle), and this correspondence is continuous in both directions.
1 and the resulting QUOTIENT SPACE [I.3 §3.3] (which again is topologically a circle), and this correspondence is continuous in both directions.
The key feature of the space 
 1, considered as the moduli space of lines in the plane, is that it captures the ways in which lines can modulate, or vary continuously in families But when do families of lines arise? A good example is provided by the following construction. Whenever we have a continuous curve C ⊂
1, considered as the moduli space of lines in the plane, is that it captures the ways in which lines can modulate, or vary continuously in families But when do families of lines arise? A good example is provided by the following construction. Whenever we have a continuous curve C ⊂  2 \ 0 in the plane, we can assign to each point c in C the line L(c) that passes through 0 and c. This gives us a family of lines parametrized by C. Moreover, the function that takes c to L(c) is a continuous function from C to
2 \ 0 in the plane, we can assign to each point c in C the line L(c) that passes through 0 and c. This gives us a family of lines parametrized by C. Moreover, the function that takes c to L(c) is a continuous function from C to 
 1, so the parametrization is a continuous one.
1, so the parametrization is a continuous one.
Suppose, for example, that C is a copy of  realized as the set of points (x, 1) at height 1. Then the map from C to
realized as the set of points (x, 1) at height 1. Then the map from C to 
 1 gives an isomorphism between
1 gives an isomorphism between  and the set {L : θ(L) ≠ 0}, which is the subset of
and the set {L : θ(L) ≠ 0}, which is the subset of 
 1 consisting of all lines apart from the x-axis. Put more abstractly, we have an intuitive notion of what it means for a collection of lines through the origin to depend continuously on some parameters, and this notion is captured precisely by the geometry of
1 consisting of all lines apart from the x-axis. Put more abstractly, we have an intuitive notion of what it means for a collection of lines through the origin to depend continuously on some parameters, and this notion is captured precisely by the geometry of 
 1: for instance, if you tell me you have a continuous 37-parameter family of lines in
1: for instance, if you tell me you have a continuous 37-parameter family of lines in  2, this is the same as saying that you have a continuous map from
2, this is the same as saying that you have a continuous map from  37 to
37 to 
 1, which sends a point v ∈
1, which sends a point v ∈  37 to a line L(v) ∈
37 to a line L(v) ∈ 
 1. (More concretely, we could say that the real function v
1. (More concretely, we could say that the real function v  θ(L(v)) on
θ(L(v)) on  37 is continuous away from the locus where θ is close to π. Near this locus we could use instead the function ϕ that measures the angle from the y-axis.)
37 is continuous away from the locus where θ is close to π. Near this locus we could use instead the function ϕ that measures the angle from the y-axis.)
The idea of families of lines leads to various other geometric structures on the space 
 1, and not just its topological structure. For example, we have the notion of a differentiable family of lines in the plane, which is a family of lines for which the angles vary differentiably. (The same ideas apply if we replace “differentiable” by “measurable,” “C∞,” “real analytic,” etc.) To parametrize such a family appropriately, we would like
1, and not just its topological structure. For example, we have the notion of a differentiable family of lines in the plane, which is a family of lines for which the angles vary differentiably. (The same ideas apply if we replace “differentiable” by “measurable,” “C∞,” “real analytic,” etc.) To parametrize such a family appropriately, we would like 
 1 to be a DIFFERENTIABLE MANIFOLD [I.3 §6.9], so that we can calculate derivatives of functions on it. Such a structure on
1 to be a DIFFERENTIABLE MANIFOLD [I.3 §6.9], so that we can calculate derivatives of functions on it. Such a structure on 
 1 can be specified by using the angle functions θ and ϕ defined in the previous section. The function θ gives us a coordinate for lines that are not too close to the x-axis, and ϕ gives us a coordinate for lines that are not too close to the y-axis. We can calculate derivatives of functions on
1 can be specified by using the angle functions θ and ϕ defined in the previous section. The function θ gives us a coordinate for lines that are not too close to the x-axis, and ϕ gives us a coordinate for lines that are not too close to the y-axis. We can calculate derivatives of functions on 
 1 by writing them in terms of these coordinates. One can justify this differentiable structure on
1 by writing them in terms of these coordinates. One can justify this differentiable structure on 
 1 by checking that for any differentiable curve C ⊂
1 by checking that for any differentiable curve C ⊂  2 \ 0 the map c
2 \ 0 the map c  L(c) comes out as differentiable. This means that if L(c) is not close to the x-axis, then the function x
L(c) comes out as differentiable. This means that if L(c) is not close to the x-axis, then the function x  θ(L(x)) is differentiable at x = c, and similarly for ϕ and the y-axis. The functions x
θ(L(x)) is differentiable at x = c, and similarly for ϕ and the y-axis. The functions x  θ(L(x)) and
θ(L(x)) and  ϕ(L(x)) are called pullbacks, because they are the result of converting, or “pulling back,” θ and ϕ from functions defined on
ϕ(L(x)) are called pullbacks, because they are the result of converting, or “pulling back,” θ and ϕ from functions defined on 
 1 to functions defined on C.
1 to functions defined on C.
We now can state the fundamental property of 
 1 as a differentiable space.
1 as a differentiable space.
A differentiable family of lines in  2 parametrized by a differentiable manifold X is the same thing as a function from X to
2 parametrized by a differentiable manifold X is the same thing as a function from X to 
 1, taking a point x to a line L(x), such that the pullbacks x
1, taking a point x to a line L(x), such that the pullbacks x  θ(L(x)) and x
θ(L(x)) and x  ϕ(L(x)) of the functions θ, ϕ are differentiable functions.
ϕ(L(x)) of the functions θ, ϕ are differentiable functions.
We say that 
 1 (with its differentiable structure) is the moduli space of (differentiably varying families of) lines in
1 (with its differentiable structure) is the moduli space of (differentiably varying families of) lines in  2. This means that
2. This means that 
 1 carries the universal differentiable family of lines. From the very definition, we have assigned to each point of
1 carries the universal differentiable family of lines. From the very definition, we have assigned to each point of 
 1 a line in
1 a line in  2, and these lines vary differentiably as we vary the point. The above assertion says that any differentiable family of lines, parametrized by a space X, is described by giving a map f : X →
2, and these lines vary differentiably as we vary the point. The above assertion says that any differentiable family of lines, parametrized by a space X, is described by giving a map f : X → 
 1 and assigning to x ∈ X the line L(f(x)).
1 and assigning to x ∈ X the line L(f(x)).
It is interesting to reformulate the notion of a (continuous or differentiable) family of lines as follows. Let X be a space and let x  L(x) be an assignment of lines to points in X. For each point x ∈ X, we place a copy of
L(x) be an assignment of lines to points in X. For each point x ∈ X, we place a copy of  2 at x; in other words, we consider the Cartesian product X ×
2 at x; in other words, we consider the Cartesian product X ×  2. We may now visualize the line L(x) as living in the copy of
2. We may now visualize the line L(x) as living in the copy of  2 that lies over x. This gives us a continuously varying collection of lines L(x) parametrized by x ∈ X, otherwise known as a line bundle over X. Moreover, this line bundle is embedded in the “trivial” VECTOR BUNDLE [IV.6 §5] X ×
2 that lies over x. This gives us a continuously varying collection of lines L(x) parametrized by x ∈ X, otherwise known as a line bundle over X. Moreover, this line bundle is embedded in the “trivial” VECTOR BUNDLE [IV.6 §5] X ×  2, which is the constant assignment that takes each x to the plane
2, which is the constant assignment that takes each x to the plane  2. In the case when X is
2. In the case when X is 
 1 itself, we have a “tautological” line bundle: to each point s ∈
1 itself, we have a “tautological” line bundle: to each point s ∈ 
 1, which we can think of as a line Ls in
1, which we can think of as a line Ls in  2, it assigns that very same line Ls.
2, it assigns that very same line Ls.
Proposition. For any topological space X there is a natural bijection between the following two sets:
(i) the set of continuous functions f: X → 
 1; and
1; and
(ii) the set of line bundles on X that are contained in the trivial vector bundle X ×  2.
2.
This bijection sends a function f to the corresponding pullback of the tautological line bundle on 
 1. That is, the function f is mapped to the line bundle x
1. That is, the function f is mapped to the line bundle x  Lf(x). (This is a pullback because it converts L from a function defined on
Lf(x). (This is a pullback because it converts L from a function defined on 
 1 to a function defined on X.)
1 to a function defined on X.)
Thus, the space 
 1 carries the universal line bundle that sits in the trivial
1 carries the universal line bundle that sits in the trivial  2 bundle—any time we have a line bundle sitting in the trivial
2 bundle—any time we have a line bundle sitting in the trivial  2 bundle, we can obtain it by pulling back the universal (tautological) example on
2 bundle, we can obtain it by pulling back the universal (tautological) example on 
 1.
1.
Associated with any continuous function f from the circle S1 to itself is an integer known as its degree. Roughly speaking, the degree of f is the number of times f(x) goes around the circle when x goes around once. (If it goes backwards n times, then we say that the degree is -n.) Another way to think of the degree is as the number of times a typical point in S1 is passed by f(x) as x goes around the circle, where we count this as +1 if it is passed in the counterclockwise direction and -1 if it is passed in the clockwise direction.
Earlier, we showed that the circle S1, which we obtained by identifying the endpoints of the closed interval [0, π], could be used to parametrize the moduli space 
 1 of lines. Combining this with the notion of degree, we can draw some interesting conclusions. In particular, we can define the notion of winding numbers. Suppose that we are given a continuous function
1 of lines. Combining this with the notion of degree, we can draw some interesting conclusions. In particular, we can define the notion of winding numbers. Suppose that we are given a continuous function 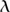 from the circle S1 into the plane
from the circle S1 into the plane  2 and suppose that it avoids 0. The image of this map will be a closed loop C (which may cross itself). This defines for us a map from S1 to itself: first do
2 and suppose that it avoids 0. The image of this map will be a closed loop C (which may cross itself). This defines for us a map from S1 to itself: first do 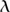 to obtain a point c in C, then work out L(c), which belongs to
to obtain a point c in C, then work out L(c), which belongs to 
 1, and finally use the parametrization of
1, and finally use the parametrization of 
 1 to associate with L(c) a point in S1 again. The degree of the resulting composite map will be twice the number of times that
1 to associate with L(c) a point in S1 again. The degree of the resulting composite map will be twice the number of times that 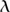 , and hence C, winds around 0, so half this number is defined to be the winding number of
, and hence C, winds around 0, so half this number is defined to be the winding number of 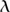 .
.
More generally, given a family of lines in  2 parametrized by some space X, we would like to measure the “manner in which X winds around the circle.” To be precise, given a function ϕ from X to
2 parametrized by some space X, we would like to measure the “manner in which X winds around the circle.” To be precise, given a function ϕ from X to 
 1, which defines the parametrized family of lines, we would like to be able to say, for any map f : S1 → X, what the winding number is of the composition ϕf, which takes a point x in S1 to its image f(x) in X and from there to the corresponding line ϕ(f(x)) in the family. Thus, the map ϕ gives us a way of assigning to each function f : S1 → X an integer, the winding number of ϕf. The way this assignment works does not change if ϕ is continuously deformed: that is, it is a topological invariant of ϕ. What it does depend on is the class that ϕ belongs to in the first COXOMOLOCY CROUP [IV.6 §4] of X, H1(X,
1, which defines the parametrized family of lines, we would like to be able to say, for any map f : S1 → X, what the winding number is of the composition ϕf, which takes a point x in S1 to its image f(x) in X and from there to the corresponding line ϕ(f(x)) in the family. Thus, the map ϕ gives us a way of assigning to each function f : S1 → X an integer, the winding number of ϕf. The way this assignment works does not change if ϕ is continuously deformed: that is, it is a topological invariant of ϕ. What it does depend on is the class that ϕ belongs to in the first COXOMOLOCY CROUP [IV.6 §4] of X, H1(X,  ). Equivalently, to any line bundle on a space X which is contained in the trivial
). Equivalently, to any line bundle on a space X which is contained in the trivial  2-bundle, we have associated a cohomolcgy class, known as the Euler class of the bundle. This is the first example of a CHARACTERISTIC CLASS [IV.6 §5] for Vector bundles. It demonstrates that if we understand the topology of moduli spaces of classes of geometric objects, then we can define topological invariants for families of those objects.
2-bundle, we have associated a cohomolcgy class, known as the Euler class of the bundle. This is the first example of a CHARACTERISTIC CLASS [IV.6 §5] for Vector bundles. It demonstrates that if we understand the topology of moduli spaces of classes of geometric objects, then we can define topological invariants for families of those objects.
We now turn our attention to perhaps the most famous examples of moduli spaces, the moduli spaces of curves, and their first cousins, the Teichmüller spaces. These moduli spaces are the geometric solution to the problem of classification of compact Riemann surfaces, and can be thought of as the “higher theory” of Riemann surfaces. The moduli spaces are “meaningful spaces,” in that each of their points stands for a Riemann surface. As a result, any statement about their geometry tells us something about the geometry of Riemann surfaces.
We turn first to the objects. Recall that a Riemann surface is a topological surface X (connected and oriented) to which a complex structure has been given. Complex structures can be described in many ways, and they enable us to do complex analysis, geometry, and algebra on the surface X. In particular, they enable us to define HOLOMORPHIC [I.3 §5.6] (complex-analytic) and MEROMORPHIC FUNCTIONS [V.31] On Open subsets of X. To be precise, X is a two-dimensional manifold, but the charts are thought of as open subsets of  rather than of
rather than of  , and the maps that glue them together are required to be holomorphic. An equivalent notion is that of a con formal structure on X, which is the structure needed to make it possible to define angles between curves in X. Yet another important equivalent notion is that of algebraic structure on X, making X into a complex-algebraic curve (leading to the persistent confusion in terminology: a Riemann surface is two dimensional, and therefore a surface, from the point of view of topology or the real numbers, but one dimensional, and therefore a curve, from the point of view of complex analysis and algebra). An algebraic structure is what allows us to speak of polynomial, rational, or algebraic functions on X, and is usually specified by realizing X as the set of solutions to polynomial equations in complex PROJECTIVE SPACE [III.72]
, and the maps that glue them together are required to be holomorphic. An equivalent notion is that of a con formal structure on X, which is the structure needed to make it possible to define angles between curves in X. Yet another important equivalent notion is that of algebraic structure on X, making X into a complex-algebraic curve (leading to the persistent confusion in terminology: a Riemann surface is two dimensional, and therefore a surface, from the point of view of topology or the real numbers, but one dimensional, and therefore a curve, from the point of view of complex analysis and algebra). An algebraic structure is what allows us to speak of polynomial, rational, or algebraic functions on X, and is usually specified by realizing X as the set of solutions to polynomial equations in complex PROJECTIVE SPACE [III.72] 
 2 (or
2 (or 
 n).
n).
In order to speak of a classification problem, let alone a moduli space, for Riemann surfaces we must next specify when we regard two Riemann surfaces as equivalent. (We postpone the discussion of the final ingredient, the notion of families of Riemann surfaces, to section 2.2.) To do this, we must give a notion of isomorphism between Riemann surfaces: when should two Riemann surfaces X and Y be “identified,” or thought of as giving two equivalent realizations of the same underlying object of our classification? This issue was hidden in our toy example of classifying lines in the plane: there we simply identified two lines if and only if they were equal as lines in the plane. This naive option is not available to us with the more abstractly defined Riemann surfaces. If we considered Riemann surfaces realized concretely as subsets of some larger space—for example, as solution sets to algebraic equations in complex projective space—we could similarly choose to identify surfaces only if they were equal as subsets. However, this is too fine a classification for most applications: what we care about is the intrinsic geometry of Riemann surfaces, and not incidental features that result from the particular way we choose to realize them.
At the other extreme, we might choose to ignore the extra geometric structure that makes a surface into a Riemann surface. That is, we could identify two Riemann surfaces X and Y if they are topologically equivalent, or homeomorphic (the “coffee mug is a doughnut” perspective). The classification of compact Riemann surfaces up to topological equivalence is captured by a single positive integer, the genus g (“number of holes”) of the surface. Any surface of genus zero is homeomorphic to the Riemann sphere 
 1
1  S2, any surface of genus 1 is homeomorphic to a torus S1 × S1, and so on. Thus, in this case there is no issue of “modulation”—the classification is solved by giving a list of possible values of a single discrete invariant.
S2, any surface of genus 1 is homeomorphic to a torus S1 × S1, and so on. Thus, in this case there is no issue of “modulation”—the classification is solved by giving a list of possible values of a single discrete invariant.
However, if we are interested in Riemann surfaces as Riemann surfaces rather than simply as topological manifolds, then this classification is too crude: it completely ignores the complex structure. We would now like to refine our classification to remedy this defect. To this end, we say that two Riemann surfaces X and Y are (conformelly, or holomorphica1ly) equivalent if there is a topological equivalence between them that preserves the geometry, i.e., a homeomorphism that preserves the angles between curves, or takes holomorphic functions to holomorphic functions, or takes rational functions to rational functions. (These conditions are all equivalent.) Note that we still have at our disposal our discrete invariant—the genus of a surface. However, as we shall see, this invariant is not fine enough to distinguish between all inequivalent Riemann surfaces. In fact, it is possible to have families of inequivalent Riemann surfaces that are parametrized by continuous parameters (but we cannot make proper sense of this idea until we have said precisely what is meant by a family of Riemann surfaces). Thus, the next step is to fix our discrete invariant and to try to classify all the different isomorphism classes of Riemann surfaces with the same genus by assembling them in a natural geometric fashion.
An important step toward this classification is the UNIFORMIZATION THEOREM [V.34]. This states that any simply connected Riemann surface is holomorphically isomorphic to one of the following three: the Riemann sphere 
 1, the complex plane
1, the complex plane  , or the upper half-plane
, or the upper half-plane  (equivalently, the unit disk D). Since the UNIVERSAL COVERING SPACE [III.93] of any Riemann surface is a simply connected Riemann surface, the uniformization theorem provides an approach to classifying arbitrary Riemann surfaces. For instance, any COMPACT [III.9] Riemann surface of genus zero is simply connected, and in fact homeomorphic to the Riemann sphere, so the uniformization theorem already solves our classification problem in genus zero: up to equivalence,
(equivalently, the unit disk D). Since the UNIVERSAL COVERING SPACE [III.93] of any Riemann surface is a simply connected Riemann surface, the uniformization theorem provides an approach to classifying arbitrary Riemann surfaces. For instance, any COMPACT [III.9] Riemann surface of genus zero is simply connected, and in fact homeomorphic to the Riemann sphere, so the uniformization theorem already solves our classification problem in genus zero: up to equivalence, 
 1 is the only Riemann surface of genus zero, and so in this case the topological and conformal classifications agree.
1 is the only Riemann surface of genus zero, and so in this case the topological and conformal classifications agree.
Next, we consider Riemann surfaces whose universal cover is  , which is the same as saying that they are quotients of
, which is the same as saying that they are quotients of  . For example, we can look at a quotient of
. For example, we can look at a quotient of  by
by  , which means that we regard two complex numbers z and w as equivalent if z - w is an integer. This has the effect of “wrapping C around” into a cylinder. Cylinders are not compact, but to get a compact surface we could take a quotient by
, which means that we regard two complex numbers z and w as equivalent if z - w is an integer. This has the effect of “wrapping C around” into a cylinder. Cylinders are not compact, but to get a compact surface we could take a quotient by  2 instead: that is, we could regard z and w as equivalent if their difference is of the form a + bi, where a and b are both integers. Now
2 instead: that is, we could regard z and w as equivalent if their difference is of the form a + bi, where a and b are both integers. Now  is wrapped around in two directions and the result is a torus with a complex (or, equivalently, conformal or algebraic) structure. This is a compact Riemann surface of genus 1. More generally, we can replace
is wrapped around in two directions and the result is a torus with a complex (or, equivalently, conformal or algebraic) structure. This is a compact Riemann surface of genus 1. More generally, we can replace  2 by any lattice L, regarding z and w as equivalent if z - w belongs to L. (A lattice L in
2 by any lattice L, regarding z and w as equivalent if z - w belongs to L. (A lattice L in  is an additive subgroup of
is an additive subgroup of  with two properties. First, it is not contained in any line. Second, it is discrete, which means that there is a constant d > 0 such that the distance between any two points in L is at least d. Lattices are also discussed in THE GENERAL GOALS OF MATHEMATICAL RESEARCH [I.4 §4]. A basis for a lattice L is a pair of complex numbers u and v belonging to L such that every z in L can be written in the form au + bv with a and b integers. Such a basis will not be unique: for example, if L =
with two properties. First, it is not contained in any line. Second, it is discrete, which means that there is a constant d > 0 such that the distance between any two points in L is at least d. Lattices are also discussed in THE GENERAL GOALS OF MATHEMATICAL RESEARCH [I.4 §4]. A basis for a lattice L is a pair of complex numbers u and v belonging to L such that every z in L can be written in the form au + bv with a and b integers. Such a basis will not be unique: for example, if L =  ⊕
⊕ , then the obvious basis is u = 1 and v = 1, but u = 1 and v = 1 + i would do just as well.) If we take a quotient of
, then the obvious basis is u = 1 and v = 1, but u = 1 and v = 1 + i would do just as well.) If we take a quotient of  by a lattice, then we again obtain a torus with complex structure. It turns out that any compact Riemann surface of genus 1 can be produced in this way.
by a lattice, then we again obtain a torus with complex structure. It turns out that any compact Riemann surface of genus 1 can be produced in this way.
From a topological point of view, any two tori are the same, but once we consider the complex structure we start to find that different choices of lattice may lead to different Riemann surfaces. Certain changes to L do not have an effect: for example, if we multiply a lattice L by some nonzero complex number λ, then the quotient surface  /L will not be affected. That is,
/L will not be affected. That is,  /L is naturally isomorphic to
/L is naturally isomorphic to  /λL. Therefore, we need only worry about the difference between lattices when one is not a multiple of the other. Geometrically, this says that one cannot be obtained from the other by a combination of rotation and dilation.
/λL. Therefore, we need only worry about the difference between lattices when one is not a multiple of the other. Geometrically, this says that one cannot be obtained from the other by a combination of rotation and dilation.
Notice that by taking the quotient  /L we obtain not just a “naked” Riemann surface, but one equipped with an “origin,” that is, a distinguished point e ∈ E, which is the image of the origin 0 ∈
/L we obtain not just a “naked” Riemann surface, but one equipped with an “origin,” that is, a distinguished point e ∈ E, which is the image of the origin 0 ∈  . In other words, we obtain an elliptic curve:
. In other words, we obtain an elliptic curve:
Definition. An elliptic curve (over  ) is a Riemann surface E of genus 1, equipped with a marked point e ∈ E. Elliptic curves, up to isomorphism, are in bijection with lattices L ⊂
) is a Riemann surface E of genus 1, equipped with a marked point e ∈ E. Elliptic curves, up to isomorphism, are in bijection with lattices L ⊂  up to rotation.
up to rotation.
Remark. In fact, since L ⊂  is a subgroup of the Abelian group
is a subgroup of the Abelian group  , the elliptic curve E =
, the elliptic curve E =  /L is naturally an Abelian group, with e as its identity element. This is an important motivation for keeping e as part of the data that defines an elliptic curve. A more subtle reason for remembering the location of e when we speak of E is that it helps us to define E more uniquely. This is useful, because any surface E of genus 1 has lots of symmetries, Or AUTOMORPHISMS [I.3 §4.1]: there is always a holomorphic automorphism of E taking any point x to any other given point y. (If we think of E as a group, these are achieved by translations.) Thus, if someone hands us another genus-1 surface E′, there may be no way to identify E with E′, or there may be infinitely many ways: we can always compose a given isomorphism between them with a self-symmetry of E. As we will discuss later, automorphisms haunt almost every moduli problem, and are crucial when we consider the behavior of families It is usually convenient to “rigidify” the situation somewhat, so that the possible isomorphisms between different objects are less “floppy” and more uniquely determined. In the case of elliptic curves, distinguishing the point e achieves this by reducing the symmetry of E. Once we do that, there is usually at most one way to identify two elliptic curves (one way, that is, that takes origin to origin).
/L is naturally an Abelian group, with e as its identity element. This is an important motivation for keeping e as part of the data that defines an elliptic curve. A more subtle reason for remembering the location of e when we speak of E is that it helps us to define E more uniquely. This is useful, because any surface E of genus 1 has lots of symmetries, Or AUTOMORPHISMS [I.3 §4.1]: there is always a holomorphic automorphism of E taking any point x to any other given point y. (If we think of E as a group, these are achieved by translations.) Thus, if someone hands us another genus-1 surface E′, there may be no way to identify E with E′, or there may be infinitely many ways: we can always compose a given isomorphism between them with a self-symmetry of E. As we will discuss later, automorphisms haunt almost every moduli problem, and are crucial when we consider the behavior of families It is usually convenient to “rigidify” the situation somewhat, so that the possible isomorphisms between different objects are less “floppy” and more uniquely determined. In the case of elliptic curves, distinguishing the point e achieves this by reducing the symmetry of E. Once we do that, there is usually at most one way to identify two elliptic curves (one way, that is, that takes origin to origin).
We see that Riemann surfaces of genus 1 (with the choice of a marked point) can be described by concrete “linear algebra data”: a lattice L ⊂  , or rather the equivalence class consisting of all nonzero scalar multiples λL of L. This is the ideal setting to study a classification, or moduli, problem. The next step is to find an explicit parametrization of the collection of all lattices, up to multiplication, and to decide in what sense we have obtained a geometric solution to the classification problem.
, or rather the equivalence class consisting of all nonzero scalar multiples λL of L. This is the ideal setting to study a classification, or moduli, problem. The next step is to find an explicit parametrization of the collection of all lattices, up to multiplication, and to decide in what sense we have obtained a geometric solution to the classification problem.
In order to parametrize the collection of lattices, we follow a procedure used for all moduli problems: first parametrize lattices together with the choice of some additional structure, and then see what happens when we forget this choice. For every lattice L we choose a basis ω1, ω2 ∈ L: that is, we represent L as the set of all integer combinations aω1 + bω2. We do this in an oriented fashion: we require that the fundamental parallelogram spanned by ω1 and ω2 is positively oriented. (That is, the numbers 0, ω1, ω1 + ω2, and ω2 list the vertices of the parallelogram in a counterclockwise order. From the geometric point of view of the elliptic curve E, L is the FUNDAMENTAL GROUP [IV.6 §2] Of E, and the orientation condition says that we generate L by two loops, or “meridians,” A = ωl, B = ω2, which are oriented, in that their oriented intersection number A ∩ B is equal to +1 rather than -1.) Since we are interested in lattices only up to multiplication, we can multiply L by a complex number so as to turn ω1 into 1 and hence ω2 into ω = ω2/ω1. The orientation condition now says that ω is in the upper half-plane  : i.e., its imaginary part is positive, Im ω > 0. Conversely, any complex number ω ∈
: i.e., its imaginary part is positive, Im ω > 0. Conversely, any complex number ω ∈  in the upper half-plane determines a unique oriented lattice L =
in the upper half-plane determines a unique oriented lattice L =  1 ⊕
1 ⊕  ω (that is, the set of all integer combinations a + bω of 1 and ω) and no two of these lattices are related by a rotation.
ω (that is, the set of all integer combinations a + bω of 1 and ω) and no two of these lattices are related by a rotation.
What does this tell us about elliptic curves? We saw earlier that an elliptic curve is defined by a lattice L and an identity e. Now we have seen that if we give L some extra structure, namely an oriented basis, then we can parametrize it by a complex number ω ∈  . This makes precise for us the “additional structure” that we want to place on elliptic curves. We say that a marked elliptic curve is an elliptic curve E, e together with the choice of an oriented basis ω1, ω2 for the associated lattice (fundamental group) L of E. The point is that any lattice has infinitely many different bases, which lead to many automorphisms of E. By “marking” one of these bases, we stop them being automorphisms.
. This makes precise for us the “additional structure” that we want to place on elliptic curves. We say that a marked elliptic curve is an elliptic curve E, e together with the choice of an oriented basis ω1, ω2 for the associated lattice (fundamental group) L of E. The point is that any lattice has infinitely many different bases, which lead to many automorphisms of E. By “marking” one of these bases, we stop them being automorphisms.
With our new definition, we can summarize the earlier discussion by saying that marked elliptic curves are in bijection with points ω ∈  of the upper half-plane. The upper half-plane is, however, much more than just a set of points: it carries a host of geometric structures, in particular a topology and a complex structure. In what sense do these structures reflect geometric properties of marked elliptic curves? In other words, in what sense is the complex manifold
of the upper half-plane. The upper half-plane is, however, much more than just a set of points: it carries a host of geometric structures, in particular a topology and a complex structure. In what sense do these structures reflect geometric properties of marked elliptic curves? In other words, in what sense is the complex manifold  , known in this context as the Teichmütlerspace
, known in this context as the Teichmütlerspace  1,1 of genus-1 Riemann surfaces with one marked point, a geometric solution to the problem of classifying marked elliptic curves?
1,1 of genus-1 Riemann surfaces with one marked point, a geometric solution to the problem of classifying marked elliptic curves?
In order to answer this question, we need the notion of a continuous family of Riemann surfaces, and also the notion of a complex-analytic family. A continuous family of Riemcinn surfaces parametrized by a topological space S, such as the circle S1, for example, is a “continuously varying” assignment of a Riemann surface Xs to every point s of S. In our example of the moduli of lines in the plane, a continuous family of lines was characterized by the property that the angles between the lines and the x-axis or y-axis defined continuous functions of the parameters. Geometrically defined collections of lines, such as those produced by a curve C in the plane, then gave rise to continuous families More abstractly, a continuous family of lines defined a line bundle over the parameter space. A good criterion for a family of Riemann surfaces is likewise that any “reasonably defined” geometric quantity that we can calculate for every Riemann surface should vary continuously in the family. For example, a classical construction of Riemann surfaces of genus g comes from taking 4g-gons and gluing opposite sides together. The resulting Riemann surface is fully determined by the edge-lengths and angles of the polygon. Therefore, a continuous family of Riemann surfaces described in this fashion should be precisely a family such that the edge-lengths and angles give continuous functions of the parameter set.
In more abstract topological terms, if we have a collection {Xs, s ∈ S} of Riemann surfaces depending on points in a space S and we wish to make it into a continuous family, then we should give the union 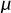 s∈S Xs itself the structure of a topological space X, which should simultaneously extend the topology on each individual Xs. The result is called a Riemann surface bundle. Associated with X is the map that takes each point x to the particular s for which x belongs to Xs. We should demand that this map is continuous, and perhaps more (it could be a fibration, or fiber bundle). This definition has the advantage of great flexibility. For example, if S is a complex manifold, then in just the same way we can speak of a complex-analytic family of Riemann surfaces {Xs, s ∈ S} parametrized by S: now we ask for the union of the Xs to carry not just a topology but a complex structure (i.e., it should form a complex manifold), extending the complex structure on the fibers and mapping holomorphically to the parameter set. The same holds with “complex-analytic” replaced by “algebraic.” These abstract definitions have the property that if our Riemann surfaces are described in a concrete way—cut out by equations, glued from coordinate patches, etc.—then the coefficients of our equations or gluing data will vary as complex-analytic functions in our family precisely when the family is complex analytic (and likewise for continuous or algebraic families)
s∈S Xs itself the structure of a topological space X, which should simultaneously extend the topology on each individual Xs. The result is called a Riemann surface bundle. Associated with X is the map that takes each point x to the particular s for which x belongs to Xs. We should demand that this map is continuous, and perhaps more (it could be a fibration, or fiber bundle). This definition has the advantage of great flexibility. For example, if S is a complex manifold, then in just the same way we can speak of a complex-analytic family of Riemann surfaces {Xs, s ∈ S} parametrized by S: now we ask for the union of the Xs to carry not just a topology but a complex structure (i.e., it should form a complex manifold), extending the complex structure on the fibers and mapping holomorphically to the parameter set. The same holds with “complex-analytic” replaced by “algebraic.” These abstract definitions have the property that if our Riemann surfaces are described in a concrete way—cut out by equations, glued from coordinate patches, etc.—then the coefficients of our equations or gluing data will vary as complex-analytic functions in our family precisely when the family is complex analytic (and likewise for continuous or algebraic families)
As a reality check, note that a (continuous, analytic, or other) family of Riemann surfaces parametrized by a single point s = S is indeed just a single Riemann surface Xs. Just as in this simple case we wish to consider Riemann surfaces only up to equivalence, so there is a notion of equivalence or isomorphism of two analytic families {Xs} and {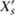 } parametrized by the same space S. We simply regard the families as equivalent if the surfaces Xs and
} parametrized by the same space S. We simply regard the families as equivalent if the surfaces Xs and 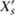 are isomorphic for every s, and if the isomorphism depends analytically on s.
are isomorphic for every s, and if the isomorphism depends analytically on s.
Armed with the notion of family, we can now formulate the characteristic property that the upper half-plane possesses when we think of it as the moduli space of marked elliptic curves. We define a continuous or analytic family of marked elliptic curves to be a family where the underlying genus-1 surfaces vary continuously or analytically, while the choice of basepoint es ∈ Es and the basis of the lattice Ls vary continuously.
The upper half-plane  plays a role for marked elliptic curves that is similar to the role played by
plays a role for marked elliptic curves that is similar to the role played by 
 1 for lines in the plane. The following theorem makes this statement precise.
1 for lines in the plane. The following theorem makes this statement precise.
Theorem. For any topological space S, there is a one-to-one correspondence between continuous maps from S to  and isomorphism classes of continuous families of marked elliptic curves parametrized by S. Similarly, there is a one-to-one correspondence between analytic maps from any complex manifold S to
and isomorphism classes of continuous families of marked elliptic curves parametrized by S. Similarly, there is a one-to-one correspondence between analytic maps from any complex manifold S to  and isomorphism classes of analytic families of marked elliptic curves parametrized by S.
and isomorphism classes of analytic families of marked elliptic curves parametrized by S.
If we apply the theorem in the case where S is a single point, it simply tells us that the points of  are in bijection with the isomorphism classes of marked elliptic curves, as we already knew. However, it contains more information: it says that
are in bijection with the isomorphism classes of marked elliptic curves, as we already knew. However, it contains more information: it says that  , with its topology and complex structure, embodies the structure of marked elliptic curves and the ways in which they can modulate. At the other extreme, we could take S =
, with its topology and complex structure, embodies the structure of marked elliptic curves and the ways in which they can modulate. At the other extreme, we could take S =  itself, mapping S to
itself, mapping S to  by the identity map. This expresses the fact that
by the identity map. This expresses the fact that  itself carries a family of marked elliptic curves, i.e., the collection of Riemann surfaces defined by ω ∈
itself carries a family of marked elliptic curves, i.e., the collection of Riemann surfaces defined by ω ∈  fit together into a complex manifold fibering over
fit together into a complex manifold fibering over  with elliptic curve fibers. This family is called the universal family, since by the theorem any family is “deduced” (or pulled back) from this one universal example.
with elliptic curve fibers. This family is called the universal family, since by the theorem any family is “deduced” (or pulled back) from this one universal example.
We have arrived at a complete and satisfying picture for the classification of elliptic curves when we choose in addition a marking (that is, an oriented basis of the associated lattice L = π1 (E)). What can we say about elliptic curves themselves, without the choice of marking? We somehow need to “forget” the marking, by regarding two points of  as equivalent if they correspond to two different markings of the same elliptic curve.
as equivalent if they correspond to two different markings of the same elliptic curve.
Now, given any two bases of the group (or lattice)  ⊕
⊕  , there is an invertible 2 × 2 matrix with integer entries that takes one basis to the other. If the two bases are oriented, then this matrix will have determinant 1, which means that it is an element
, there is an invertible 2 × 2 matrix with integer entries that takes one basis to the other. If the two bases are oriented, then this matrix will have determinant 1, which means that it is an element

of the group of invertible unimodular matrices over  . Similarly, given any two oriented bases (ω1, ω2) and (
. Similarly, given any two oriented bases (ω1, ω2) and (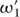 ,
, 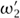 ) of a lattice L, which can be thought of as oriented identifications of L with
) of a lattice L, which can be thought of as oriented identifications of L with  ⊕
⊕  , there is a matrix A ∈ SL2(
, there is a matrix A ∈ SL2( ) such that
) such that 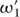 = aω1 + bω2 and
= aω1 + bω2 and 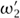 = cω1 + dω2. If we now consider the normalized bases (1, ω) and (1, ω′), where ω = ω1/ω2 and ω′ =
= cω1 + dω2. If we now consider the normalized bases (1, ω) and (1, ω′), where ω = ω1/ω2 and ω′ = 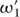 /
/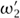 , then we obtain a transformation of the upper half-plane. It is given by the formula
, then we obtain a transformation of the upper half-plane. It is given by the formula
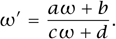
That is, the group SL2( ) is acting on the upper halfplane by linear fractional (or Möbius) transformations with integer coefficients, and two points in the upper half-plane correspond to the same elliptic curve if one can be turned into the other by means of such a transformation. If this is the case, then we should regard the two points as equivalent: that is how we formalize the idea of “forgetting” the marking. Note also that the scalar matrix – Id in SL2(
) is acting on the upper halfplane by linear fractional (or Möbius) transformations with integer coefficients, and two points in the upper half-plane correspond to the same elliptic curve if one can be turned into the other by means of such a transformation. If this is the case, then we should regard the two points as equivalent: that is how we formalize the idea of “forgetting” the marking. Note also that the scalar matrix – Id in SL2( ), which negates both ω1 and ω2, acts trivially on the upper half-plane, so that we in fact get an action of PSL2(
), which negates both ω1 and ω2, acts trivially on the upper half-plane, so that we in fact get an action of PSL2( ) = SL2(
) = SL2( )/{± Id} on
)/{± Id} on  .
.
So we come to the conclusion that elliptic curves (up to isomorphism) are in bijection with orbits of PSL2( ) on the upper half-plane, or equivalently with points of the quotient space
) on the upper half-plane, or equivalently with points of the quotient space  / PSL2(
/ PSL2( ). This quotient space has a natural quotient topology, and in fact can be given a complex-analytic structure, which, it turns out, identifies it with the complex plane
). This quotient space has a natural quotient topology, and in fact can be given a complex-analytic structure, which, it turns out, identifies it with the complex plane  itself. To see this one uses the classical MODULAR FUNCTION [IV.1 8] j(z), a complex-analytic function on
itself. To see this one uses the classical MODULAR FUNCTION [IV.1 8] j(z), a complex-analytic function on  which is invariant under the modular group PSL2(
which is invariant under the modular group PSL2( ) and which therefore defines a natural coordinate
) and which therefore defines a natural coordinate  / PSL2(
/ PSL2( ) →
) →  .
.
It appears that we have solved the moduli problem for elliptic curves: we have a topological, and even complex-analytic, space  1, 1 =
1, 1 =  / PSL2(
/ PSL2( ) whose points are in one-to-one correspondence with isomorphism classes of elliptic curves. This already qualifies
) whose points are in one-to-one correspondence with isomorphism classes of elliptic curves. This already qualifies  1,1 as the coarse moduli space for elliptic curves, which means it is as good a moduli space as we can hope for. However,
1,1 as the coarse moduli space for elliptic curves, which means it is as good a moduli space as we can hope for. However,  1, 1 fails an important test for a moduli space that
1, 1 fails an important test for a moduli space that  1, 1 passed (as we saw in section 2.2): it is not true, even for the circle S = S1, that every continuous family of elliptic curves over S corresponds to a map from S to
1, 1 passed (as we saw in section 2.2): it is not true, even for the circle S = S1, that every continuous family of elliptic curves over S corresponds to a map from S to  1, 1.
1, 1.
The reason for this failure is the problem of automorphisms. These are equivalences from E to itself: that is, complex-analytic maps from E to E that preserve the basepoint e. Equivalently, they are given by complex-analytic self-maps of  that preserve 0 and the lattice L. Such a map must be a rotation: that is, multiplication by some complex number λ of modulus 1. It is easy to check that for most lattices L in the plane, the only rotation that sends L to itself is multiplication by λ = - 1. Note that this is the same - 1 that we quotiented out by to pass from SL2(
that preserve 0 and the lattice L. Such a map must be a rotation: that is, multiplication by some complex number λ of modulus 1. It is easy to check that for most lattices L in the plane, the only rotation that sends L to itself is multiplication by λ = - 1. Note that this is the same - 1 that we quotiented out by to pass from SL2( ) to PSL2(
) to PSL2( ). However, there are two special lattices that have greater symmetry. These are the square lattice L =
). However, there are two special lattices that have greater symmetry. These are the square lattice L =  · 1 ⊕
· 1 ⊕  · i, corresponding to the fourth root of unity i, and the hexagonal lattice L =
· i, corresponding to the fourth root of unity i, and the hexagonal lattice L =  · 1 ⊕
· 1 ⊕  · e2πi/6 corresponding to a sixth root of unity. (Note that the hexagonal lattice is also represented by the point ω = e2πi/3) The square lattice, which corresponds to the elliptic curve formed by gluing the opposite sides of a square, has as its symmetries the group
· e2πi/6 corresponding to a sixth root of unity. (Note that the hexagonal lattice is also represented by the point ω = e2πi/3) The square lattice, which corresponds to the elliptic curve formed by gluing the opposite sides of a square, has as its symmetries the group  /4
/4 of rotational symmetries of the square. The hexagonal lattice, which corresponds to the elliptic curve formed by gluing the opposite sides of a regular hexagon, has as its symmetries the group
of rotational symmetries of the square. The hexagonal lattice, which corresponds to the elliptic curve formed by gluing the opposite sides of a regular hexagon, has as its symmetries the group  /6
/6 of rotational symmetries of a hexagon.
of rotational symmetries of a hexagon.
We see that the number of automorphisms of an elliptic curve jumps discontinuously at the special points ω = i and ω = e2πi/6. This already suggests that something might be wrong with  1, 1 as a moduli space. Note that we avoided this problem with the moduli
1, 1 as a moduli space. Note that we avoided this problem with the moduli  1, 1 of marked elliptic curves, since there are no auto-morphisms of an elliptic curve that also preserve the marking. Another place we might have observed this problem with
1, 1 of marked elliptic curves, since there are no auto-morphisms of an elliptic curve that also preserve the marking. Another place we might have observed this problem with  1, 1 is when we passed to the quotient
1, 1 is when we passed to the quotient  / PSL2(
/ PSL2( ). We avoided the automorphism λ = - 1 by quotienting by PSL2(
). We avoided the automorphism λ = - 1 by quotienting by PSL2( ) rather than SL2(
) rather than SL2( ). However, the two special points i and e2πi/6 are preserved by integer Möbius transformations of
). However, the two special points i and e2πi/6 are preserved by integer Möbius transformations of  other than the identity, and they are the only points with that property. This means that the quotient
other than the identity, and they are the only points with that property. This means that the quotient  / PSL2(
/ PSL2( ) naturally comes with conical singularities at the points corresponding to these two orbits: one looks like a cone with angle π, and the other like a cone with angle
) naturally comes with conical singularities at the points corresponding to these two orbits: one looks like a cone with angle π, and the other like a cone with angle 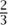 π. (To see why this is plausible, imagine the following simpler instance of the same phenomenon. if for every complex number z you identify z with - z, then the result is to wrap the complex plane around into a cone with a singularity at 0. The reason 0 is singled out is that it is preserved by the transformation z
π. (To see why this is plausible, imagine the following simpler instance of the same phenomenon. if for every complex number z you identify z with - z, then the result is to wrap the complex plane around into a cone with a singularity at 0. The reason 0 is singled out is that it is preserved by the transformation z  - z. Here the angle would be π because the identification of points is two-to-one away from the singularity and π is half of 2π.) It is possible to massage these singularities away using the j-function, but they are indicating a basic difficulty.
- z. Here the angle would be π because the identification of points is two-to-one away from the singularity and π is half of 2π.) It is possible to massage these singularities away using the j-function, but they are indicating a basic difficulty.
So why do automorphisms form an obstacle to the existence of “good” moduli spaces? We can demonstrate the difficulty by considering an interesting continuous family of marked elliptic curves paremetrized by the circle S = S1. Let E(i) be the “square” elliptic curve that we considered earlier, based on the lattice of integer combinations of 1 and i. Next, for every t between 0 and 1, let Et be a copy of E(i). Thus, we have taken the constant, or “trivial,” family of elliptic curves over the closed unit interval [0, 1], where every curve in the family is E(i). Now we identify the elliptic curves at the two ends of this family, not in the obvious way, but by using the automorphism given by a 90° rotation, or multiplication by i. This means that we are looking at the family of elliptic curves over the circle where each member of the family is a copy of the elliptic curve E(i), but these copies twist by 90° as we go around the circle.
It is easy to see that there is no way to capture this family of elliptic curves by means of a map from S1 to the space  1, 1. Since all of the members of the family are isomorphic, each point of the circle should map to the same point in
1, 1. Since all of the members of the family are isomorphic, each point of the circle should map to the same point in  1,1 (the equivalence class of i in
1,1 (the equivalence class of i in  ). But the constant map S1 → {i} ∈
). But the constant map S1 → {i} ∈  1, 1 classifies the trivial family S1 × Ei of elliptic curves over S1, that is, the family where every curve is equal to E(i) but the curves do not twist as we go around! Thus, there are more families of elliptic curves than there are maps to
1, 1 classifies the trivial family S1 × Ei of elliptic curves over S1, that is, the family where every curve is equal to E(i) but the curves do not twist as we go around! Thus, there are more families of elliptic curves than there are maps to  1,1; the quotient space
1,1; the quotient space  / PSL2(
/ PSL2( ) cannot handle the complications caused by automorphisms. A variant of this construction applies to complex-analytic families with S1 replaced by
) cannot handle the complications caused by automorphisms. A variant of this construction applies to complex-analytic families with S1 replaced by  ×. This is a very general phenomenon in moduli problems: whenever objects have nontrivial automorphisms, we can imitate the construction above to get nontrivial families over an interesting parameter set, all of whose members are the same. As a result, they cannot be classified by a map to the set of all isomorphism classes.
×. This is a very general phenomenon in moduli problems: whenever objects have nontrivial automorphisms, we can imitate the construction above to get nontrivial families over an interesting parameter set, all of whose members are the same. As a result, they cannot be classified by a map to the set of all isomorphism classes.
What do we do about this problem? One approach is to resign ourselves to having coarse moduli spaces, which have the right points and right geometry but do not quite classify arbitrary families Another approach is the one that leads to  1, 1: we can fix markings of one kind or another, which “kill all automorphisms. In other words, we choose enough extra structure on our objects so that there do not remain any (nontrivial) automorphisms that preserve all this decoration. In fact, one can be far more economical than picking a basis of the lattice L and obtaining the infinite covering
1, 1: we can fix markings of one kind or another, which “kill all automorphisms. In other words, we choose enough extra structure on our objects so that there do not remain any (nontrivial) automorphisms that preserve all this decoration. In fact, one can be far more economical than picking a basis of the lattice L and obtaining the infinite covering  1,1 of
1,1 of  1, 1: one can fix a basis of L only up to some congruence (for example, of L/2L). Finally, we can simply learn to come to terms with the automorphisms, keeping them as part of the data, resulting in “spaces” where points have internal symmetries. This is the notion of an ORBIFOLD [IV.4 § 7], or STACK [IV.4 § 7], which is flexible enough to deal with essentially all moduli problems.
1, 1: one can fix a basis of L only up to some congruence (for example, of L/2L). Finally, we can simply learn to come to terms with the automorphisms, keeping them as part of the data, resulting in “spaces” where points have internal symmetries. This is the notion of an ORBIFOLD [IV.4 § 7], or STACK [IV.4 § 7], which is flexible enough to deal with essentially all moduli problems.
We would now like to generalize as much as possible of the picture of elliptic curves and their moduli to higher-genus Riemann surfaces. For each g we would like to define a space  g, called the moduli space of curves of genus g, that classifies compact Riemann surfaces of genus g and tells us how they modulate. Thus, the points of
g, called the moduli space of curves of genus g, that classifies compact Riemann surfaces of genus g and tells us how they modulate. Thus, the points of  g should correspond to our objects, compact Riemann surfaces of genus g, or, to be more accurate, equivalence classes of such surfaces, where two surfaces are considered to be equivalent if there is a complex-analytic isomorphism between them. In addition, we would like
g should correspond to our objects, compact Riemann surfaces of genus g, or, to be more accurate, equivalence classes of such surfaces, where two surfaces are considered to be equivalent if there is a complex-analytic isomorphism between them. In addition, we would like  g to do the best it can to embody the structure of continuous families of genus-g surfaces. Likewise, there are spaces
g to do the best it can to embody the structure of continuous families of genus-g surfaces. Likewise, there are spaces  g, n parnmetrizing “n-punctured” Riemann surfaces of genus g. This means we consider not “bare” Riemann surfaces, but Riemann surfaces together with a “decoration” or “marking” by n distinct labeled points (punctures). Two of these are considered to be equivalent if there is a complex-analytic isomorphism between them that takes punctures to punctures and preserves labels. Since there are Riemann surfaces with automorphisms, we do not expect
g, n parnmetrizing “n-punctured” Riemann surfaces of genus g. This means we consider not “bare” Riemann surfaces, but Riemann surfaces together with a “decoration” or “marking” by n distinct labeled points (punctures). Two of these are considered to be equivalent if there is a complex-analytic isomorphism between them that takes punctures to punctures and preserves labels. Since there are Riemann surfaces with automorphisms, we do not expect  g to be able to classify all families of Riemann surfaces: that is, we will expect examples similar to the twisted square-lattice construction discussed earlier. However, if we consider Riemann surfaces with enough extra markings, then we will be able to obtain a moduli space in the strongest sense. One way to choose such markings is to consider
g to be able to classify all families of Riemann surfaces: that is, we will expect examples similar to the twisted square-lattice construction discussed earlier. However, if we consider Riemann surfaces with enough extra markings, then we will be able to obtain a moduli space in the strongest sense. One way to choose such markings is to consider  g, n with n large enough (for fixed g). Another approach will be to mark generators of the fundamental group, leading to the Teichmtiller spaces
g, n with n large enough (for fixed g). Another approach will be to mark generators of the fundamental group, leading to the Teichmtiller spaces  g and
g and  g, n We now outline this process.
g, n We now outline this process.
To construct the space  g, we return to the uniformization theorem. Any compact surface X of genus g > 1 has as its universal cover the upper half-plane
g, we return to the uniformization theorem. Any compact surface X of genus g > 1 has as its universal cover the upper half-plane  , so it is represented as a quotient X =
, so it is represented as a quotient X =  /Γ, where Γ is a representation of the fundamental group of X as a subgroup of conformal self-maps of
/Γ, where Γ is a representation of the fundamental group of X as a subgroup of conformal self-maps of  . The group of all conformal automorphisms of
. The group of all conformal automorphisms of  is PSL2(
is PSL2( ), the group of linear fractional transformations with real coefficients. The fundamental groups of all compact genus-g Riemann surfaces are isomorphic to a fixed abstract group Γg, with 2g generators Ai, Bi(i = 1, . . . ,g) and one relation: that the product of all commutators AiBi
), the group of linear fractional transformations with real coefficients. The fundamental groups of all compact genus-g Riemann surfaces are isomorphic to a fixed abstract group Γg, with 2g generators Ai, Bi(i = 1, . . . ,g) and one relation: that the product of all commutators AiBi
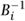 is the identity. A subgroup Γ ⊂ PSL2(
is the identity. A subgroup Γ ⊂ PSL2( ) that acts on
) that acts on  in such a way that the quotient
in such a way that the quotient  /Γ is a Riemann surface (technically, the action should have no fixed points and should be properly discontinuous) is known as a FUCHSIAN GROUP [III.28]. Thus, the analogue of the representation of elliptic curves by lattices L
/Γ is a Riemann surface (technically, the action should have no fixed points and should be properly discontinuous) is known as a FUCHSIAN GROUP [III.28]. Thus, the analogue of the representation of elliptic curves by lattices L 
 ⊕
⊕  in the plane is the representation of higher-genus Riemann surfaces as
in the plane is the representation of higher-genus Riemann surfaces as  /Γ, where Γ is a Fuchsian group.
/Γ, where Γ is a Fuchsian group.
The Teichmtiller space  g of genus-g Riemann surfaces is the space that solves the moduli problem for genus-g surfaces when they come with a marking of their fundamental group. This means that our objects are genus-g surfaces X plus a set of generators Ai, Bi of π1(X), which give an isomorphism between π1(X) and Γg, up to conjugation.1 Our equivalences are complex-analytic maps that preserve the markings. Finally, our continuous (respectively, complex-analytic) families are continuous (complex-analytic) families of Riemann surfaces with continuously varying markings of the fundamental group. In other words, we are asserting the existence of a topological space/complex manifold
g of genus-g Riemann surfaces is the space that solves the moduli problem for genus-g surfaces when they come with a marking of their fundamental group. This means that our objects are genus-g surfaces X plus a set of generators Ai, Bi of π1(X), which give an isomorphism between π1(X) and Γg, up to conjugation.1 Our equivalences are complex-analytic maps that preserve the markings. Finally, our continuous (respectively, complex-analytic) families are continuous (complex-analytic) families of Riemann surfaces with continuously varying markings of the fundamental group. In other words, we are asserting the existence of a topological space/complex manifold  g with a complex-analytic family of marked Riemann surfaces over it, and the following strong property.
g with a complex-analytic family of marked Riemann surfaces over it, and the following strong property.
The characteristic property of  g. For any topological space (respectively, complex manifold) S, there is a bijection between continuous maps (respectively, holomorphic maps) S → Tg and isomorphism classes of continuous (respectively, complex-analytic) families of marked genus-g surfaces parametrized by S.
g. For any topological space (respectively, complex manifold) S, there is a bijection between continuous maps (respectively, holomorphic maps) S → Tg and isomorphism classes of continuous (respectively, complex-analytic) families of marked genus-g surfaces parametrized by S.
It is interesting to note that, while we have yet to see why such a space exists, it follows from general, nongeometric principles—CATEGORY THEORY [III.8] or “abstract nonsense”—that it is completely and uniquely determined, both as a topological space and as a complex manifold, by this characteristic property. In a very abstract way, every topological space M can be uniquely reconstructed from its set of points, the set of paths between these points, the set of surfaces spanning these paths, and so on. To put it differently, we can think of M as a “machine” that assigns to any topological space S the set of continuous maps from S to M. This machine is known as the “functor of points of M.” Similarly, a complex manifold M provides a machine that assigns to any other complex manifold S the set of complex-analytic maps from S to M. A curious discovery of category theory (the Yoneda lemma) is that for very general reasons (having nothing to do with geometry), these machines (or functors) uniquely determine M as a space, or a complex manifold.
Any moduli problem in the sense we have described (giving objects, equivalences, and families) also gives such a machine, where to S we assign the set of all families over S, up to isomorphism. So just by setting up the moduli problem we have already uniquely determined the topology and complex structure on Teichmtiller space. The interesting part then is to know whether or not there actually exists a space giving rise to the same machine we have constructed, whether we can construct it explicitly, and whether we can use its geometry to learn interesting facts about Riemann surfaces.
Coming back to earth, we discover that we have a fairly concrete model of Teichmtiller space at our disposal. Once we have fixed the marking π1(X)  Γg, we are simply looking at all ways to represent Γg as a Fuchsian subgroup of PSL2(
Γg, we are simply looking at all ways to represent Γg as a Fuchsian subgroup of PSL2( ). Ignoring the Fuchsian condition for a moment, this means finding 2g real matrices (up to ± Id) Ai, Bi ∈ PSL2(
). Ignoring the Fuchsian condition for a moment, this means finding 2g real matrices (up to ± Id) Ai, Bi ∈ PSL2( ) satisfying the commutator relation of Γg. This gives an explicit set of (algebraic!) equations for the entries of the 2g matrices, which determine the space of all representations Γg → PSL2(
) satisfying the commutator relation of Γg. This gives an explicit set of (algebraic!) equations for the entries of the 2g matrices, which determine the space of all representations Γg → PSL2( ). We must now quotient out by the action of PSL2(
). We must now quotient out by the action of PSL2( ) that simultaneously conjugates all 2g matrices to obtain the representation variety Rep(Γg, PSL2(
) that simultaneously conjugates all 2g matrices to obtain the representation variety Rep(Γg, PSL2( )). This is analogous to considering lattices in
)). This is analogous to considering lattices in  up to rotation, and is motivated by the fact that the quotients of
up to rotation, and is motivated by the fact that the quotients of  by two conjugate subgroups of PSL2(
by two conjugate subgroups of PSL2( ) will be isomorphic.
) will be isomorphic.
Once we have described the space of all representations of Γg into PSL2( ), we can then single out Teichmtiller space as the subset of the representation variety that consists of Fuchsian representations of Γg into PSL2(
), we can then single out Teichmtiller space as the subset of the representation variety that consists of Fuchsian representations of Γg into PSL2( ). Luckily this subset is open in the representation variety, which gives a nice realization of
). Luckily this subset is open in the representation variety, which gives a nice realization of  g as a topological space—in fact,
g as a topological space—in fact,  g is homeomorphic to
g is homeomorphic to  6g-6 (This can be seen very explicitly in terms of the Fenchel-Nielsen coordinates, which parametrize a surface in
6g-6 (This can be seen very explicitly in terms of the Fenchel-Nielsen coordinates, which parametrize a surface in  g via a cut-and-paste procedure involving 3g - 3 lengths and 3g - 3 angles.) We may now try to “forget” the marking π1(X) ≅ Γg, to obtain the moduli space
g via a cut-and-paste procedure involving 3g - 3 lengths and 3g - 3 angles.) We may now try to “forget” the marking π1(X) ≅ Γg, to obtain the moduli space  g of unmarked Riemann surfaces. In other words, we would like to take
g of unmarked Riemann surfaces. In other words, we would like to take  g and identify any two points that represent the same underlying Riemann surface with different markings. This identification is achieved by the action of a group, the genus-g mapping class group MCGg or Teichmütler modular group, on
g and identify any two points that represent the same underlying Riemann surface with different markings. This identification is achieved by the action of a group, the genus-g mapping class group MCGg or Teichmütler modular group, on  g, which generalizes the modular group PSL2(
g, which generalizes the modular group PSL2( ) that acts on
) that acts on  =
=  1,1. (The mapping class group is defined as the group of all self-diffeomnrphisms of a genus-g surface—remember that all such surfaces are topologically the same—modulo those diffeomorphisms that act trivially on the fundamental group.) As in the case of elliptic curves, Riemann surfaces with automorphisms correspond to points in
1,1. (The mapping class group is defined as the group of all self-diffeomnrphisms of a genus-g surface—remember that all such surfaces are topologically the same—modulo those diffeomorphisms that act trivially on the fundamental group.) As in the case of elliptic curves, Riemann surfaces with automorphisms correspond to points in  g fixed by some subgroup of MCGg, and give rise to singular points in the quotient
g fixed by some subgroup of MCGg, and give rise to singular points in the quotient  g =
g =  g/ MCGg.
g/ MCGg.
Representation varieties, or moduli spaces of representations, are an important and concrete class of moduli spaces that arise throughout geometry, topology, and number theory. Given any (discrete) group Γ, we ask (for example) for a space that parametrizes homomorphisms of Γ into the group of n × n matrices. The notion of equivalence is given by conjugation by GLn, and that of families by continuous (or analytic, or algebraic, etc.) families of matrices. This problem is interesting even when the group Γ is  . Then we are simply considering invertible n × n matrices (the image of 1 ∈
. Then we are simply considering invertible n × n matrices (the image of 1 ∈  ) up to conjugxcy. It turns out that there is no moduli space for this problem, even in the coarse sense, unless we consider only “nice enough” matrices: for example, matrices that consist of only a single Jordan block. This is a good example of a ubiquitous phenomenon in moduli problems: one is often forced to throw out some “bad” (unstable) objects in order to have any chance of obtaining a moduli space. (See the paper by Mumford and Suominen (1972) for a detailed discussion.)
) up to conjugxcy. It turns out that there is no moduli space for this problem, even in the coarse sense, unless we consider only “nice enough” matrices: for example, matrices that consist of only a single Jordan block. This is a good example of a ubiquitous phenomenon in moduli problems: one is often forced to throw out some “bad” (unstable) objects in order to have any chance of obtaining a moduli space. (See the paper by Mumford and Suominen (1972) for a detailed discussion.)
The upper half-plane  =
=  1,1, together with the action of PSL2(
1,1, together with the action of PSL2( ), gives an appealingly complete picture of the moduli problem for elliptic curves and its geometry. The same cannot be said, unfortunately, for the picture of
), gives an appealingly complete picture of the moduli problem for elliptic curves and its geometry. The same cannot be said, unfortunately, for the picture of  g as an open subset of the representation variety. In particular, the representation variety does not even carry a natural complex structure, so we cannot see from this description the geometry of
g as an open subset of the representation variety. In particular, the representation variety does not even carry a natural complex structure, so we cannot see from this description the geometry of  g as a complex manifold. This failure reflects some of the ways in which the study of moduli spaces is more complicated for genus greater than 1. In particular, the moduli spaces of higher-genus surfaces are not described purely by linear algebra plus data about orientation, as is the case in genus 1.
g as a complex manifold. This failure reflects some of the ways in which the study of moduli spaces is more complicated for genus greater than 1. In particular, the moduli spaces of higher-genus surfaces are not described purely by linear algebra plus data about orientation, as is the case in genus 1.
Part of the blame for this complexity lies with the fact that the fundamental group Γg  π1(X) (g > 1) is no longer Abelian, and in particular it is no longer equal to the first homology group H1(X,
π1(X) (g > 1) is no longer Abelian, and in particular it is no longer equal to the first homology group H1(X,  ). A related problem is that X is no longer a group. A beautiful solution to this problem is given by the construction of the Jacobian Jac(X), which shares with elliptic curves the properties of being a torus (homeomurphic to (S1)2g), an Abelian group, and a complex (in fact complex-algebraic) manifold. (The Jacobian of an elliptic curve is the elliptic curve itself.) The Jacobian captures the “Abelian” or “linear” aspects of the geometry of X. There is a moduli space
). A related problem is that X is no longer a group. A beautiful solution to this problem is given by the construction of the Jacobian Jac(X), which shares with elliptic curves the properties of being a torus (homeomurphic to (S1)2g), an Abelian group, and a complex (in fact complex-algebraic) manifold. (The Jacobian of an elliptic curve is the elliptic curve itself.) The Jacobian captures the “Abelian” or “linear” aspects of the geometry of X. There is a moduli space  g for such complex-algebraic tori (known as Abelian varieties), which does share all of the nice properties and linear algebraic description of the moduli of elliptic curves
g for such complex-algebraic tori (known as Abelian varieties), which does share all of the nice properties and linear algebraic description of the moduli of elliptic curves  1,1 =
1,1 =  1. The good news—the Torelli theorem—is that by assigning to each Riemann surface X its Jacobian we embed
1. The good news—the Torelli theorem—is that by assigning to each Riemann surface X its Jacobian we embed  g as a closed, complex-analytic subset of
g as a closed, complex-analytic subset of  g. The interesting news—the Schottky problem—is that the image is quite complicated to characterize intrinsically. In fact, solutions to this problem have come from as far afield as the study of nonlinear partial differential equations!
g. The interesting news—the Schottky problem—is that the image is quite complicated to characterize intrinsically. In fact, solutions to this problem have come from as far afield as the study of nonlinear partial differential equations!
In this section we give hints at some interesting questions about, and applications of, moduli spaces.
Deformations and degenerations. Two of the main topics in moduli spaces ask which objects are very near to a given one, and what lies very far away. Deformation theory is the calculus of moduli spaces: it describes their infinitesimal structure. In other words, given an object, deformation theory is concerned with describing all its small perturbations (see Mazur (2004) for a beautiful discussion of this). At the other extreme, we can ask what happens when our objects degenerate? Most moduli spaces, for example the moduli of curves, are not compact, so there are families “going off to infinity.” It is important to find “meaningful” compactifications of moduli spaces, which classify the possible degenerations of our objects. Another advantage of compactifying moduli spaces is that we can then calculate integrals over the completed space. This is crucial for the next item.
Invariants from moduli spaces. An important application of moduli spaces in geometry and topology is inspired by quantum field theory, where a particle, rather than following the “best” classical path between two points, follows all paths with varying probabilities (see MIRROR SYMMETRY [IV.16 §2.2.4]). Classically, one calculates many topological invariants by picking a geometric structure (such as a metric) on a space, calculating some quantity using this structure, and finally proving that the result of the calculation did not depend on the structure we chose. The new alternative is to look at all such geometric structures, and integrate some quantity over the space of all choices. The result, if we can show convergence, will manifestly not depend on any choices. String theory has given rise to many important applications of this idea, in particular by giving a rich structure to the collection of integrals obtained in this way. Donaldson and Seiberg-Witten theories use this philosophy to give topological invariants of four-manifolds. Gromov-Witten theory applies it to the topology Of SYMPLECTIC MANIFOLDS [III.88], and to counting problems in algebraic geometry, such as, How many rational plane curves of degree 5 pass through fourteen points in general position? (Answer: 87304.)
Modular forms. One of the most profound ideas in mathematics, the Langlands program, relates number theory to function theory (harmonic analysis) on very special moduli spaces, generalizing the moduli space of elliptic curves. These moduli spaces (Shimura varieties) are expressible as quotients of symmetric spaces (such as  ) by arithmetic groups (such as PSL2(
) by arithmetic groups (such as PSL2( )). MODULAR FORMS [III.59] and automorphic forms are special functions on these moduli spaces, described by their interaction with the large symmetry groups of the spaces. This is an extremely exciting and active area of mathematics, which counts among its recent triumphs the proof of FERMAT’S LAST THEOREM [V.10] and the Shimura-Taniyama-Weil conjecture (Wiles, Taylor- Wiles, Breuil-Conrad-Diamond-Taylor).
)). MODULAR FORMS [III.59] and automorphic forms are special functions on these moduli spaces, described by their interaction with the large symmetry groups of the spaces. This is an extremely exciting and active area of mathematics, which counts among its recent triumphs the proof of FERMAT’S LAST THEOREM [V.10] and the Shimura-Taniyama-Weil conjecture (Wiles, Taylor- Wiles, Breuil-Conrad-Diamond-Taylor).
For historical accounts and bibliographies on moduli spaces, the following articles are highly recommended.
A beautiful and accessible overview of moduli spaces, with an emphasis on the notion of deformations, is given by Mazur (2004). The articles by Hain (2000) and Looijenga (2000) give excellent introductions to the study of the moduli spaces of curves, perhaps the oldest and most important of all moduli problems. The article by Mumford and Suominen (1972) introduces the key ideas underlying the study of moduli spaces in algebraic geometry.
Hain, R. 2000. Moduli of Riemann surfaces, transcendental aspects. In School on Algebraic Geometry, Trieste, 1999, pp. 293–353. ICTP Lecture Notes Series, no. 1. Trieste: The Abdus Salam International Centre for Theoretical Physics.
Looijenga, E. 2000. A minicourse on moduli of curves. In School on Algebraic Geometry, Trieste, 1999, pp. 267–91. ICTP Lecture Notes Series, no. 1. Trieste: The Abdus Salam International Centre for Theoretical Physics.
Mazur, B. 2004. Perturbations, deformations and variations (and “near-misses”) in geometry. Physics and number theory. Bulletin of the American Mathematical Society 41(3):307–36.
Mumford, D., and K. Suominen. 1972. Introduction to the theory of moduli. In Algebraic Geometry, Oslo, 1970: Proceedings of the Fifth Nordic Summer School in Mathematics, edited by F. Oort, pp. 171–222. Groningen: Wolters-Noordhoff.
1. Note that while the fundamental group of X depends on the choice of a basepoint, π1(X, x) and π1(X, y) may be identified by choosing a path from x to y, and the different choices are related by conjugation by a loop. Thus, if we are willing to identify sets of generators Ai, Bi when they differ only by a conjugation, then we can ignore the choice of a basepoint.