IV.23 Logic and Model Theory
David Marker
1 Languages and Theories
Mathematical logic is the study of formal languages that are used to describe mathematical structures and what these can tell us about the structures themselves. We can learn a lot about a formal language by investigating which of its sentences are true for the structure it describes, and we can learn a lot about the structure by investigating the subsets of it that can be defined using the language. In this article, we shall see several examples of languages and the structures that they are used to describe. We shall also see instances of the remarkable phenomenon that theorems in logic can sometimes be used to prove “purely mathematical” results that seem to have nothing to do with logic. This introductory section briefly introduces some of the basic ideas that will be needed to understand the later sections.
All the formal languages that we consider will be extensions of a basic logical language that we shall denote by L0. The statements, or formulas, of this language are made up of the following components: variables, which are denoted by letters of the alphabet such as x or y, or letters with subscripts such as ν1, ν2, . . . ; the parentheses “(” and “)”; the equality symbol “=” the logical connectives ∧, ∨, ¬, →, ↔ which we read as “and,” “or” “not,” “implies,” and “if and only if”; and the quantifiers ∃ and ∀, which we read as “there exists” and “for all.” (If these symbols are unfamiliar to you, then you should read THE LANGUAGE AND GRAMMAR OF MATHEMATICS [I.2] before attempting to read this article.) Here are a couple of formulas of L0:
(i) ∀x ∀y ∃z(z ≠ x ∧ z ≠ y);
(ii) ∀x (x = y ∨ x = z).
The first of these says that if any object exists at all then there are at least three objects, and the second says that y and z are the only objects. There is an important difference between the two formulas: the variables x, y, and z that occur in the first formula are all bound variables, which means that they are all attached to quantifiers, whereas in the second formula, only the variable x is bound, while the variables y and z are free. This means that the first formula expresses a statement about some mathematical structure, while the second is a statement about not just a structure but also the particular elements y and z.
There are various rules that allow one to build larger formulas out of smaller ones. We will not give them all, but for example if  and ψ are formulas, then ¬
and ψ are formulas, then ¬ ,
,  ∨ ψ,
∨ ψ,  ∧ ψ,
∧ ψ,  → ψ, and
→ ψ, and  ↔ ψ are all formulas. In general, if
↔ ψ are all formulas. In general, if  is built out of smaller formulas
is built out of smaller formulas  1, . . . ,
1, . . . ,  n using logical connectives (and parentheses), then we call
n using logical connectives (and parentheses), then we call  a Boolean combination of
a Boolean combination of  1, . . . ,
1, . . . ,  n. Another important way to modify a formula is quantification: if
n. Another important way to modify a formula is quantification: if  (x) is a formula involving a free variable x, then ∀x
(x) is a formula involving a free variable x, then ∀x (x) and ∃x
(x) and ∃x (x) are both formulas.
(x) are both formulas.
The formulas just discussed are “purely logical,” which makes them not very useful for describing interesting mathematical structures. Suppose, for example, that we wanted to study real solutions to algebraic and exponential equations over the FIELD [I.3 §2.2] of real numbers. We can think of this as studying the “mathematical structure”
ℝexp = ( ℝ, +, ·, exp, <, 0, 1),
where the right-hand side is a septuple that consists of the set ℝ of real numbers, the binary operations of addition and multiplication, the EXPONENTIAL FUNCTION [III.25], the “less than” relation, and the real numbers 0 and 1.
The various components of this structure are of course related to each other in many ways, but we cannot express these relationships unless we are prepared to extend the basic language L0. For example, if we wanted to write, in a formal way, the statement that the exponential function turns addition into multiplication, then the obvious thing to write down would be
(i) ∀x∀y exp(x) · exp(y) = exp(x + y).
Here we have two quantifiers, two bound variables x and y, and the equals sign, but the rest of the formula involves extraneous elements such as “+”, “·”, and “exp”. Thus, to discuss the structure ℝexp, we extend the language L0 to a language Lexp, by adding in the symbols “+”, “·”, “exp”, “<”, “0”, and “1”. Of course, these come with various syntactic rules that reflect the fact that “+” is a binary operation, “exp” is a function, and so on. For instance, these rules would allow us to write exp(x + y) = z but would forbid us to write exp(x = y) + z.
Here are three more Lexp-formulas:
(ii) ∀x (x > 0 → ∃y exp(y) = x);
(iii) ∃x x2 = –1;
(iv) ∃y y2 = x.
We interpret these formulas as the assertions “for all positive x, there is a y such that ey = x,” “-1 is a square,” and “x is a square.” The first three formulas above are declarative statements about the structure  exp. Formulas (i) and (ii) are true in
exp. Formulas (i) and (ii) are true in  exp, while (iii) is false. Formula (iv) is different because x is a free variable: thus, it expresses a property of x. (For instance, it is true if x = 8, but false if x = -7.) A sentence is defined to be a formula with no free variables. If
exp, while (iii) is false. Formula (iv) is different because x is a free variable: thus, it expresses a property of x. (For instance, it is true if x = 8, but false if x = -7.) A sentence is defined to be a formula with no free variables. If  is an
is an  exp-sentence, then
exp-sentence, then  is either true or false in
is either true or false in  exp.
exp.
If  is a formula with free variables x1, . . .,xn, and a1, . . .,an are real numbers, then we write
is a formula with free variables x1, . . .,xn, and a1, . . .,an are real numbers, then we write  exp
exp 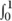
 (a1, . . .,an) if the formula
(a1, . . .,an) if the formula  is true for the particular sequence (a1, . . .,an). We think of the formula as defining the set
is true for the particular sequence (a1, . . .,an). We think of the formula as defining the set
{(a1, . . .,an) ∈  n :
n :  exp
exp 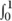
 (a1, . . .,an)},
(a1, . . .,an)},
that is, the set of all sequences (a1, . . .,an) for which the formula is true when you set xi to equal ai for every i. For example, the formula
∃ z (x = z2 + 1 ∧ y = z · exp(exp(z)))
defines the parametrized curve
{(t2 + 1, teet) : t ∈  }.
}.
For another example, one that illustrates an important point, let us consider the structure ( , +, ·, 0, 1): that is, the integers, with addition, multiplication, 0, and 1. The language used to describe this structure is the language of rings,
, +, ·, 0, 1): that is, the integers, with addition, multiplication, 0, and 1. The language used to describe this structure is the language of rings,  rng =
rng =  (+, ·, 0, 1). (The notation here lists the symbols that we add to the basic language
(+, ·, 0, 1). (The notation here lists the symbols that we add to the basic language  0.) The language
0.) The language  rng has no symbol for the usual ordering on
rng has no symbol for the usual ordering on  , but, surprisingly, this ordering can nevertheless be defined in terms of
, but, surprisingly, this ordering can nevertheless be defined in terms of  rng. (To appreciate the nonobviousness of this fact, the reader is encouraged to try to work out why it is true before reading on.)
rng. (To appreciate the nonobviousness of this fact, the reader is encouraged to try to work out why it is true before reading on.)
The trick is to use a well-known theorem due to LAGRANGE [VI.22], which asserts that every nonnegative integer is a sum of four squares. It follows that the statement x 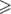 0 can be defined by the formula
0 can be defined by the formula
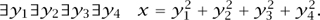
(Of course, we are also using the fact that a negative integer cannot be written as a sum of four squares. Note too that a similar trick would work even if all one knew was that every nonnegative integer was a sum of a hundred squares.) Once one has a way of expressing the statement that x is nonnegative, it is easy to define the symbol “<”. The interesting aspect of this is that the reformulation was not obvious—it depended on a genuine mathematical theorem.
It is important to understand that formulas are restricted in several ways, of which two stand out in particular.
- Formulas are finite. We do not allow formulas like ∀x > 0 (x < l ∨ x < 1 + 1 ∨ x < 1 + 1 + 1 ∨ . . .), which would express the fact that
 has the so-called Archimedean property. (If we did, then it would be much easier to define “<” above.)
has the so-called Archimedean property. (If we did, then it would be much easier to define “<” above.)
- Quantifiers range over elements of the structure, and not subsets. This rules out a “second-order” formula such as
∀S ⊆  (if S is bounded above,
(if S is bounded above,
then S has a least upper bound),
which would express the completeness of  by quantifying over all subsets S of
by quantifying over all subsets S of  . Since we look just at “first-order” formulas, what we are studying is often called first-order logic.
. Since we look just at “first-order” formulas, what we are studying is often called first-order logic.
Now that we have seen some examples of languages, let us discuss them more generally. A language is basically something like  exp or
exp or  rng above: that is, a set of symbols (combined with the basic logical symbols) together with some rules concerning their use. If
rng above: that is, a set of symbols (combined with the basic logical symbols) together with some rules concerning their use. If  is a language, then an
is a language, then an  -structure is a mathematical structure in which all the sentences of
-structure is a mathematical structure in which all the sentences of  can be interpreted. (This concept will become clearer in a moment, when we give a couple of examples.) An
can be interpreted. (This concept will become clearer in a moment, when we give a couple of examples.) An  -theory T is just a set of
-theory T is just a set of  -sentences, which one can think of as axioms that an
-sentences, which one can think of as axioms that an  -structure might or might not satisfy. A model of T is then an
-structure might or might not satisfy. A model of T is then an  -structure
-structure 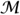 in which all the sentences of T, suitably interpreted, are true. For instance, the structure was a model for the formulas (i) and (ii) of the language
in which all the sentences of T, suitably interpreted, are true. For instance, the structure was a model for the formulas (i) and (ii) of the language  exp that we discussed earlier. (Another model for the same two formulas would be one in which we replaced the exponential function by the function 2x and interpreted “exp” as referring to that function instead.)
exp that we discussed earlier. (Another model for the same two formulas would be one in which we replaced the exponential function by the function 2x and interpreted “exp” as referring to that function instead.)
The justification for the word “theory” is clearer in another example, the language of GROUPS [I.3 §2.1],  grp =
grp =  (ο, e). Here, ο is a binary operation symbol and e is a constant. We might look at the theory Tgrp consisting of the sentences
(ο, e). Here, ο is a binary operation symbol and e is a constant. We might look at the theory Tgrp consisting of the sentences
(i) ∀ x ∀ y ∀ z x ο (y ο z) = (x ο y) ο z;
(ii)∀ x x ο e = e ο x = x;
(iii)∀ x ∃ y x ο y = y ο x = e;
which are the usual axioms for groups.
In order to interpret this language in some mathematical structure 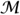 we need
we need 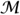 to consist of a set M, a binary operation f : M2 → M, and an element a ∈ M. We then interpret “ο” as referring to f, “e” as referring to the element a, and quantification as being over the set M. Thus, for example, the interpretation of (iii) is that for every x in M there exists a y in M such that f(x, y) = a. Under this interpretation of the symbols of
to consist of a set M, a binary operation f : M2 → M, and an element a ∈ M. We then interpret “ο” as referring to f, “e” as referring to the element a, and quantification as being over the set M. Thus, for example, the interpretation of (iii) is that for every x in M there exists a y in M such that f(x, y) = a. Under this interpretation of the symbols of  grp, the structure
grp, the structure 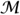 becomes an
becomes an  grp-structure. This
grp-structure. This  grp-structure is a model of Tgrp if in addition the sentences (i), (ii), and (iii) are all true. Since sentences (i)-(iii) are the axioms for groups, a model of Tgrp is nothing other than a group.
grp-structure is a model of Tgrp if in addition the sentences (i), (ii), and (iii) are all true. Since sentences (i)-(iii) are the axioms for groups, a model of Tgrp is nothing other than a group.
We say that an  -sentence
-sentence  is a logical consequence of a theory T, and write T
is a logical consequence of a theory T, and write T 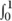
 , if
, if  is true in every model of T. That is, T
is true in every model of T. That is, T 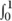
 if
if  is true in every structure in which all the sentences of T are true. Thus, the symbol “
is true in every structure in which all the sentences of T are true. Thus, the symbol “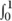 ” has two different meanings, according to whether there is a structure or a theory on the left-hand side. However, these two meanings are closely related in that they are both concerned with truth in models:
” has two different meanings, according to whether there is a structure or a theory on the left-hand side. However, these two meanings are closely related in that they are both concerned with truth in models: 
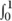
 means that
means that  is true in the model
is true in the model 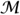 , and T
, and T 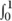
 , as we have just said, means that
, as we have just said, means that  is true in every possible model of T. Either way, the symbol “
is true in every possible model of T. Either way, the symbol “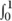 ” stands for a “semantic” notion of entailment.
” stands for a “semantic” notion of entailment.
Returning to the example of groups, if  is a sentence in
is a sentence in  grp, then Tgrp
grp, then Tgrp 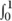
 if and only if
if and only if  is true for every group. So, for instance,
is true for every group. So, for instance,
Tgrp 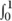 ∀ x ∀ y ∀ z (x y ≠ x z ∨ y = z),
∀ x ∀ y ∀ z (x y ≠ x z ∨ y = z),
because if x,y, and z are elements of any group and x y = x z, then we can multiply both sides on the left by the inverse of x to deduce that y = z.
We can now describe some of the basic problems in logic.
(i) Given an  -theory T, can we decide if a sentence
-theory T, can we decide if a sentence  is a logical consequence of T, and if so how?
is a logical consequence of T, and if so how?
(ii) Given an interesting mathematical structure, like  exp, or (
exp, or (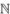 , +, ·, 0, 1), or the complex field, and a language
, +, ·, 0, 1), or the complex field, and a language  that describes the structure, can we determine which
that describes the structure, can we determine which  -sentences are true of the structure?
-sentences are true of the structure?
(iii) Given a structure described by a language, do the subsets of the structure that can be defined in the language have special properties? Are they in some sense “simple”? For example, earlier we saw how to use  exp to define a certain curve in the plane. Now consider a very complicated set such as a CANTOR SET [III.17] or the MANDELBROT SET [IV.14 §2.8]. Is it possible to prove that these sets cannot be defined in
exp to define a certain curve in the plane. Now consider a very complicated set such as a CANTOR SET [III.17] or the MANDELBROT SET [IV.14 §2.8]. Is it possible to prove that these sets cannot be defined in  exp because they are “too complex” in some sense?
exp because they are “too complex” in some sense?
2 Completeness and Incompleteness
Let T be an  -theory and let
-theory and let  be an
be an  -sentence. To show that T
-sentence. To show that T 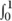
 we must show that
we must show that  holds in every model of T. Checking all models of T sounds like a daunting task, but fortunately it is not necessary, since instead we can use a proof. One of the first tasks in mathematical logic is to say precisely what this means.
holds in every model of T. Checking all models of T sounds like a daunting task, but fortunately it is not necessary, since instead we can use a proof. One of the first tasks in mathematical logic is to say precisely what this means.
Suppose, then, that  is some language and that T is a set of sentences in
is some language and that T is a set of sentences in  , i.e., an
, i.e., an  -theory. Suppose also that
-theory. Suppose also that  is a formula of
is a formula of  . Informally speaking, a proof of
. Informally speaking, a proof of  assumes the statements of T and ends up establishing
assumes the statements of T and ends up establishing  . We express this idea formally as follows. A proof of
. We express this idea formally as follows. A proof of  from T is a finite sequence of
from T is a finite sequence of  -formulas ψ1, . . .,ψm (which one can think of as the lines of the proof) with the following properties:
-formulas ψ1, . . .,ψm (which one can think of as the lines of the proof) with the following properties:
(i) each ψi is either a logical axiom, or a sentence of T, or a formula that follows from the previous formulas ψ1, . . .,ψi-1 by means of simple logical rules;
(ii) ψm =  .
.
We shall not say precisely what a “simple logical rule” is, but three examples are
- from
 and ψ it follows that
and ψ it follows that  ∧ ψ
∧ ψ
- from
 ∧ ψ it follows that
∧ ψ it follows that 
- from
 (x) it follows that ∃V
(x) it follows that ∃V  (V)
(V)
The other possible rules are similarly elementary.
There are three points about proofs that need to be stressed. The first is that they are finite, which may seem too obvious to mention but is important because it has a number of consequences that are not obvious. The second is that proof systems have to be sound: if there is a proof of  from T, then
from T, then  is true in every model of T. To put this more succinctly, let us introduce the notation T
is true in every model of T. To put this more succinctly, let us introduce the notation T 
 for the statement that there is a proof of
for the statement that there is a proof of  from T. Then soundness is the assertion that if T
from T. Then soundness is the assertion that if T 
 then T
then T 
 . This is why we can prove that
. This is why we can prove that  is true in every model of T by finding a proof rather than by looking at all the models. The third point is that it is easy to check whether a sequence of sentences is a proof. More precisely, there is an algorithm that can look at a sequence ψ1, . . .,ψm and decide whether it really is a proof of
is true in every model of T by finding a proof rather than by looking at all the models. The third point is that it is easy to check whether a sequence of sentences is a proof. More precisely, there is an algorithm that can look at a sequence ψ1, . . .,ψm and decide whether it really is a proof of  from T.
from T.
It is not too surprising that if ϕ can be proved from T, then ϕ is true in all models of T. Much more remarkable is that the converse is also true: if ϕ cannot be proved from T, then there must be a model of T in which ϕ is false. This tells us that two very different notions—the finitistic, syntactic notion of “proof” and the semantic notion of “logical consequence,” which concerns truth in models—always agree. This result is known as Gödel’s completeness theorem. Here is its formal statement.
Theorem. Let T be an  -theory and let ϕ be an
-theory and let ϕ be an  -sentence. Then T
-sentence. Then T  ϕ if and only if T
ϕ if and only if T 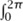 ϕ.
ϕ.
Suppose that T is a simple theory like Tgrp, where there is an algorithm to decide whether a sentence is in T. (In the case of Tgrp this algorithm is particularly simple, but some theories might have infinitely many sentences.) We could write a computer program which, given a formula ϕ as its input, would systematically generate all possible proofs σ from T and check to see whether σ was a proof of ϕ. If such a program finds a proof of ϕ, then it halts and tells us that T  ϕ. We say that {ϕ : T
ϕ. We say that {ϕ : T  ϕ} is recursively enumerable.
ϕ} is recursively enumerable.
However, one might hope for more. If T 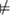 ϕ, our program above will go on searching forever, so it will never tell us that there is no proof of ϕ. We say that an
ϕ, our program above will go on searching forever, so it will never tell us that there is no proof of ϕ. We say that an  -theory T is decidable if there is a computer program which, when given an
-theory T is decidable if there is a computer program which, when given an  -sentence ϕ as input, will always halt and tell us, one way or another, whether T
-sentence ϕ as input, will always halt and tell us, one way or another, whether T  ϕ. Such a program would have to be cleverer than the one that just checks all possible proofs σ, and unfortunately such a program does not have to exist: as GÖDEL [VI.92] proved in his famous INCOMPLETENESS THEOREM [V.15], many important theories are undecidable. Here is a first version of his theorem, concerning the theory of the natural numbers (or theory of ℕ for short), which means the set of all sentences in the language
ϕ. Such a program would have to be cleverer than the one that just checks all possible proofs σ, and unfortunately such a program does not have to exist: as GÖDEL [VI.92] proved in his famous INCOMPLETENESS THEOREM [V.15], many important theories are undecidable. Here is a first version of his theorem, concerning the theory of the natural numbers (or theory of ℕ for short), which means the set of all sentences in the language  rng that are true of the structure (ℕ, +, ·, 0, 1).
rng that are true of the structure (ℕ, +, ·, 0, 1).
Theorem. The theory of the natural numbers is undecidable.
At first, this might seem rather strange: after all, if T is the theory of ℕ, then T contains all true sentences about ℕ. So a sentence ϕ is provable from T if and only if it has a one-line proof (the line being ϕ itself). However, this does not make ϕ decidable, because the theory T is very complicated and there is no algorithm for deciding whether ϕ belongs to T.
One approach to proving the incompleteness theorem is to associate a natural number with each computer program in such a way that statements about programs can be recast as statements about natural numbers. The theory of ℕ then determines whether a program P halts on input x, thus solving what is known as the halting problem. Since the halting problem was shown by TURING [VI.94] to be undecidable (a sketch of the proof can be found in THE INSOLUBILITY OF THE HALTING PROBLEM [V.20]), it follows that the theory of ℕ is undecidable.
How can we understand the theory of ℕ? One might hope to find a much smaller theory that yielded the same true sentences. That is, we could try to find a simple set of axioms about ℕ that we know are true and hope that every true sentence follows from these axioms. A good candidate is first-order Peano arithmetic, or PA. This is a theory in the language  (+, ·, 0, 1) that involves a few simple axioms about addition and multiplication, such as
(+, ·, 0, 1) that involves a few simple axioms about addition and multiplication, such as
∀x∀y x · (y + 1) = x · y + x,
together with axioms for induction.
Why do we need more than one axiom of induction? The reason is that the obvious statement that expresses the principle of mathematical induction, namely
∀ A (0 ∈ A ∧ ∀ x x ∈ A → x + ∈ A)→ ∀x x ∈ A,
is not a first-order sentence, because the quantifier is applied to all subsets A of ℕ. (It is also not a sentence in  rng since it uses the symbol “∈”, but this is a less fundamental problem.) To get around this difficulty, one has a separate axiom of induction for each formula ϕ. It is the assertion that
rng since it uses the symbol “∈”, but this is a less fundamental problem.) To get around this difficulty, one has a separate axiom of induction for each formula ϕ. It is the assertion that
[ϕ(0) ∧ ∀x (ϕ(x) → ϕ(x + 1))] → ∀x ϕ(x).
In words, this says that if ϕ(0) is true and ϕ(x + 1) is true whenever ϕ(x) is true, then ϕ(x) is true for every x in ℕ.
Most of number theory can be formalized in PA and one might hope that PA 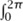 ϕ for every ϕ that is true in ℕ. Sadly, this is not true. Here is a second version of Gödel’s incompleteness theorem. Recall that the notation ℕ
ϕ for every ϕ that is true in ℕ. Sadly, this is not true. Here is a second version of Gödel’s incompleteness theorem. Recall that the notation ℕ  ψ means simply that ψ is true in ℕ.
ψ means simply that ψ is true in ℕ.
Theorem. There is a sentence ψ such that ℕ  ψ but PA
ψ but PA 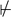 ψ.
ψ.
Another way to state this result is to say that there is a sentence ψ such that PA 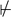 ψ and PA
ψ and PA 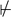 ¬ ψ. To see that this is an equivalent statement, let ψ be any sentence. Then precisely one of ψ and ¬ψ is true. Therefore, if the theorem is false, then PA must prove either ψ or ¬ψ. But this means that we can decide which by simply going through all possible proofs in PA until we find a proof of ψ or a proof of ¬ψ.
¬ ψ. To see that this is an equivalent statement, let ψ be any sentence. Then precisely one of ψ and ¬ψ is true. Therefore, if the theorem is false, then PA must prove either ψ or ¬ψ. But this means that we can decide which by simply going through all possible proofs in PA until we find a proof of ψ or a proof of ¬ψ.
Gödel’s original example of a true but unprovable sentence was a self-referential sentence that effectively asserted
“I am not provable from PA.”
More precisely, he found a sentence ψ for which he was able to show that ψ is true in ℕ if and only if ψ is not provable from PA. With more work he showed that there is a sentence that asserts
“PA is consistent”
that is unprovable from PA. The somewhat artificial and metamathematical nature of these sentences might lead one to hope that all “mathematically interesting” sentences about ℕ are settled by PA. However, more recent work has shown that even this is a forlorn hope, since there are undecidable statements related to RAMSEY’S THEOREM [IV.19 §2.2] in finite combinatorics.
Undecidability also appears in number theory in a very basic way. Hilbert’s tenth problem asked if there is an algorithm to decide whether a polynomial p (X1, . . . , Xn) with integer coefficients has an integer zero. Davis, Matijasevic, Putnam, and Robinson showed that the answer is no.
Theorem. For any recursively enumerable S ⊆ ℕ there is n > 0 and p (X, Y1, . . . , Yn) ∈ ℤ[X, Y1, . . . , Yn] such that m ∈ S if and only if p(m, Y1, . . . , Yn) has an integer zero.
Since the halting problem provides an undecidable recursively enumerable set, the answer to Hilbert’s tenth problem is no. An important open question is whether there is an algorithm to decide if a polynomial with rational coefficients has a rational zero. Hilbert’s tenth problem is also discussed in THE INSOLUBILITY OF THE HALTING PROBLEM [V.20], and other interesting examples of undecidability can be found in GEOMETRIC AND COMBINATORIAL GROUP THEORY [IV.10].
3 Compactness
A theory T is called satisfiable if there are structures that satisfy all of the sentences in T (that is, if T has a model), and we call T consistent if we cannot derive a contradiction from T. Since our proof system is sound, any satisfiable theory is consistent. On the other hand if T is not satisfiable, then every sentence ϕ is a logical consequence of T, for the trivial reason that there are no models of T in which ϕ is required to be true. But the completeness theorem then tells us that T 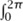 ϕ for every ϕ. Choosing ϕ to be some contradictory statement, of the form ψ ∧ ¬ψ, for instance, we see that T is inconsistent. This way of reformulating the completeness theorem has the following simple consequence, called the compactness theorem, which turns out to be surprisingly important, as we shall see.
ϕ for every ϕ. Choosing ϕ to be some contradictory statement, of the form ψ ∧ ¬ψ, for instance, we see that T is inconsistent. This way of reformulating the completeness theorem has the following simple consequence, called the compactness theorem, which turns out to be surprisingly important, as we shall see.
Theorem. If every finite subset of T is satisfiable, then T is satisfiable.
The reason this is true is that if T is not satisfiable then it is inconsistent (as we have just seen), which means that a contradiction can be proved from T. Since this proof, like all proofs, must be finite, it involves only finitely many sentences from T. Therefore, T has a finite subset that implies a contradiction, which contradicts our assumption that all finite subsets of T are satisfiable.
Although the compactness theorem is an easy consequence of the completeness theorem, it has many immediate intriguing consequences and lies at the heart of many constructions in model theory. Here are two simple applications that show that theories have many models that you might not expect. If M is some  -structure, let us write Th(M) for the theory of M: that is, for the set of all
-structure, let us write Th(M) for the theory of M: that is, for the set of all  -sentences that are true in M. We also extend our earlier notation M
-sentences that are true in M. We also extend our earlier notation M  ϕ from single formulas to collections of formulas, so if M is an
ϕ from single formulas to collections of formulas, so if M is an  -structure and T is an
-structure and T is an  -theory, then M
-theory, then M  T means that every sentence of T is true in M, or in other words that M is a model of T.
T means that every sentence of T is true in M, or in other words that M is a model of T.
Corollary. There exists an  exp-structure M containing an infinite element a (whichmeans that a > 1, a > 1+1, a > 1 + 1 + 1, etc.), such that M
exp-structure M containing an infinite element a (whichmeans that a > 1, a > 1+1, a > 1 + 1 + 1, etc.), such that M  Th( ℝexp).
Th( ℝexp).
That is, there is a structure M in which all the true first-order statements about the structure ℝexp are still true, but M is different from ℝexp because it contains an infinite element. To prove this, we add one more constant symbol c to our language and consider the theory T that consists of all the statements of Th( ℝexp) (that is, all true statements about ℝexp), together with the infinite sequence of statements c > 1, c > 1 + 1, c > 1 + 1 + 1, and so on. If Δ is any finite subset of T, then we can make ℝ a model of Δ simply by interpreting c as a sufficiently large real number—large enough to satisfy all the statements of the form c > 1 + 1 + · · · + 1 that belong to Δ. Since we can model every finite subset Δ of T, the compactness theorem tells us that we can model T itself. If M  T, then the element named by c must be infinite
T, then the element named by c must be infinite
The element 1/a will be an infinitesimal element of M (which means that it satisfies statements that effectively say that it is smaller than 1/n for every positive integer n). This observation is the first step toward a rigorous development of calculus with infinitesimals.
For another example, let  rng =
rng =  (+, ·, 0, 1) be the language of rings. Let T be the set of
(+, ·, 0, 1) be the language of rings. Let T be the set of  -sentences that are true in every finite field. We call T the theory of finite fields. Recall that a field is said to have characteristic p if p is the smallest positive integer (which has to be prime) such that 1 + 1 + · · · + 1 = 0 in the field, where the number of 1s in the sum is p. If there is no such p, then the field is said to have characteristic zero. Thus, the fields ℚ, ℝ, and ℂ all have characteristic zero.
-sentences that are true in every finite field. We call T the theory of finite fields. Recall that a field is said to have characteristic p if p is the smallest positive integer (which has to be prime) such that 1 + 1 + · · · + 1 = 0 in the field, where the number of 1s in the sum is p. If there is no such p, then the field is said to have characteristic zero. Thus, the fields ℚ, ℝ, and ℂ all have characteristic zero.
Corollary. There is a field F with characteristic zero such that F 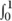 T.
T.
This result tells us that there is no possible set of axioms that characterizes the finite fields: given any set of statements that are true in all finite fields, there is an infinite field in which they are also all true. To prove it, we look at the theory T′ that consists of T together with the statements 1 + 1 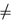 0, 1 + 1 + 1
0, 1 + 1 + 1 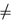 0, and so on. Any finite set of statements in T′ will be true of a finite field of sufficiently large characteristic, and thus satisfiable. By the compactness theorem T′ is satisfiable, but a model of T clearly has to have characteristic zero.
0, and so on. Any finite set of statements in T′ will be true of a finite field of sufficiently large characteristic, and thus satisfiable. By the compactness theorem T′ is satisfiable, but a model of T clearly has to have characteristic zero.
The compactness theorem can sometimes be used to show the existence of interesting algebraic bounds. The next result allows us to deduce from HILBERT’S NULLSTELLENSATZ [V.17] a stronger “quantitative version.” It is our first example of a statement that does not appear to be logical in nature but which can be proved using logic. Recall that a field is algebraically closed if every polynomial with coefficients in the field has a root in the field. (THE FUNDAMENTAL THEOREM OF ALGEBRA [V.13] is the assertion that ℂ is an algebraically closed field.)
Proposition. For any three positive integers n, m, d there is a positive integer l such that if K is an algebraically closed field and f1, . . . , fm are polynomials in n variables with coefficients in K, degree at most d and no common zero, then there are polynomials g1, . . . ,gm of degree at most l such that Σgifi = 1.
Hilbert’s Nullstellensatz itself is the same statement but without the extra information about the degrees of the polynomials gi.
To see how the proposition is proved, we will restrict our attention to the case n = d = 2. This is just for notational simplicity: the proof is almost identical in larger cases. For each i between 1 and m let
Fi = aiX2 + biY2 + ciXY + diX + eiY + fi.
For each k write down a formula ϕk that asserts that there are no polynomials G1, . . . , Gm with degree at most k such that 1 = Σ FiGi. Let T be the theory of algebraically closed fields with the formulas ϕ1, ϕ2, and the assertion that the polynomials F1, . . . , Fm have no common zero. If there is no positive integer l satisfying the conclusion of the proposition, then every finite subset of T is satisfiable. Hence, by the compactness theorem, T is satisfiable. If K 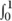 T, then F1, . . . , Fm are polynomials over an algebraically closed field with no common zero, but it is impossible to find polynomials G1, . . . , Gm such that ΣGiFi = 1. This contradicts Hilbert’s Nullstellensatz.
T, then F1, . . . , Fm are polynomials over an algebraically closed field with no common zero, but it is impossible to find polynomials G1, . . . , Gm such that ΣGiFi = 1. This contradicts Hilbert’s Nullstellensatz.
Notice that in the above argument we did not say anything about the dependence of l on n, m, and d. This is because the proof does not actually find a bound: it merely shows that some sort of bound must exist. However, good explicit bounds were recently discovered—see ALGEBRAIC GEOMETRY [IV.4] for more details.
4 The Complex Field
A surprising counterpoint to Gödel’s incompleteness theorem is a result of TARSKI [VI.87], which states that the theories of the fields of real and complex numbers are decidable. The key to these results is a method known as quantifier elimination. If we have a formula without quantifiers that concerns the natural numbers, then it is easy to decide whether it is true or false. The negative solution to Hilbert’s tenth problem shows that as soon as we start adding existential quantifiers (as we do if, for example, we assert that a polynomial has a zero), then we leave the realm of decidability.
Thus, if we want to show that a formula is decidable, it will be very useful if we can find an equivalent formula that does not have quantifiers. And in some settings, this turns out to be possible. For example, let ϕ(a, b, c) be the formula
∃x ax2 + bx + c = 0.
The usual rule for solving quadratics tells us that, as long as a ≠ 0, this is true in  if and only if b2
if and only if b2 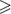 4ac. Therefore,
4ac. Therefore, 
 ϕ(a, b, c) if and only if
ϕ(a, b, c) if and only if
[(a ≠ 0 ∧ b2 – 4ac 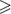 0) ∨ (a = 0 ∧ (b ≠ 0 ∨ c = 0))].
0) ∨ (a = 0 ∧ (b ≠ 0 ∨ c = 0))].
As for the complex numbers, it is easy to see that 
 ϕ(a, b, c) if and only if
ϕ(a, b, c) if and only if
a ≠ 0 ∨ b ≠ 0 ∨ c = 0.
In either case, ϕ is equivalent to a formula with no quantifiers.
For a second example, let ϕ(a, b, c, d) be the formula
∃x∃y∃u∃v (xa + yc = 1 ∧ xb + yd = 0 ∧ ua + vc = 0 ∧ ub + vd = 1).
The formula ϕ(a, b, c, d) is the obvious way of asserting that the matrix 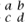 is invertible. However, by the DETERMINANT [III.15] test, we know that, for any field F, F
is invertible. However, by the DETERMINANT [III.15] test, we know that, for any field F, F  ϕ(a, b, c, d) if and only if ad – bc ≠ 0. Thus the existence of an inverse can be expressed by the quantifier-free formula ad – bc ≠ 0.
ϕ(a, b, c, d) if and only if ad – bc ≠ 0. Thus the existence of an inverse can be expressed by the quantifier-free formula ad – bc ≠ 0.
Tarski proved that we can always eliminate quantifiers in algebraically closed fields.
Theorem. For any 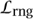 -formula ϕ there is a quantifier-free formula ψ such that ϕ is equivalent to ψ in every algebraically closed field.
-formula ϕ there is a quantifier-free formula ψ such that ϕ is equivalent to ψ in every algebraically closed field.
Furthermore, Tarski gave an explicit algorithm for eliminating the quantifiers.
The equivalent quantifier-free formulas above were both finite Boolean combinations of formulas of the form p(v1, . . .,vn) = q(v1, . . ., vn), where p and q are polynomials in n variables with integer coefficients. It is not hard to see that this is true of any quantifier-free  -formula. It follows that a quantifier-free
-formula. It follows that a quantifier-free 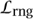 -sentence is particularly simple: if no free variables are allowed and no quantifiers are allowed, then there cannot be any variables! Therefore, the polynomials p and q have to be constant, which means that a quantifier-free
-sentence is particularly simple: if no free variables are allowed and no quantifiers are allowed, then there cannot be any variables! Therefore, the polynomials p and q have to be constant, which means that a quantifier-free 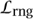 -sentence is a finite Boolean combination of formulas of the form k = l (where this should be regarded as an abbreviation for 1 + 1 + · · · + 1 = 1 + 1 + · · · + 1, with k 1s on the left-hand side and l 1s on the right-hand side).
-sentence is a finite Boolean combination of formulas of the form k = l (where this should be regarded as an abbreviation for 1 + 1 + · · · + 1 = 1 + 1 + · · · + 1, with k 1s on the left-hand side and l 1s on the right-hand side).
This leads to the decidability result. If we want to know whether 
 ϕ, then we use Tarski’s algorithm to convert ϕ into an equivalent quantifier–free sentence. But the very simple form of such sentences makes their truth or falsity easy to decide.
ϕ, then we use Tarski’s algorithm to convert ϕ into an equivalent quantifier–free sentence. But the very simple form of such sentences makes their truth or falsity easy to decide.
In the remainder of this section, we shall discuss a number of other consequences of Tarski’s theorem. The first is that sentences in the language 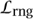 cannot distinguish between different algebraically closed fields of the same characteristic. That is, if ϕ is any
cannot distinguish between different algebraically closed fields of the same characteristic. That is, if ϕ is any 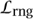 -sentence that is true for some algebraically closed field of characteristic p (where p is allowed to be zero), then it is true in every algebraically closed field of characteristic p.
-sentence that is true for some algebraically closed field of characteristic p (where p is allowed to be zero), then it is true in every algebraically closed field of characteristic p.
To see why this is true, let K and F be two algebraically closed fields of characteristic p, and suppose that K  ϕ (or in other words that ϕ is true of K). Let k be the field ℚ if the characteristic is zero and the field with p elements otherwise. Tarski’s theorem tells us that there is a quantifier–free sentence ϕ that is equivalent to ϕ in all algebraically closed fields of characteristic p. However, the extremely simple nature of the quantifier–free sentences of
ϕ (or in other words that ϕ is true of K). Let k be the field ℚ if the characteristic is zero and the field with p elements otherwise. Tarski’s theorem tells us that there is a quantifier–free sentence ϕ that is equivalent to ϕ in all algebraically closed fields of characteristic p. However, the extremely simple nature of the quantifier–free sentences of 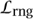 means that their truth or falsity in any given field depends only on the elements 0, 1, 1 + 1, and so on. Therefore,
means that their truth or falsity in any given field depends only on the elements 0, 1, 1 + 1, and so on. Therefore,
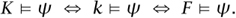
Since K  ϕ and ϕ and ψ are equivalent in all algebraically closed fields of characteristic p, it follows that F
ϕ and ϕ and ψ are equivalent in all algebraically closed fields of characteristic p, it follows that F  ϕ as well.
ϕ as well.
A consequence of this theorem is that an 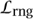 -sentence ϕ is true of the complex numbers if and only if it is true of the algebraic numbers ℚalg. (Recall that these are all roots of polynomials with integer coefficients. As one would expect, the algebraic numbers form an algebraically closed field, though this is not a wholly obvious fact.) Thus, rather surprisingly, if we wish to prove something about ℚalg, we have the option of working in
-sentence ϕ is true of the complex numbers if and only if it is true of the algebraic numbers ℚalg. (Recall that these are all roots of polynomials with integer coefficients. As one would expect, the algebraic numbers form an algebraically closed field, though this is not a wholly obvious fact.) Thus, rather surprisingly, if we wish to prove something about ℚalg, we have the option of working in  and using the methods of complex analysis; similarly, if we want to prove something about
and using the methods of complex analysis; similarly, if we want to prove something about  we can, if it makes things easier, work in ℚalg and use number-theoretic methods.
we can, if it makes things easier, work in ℚalg and use number-theoretic methods.
Combining these ideas with the completeness theorem gives another useful tool. If ϕ is any 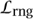 -sentence, then the following are equivalent:
-sentence, then the following are equivalent:
(i) ϕ is true in every algebraically closed field of characteristic zero;
(ii) for some m > 0, ϕ is true in every algebraically closed field of characteristic p > m;
(iii) there are arbitrarily large p such that ϕ is true in some algebraically closed field of characteristic p.
Let us see why this is so. Suppose first that ϕ is true in every algebraically closed field of characteristic 0. The completeness theorem then implies that there is a proof of ϕ from the axioms for algebraically closed fields combined with the sentences 1 ≠ 0, 1 + 1 ≠ 0, 1 + 1 + 1 ≠ 0, and so on. Since proofs are finite sequences of formulas, there must be some m such that the proof used only the first m of these sentences (not necessarily all of them). If p is some prime bigger than m, then this proof shows that ϕ holds in algebraically closed fields of characteristic p, since all the sentences we used are true in such fields.
We have just shown that (i) implies (ii). It is obvious that (ii) implies (iii). To see that (iii) implies (i), let us suppose that (i) fails, so that there is an algebraically closed field of characteristic zero in which ¬ϕ is true. Then, by the principle we proved earlier, ¬ϕ is true in every algebraically closed field of characteristic zero. Thus, since (i) implies (ii), there is an m such that ¬ϕ is true in every algebraically closed field of characteristic p > m. Therefore (iii) fails.
An interesting application of this theorem was found by Ax. It is another example of a statement that has nothing to do with logic, but which can be proved using logical tools. It is perhaps more striking than the previous example because in this case one does not even feel with hindsight that the statement did after all have some logical content.
Theorem. If a polynomial map from  n to
n to  n is an injection, then it must also be a surjection.
n is an injection, then it must also be a surjection.
The basic thought behind the proof of this result is very simple indeed: what is remarkable is that it is of any help. It is the observation that if k is a finite field, then every injective polynomial map from kn to kn is a surjection. This is true because every injection from a finite set to itself is automatically a surjection.
How do we exploit this observation? Well, the previous results tell us that, in several situations, statements are true for one field if and only if they are true for another. We shall use these results to transfer our problem from  , where it is hard, to a finite field k, where it is trivial. The first step is a routine exercise: one shows that for each positive integer d there is a sentence ϕd in
, where it is hard, to a finite field k, where it is trivial. The first step is a routine exercise: one shows that for each positive integer d there is a sentence ϕd in 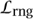 that expresses the fact that every injective polynomial map from Fn to Fn, with the n polynomials all of degree at most d, is surjective. We would like to prove that all the sentences ϕd are true when F =
that expresses the fact that every injective polynomial map from Fn to Fn, with the n polynomials all of degree at most d, is surjective. We would like to prove that all the sentences ϕd are true when F =  .
.
The equivalences in the previous theorem imply that it is enough to prove that the sentences ϕd are true when F is the field 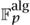 , the algebraic closure of the p-element field. (It can be shown that any field F is contained in an algebraically closed field. Roughly speaking, the algebraic closure of F is the smallest algebraically closed field that contains F.) Suppose, then, that some ϕd fails for
, the algebraic closure of the p-element field. (It can be shown that any field F is contained in an algebraically closed field. Roughly speaking, the algebraic closure of F is the smallest algebraically closed field that contains F.) Suppose, then, that some ϕd fails for 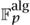 . Then there must be an injective polynomial map f from (
. Then there must be an injective polynomial map f from (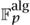 )n to (
)n to (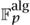 )n that is not surjective. Since every finite subset of
)n that is not surjective. Since every finite subset of 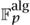 is contained in a finite subfield, there is a finite subfield k such that all the n polynomials used to define f have coefficients in k, from which it follows that f maps kn to kn. Moreover, by enlarging k if necessary, we can ensure that there is an element of kn that is not in the image of f. But now we have succeeded in transferring ourselves to a finite field: this function f : kn → kn is an injection between finite sets that is not a surjection, which is a contradiction.
is contained in a finite subfield, there is a finite subfield k such that all the n polynomials used to define f have coefficients in k, from which it follows that f maps kn to kn. Moreover, by enlarging k if necessary, we can ensure that there is an element of kn that is not in the image of f. But now we have succeeded in transferring ourselves to a finite field: this function f : kn → kn is an injection between finite sets that is not a surjection, which is a contradiction.
Quantifier elimination has other useful applications. Let F be a field, let K be a subfield of F, let ϕ (v1, . . ., vn) be a quantifier–free formula, and let a1, . . ., an be elements of K. Since, as we have already mentioned, quantifier–free formulas are just Boolean combinations of equalities between polynomials, the statement ϕ(a1, . . ., an) involves just the elements of K, and is therefore true in K if and only if it is true in F. By quantifier elimination, if K and F are algebraically closed, then the same is true for all formulas ϕ, and not just those that are quantifier free. From this observation we can prove the “weak version” of Hilbert’s Nullstellensatz. (For the proof, we shall need to assume a certain degree of familiarity with the basics of RING THEORY [III.81]. We shall also write K[X] for the polynomial ring K[X1, . . ., Xn] and 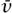 for the n-tuple (v1, . . ., vn).)
for the n-tuple (v1, . . ., vn).)
Proposition. Suppose that K is an algebraically closed field, P is a prime ideal in K [X], and g is a polynomial in K[X] that does not belong to P. Then there is some a = (a1, . . ., an) in Kn such that f (a) = 0 for every f that belongs to P, and such that g (a) ≠ 0.
Proof. Let F be the algebraic closure of the fraction field of the integral domain K[X]/P. We can view F as an extension field of K with a natural homomorphism η : K[X] → F. Let bi = η(Xi) and let b ∈ Fn be the element (b1,. . ., bn). Then f(b) = 0 for all f ∈ P and g(b) ≠ 0. We would like to find such an element in K. Since ideals in polynomial rings are finitely generated, we can find polynomials f1, . . ., fm that generate P. The sentence
∃v1 ··· ∃vn(f1 (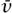 ) = ··· = fm(
) = ··· = fm(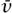 ) = 0 ∧ g(
) = 0 ∧ g(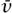 ) ≠ 0)
) ≠ 0)
is true in F. Thus it is also true in K and we can find a ∈ Kn such that each f ∈ P vanishes at a but g(a) ≠ 0. 
Notice that the above proof has the same basic structure as the result about polynomial maps on  n. The idea was to come up with a different field, in this case F, where the result was easy to prove, and use logical ideas to deduce the result for the field we were originally interested in, in this case K.
n. The idea was to come up with a different field, in this case F, where the result was easy to prove, and use logical ideas to deduce the result for the field we were originally interested in, in this case K.
5 The Reals
Quantifier elimination in the language of rings does not work in the field of real numbers. For instance, the formula
∃y x = y · y,
which asserts “x is a square,” is not equivalent to a quantifier–free formula in the language of rings. Of course, x is a square if and only if x 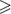 0. So we could eliminate this quantifier if we were prepared to add a symbol for the ordering to our language. An amazing result of Tarski shows that this is the only obstruction to quantifier elimination.
0. So we could eliminate this quantifier if we were prepared to add a symbol for the ordering to our language. An amazing result of Tarski shows that this is the only obstruction to quantifier elimination.
Let  or be the language of ordered rings, which is the language of rings with the addition of the symbol “<” for an ordering. Which
or be the language of ordered rings, which is the language of rings with the addition of the symbol “<” for an ordering. Which  or-sentences are true in the real field? Some of the properties of
or-sentences are true in the real field? Some of the properties of  that we can formalize in
that we can formalize in  or include:
or include:
(i) the axioms for ordered fields, such as the sentence

(ii) the intermediate-value property for polynomials, which states that if p(x) is a polynomial and there exist a and b such that a < b and p(a) < 0 < p(b), then there exists a real number c such that a < c < b and p(c) = 0.
The intermediate-value property is expressed not by just one sentence, but by the infinite sequence of sentences
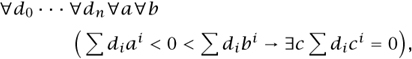
one for each positive integer n.
An ordered field that satisfies the intermediate-value property is called a real closed field. It turns out that an equivalent way of axiomatizing real closed fields is as ordered fields for which every positive element is a square and every polynomial of odd degree has a zero. Tarski’s theorem is the following statement.
Theorem. For any  or-formula ϕ there is a quantifier–free
or-formula ϕ there is a quantifier–free  or-formula ψ such that ϕ and ψ are equivalent in every real closed field.
or-formula ψ such that ϕ and ψ are equivalent in every real closed field.
What are the quantifier–free formulas of  or? It turns out (and is not hard to show) that they are finite Boolean combinations of formulas of the form p(v1, . . ., vn) = q (v1 , . . ., vn) and formulas of the form p(v1 , . . ., vn) < q(v1, . . ., vn), where, as in the case of
or? It turns out (and is not hard to show) that they are finite Boolean combinations of formulas of the form p(v1, . . ., vn) = q (v1 , . . ., vn) and formulas of the form p(v1 , . . ., vn) < q(v1, . . ., vn), where, as in the case of 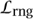 , p and q are polynomials in n and m variables, respectively, with integer coefficients. As for quantifier–free sentences, they are Boolean combinations of sentences of the form k = l and sentences of the form k < l.
, p and q are polynomials in n and m variables, respectively, with integer coefficients. As for quantifier–free sentences, they are Boolean combinations of sentences of the form k = l and sentences of the form k < l.
One consequence of quantifier elimination is the following result, which tells us that every  or statement that is true in
or statement that is true in  can be proved from the real-closed-field axioms. One says that these axioms completely axiomatize the theory of the real field.
can be proved from the real-closed-field axioms. One says that these axioms completely axiomatize the theory of the real field.
Corollary. Let K be a real closed field and let ϕ be an  or-sentence. Then K
or-sentence. Then K  ϕ if and only if
ϕ if and only if 
 ϕ.
ϕ.
To prove this, first use Tarski’s theorem to find a quantifier–free sentence ψ such that ϕ and ψ are equivalent in any real closed field. Every ordered field has characteristic zero and contains the rational numbers as an ordered subfield. Therefore ℚ is a subfield of both K and  . But the very simple nature of quantifier–free sentences in
. But the very simple nature of quantifier–free sentences in  or means that
or means that
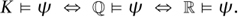
Since ϕ and ψ are equivalent in all real closed fields, it follows that K  ϕ if and only if
ϕ if and only if 
 ϕ.
ϕ.
By the completeness theorem, ϕ is true in every real closed field if and only if we can prove ϕ from the axioms for real closed fields, and ϕ is false in every real closed field if and only if we can prove ¬ϕ from the axioms for real closed fields. It follows that the  or-theory of the real field is decidable. Indeed, if ϕ is true in
or-theory of the real field is decidable. Indeed, if ϕ is true in  , then by the corollary above, it is true in every real closed field, so it has a proof. If ϕ is false in
, then by the corollary above, it is true in every real closed field, so it has a proof. If ϕ is false in  , then ¬ϕ is true in
, then ¬ϕ is true in  , so for the same reason ¬ϕ has a proof. Therefore, to decide whether ϕ is true, one can search through all possible proofs from the axioms of real closed fields until one proves either ϕ or ¬ϕ.
, so for the same reason ¬ϕ has a proof. Therefore, to decide whether ϕ is true, one can search through all possible proofs from the axioms of real closed fields until one proves either ϕ or ¬ϕ.
Let 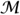 be a mathematical structure consisting of a set M and various other parts such as functions and binary operations. A subset X of M is called definable, with respect to some language
be a mathematical structure consisting of a set M and various other parts such as functions and binary operations. A subset X of M is called definable, with respect to some language  that describes
that describes 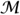 , if there is an
, if there is an  -formula ϕ with a free variable x such that X = {x ∈ M : ϕ(x)}. Quantifier elimination gives us a good geometric understanding of the definable sets. If K is an ordered field, we say that X ⊆ Kn is semialgebraic if it is a finite Boolean combination of sets of the form
-formula ϕ with a free variable x such that X = {x ∈ M : ϕ(x)}. Quantifier elimination gives us a good geometric understanding of the definable sets. If K is an ordered field, we say that X ⊆ Kn is semialgebraic if it is a finite Boolean combination of sets of the form
{x ∈ Kn : p(x) = 0} and {x ∈ Kn : q(x) > 0},
where p, q ∈ K [X1, . . ., Xn]. By quantifier elimination, the definable sets in a real closed field are easily shown to be exactly the semialgebraic sets.
A simple application of this fact is that if A is a semialgebraic subset of  n, then the closure of A is also semialgebraic. Indeed, the closure of A is, by definition, the set
n, then the closure of A is also semialgebraic. Indeed, the closure of A is, by definition, the set

This is a definable set, and hence a semialgebraic set.
Semialgebraic subsets of the real line are particularly simple. For any real polynomial f in one variable, the set {x ∈  : f(x) > 0} is a finite union of open intervals. Therefore, any semialgebraic subset of
: f(x) > 0} is a finite union of open intervals. Therefore, any semialgebraic subset of  is a finite union of points and intervals. This simple fact is the starting point of the modern model-theoretic approach to
is a finite union of points and intervals. This simple fact is the starting point of the modern model-theoretic approach to  . Let
. Let  * be a language extending
* be a language extending  or and let
or and let  * denote the reals considered as an
* denote the reals considered as an  *-structure. For example, below we will be interested in the case where
*-structure. For example, below we will be interested in the case where  * =
* =  exp and
exp and  * =
* =  exp. We say that
exp. We say that  * is o-minimal if every subset of
* is o-minimal if every subset of  definable using
definable using  *-formulas is a finite union of points and intervals. The “o” in “o-minimal” stands for “ordered.”
*-formulas is a finite union of points and intervals. The “o” in “o-minimal” stands for “ordered.”  * is o-minimal if every definable subset of
* is o-minimal if every definable subset of  can be defined using only the ordering.
can be defined using only the ordering.
Pillay and Steinhorn introduced o-minimality, generalizing an earlier idea of van den Dries. It turned out to be a key definition, because although o-minimality is defined in terms of the one-dimensional set  , it has remarkably strong consequences for definable subsets of
, it has remarkably strong consequences for definable subsets of  n when n > 1.
n when n > 1.
To explain this, we inductively define a collection of basic sets called cells as follows.
• A subset X of  is a cell if and only if it is either a point or an interval.
is a cell if and only if it is either a point or an interval.
• If X is a cell in  n and f is a continuous definable function from X to
n and f is a continuous definable function from X to  , then the graph of f (which is a subset of
, then the graph of f (which is a subset of  n+1) is a cell.
n+1) is a cell.
• If X is a cell in  n and f and g are continuous definable functions from X to
n and f and g are continuous definable functions from X to  such that f(x) > g(x) for every x ∈ X, then {(x, y) : x ∈ X and f(x) > y > g(x)} is a cell, as are {(x, y) : x ∈ X and f(x) > y} and {(x, y) : x ∈ X and y > f(x)}.
such that f(x) > g(x) for every x ∈ X, then {(x, y) : x ∈ X and f(x) > y > g(x)} is a cell, as are {(x, y) : x ∈ X and f(x) > y} and {(x, y) : x ∈ X and y > f(x)}.
Cells are topologically simple definable sets that play the role of open intervals in  . It is not hard to see that any cell is homeomorphic to (0, 1)n for some n. Remarkably, all definable sets can be decomposed into cells. The following theorem is a precise version of this statement.
. It is not hard to see that any cell is homeomorphic to (0, 1)n for some n. Remarkably, all definable sets can be decomposed into cells. The following theorem is a precise version of this statement.
Theorem.
(i) If  * is an o-minimal structure, then every definable set × can be partitioned into finitely many disjoint cells.
* is an o-minimal structure, then every definable set × can be partitioned into finitely many disjoint cells.
(ii) If f : X →  is a definable function, then there is a partition of × into finitely many cells such that f is continuous on each cell.
is a definable function, then there is a partition of × into finitely many cells such that f is continuous on each cell.
This is just the beginning. In any o-minimal structure, definable sets have many of the good topological and geometric properties of the semialgebraic sets. For example:
• Any definable set has finitely many connected components.
• Definable bounded sets can be definably triangulated.
• Suppose that X is a definable subset of  n+m. For each a ∈
n+m. For each a ∈  m, let Xa be the “cross-section” {x ∈
m, let Xa be the “cross-section” {x ∈  n : (x, a) ∈ X}. Then there are only finitely many different homeomorphism types for the sets Xa.
n : (x, a) ∈ X}. Then there are only finitely many different homeomorphism types for the sets Xa.
As these results were known for semialgebraic sets, the real interest is in finding new o-minimal structures. The most interesting example is  exp. It is known that
exp. It is known that  exp does not have quantifier elimination in the language
exp does not have quantifier elimination in the language  exp. Wilkie showed that the next best thing is true. We say that
exp. Wilkie showed that the next best thing is true. We say that  n is an exponential variety if it is the zero set of a finite system of exponential terms. For example, the set {(x, y, z) : x = exp(y)2 – z3 ∧ exp(exp(z)) = y – x} is an exponential variety.
n is an exponential variety if it is the zero set of a finite system of exponential terms. For example, the set {(x, y, z) : x = exp(y)2 – z3 ∧ exp(exp(z)) = y – x} is an exponential variety.
Theorem. Every  exp-definable subset of
exp-definable subset of  n is of the form
n is of the form

for some exponential variety V ⊆  n+m.
n+m.
In other words, the definable sets, though not exponential varieties themselves, are projections of exponential varieties, which makes them tractable. Indeed, a theorem from real analytic geometry, due to Khovanskii, states that every exponential variety has a finite number of connected components. Since this property is preserved by projections, it follows that every definable set has a finite number of connected components, and also that every definable subset of the real line is a finite union of points and intervals. Thus  exp is o-minimal and all of the results above about definable sets in o-minimal structures apply.
exp is o-minimal and all of the results above about definable sets in o-minimal structures apply.
Tarski asked if the theory of  exp is decidable. This question remains open, but the answer is known to follow from the following conjecture of Schanuel in transcendental number theory.
exp is decidable. This question remains open, but the answer is known to follow from the following conjecture of Schanuel in transcendental number theory.
Conjecture. Suppose that λ1, . . .,λn are complex numbers that are linearly independent over  . Then the field
. Then the field  (λ1, . . ., λn, eλ1, . . ., eλn) has transcendence degree at least n.
(λ1, . . ., λn, eλ1, . . ., eλn) has transcendence degree at least n.
Macintyre and Wilkie have shown that if Schanuel’s conjecture is true, then the theory of  exp is decidable.
exp is decidable.
6 The Random Graph
Model-theoretic methods give interesting information about random GRAPHS [III.34]. Suppose we construct a graph as follows. The vertex set is the set 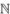 of all natural numbers
of all natural numbers 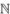 . To decide whether we will have an edge between x and y (with x ≠ y) we flip a coin, putting an edge there if and only if we get heads. Although these constructions are random, we will show below that, with probability 1, any two such graphs are isomorphic.
. To decide whether we will have an edge between x and y (with x ≠ y) we flip a coin, putting an edge there if and only if we get heads. Although these constructions are random, we will show below that, with probability 1, any two such graphs are isomorphic.
The proof depends on the following extension property. Let A and B be disjoint finite subsets of 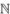 , and suppose that they have sizes n and m, respectively. We would like to find a vertex x ∈
, and suppose that they have sizes n and m, respectively. We would like to find a vertex x ∈ 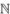 that is joined to every element of A and to no element of B. Now for any particular x, the probability that it does not have the desired property is
that is joined to every element of A and to no element of B. Now for any particular x, the probability that it does not have the desired property is  = 1 - 2-(n+m). Therefore, if we look at N different vertices, the probability that none of them has the desired property is
= 1 - 2-(n+m). Therefore, if we look at N different vertices, the probability that none of them has the desired property is  N. Since this converges to zero with N, the probability that at least one x ∈
N. Since this converges to zero with N, the probability that at least one x ∈ 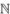 has the property is 1. Moreover, since there are only countably many disjoint pairs (A, B) of finite sets, with probability 1 it is the case that for every such pair (A, B) one can find a vertex x that is joined to every vertex in A and to no vertex in B.
has the property is 1. Moreover, since there are only countably many disjoint pairs (A, B) of finite sets, with probability 1 it is the case that for every such pair (A, B) one can find a vertex x that is joined to every vertex in A and to no vertex in B.
We can formalize this observation in a model-theoretic way. Let  g =
g =  (∼), where “∼” is a binary relation symbol (which we read as “is joined to”). We let T be the
(∼), where “∼” is a binary relation symbol (which we read as “is joined to”). We let T be the  g-theory:
g-theory:
(i) ∀x∀y x ∼ y → y ∼ x
(ii) ∀x ¬(x ∼ x);
(iii) Φn,m for n, m  0.
0.
Here Φn,m is the sentence
∀xl . . . ∀xn ∀y1 . . . ∀ym
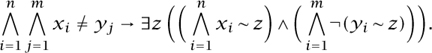
The first two sentences tell us that the relation “∼” defines a graph, and for each pair (n, m) the sentence Φn,m tells us that the extension property holds for all pairs of disjoint sets A and B with A of size n and B of size m. Thus, a model of T is a graph for which the extension property holds for any pair of disjoint finite sets of vertices.
The argument above shows that with probability 1 the random graphs we constructed are models of T. Now let us see why they are isomorphic (again with probability 1). This will be an immediate consequence of the following theorem.
Theorem. If G1 and G2 are any two countable models of T, then G1 is isomorphic to G2.
Recall that an isomorphism between G1 and G2 means a bijection f from the vertex set of G1 to the vertex set of G2 such that x is joined to y in G1 if and only if f(x) is joined to f(y) in G2. The proof, which we shall now sketch, is a “back-and-forth” argument that gradually builds up an isomorphism between G1 and G2. First, let a0, a1, . . . be an enumeration of the vertices of G1 and let b0, b1, . . . be an enumeration of the vertices of G2. Let us set f (a0) to be b0. Next, we choose an image for a1: if a1 is joined to a0 then we need to find some vertex that is joined to b0 and if a1 is not joined to a0 then we need to find a vertex that is not joined to b0. Either way, we can do it because G is a model of T, so it satisfies the extension property. (The particular cases we use here are Φ1,0 and Φ0,1.)
It is tempting to continue finding images for a2, a3, and so on, in each case using the extension property to make sure that the images are joined to each other if and only if the original vertices are. The trouble with this is that we may not end up with a bijection, since for any particular bj there is no guarantee that we will ever choose it as the image of some aj. However, we can remedy this by alternately choosing an image for the first bj that does not yet have an image, and a preimage for the first b that does not yet have a preimage. In this way we build the desired isomorphism.
It was not essential to use model theory to prove the above result. However, it has the following very nice model-theoretic consequence.
Corollary. For any  g-sentence
g-sentence  either
either  is true in every model of T or ¬
is true in every model of T or ¬ is true in every model of T. Moreover, there is an algorithm that will tell us which of
is true in every model of T. Moreover, there is an algorithm that will tell us which of  or ¬
or ¬ is true in every model of T.
is true in every model of T.
To prove this, one first applies a slight strengthening of the compactness theorem, which allows one to conclude that if the result is false then there are countable models G1 and G2 of T such that  is true in G1 and ¬
is true in G1 and ¬ is true in G2. But this shows that G1 and G2 are not isomorphic, and therefore directly contradicts the previous theorem.
is true in G2. But this shows that G1 and G2 are not isomorphic, and therefore directly contradicts the previous theorem.
To decide which of  or ¬
or ¬ is true in every model of T, one searches through all possible proofs from the sentences of T. By the completeness theorem, one or other of the statements has a proof, so we will eventually find either a proof of
is true in every model of T, one searches through all possible proofs from the sentences of T. By the completeness theorem, one or other of the statements has a proof, so we will eventually find either a proof of  or a proof of ¬
or a proof of ¬ . At that point we will know which of
. At that point we will know which of  and ¬
and ¬ is true in every model of T.
is true in every model of T.
The theory T also gives us information about random finite graphs. Let  N be the set of all graphs with vertices {1, 2, . . ., N}. We consider the probability measure
N be the set of all graphs with vertices {1, 2, . . ., N}. We consider the probability measure  N on in which we make all graphs equally likely. This is the same as constructing a random graph on N vertices, where for each i and j we toss an unbiased coin in order to decide whether i is joined to j. For any
N on in which we make all graphs equally likely. This is the same as constructing a random graph on N vertices, where for each i and j we toss an unbiased coin in order to decide whether i is joined to j. For any  g sentence
g sentence  , let us write
, let us write  N (
N ( ) for the probability that a random graph on N vertices satisfies
) for the probability that a random graph on N vertices satisfies  .
.
An easy variant of the argument for infinite graphs shows that for each extension axiom Φn,m, the probability  N (
N ( n,m) tends to 1. Therefore, for any fixed M, if N is sufficiently large, then with very high probability a random graph on N vertices satisfies all the axioms Φn,m with n, m
n,m) tends to 1. Therefore, for any fixed M, if N is sufficiently large, then with very high probability a random graph on N vertices satisfies all the axioms Φn,m with n, m 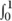 M.
M.
This observation allows us to use the theory T to get a good understanding of the asymptotic properties of random graphs. The following result is called a zero-one law.
Theorem. Given any  g-sentence
g-sentence  , the probability
, the probability  N (
N ( ) either tends to 0 or tends to 1 as N → ∞. Moreover, T axiomatizes the set of statements
) either tends to 0 or tends to 1 as N → ∞. Moreover, T axiomatizes the set of statements  such that the limit is 1, called the almost sure theory of graphs, which is a decidable theory.
such that the limit is 1, called the almost sure theory of graphs, which is a decidable theory.
This follows from our previous results. We saw earlier that either  is true in every model of T or ¬
is true in every model of T or ¬ is true in every model of T. In the first case, by the completeness theorem there must be a proof of Φ from T. Since proofs are finite, this proof can use only finitely many of the statements Φn,m. Therefore, there exists some M such that if G
is true in every model of T. In the first case, by the completeness theorem there must be a proof of Φ from T. Since proofs are finite, this proof can use only finitely many of the statements Φn,m. Therefore, there exists some M such that if G 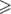 ΦM,M, then G
ΦM,M, then G 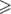
 . But if G is a random graph on N vertices, then the probability that G
. But if G is a random graph on N vertices, then the probability that G 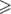
 tends to 1, and therefore the probability
tends to 1, and therefore the probability  N (
N ( ) that G
) that G 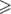 tends to 1 as well. The same argument holds if ¬
tends to 1 as well. The same argument holds if ¬ is true in every model of T and shows that
is true in every model of T and shows that  N(¬
N(¬ ) tends to 1, which implies that
) tends to 1, which implies that  N(
N( ) tends to 0.
) tends to 0.
Note the following interesting consequence of this result. It is not hard to prove that the probability that a random graph contains at least 
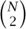 edges converges to
edges converges to  as N tends to infinity. Combining this simple observation with the theorem we can deduce that the property “contains at least as many edges as nonedges” cannot be expressed by a first-order formula in
as N tends to infinity. Combining this simple observation with the theorem we can deduce that the property “contains at least as many edges as nonedges” cannot be expressed by a first-order formula in  g. This is a purely syntactic result, but to prove it we made essential use of model theory.
g. This is a purely syntactic result, but to prove it we made essential use of model theory.
Further Reading
Shoenfield (2001) is an excellent introduction to logic including the completeness and incompleteness theorems, basic computability theory, and elementary model theory.
The examples described here give only a small part of the flavor for modern model theory. Hodges (1993), Marker (2002), and Poizat (2000) are comprehensive introductions. Marker et al. (1995) contains several introductory articles on the model theory of fields.
In addition to providing tools for analyzing definability in particular structures, a major goal in model theory is proving structure theorems for wide classes of mathematical structures. A key feature is the development by Shelah of notions of dependence generalizing linear dependence in vector spaces and algebraic dependence in fields. Led by Hrushovski and Zilber, model theorists have studied the geometry of dependence and found that frequently it can be used to detect hidden algebraic structure.
In recent years, abstract model theory has found interesting applications in classical mathematics. Hrushovski used these ideas to give a model-theoretic proof of the Mordell–Lang conjecture for function fields in Diophantine geometry. Bouscaren (1998) is an excellent collection of survey articles leading up to Hrushovski’s proof.
Bouscaren, E., ed. 1998. Model Theory and Algebraic Geometry. An Introduction to E. Hrushovski’s Proof of the Geometric Mordell–Lang Conjecture. New York: Springer.
Hodges, W. 1993. Model Theory. Encyclopedia of Mathematics and Its Applications, volume 42. Cambridge: Cambridge University Press.
Marker, D. 2002. Model Theory: An Introduction. New York: Springer.
Marker, D., M. Messmer, and A. Pillay. 1995. Model Theory of Fields. New York: Springer.
Poizat, B. 2000. A Course in Model Theory. An Introduction to Contemporary Mathematical Logic. New York: Springer.
Shoenfield, J. 2001. Mathematical Logic. Natick, MA: A. K. Peters.
 and ψ are formulas, then ¬
and ψ are formulas, then ¬ ,
,  ∨ ψ,
∨ ψ,  ∧ ψ,
∧ ψ,  → ψ, and
→ ψ, and  ↔ ψ are all formulas. In general, if
↔ ψ are all formulas. In general, if  is built out of smaller formulas
is built out of smaller formulas  1, . . . ,
1, . . . ,  n using logical connectives (and parentheses), then we call
n using logical connectives (and parentheses), then we call  a Boolean combination of
a Boolean combination of  1, . . . ,
1, . . . ,  n. Another important way to modify a formula is quantification: if
n. Another important way to modify a formula is quantification: if  (x) is a formula involving a free variable x, then ∀x
(x) is a formula involving a free variable x, then ∀x (x) and ∃x
(x) and ∃x (x) are both formulas.
(x) are both formulas. exp. Formulas (i) and (ii) are true in
exp. Formulas (i) and (ii) are true in  is an
is an  exp-sentence, then
exp-sentence, then 
 , +, ·, 0, 1): that is, the integers, with addition, multiplication, 0, and 1. The language used to describe this structure is the language of rings,
, +, ·, 0, 1): that is, the integers, with addition, multiplication, 0, and 1. The language used to describe this structure is the language of rings,  0 can be defined by the formula
0 can be defined by the formula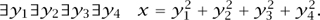
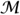 in which all the sentences of T, suitably interpreted, are true. For instance, the structure was a model for the formulas (i) and (ii) of the language
in which all the sentences of T, suitably interpreted, are true. For instance, the structure was a model for the formulas (i) and (ii) of the language 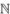 , +, ·, 0, 1), or the complex field, and a language
, +, ·, 0, 1), or the complex field, and a language 

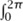 ϕ.
ϕ.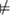 ϕ, our program above will go on searching forever, so it will never tell us that there is no proof of ϕ. We say that an
ϕ, our program above will go on searching forever, so it will never tell us that there is no proof of ϕ. We say that an 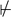 ψ.
ψ.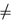 0, 1 + 1 + 1
0, 1 + 1 + 1  4ac. Therefore,
4ac. Therefore,  ϕ(a, b, c) if and only if
ϕ(a, b, c) if and only if
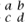 is invertible. However, by the DETERMINANT [III.15] test, we know that, for any field F, F
is invertible. However, by the DETERMINANT [III.15] test, we know that, for any field F, F 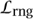 -formula ϕ there is a quantifier-free formula ψ such that ϕ is equivalent to ψ in every algebraically closed field.
-formula ϕ there is a quantifier-free formula ψ such that ϕ is equivalent to ψ in every algebraically closed field.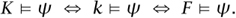
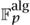 , the algebraic closure of the p-element field. (It can be shown that any field F is contained in an algebraically closed field. Roughly speaking, the algebraic closure of F is the smallest algebraically closed field that contains F.) Suppose, then, that some ϕd fails for
, the algebraic closure of the p-element field. (It can be shown that any field F is contained in an algebraically closed field. Roughly speaking, the algebraic closure of F is the smallest algebraically closed field that contains F.) Suppose, then, that some ϕd fails for 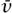 for the n-tuple (v1, . . ., vn).)
for the n-tuple (v1, . . ., vn).)
 or be the language of ordered rings, which is the language of rings with the addition of the symbol “<” for an ordering. Which
or be the language of ordered rings, which is the language of rings with the addition of the symbol “<” for an ordering. Which 
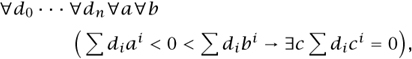
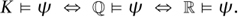


 . Then the field
. Then the field  = 1 - 2-(n+m). Therefore, if we look at N different vertices, the probability that none of them has the desired property is
= 1 - 2-(n+m). Therefore, if we look at N different vertices, the probability that none of them has the desired property is  0.
0.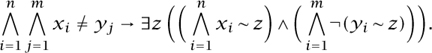
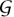 N be the set of all graphs with vertices {1, 2, . . ., N}. We consider the probability measure
N be the set of all graphs with vertices {1, 2, . . ., N}. We consider the probability measure 
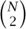 edges converges to
edges converges to