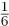 , then the ABC conjecture gives us a constant K such that c cannot be more than K(c3/r)7/6 = Kc7/2r. If r ≥ 4 then the power 7/2r is less than 1, so the Fermat equation can have at most finitely many solutions with x, y, and z coprime.
, then the ABC conjecture gives us a constant K such that c cannot be more than K(c3/r)7/6 = Kc7/2r. If r ≥ 4 then the power 7/2r is less than 1, so the Fermat equation can have at most finitely many solutions with x, y, and z coprime.The ABC conjecture, proposed by Masser and Oesterlé in 1985, is a bold and very general conjecture in number theory with a wide range of important consequences. The rough idea of the conjecture is that it is impossible for one number to be the sum of two others if all three numbers have many repeated prime factors and no two have a prime factor in common (which would then have to be shared by the third).
More precisely, one defines the radical of a positive integer n to be the product of all primes that divide n, with each distinct prime included just once. For instance, 3960 = 23 × 32 × 5 × 11, so its radical is 2 × 3 × 5 × 11 = 330. Let us write rad(n) for the radical of n. The ABC conjecture asserts that for every positive real number ∈ there is a constant K∈ such that if a, b, and c are coprime integers and a + b = c, then c < K∈ rad(abc)1 +∈.
To get a feel for the meaning of this conjecture, consider the Fermat equation xr + yr = zr. If three positive integers x, y, and z solve the equation, then we can divide through by any common factors they might have and obtain a solution for which x, y, and z, and hence their rth powers, are coprime. Set a = xr, b = yr, and c = zr. Then
rad(abc) = rad(xyz) ≤ xyz = (abc)1/r ≤ c3/r,
where the last inequality follows from the fact that c is greater than both a or b. If we set ∈ to be 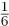 , then the ABC conjecture gives us a constant K such that c cannot be more than K(c3/r)7/6 = Kc7/2r. If r ≥ 4 then the power 7/2r is less than 1, so the Fermat equation can have at most finitely many solutions with x, y, and z coprime.
, then the ABC conjecture gives us a constant K such that c cannot be more than K(c3/r)7/6 = Kc7/2r. If r ≥ 4 then the power 7/2r is less than 1, so the Fermat equation can have at most finitely many solutions with x, y, and z coprime.
It is clear that this is just one of a huge number of consequences of a similar kind. For instance, we could deduce that there are only finitely many solutions of the equation 2r + 3s = x2, since the radical of 2r3sx2 is at most 6x, which is considerably smaller than x2. But the ABC conjecture has other consequences that are less obvious, and more important, than this one. For instance, Bombieri has shown that the ABC conjecture implies ROTH’S THEOREM [V.22], Elkies has shown that it implies the MORDELL CONJECTURE [V.29], and Granville and Stark have shown that a strengthening of the ABC conjecture implies the nonexistence of Siegel zeros (these are defined in ANALYTIC NUMBER THEORY [IV.2]). It is also equivalent to strong forms, as yet unproven, of a famous theorem of Baker in transcendence theory, and of the theorem of Wiles about MODULAR FORMS [III.59] that implies Fermat’s last theorem.
The ABC conjecture is discussed further in COMPUTATIONAL NUMBER THEORY [IV.3].