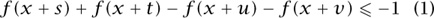
The Banach–Tarski paradox states that there is a way of decomposing a three-dimensional ball of unit radius into a finite number of disjoint pieces, then reassembling the pieces to form two balls of unit radius, where “reassembling” means that the pieces are translated and rotated and that they end up still disjoint.
Such a result seems impossible at first sight, and indeed it contradicts the naive assumption that one can consistently assign a finite volume to every bounded set. In other words, it shows that one cannot assign volumes to all bounded sets in such a way that these volumes are unaffected by translation and rotation, that the volume of a union of two disjoint sets is the sum of the volumes of the two sets, and that the volume of the unit ball is greater than zero. However, if we drop this naive assumption, then the paradox disappears. Since there is no genuine paradox, we shall refer to the Banach–Tarski construction.
The Banach–Tarski construction is a descendant of an older construction due to Vitali, which concerns area rather than volume. Let us write lθ for the line segment in ℝ2 that is given in polar coordinates by
lθ = {(r, θ):0 < r ≤ 1}.
Note that the union of all such segments is the punctured unit disk D* (that is to say, the unit disk with the origin removed). We say that lθ and lϕ belong to the same equivalence class if θ - ϕ is a rational multiple of π, and we consider a set E that is the union of a set of lθ containing exactly one representative from each equivalence class.
The rationals are COUNTABLE [III.11], so we can enumerate the rationals x with 0 ≤ x < 1 as a sequence x1, x2, . . . . If we write
En = {lθ+2πxn: lθ ∈ E},
then each En is obtained from E by a rotation about the origin (through an angle 2πxn), the En are disjoint (as E contains only one representative from each equivalence class), and the union of the En is D* (as E contains a representative from each equivalence class).
Now take D* and split it into the set F consisting of the union of the sets E2n and the set G consisting of the union of the sets E2n+1. Each E2n can be rotated to E, and the union of the En gives us D*. Similarly, each E2n+1 can be rotated to En, and the union of the En gives us D* again. Thus the punctured unit disk can be split into a countable set of disjoint pieces (all obtained by rotation of one particular set) which can be rotated and translated to form disjoint sets whose union is two copies of D*.
Vitali’s construction makes use of THE AXIOM OF CHOICE [III.1] (because we chose one representative from each equivalence class), and the same is true for the Banach–Tarski construction. Solovay showed that if we reject the axiom of choice, then there are MODELS OF SET THEORY [IV.22 §3] in which it is possible to assign a volume to all bounded sets in ℝ3 in a consistent way. However, most mathematicians would agree that the natural moral to draw from our discussion is that when we define volume we should consider only a restricted collection of sets.
The Banach–Tarski construction is also closely related to our final example, which requires a little group theory. To introduce this example of bad behavior, we first consider an example of good behavior. Suppose that f : ℝ → ℝ is a reasonable function with f (x) ≥ 0 and f (x + 1) f(x) for all x (thus, f is nonnegative and periodic with period 1). Suppose that there existed real numbers s, t, u, v such that
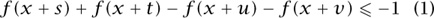
for all x. Since  f (x + w) dx =
f (x + w) dx =  f (x) dx for all w, integrating both sides of (1) from 0 to 1 would give
f (x) dx for all w, integrating both sides of (1) from 0 to 1 would give

which is impossible. Thus (1) cannot hold.
Now consider the FREE GROUP [IV.10 §2] G generated by a and b (that is to say, the group generated by a and b where no nontrivial relations hold between a and b). Every element of G can be written in shortest form as the product of a sequence, each term of which is a, a-1, b, or b-1. Define F(x) = 1 if x = e or the shortest form of x ends with a or a-1, and set F(x) = 0 otherwise. We see that F(x) ≥ 0 for all x ∈ G, and the reader can check, by going through cases, that
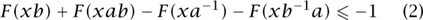
for all x ∈ G. The averaging argument that enabled us to show that (1) was false for ℝ must fail for G since (2) is, in fact, true. If there is no averaging argument, then there can be no appropriate universal integral and no appropriate universal “volume” in G.
This example bears a clear family resemblance to the “paradoxes” discussed earlier. If we consider the group SO(3) of rotations in three dimensions, then (unless specific conditions hold) there is no nontrivial group relation between two generally chosen rotations A and B about two generally chosen axes. Thus SO(3) contains a copy of the group G considered in the previous paragraph. The Banach–Tarski construction is a modification of a construction of Hausdorff that exploits this fact.
There is a beautiful account of all these matters in The Banach–Tarski Paradox by Stan Wagon (Cambridge University Press, Cambridge, UK, 1993).